Нейронные сети и dataset IRIS
С чего всё началось
Я являюсь учеником 4 курса по специальности «информационные технологии» и обучаюсь в институте под названием ЯГТУ.
На последнем семестре у нас появился предмет под названием «Интеллектуальные системы и технологии», в связи с чем я заинтересовался данной темой.
Эта работа будет посвящена анализу данных на основе датасета IRIS, а также с использованием таких библиотек как tensorflow, sklearn, ctgan. Естеcnвенно писать код мы будем на Python.
Немного о нейронных сетях
Думаю сильно углубляться в теорию нейронных сетей в данной статье не имеет смысла, информации об этом достаточно в других статьях на этом форуме, или же просто в интернете. Поэтому сосредоточимся на модели сети которую будем использовать.
В данной статье мы будем использовать последовательную нейронную сеть Squental из билиотеки tensorflow.
Sequental модель подходит для простого стека слоев , где каждый слой имеет ровно один входной и один выходной тензор.
В контексте нейронных сетей тензор обычно представляет собой многомерный массив чисел, который используется для хранения и обработки данных. Нейронные сети оперируют тензорами на различных этапах обучения и применения, таких как входные данные (например, изображения, звуки, тексты), веса и смещения (parameters), а также промежуточные активации в различных слоях сети.
Важно отметить, что тензоры в нейронных сетях могут иметь различные размерности. Например:
Тензор ранга 0 — скаляр (например, одно число).
Тензор ранга 1 — вектор (например, одномерный массив чисел).
Тензор ранга 2 — матрица (двумерный массив чисел).
Тензоры более высоких рангов — многомерные массивы чисел.
В процессе обучения нейронных сетей тензоры передаются через слои сети, на которых выполняются математические операции, такие как умножение матриц, применение активаций и т. д. Тензоры также используются для представления градиентов, которые используются для обновления весов в процессе обучения методом обратного распространения ошибки.
Нейрон — базовая единица нейронной сети. У каждого нейрона есть определённое количество входов, куда поступают сигналы, которые суммируются с учётом значимости (веса) каждого входа. Далее сигналы поступают на входы других нейронов. Вес каждого такого «узла» может быть как положительным, так и отрицательным. Например, если у нейрона есть четыре входа, то у него есть и четыре весовых значения, которые можно регулировать независимо друг от друга.
Модель нашей сети будет иметь примерно такой вид:
На схеме ниже нейроны представлены синими точками, связи серыми линиями.

Посмотрев на схему можно увидеть, что у нас есть 2 нейрона на входном слое, 10 на 2, 8 на 3, и 3 нейрона на 4. Параметры сети мы будем подбирать исходя из полученной точности предсказания при тестах. Эта нейросеть является полносвязной, т.е. каждый нейрон слоя, связан со всеми нейронами предыдущего слоя. Такие слои имеют название Dense.
Мы будем использовать именно такую модель, так как она эффективна при работе с данными, где важна каждая особенность, независимо от её местоположения во входных данных.
Анализ данных
Для начала загрузим все необходимые библиотеки, чтобы в дальнейшем на это не отвлекаться.
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn import metrics
from pandas import DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
from sklearn.metrics import confusion_matrix, silhouette_score
from sklearn.model_selection import train_test_split
from sklearn.linear_model import SGDClassifier
from ctgan import CTGAN
from sklearn.model_selection import GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import adjusted_rand_score, adjusted_mutual_info_scoreИтак начнём работу с данными. Для этого загружаем сам датасет.
iris = datasets.load_iris()В этом датасете содержится информация о 3 различных видах ирисов и их параметров, всего 150 цветов, по 50 примеров на цветок соответственно.
Виды цветков:
Iris setosa
Iris versicolor
Iris virginica
Характеристики цветков:
Длина чашелистика (sepal length) в сантиметрах.
Ширина чашелистика (sepal width) в сантиметрах.
Длина лепестка (petal length) в сантиметрах.
Ширина лепестка (petal width) в сантиметрах.
Проведя исследования на стандартном наборе параметров, я пришёл к выводу что данных недостаточно для хорошего обучения нейросети, поэтому мы сгенерируем синтетические данные для масштабирования исследования.
Для этого будем использовать библиотеку CTGAN
Мы берём отдельно данные по каждому виду цветка, генерируем значения в количестве 2000 штук для каждого цветка, соединяем в один массив и заменяем изначальные данные.
iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
iris_df['species'] = iris.target_names[iris.target]
# Выбор данных для каждого типа ириса
setosa = iris_df[iris_df['species'] == 'setosa']
versicolor = iris_df[iris_df['species'] == 'versicolor']
virginica = iris_df[iris_df['species'] == 'virginica']
#Создание модели нейросети
ctgan = CTGAN(
epochs=50, # Эпохи обучения, тут главное не переобучить нейросеть
)
ColSamples = 2000
# Обучение модели на основе данных о setosa. Не забудем что должны убрать последнюю
#колонку, т.к. в ней содержится просто название цветка.
ctgan.fit(setosa.iloc[:,:-1])
# Генерация синтетических данных
setosa = ctgan.sample(ColSamples)
ctgan.fit(versicolor.iloc[:,:-1])
# Генерация синтетических данных
versicolor = ctgan.sample(ColSamples)
ctgan.fit(virginica.iloc[:,:-1])
# Генерация синтетических данных
virginica = ctgan.sample(ColSamples)
iris.data = np.concatenate((setosa, versicolor, virginica))Далее мы также должны создать массив из такого же количества 0, 1 и 2. Так как по этим маркером будет определяться к какому виду принадлежат те или иные значения.
# Создание массива с ColSamples нулями
zeros = np.zeros(ColSamples, dtype=int)
# Создание массива с ColSamples единицами
ones = np.ones(ColSamples, dtype=int)
# Создание массива с ColSamples двойками
twos = np.full(ColSamples, 2, dtype=int)
# Объединение массивов в один
new_data = np.concatenate((zeros, ones, twos))
# Объединение существующего датасета с новыми данными
iris.target = new_data
# На всякий случай отсортируем
iris.target = np.sort(iris.target)Далее создаём макет, с которым и будем работать в дальнейшем
iris_frame = DataFrame(iris.data)
# Делаем имена колонок такие же, как имена переменных:
iris_frame.columns = iris.feature_names
# Добавляем столбец с целевой переменной:
iris_frame['target'] = iris.target
# Для наглядности добавляем столбец с сортами:
iris_frame['name'] = iris_frame.target.apply(lambda x: iris.target_names[x])
# Смотрим, что получилось:
print(iris_frame)Выведем график для оценки распределения данных
plt.figure(figsize=(20, 24))
plot_number = 0
for feature_name in iris['feature_names']:
for target_name in iris['target_names']:
plot_number += 1
plt.subplot(4, 3, plot_number)
plt.hist(iris_frame[iris_frame.name == target_name][feature_name])
plt.title(target_name)
plt.xlabel('cm')
plt.ylabel(feature_name[:-4])
plt.show()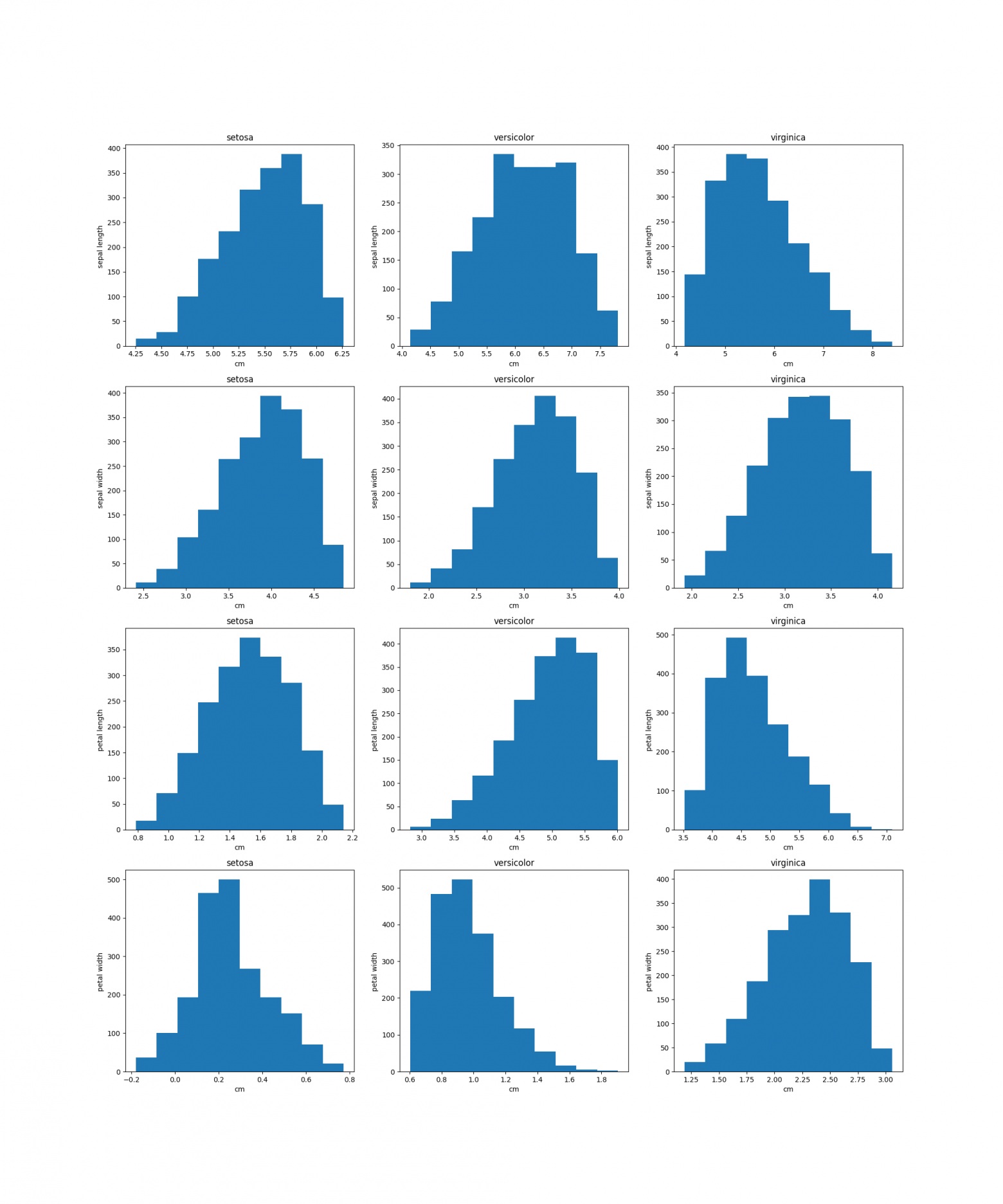
Пока что-либо сказать сложно, но можно заметить, что распределение у некторых значений похоже на нормальное.
Далее для более наглядного результата построим таблицу зависимостей
import seaborn as sns
sns.pairplot(iris_frame[['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)','name']], hue='name')
plt.show()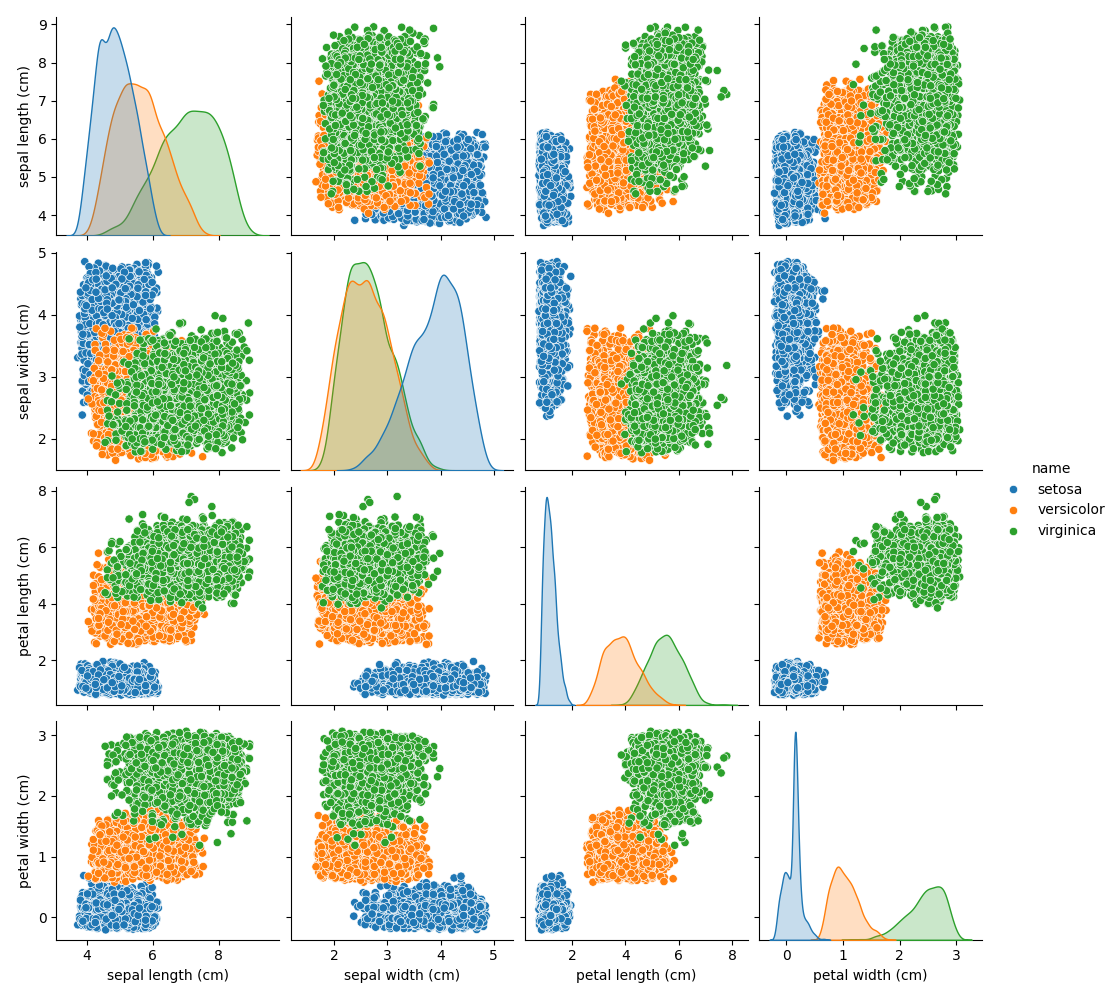
График зависимостей
По этому графику мы точно можем сказать что значения petal length и petal width имеют очень хорошую корреляцию и их распределение похоже на нормальное. А также можно заметить, что кластеризация этих значений явно выражена что также немаловажно при обучении модели. Поэтому принимаем решение работать именно с этими значениям, чтобы в конечном итоге получить хороший результат.
Давайте убедимся в верности суждений графически
corr = iris_frame[['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)']].corr()
mask = np.zeros_like(corr)
mask[np.triu_indices_from(mask)] = True
with sns.axes_style("white"):
ax = sns.heatmap(corr, mask=mask, square=True, cbar=False, annot=True, linewidths=.5)
plt.show()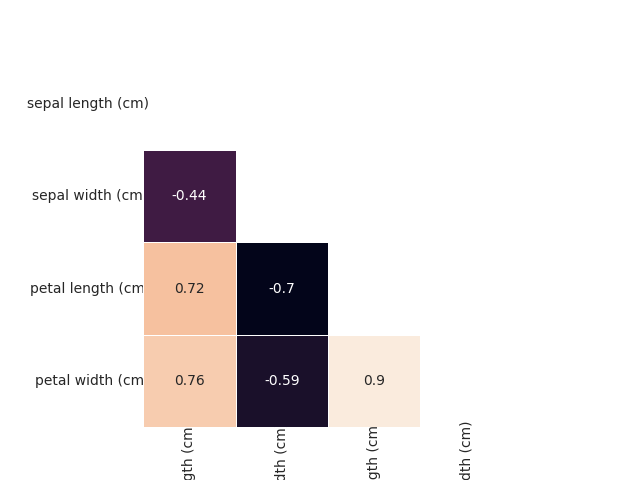
Видим что коэффициент корреляции составляет 0.9 у petal length и petal width.
Отмечу, что работаем мы с синтетическими данными, поэтому каждый раз набор значений у нас будет разный, но за все прогоны этот коэффициент всегда оставался самым большим.
Оценивать много это или мало можно примерно по этим значениям:
До 0,2 — очень слабая корреляция
До 0,5 — слабая
До 0,7 — средняя
До 0,9 — высокая
Больше 0,9 — очень высокая
Разбиваем данные для работы с моделью нейросети
train_data, test_data, train_labels, test_labels = train_test_split(
iris_frame[['petal length (cm)', 'petal width (cm)']],
iris_frame[['target']],
test_size=0.3, #Это значение влияет на то какое количество данных пойдёт на
# обучение модели, а какое на тестирование. соответсвенно на обучение 0.7 всех
# данных, а 0.3 на тестирование, считаю это отношение оптимальным в этом случае
random_state=0
)Строим линию регрессии для наших данных
fit_output = stats.linregress(iris_frame[['petal length (cm)','petal width (cm)']])
slope, intercept, r_value, p_value, slope_std_error = fit_output
print(slope, intercept, r_value, p_value, slope_std_error)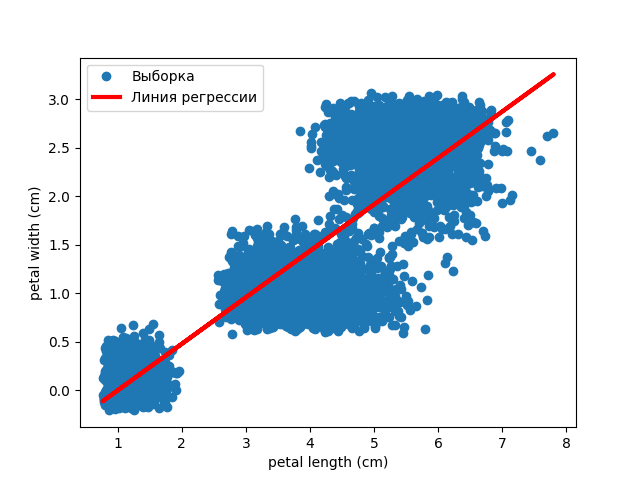
Она минимизирует сумму квадратов расстояний между этой линией и каждой точкой данных. Таким образом, линия регрессии может использоваться для предсказания значения зависимой переменной для заданных значений независимой переменной. Т.е буквально показывает что при длине листа 2 его ширина будет равна 0.5
Видим, что для такого объёма данных, они достаточно неплохо структурированы, и линия регрессии повторяет общую картину распределения точек.
Думаю рассматривать тут SGDClassifier и методы Kmeans, не будем, не очень они подходят для анализа такого объём данных, а результаты оставляют желать лучшего, поэтому приступим к самому интересному.
Создание и обучение нейросети
Оно происходит следующим образом, в датасете каждого набора параметров которые относятся к одному ирису, также относится 0, 1 или 2
Соответственно у нас для:
Iris setosa — 0
Iris versicolor — 1
Iris virginica — 2
И обучение и предсказание происходит следующим образом: алгоритм понимает какие значения относятся к 0, какие к 1, а какие к 2 и при предсказании на выходе мы получаем обычный массив из этих чисел:
[2 1 0 2 0 2 0 1 1 1 1 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0 2 1 1 2 0 2 0 0]
На входе: [2 1 0 2 0 2 0 1 1 1 2 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0 1 1 1 2 0 2 0 0] +
параметры цветка:
[[-0.18295039 -0.29318114]
[ 0.93066067 0.7372463 ]
[ 1.04202177 1.63887031]
[ 0.6522579 0.35083601]
[ 1.09770233 0.7372463 ]
[ 0.03977182 -0.16437771]
[ 1.26474398 1.38126345]
[ 0.48521625 0.47963944]]
Создание модели
#Создаём модель нейросети, задаём количество нейронов и т.п.
model = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation='relu', input_shape=(2,))
# первый слой содержит 64 нейрона, а входной input_shape 2(по количеству входных значений)
tf.keras.layers.Dropout(0.1),
# Dropout - это метод регуляризации, который случайным образом удаляет некоторые нейроны в процессе обучения.
# Это помогает предотвратить переобучение модели, улучшая ее обобщающую способность.
tf.keras.layers.Dense(32, activation='relu'),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(16, activation='relu'),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(8, activation='relu'),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(3, activation='softmax') # Выходной слой с 3 нейронами (по числу классов) и функцией активации softmax для многоклассовой классификации
])
# Компиляция модели
model.compile(optimizer='adam', # Оптимизатор Adam это метод оптимизации, который сочетает в себе идеи метода
#градиентного спуска с адаптивным шагом обучения и метода адаптивной оценки моментов.
loss='sparse_categorical_crossentropy', # Функция потерь для многоклассовой классификации
metrics=['accuracy']) # Метрика - точность классификации
# Обучение модели на train_data указываем количество эпох(50), главное не переобучить модель
history = model.fit(train_data, train_labels, epochs=50, batch_size=2, validation_split=0.2, verbose=1)
# batch_size=2 Это количество образцов данных, передаваемых модели за один раз перед обновлением весов. Меньшие значения обычно означают
# более стабильное обучение, но могут привести к более длительному времени обучения.
# Оценка модели на test_data
test_loss, test_accuracy = model.evaluate(test_data, test_labels, verbose=1)
print("Test Accuracy:", test_accuracy)
predictions = model.predict(test_data)
# Предсказанные метки классов (индексы классов с наибольшей вероятностью)
predicted_classes = predictions.argmax(axis=-1)
# Вывод предсказанных меток классов
print("Predicted classes:", predicted_classes)Получаем в итоге: Test Accuracy: 0.9988889098167419
Можно сделать вывод что результат просто отличный, т.е. при работе нейросети ошибка будет составлять всего 0.1 процент.
Давайте убедимся в этом построив графики с изначальными значениями, и предсказанными
color_dict = {0: 'red', 1: 'green', 2: 'blue'}
plt.figure(figsize=(12, 6))
# Исходные данные
plt.subplot(1, 2, 1)
for idx, true_label in enumerate(test_labels['target']):
plt.plot(test_data.iloc[idx]['petal length (cm)'], test_data.iloc[idx]['petal width (cm)'], 'o', color=color_dict[true_label])
plt.ylabel('petal width (cm)')
plt.xlabel('petal length (cm)')
plt.title('Тестовые данные для предсказания нейронной сетью')
# Вывод кластеризованных данных
plt.subplot(1, 2, 2)
for idx, pred_label in enumerate(predicted_classes):
plt.plot(test_data.iloc[idx]['petal length (cm)'], test_data.iloc[idx]['petal width (cm)'], 'o', color=color_dict[pred_label])
plt.ylabel('petal width (cm)')
plt.xlabel('petal length (cm)')
plt.title('Предсказанные значения')
plt.show()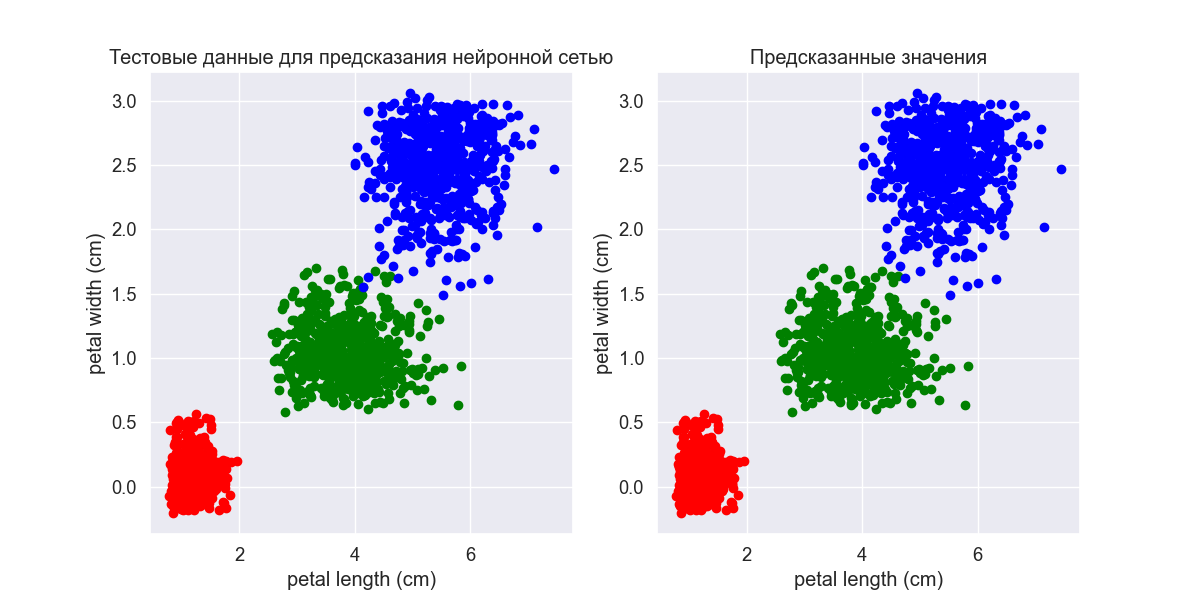
По графику видно что ошибка всего в двух точках при предсказании составляет
2/(6000×0,3) = 0,00111111 или 0,1111%
При такое погрешности можно считать что наша модель является весьма неплохой и имеет место быть.
Также графически мы можем оценить обучение модели
if history is not None:
# Оценка модели на тестовом наборе данных
test_loss, test_accuracy = model.evaluate(test_data, test_labels, verbose=1)
print("Test Accuracy with Dropout:", test_accuracy)
# Построение кривых обучения и валидации
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0, 1])
plt.legend(loc='lower right')
plt.title('Training and Validation Accuracy')
plt.show()
else:
print("Training history is not available.")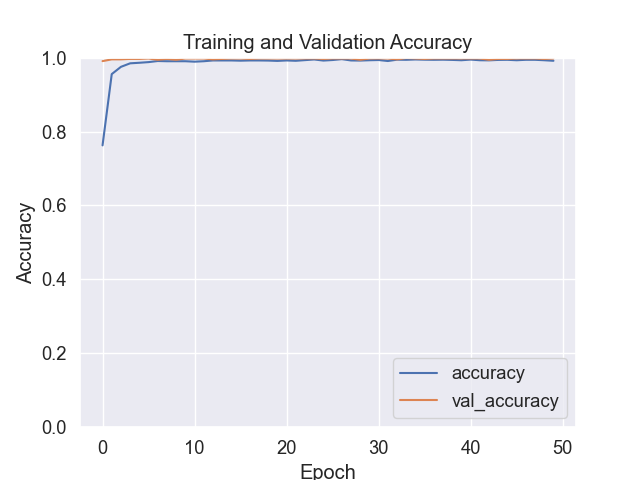
График обучения и валидации представляет собой визуализацию изменения точности (accuracy) модели на протяжении процесса обучения.
Точность на обучающем наборе данных:
Линия accuracy показывает, как меняется точность модели на обучающем наборе данных в течение каждой эпохи обучения. Она отражает, насколько хорошо модель учится на обучающих данных. По мере того как обучение продолжается, точность на обучающем наборе может увеличиваться, но иногда может наблюдаться переобучение, когда точность на обучающем наборе продолжает расти, а точность на валидационном наборе данных начинает уменьшаться.
Точность на валидационном наборе данных:
Линия val_accuracy показывает, как меняется точность модели на валидационном наборе данных в течение каждой эпохи обучения. Валидационный набор данных не используется для обучения модели, но он используется для оценки производительности модели во время обучения. Это помогает определить, насколько хорошо модель обобщает данные, которые она не видела во время обучения. По мере того как обучение продолжается, мы хотим видеть, чтобы точность на валидационном наборе данных увеличивалась, и в идеале приближалась к точности на обучающем наборе данных.
Оригинальный датасет IRIS
Для сравнения покажу что у меня получилось при работе с оригинальным датасетом.
Оригинальные данные имеют следующий вид:
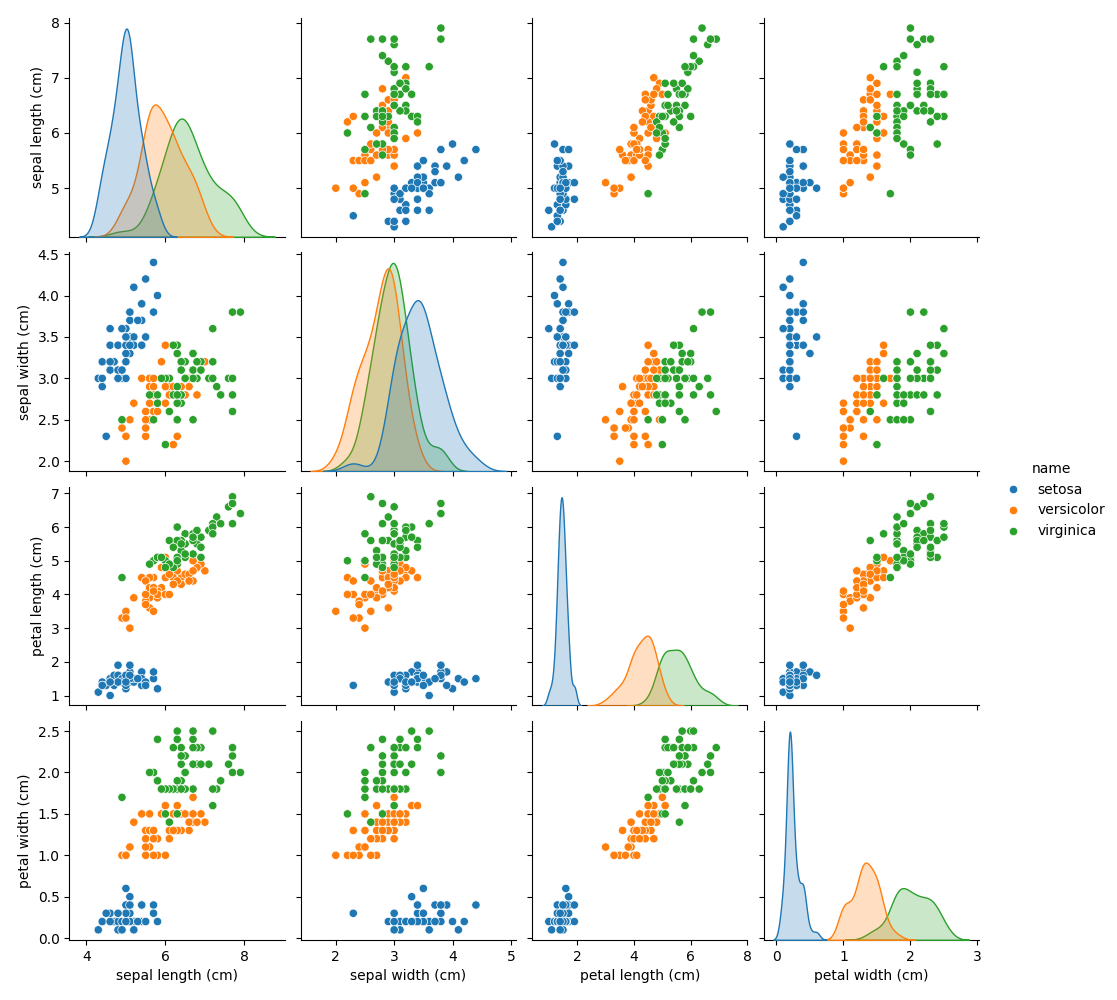
Как видно здесь так же присутствует корреляция между petal length и petal width
Теперь же попробуем тот же способ обучения нейросети, только количество эпох я изменил на 100, в связи с недостаточным количеством данных для обучения
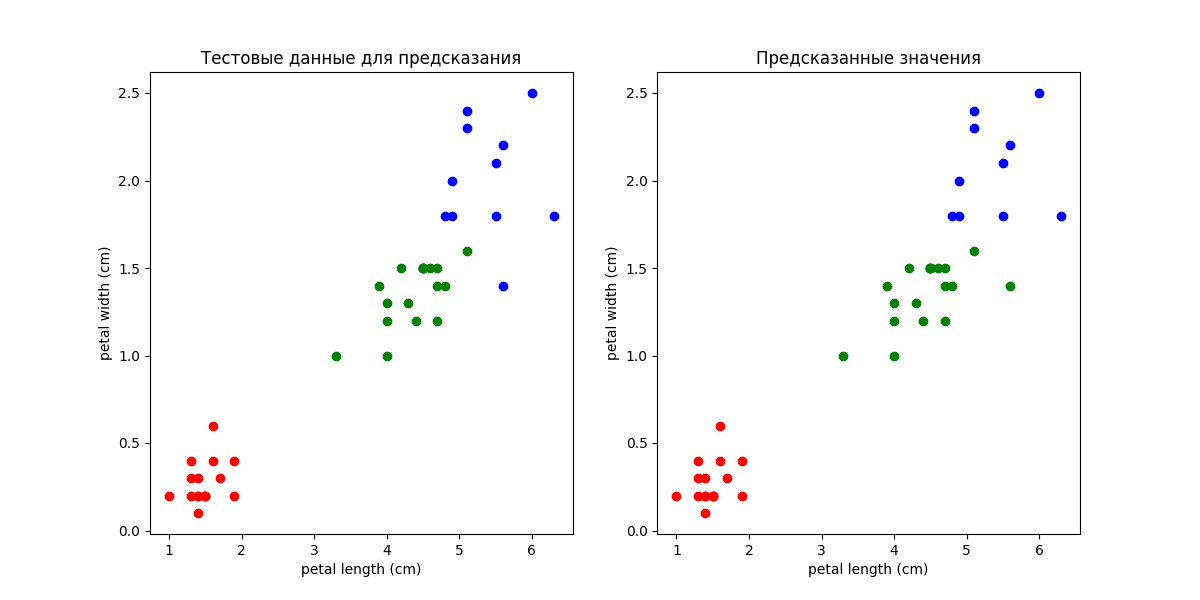
Test Accuracy with Dropout: 0.9777777791023254
Получаем следующие цифры и видим погрешность в 1 точку в данном случае
1/(150×0.3) = 0,0222 или 2,22% что уже является весомым числом при при анализе данных.
Оценка обучения модели графически
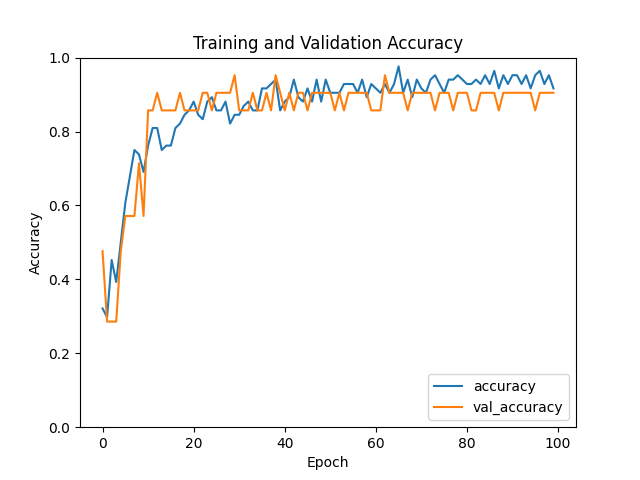
Как видим график уже не такой ровный и аккуратный, что опять же связываю с недостаточным количеством данных. Так же к конце графика мы видим что val_accuracy находится ниже accuracy что явно связано с переобучением модели, попробуем увеличить количество валидационных данных до 0.3 и уменьшить количество эпох до 60
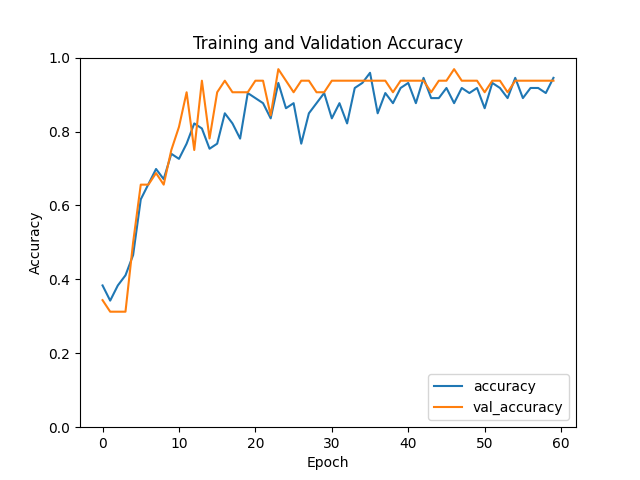
Получаем такой результат, это уже больше походит на правду. При этом график предсказанных значений не изменился, точность получилась следующая 0.9777777791023254. Я провёл пару десятков тестов c разными значениями и моделями, и большей точности с данным набором данных добиться не удалось.
Но в любом случае предсказание значений с помощью нейросети является более точным по сравнению с скажем методом кластеризации KMeans который использует метод k-средних, который заключается в минимизации среднеквадратичного отклонения точек данных от центров кластеров.
model = KMeans(n_clusters=3)#
model.fit(train_data)
model_predictions = model.predict(test_data)
print("Точно при кластеризации KMeans:", metrics.accuracy_score(test_labels, model_predictions))
print("Метрики для KMeans:\n", metrics.classification_report(test_labels, model_predictions))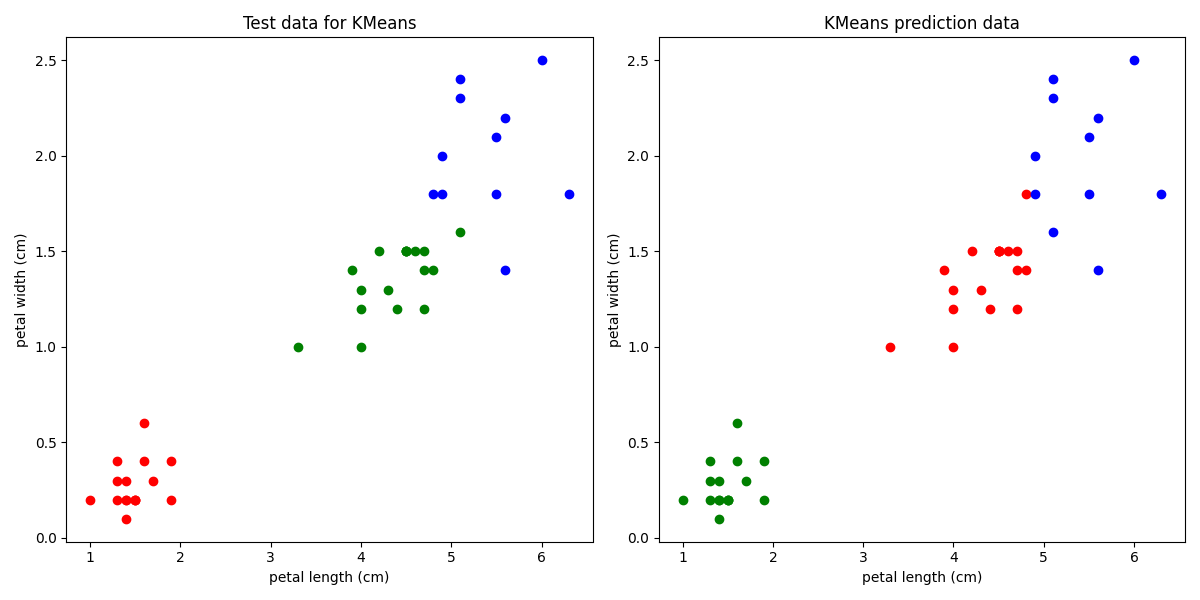
При таком подходе нужно изначально задавать примерные центра кластеров, потому что алгоритм в данном случаем при вычислении алгоритм не понимает где какой именно кластер, и например кластер со значениями 0 может принять значения 1, а 1 принять значения 0 как на рисунке выше. Так как из-за этого точность считалась не корректно то можем на глаз увидеть, что не правильно отобразились 2 точки, следовательно погрешность примерно 2/(150×0.3) = 0.044 = 4.4%
При применении метода KMeans на изменённом мной датасете IRIS точность этого метода сильно ухудшалась и была равна 70–80%
Вывод
Сегодня мы ознакомились с обучением нейронной сети с помощью библиотеки tensorflow. Выяснили какие методы лучше использовать при обработке данных, а так же графически
отобразили, как сильно зависит точность модели от исходных данных, и можем сделать вывод, что чем лучше данные кластеризованы, то тем точнее будет наша модель.
Отмечу что приведение данных к виду, в котором они будут пригодны для работы будет дольше чем построение любой из описанных моделей.
Это моя первая подобная работа, прошу писать любую критику, и что можно доработать.
