Неизвестный библейский алгоритм кластеризации12.03.2025 00:01

Горящий куст двойного отрицания

Времена когда горящий куст мог принести озарение давно прошли. Примитивный опыт уже неможет стать источником открытий. Авсё потому, что он обобщён и впитан вкультуру человечества. Ичтобы подключиться кмудрости предков нужно опереться нафилософию. Вэтой статье мы познакомимся сновым алгоритмом кластеризации и поверхностно затронем некоторые философские категории. Перевернём объективность всубъектность иобратно.

Инструменты кластеризации

Кластеризация — это поиск групп окоторых ничего неизвестно (непутать склассификацией, т. е. сназначением класса элементам). Неизвестность разрешается перебором параметров.

Если известно k количество искомых групп, томожно применить метод k-средних (k-means). Такой алгоритм подбирает центры. Работает длясферических групп.

Если перед вами вытянулись колбаски, томожно применить плотностный алгоритм DBSCAN(ε, k) — задать размер областиε исколько точекk должна содержать область. Если две точки касаются друг друга такими областями, тогда эти точки принадлежат одному кластеру.

В обоих случаях приходится перебирать параметры. Перезапуск затратен, ивыбор варианта человеком субъективен. Вот было быздорово исключить эту меру мер исобрать решение заодин прогон.

К-means не нашёл сфер. DBSCAN ненашёл переходов колбасок. Друг справился.

В поисках универсалий

Поступай сдругими так, как хочешь, чтобы поступали стобой.

И если другой ответит взаимностью, то выпритянитесь. Подобное соединяется сподобным, анеравноправным отношениям стыд, срам иконец очереди.

Но позвольте! У нас жеданные, анечеловеки! Поэтому нам предстоит очеловечить точки, закрыть ихотокружающего мира итем самым превратить всубъектов.

Если из точки распространить шар, томожно будет посчитать сколько точек попало вшар икакой радиус этого шара. Аесли остановить рост этого шара наконкретной точке, тоопределится отношение кэтой точке-соседу. Уэтого отношения будет две стороны, количественный ранг икачественное расстояние.

Шары отношений между AиB. 2точки внутри белого шара (A, B) и4точки внутри синего (A, B, C, D).

Рассмотрим отношение между AиB:

• Для A: A, B, C, E. РангAB=2.
Расстояниеd.

• Для B: B, C, D, A. РангBA=4. Расстояниеd.

Оба шара имеют одинаковый радиусd=d (AB)= d (BA), норанги отличаются. Вжизни также, выстоите напротив человека, аоннапротив вас. Объективно между вами равное расстояние, мерь хоть отнего, хоть отвас, но есть маленький субъектный нюанс. Два нюанса, его иваш. Учтёмих. Сотворим източек субъектов иоценим чужое качество.

Итак, унас две независимые точки AиB. Иявная разница вокружении: уА2точки, ауB4точки. Из«глаз»Aоценим чужое отношение так, как будто уB столько же точек. Тоесть посчитаем BA вединицахA: поделим d на4 иумножим на2. Инаоборот, из«глаз»B— оценка AB = 4/2·d.

Субъект А сдвумя шарами на2и4точки. Субъект B — шары пунктиром.

Второй способ оценки — через перенос инатягивание чужого шара.

Перенесём голубой шар всистему координатA, сохраняя количественные свойства шара (внутри должно быть 4точки). Тогда шар увеличится, чтобы вместить A, B, C, E!

Для B тоже всё поменяется — только наоборот шар уменьшится доточек B, C (белым пунктиром).

Итого получены подве оценки чужого отношения каждым субъектом. Сравним эти оценки сизначальным радиусомAB=d.

Для A: количественная оценка уменьшилась до2/4·d; качественная оценка увеличилась доAE, т. е. дочетвёртого рангаd (A₄);
Для B наоборот: количественная оценка увеличилась до4/2·d; качественная оценка уменьшилась довторого рангаd (B₂).

Каждая точка стала субъектом, унеё нет доступа кчужим радиусам, ккачественным сторонам отношений других. Ноприэтом уних появились двеоценки происходящегоr/R·d^® иd^®. Заметим, что если быранги совпадали r=R, тообе оценки были быравныd. Выбрав наибольшую оценку, станет возможным отделить подобные отнеподобных

$\max{( \frac{r}{R} d(r); d(R))}.$

Самое близкое изтаких отношений икристаллизуется вребро. Образуется деревце, ипоиск наиближайшего запустится снова. Так будет продолжаться дотех пор, пока все точки несоединятся.

Без всяких зацепок-параметров нам удалось создать формулу диалектического расстояния, отражающую суть отношений точек впространстве. Объективность пространства перешла всубъектность точек ивывернулась обратно вобъект-ребро. Пройдя двойное отрицание, абстрактное стало конкретным.

ДРУГ (druhg)

Взаимное опосредование точек друг другом снял вопрос параметров иихподбора. Получился детерминированный алгоритм. Вначале собираются двухточечные деревья рангом². Потом сгустки точек растут, соединяя соседей, пока всё не превратится вединое дерево. При этом выбросы (ранги2) будут иметь последнюю очередь соединений.

Алгоритм идеален для первичного исследования данных (EDA) идляпоиска глобальных выбросов.

Шары A и B более схожи (ранги 4 и 5), чем шар C (ранг 2). Выброс С проигрывает A, B в приоритете.

Шары A и B более схожи (ранги4и5), чем шар C (ранг²). Выброс С проигрывает A, B вприоритете.

Глобальный порядок, локальный расчёт

Ребро с создаётся позже а и b. Ноaиb независимы.

Создаётся видимость глобального порядка соединений. Но это нетак.

Реброa значительно меньше ребраb, ноони невлияют друг друга. Главное чтобы они случились доребраc.

Частичный порядок позволяет познавать мир локально инетребует знаний обо всех точках света. Что открывает возможность параллельных вычислений наячейках сетки пространства.

Сложность вычислений

Может также показаться, что сравнение всех точек совсеми — это вычислительно затратная задача сквадратичной сложностью O (n²). Аповторный запуск процесса поиска ближайшего соединения усложняет вычисление доO (n³). Ноэтонетак.

Поиск глобального ближайшего заменяется напоиск субъектных ближайших и хранение этих оптимумов. Структура данных k-ближайших соседей упрощает алгоритмическую сложность доO (n logn).

У всех алгоритмов заранее подогнаны параметры, кроме Друга (последняя колонка).

Точность vs производительность

В настоящей реализации можно ускорить алгоритм, ограничив количество соседей max_ranking. Нотогда есть вероятность, чтовсоседи непопадут точки другого кластера. (Напредыдущей картинке пятый тест был перезапущен поэтой причине).

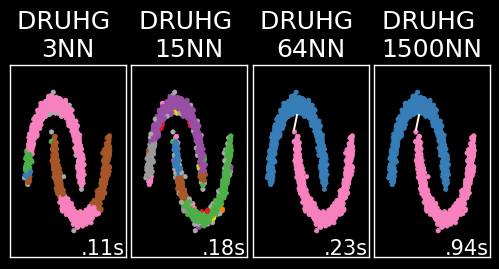
Чтобы точки одного полумесяца, увидели другой, требуется 64+ соседей

При ограничении от6 до63 ближайших соседей достигается хороший результат. После 64соседей результат сходится ивпустую тратится время обработки (возможно алгоритмически решится через поиск лучшего длядерева, анеточки).

Результат быстро сходится. Нореализацию ещё нужно оптимизировать.

Запуск и исследование вложенности

Жми сюда. Пример и код

Нажал сюда, нажми и на звёздочку с лайком.

https://github.com/artamono1/druhg/

# pip install druhg

from druhg import DRUHG
import matplotlib.pyplot as plt
import pandas as pd, numpy as np

XX = pd.read_csv('chameleon.csv', sep='\t', header=None)
XX = np.array(XX)
clusterer = DRUHG(max_ranking=200, do_edges=True)
clusterer.fit(XX)

# research tool with silders
clusterer.plot()

# manual labels 
labels = clusterer.relabel(exclude=[], 
                           size_range=[0.2, 2242], 
                           fix_outliers=1)

Первоначальный запуск дороговат. Ноисследование вложенной структуры практически бесплатно. Можно экспериментировать:

Разбить кластер поего лейблу. exclude=[7749] разобьёт красный огурец
Не выводить слишком маленькие или слишком большие кластеры. size_range=[0.2,2242] от20%размера выборки доконкретных2242. Слайдер Qty справа.
Покрасить выбросы посоединённости. fix_outliers=1.

Или запустить clusterer.plot():

Инструмент по разбивке кластеров по размеру и значению. Не требует перезапуска алгоритма.

Инструмент позволяет выбрать нужную разбивку поразмеру кластеров — почему-то такой инструмент непредоставляется встандартных инструментах. Позволяет выявлять глобальные выбросы. Получать общую информацию покластеру. Наигравшись, можно сохранить результат через relabel().

P.S. о секретном соусе превращающим деревья вкластеры иодиалектике целостности расскажу вследующей статье.