Начинаем изучать STM32: битовые операции27.09.2017 09:21

Небольшое отступление…

В прошлом уроке мы рассмотрели с чего начать, если вы решили изучать микроконтроллеры STM32: как настроить IDE, как создать простой проект, как откомпилировать программу и как запустить программу на выполнение. После полюбовались на перемигивание светодиодов на Discovery-плате =)

Начиная новую статью, я задумывал сразу же перейти к подробному разбору листинга программы, который заставлял попеременно перемигиваться наши светодиоды, но уже перейдя к написанию, я вдруг осознал для себя, что есть большое количество вопросов без ответа на которые — перейти к рассмотрению программы было бы преждевременно. И для себя я определил целый перечень таких вопросов:

Что же такое битовые операции? Как ими пользоваться?
Что такое регистры и как они связаны с битовыми операциями?
Из чего состоят микроконтроллеры STM32F0xx-серии, как осуществляется тактирование и чем обеспечена жизнь внутри МК?
Как происходит стартовая инициализация МК, зачем нужен startup-файл, что делает функция SystemInit? Объяснение на пальцах.
Из чего состоит библиотека CMSIS? Как в ней ориентироваться? Что полезного можно из нее извлечь и как ей пользоваться?

Именно с рассмотрения этих вопросов я хотел бы продолжить повествование о программировании STM32.

Основные логические операции

Только начиная изучать микроконтроллеры, слова «регистр» и «битовые операции» для меня казались чем-то таинственно загадочным и я долго не хотел переходить к рассмотрению данной темы. Но когда я более-менее разобрался с тем, что это такое я понял что зря откладывал изучение такой важной темы в дальний ящик. Битовые операции наверное самые распространенные операции в микроконтроллере и знание того, как и зачем их можно применять в нашей работе — откроет перед нами огромный потенциал возможностей для управления всем и вся в нашем МК!

Все мы на уроках информатики в школе знакомились с тем, что такое цифровая техника, почему она так называется, какие существуют основные логические операции.Все современные цифровые технологии основаны на двоичной математике и логических схемах. Микроконтроллер всегда оперирует только двумя состояниями: «ноль» — нет напряжения, «единица» — есть напряжение. Давайте немного освежим в голове знания о основных логических операциях т.к. они составляют основу всей цифровой техники.

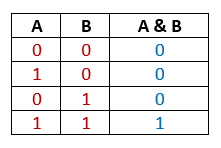
Конъюнкция — обозначается как «Логическое И» или «Логическое умножение». В сущности, результат от выполнения данной логической операции двух для выражений А и В подобен их умножению. То есть, выражение примет значение »1» в случае только если и А, и В имеют значение »1». Во всех других случаях будет значение »0». Может обозначаться как И, &&, AND, &
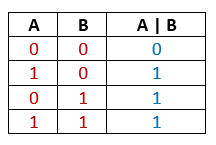
Дизъюнкция — обозначается как «Логическое ИЛИ» или «Логическое сложение». Результат от выполнения данной логической операции двух для выражений А и В подобен их сложению. То есть, выражение примет значение »1» в случае если хотя бы одно из выражений А и В имеют значение »1». Может обозначаться как ИЛИ, ||, OR, |.
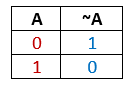
Инверсия — обозначается как «Логическое НЕ» или «Отрицание». Результат от выполнения данной логической операции двух для выражения А равен противоположному. То есть, выражение примет значение 1 в случае если выражение А равно 0 и наоборот. Может обозначаться как НЕ, !, NOT, ~.
Строгая дизъюнкция — обозначается как «Исключающее ИЛИ» или «Логическое сложение, исключающее ИЛИ». Результат от выполнения данной логической операции двух для выражений А и В примет значение 1 в случае если А и В имеют разные значения. Может обозначаться как Искл. ИЛИ, XOR, ^.

Битовые операции

Битовые операции — практически то же самое, что и логические операции только лишь с той разницей, что применяются они к битам и к числам двоичной системы.

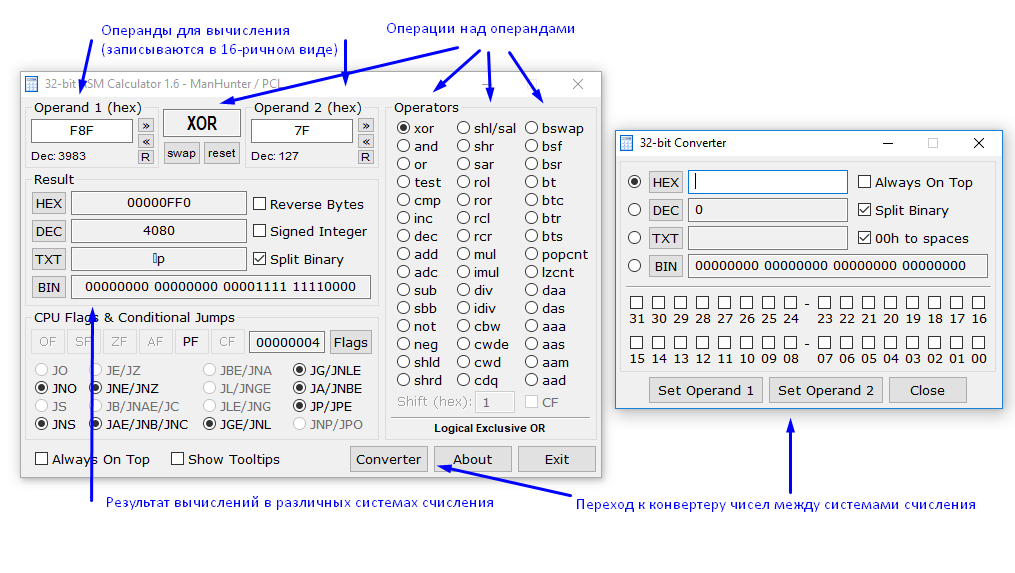
К слову говоря, для простоты изучения битовых операций я использовал программу 32-bit ASM Calculator от ManHunter. С помощью данной программы можно проверять результаты выполнения битовых операций, переводить числа из одной системы счисления в другую. Программа имеет интуитивно понятный интерфейс и после знакомства программа стала одним из основных инструментов в моей работе с микроконтроллерами. Небольшое пояснение к интерфейсу программы данно на изображении ниже:

Битовая операция «НЕ» — »~»
Если бит равен »1», то после выполнения операции «НЕ» он будет равен »0», и наоборот. Операция сразу же выполняется над всеми битами двоичного числа. Например, инвертируем число FF:

Битовая операция «И» — »&»
Если оба бита в разряде равны »1», то после выполнения операции «И» результат в разряде будет равен »1», но если хотя бы один из битов равен »0» тогда и результат будет равен »0». Операция так же выполняется поразрядно. Например, «умножим» два числа 0xFF0 и 0xF0F:

В результате мы увидим, что в тех разрядах где были единицы в обоих числах, в результате получились единицы, во всех остальных случаях — нули.

Рассмотрим варианты практического применения:

В ситуации, если нам необходимо сбросить конкретный бит или группу битов в ноль мы можем использовать маску. Думаю, будет нагляднее показать это на примере. Допустим, мы берем число и 0xF8F и нам надо чтобы 7-й бит стал вместо единицы нулем. Нет проблем, накидываем маску и снимаем галочку с нужного бита. Умножаем числа и получаем результат:
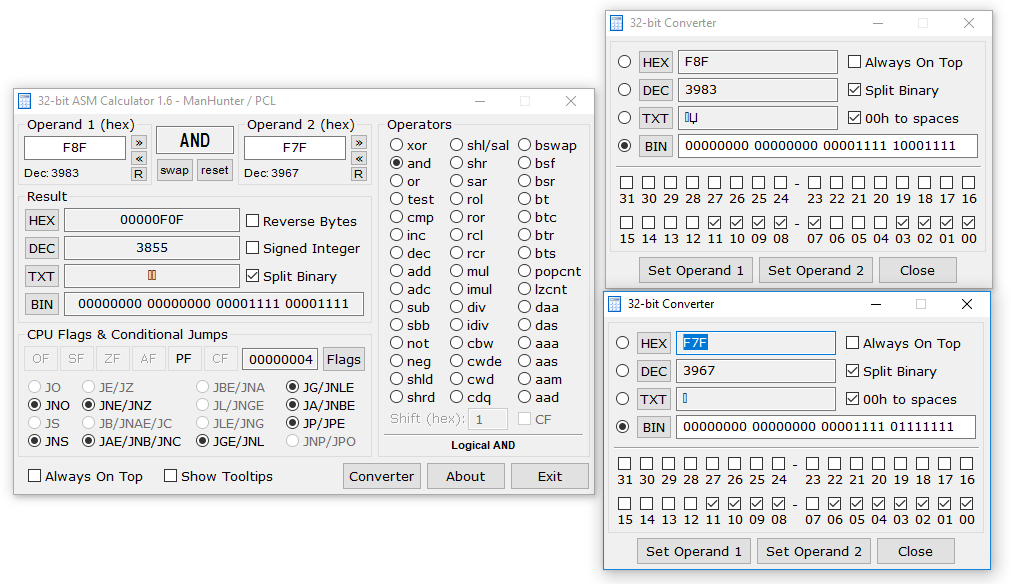
Если нам необходимо проверить конкретный бит в числе на 0 или 1 — мы так же используя маску проводим умножение. В маске мы устанавливаем бит, который хотели бы проверить. Если требуемый бит равен »0» — то результатом вычисления будет »0», если »1» то, соответственно,»1». Если мы хотим узнать, равен ли 7-й бит единицы — делаем соответствующую маску и умножаем наше число на маску. Все просто:

Если нам нужно проверить четность числа(имеется ввиду способность числа делиться на два) — то мы таким же образом проверяем 1-й бит, если он равен »1» — то число нечетное, если там »0» то число четное. Попробуйте сами, в целях обучения и формирования навыков, сделать данную проверку.

Битовая операция «ИЛИ» — »|»
Если один или оба из пары битов равен »1» то результат будет »1», иначе если оба бита равны »0» то результат будет равен »0». То есть, грубо говоря, производится сложение всех единиц в разрядах. Например если мы складываем два числа 0xF8F и 0×7F, то получим следующий результат:

Попробуйте самостоятельно поиграться с различными числами и понаблюдать за результатами.

Битовая операция «ИСКЛЮЧАЮЩЕЕ ИЛИ» — »^»
Если биты в разряде отличаются и не равны тогда результат будет »1», иначе »0». Например, если мы делаем XOR числа 0xF8F и 0×7F, то мы увидим что в разрядах в которых находятся отличные биты то там в результате получается »1» и в местах где биты одинаковые, будь то »0» или »1» — получился »0», в итоге мы получим следующий результат:

Рассмотрим варианты практического применения:

Если нам понадобилось инвертировать какие-либо биты в числе, можно используя маску с легкостью сделать это используя операцию XOR. Давайте сделаем инверсию 6 и 7 разряда в числе 0xF8 используя маску 0xC0. Результат вы можете посмотреть на изображении:
Бывают ситуации когда необходимо сравнить два регистра и определить равны они или нет. В этом случае нам необходимо значения регистров подвергнуть операции XOR. Если результат получился »0» — тогда регистры равны, иначе — не равны:

Битовые операции сдвига
Существует ряд интересных и порой чрезвычайно полезных битовых операций именуемых как операции сдвига. Двигать разряды можно как вправо, так и влево. В ходе данной операции происходит сдвиг всех разрядов двоичного числа на указанное количество позиций, при этом, в случае если сдвиг идёт влево — старший бит (самый левый) теряется, а в младший (самый правый) записывается »0». При логическом сдвиге вправо происходит обратная ситуация — младший бит (самый правый) теряется, а в старший записывается »0». Дополнительно хотелось бы отметить, что в случае 32-разрядных слов сдвигаются все 32 разряда целиком. Рассмотрим операции сдвига подробнее.

Cдвиг влево — »<<"
То, как происходит сдвиг вы можете увидеть на изображении ниже. Думаю, что всё достаточно очевидно:

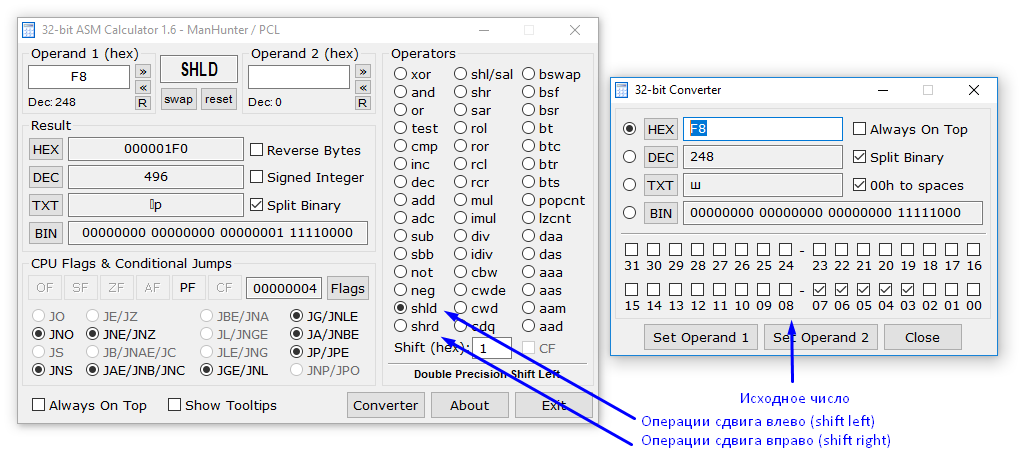
При двоичном сдвиге можно заметить одну интересную особенность. Сдвиг на один разряд умножает наше число на 2. Если сдвинуть на n разрядов наше число x то получится x * (2 * n). Попробуйте самостоятельно отследить эту закономерность через нашу утилку для подсчета. =)

Cдвиг вправо — »>>»
То, что получается в результате сдвига вправо достаточно наглядно отражено на изображении:

При двоичном сдвиге вправо можно заметить что происходит ситуация обратная сдвигу влево — число делится на 2 с при сдвиге в 1 разряд и после на 2 * n, где n — количество разрядов на которые произведен сдвиг. Так же попробуйте самостоятельно поиграться с числами и которые заведомо делятся на 2 нацело. И вопрос на засыпку — какой результат будет если вы поделите таким образом нечетное число?

Важное замечание. Если вы будете делать сдвиг для переменной с отрицательным знаком (signed) — освободившиеся позиции будут заполняться единичками.

В качестве заключения…

Многим начинающим данная тема может показаться дико скучной и может сложиться ощущение что ну вообще не понятно где и как можно применить эти знания. Спешу вас обнадежить, в ситуациях когда нужно поднять ту или иную ногу МК или записать параметр в какой-нить периферийный блок или модуль — там кругом и всюду будут требоваться знания битовых операций. Так как статья получилась достаточно объемной, рассмотрение регистров мы перенесем на следующий урок. Ну и в последующем можно использовать эту статью как шпаргалку.

В качестве домашнего задания попробуйте самостоятельно разобрать код нашей программы в блоке while (1) {… } и понять как же битовыми операциями мы включаем и выключаем наши светодиоды. Ну, а на следующем уроке я расскажу как оно происходит на самом деле!