Можно ли оставаться анонимным внутри государства, которое закрыло весь внешний Интернет?
Введение
Существующие популярные анонимные сети, подобия Tor или I2P, хороши своим прикладным использованием, а также относительно хорошей скоростью и лёгкостью настройки. Они также хороши и непосредственно в анонимизации трафика, когда нам необходимо скрыть истинную связь между отправителем и получателем, основываясь на принципе федеративности, то есть на свойстве, при котором узлы сети расположены в разных государствах, а сама цепочка маршрутизации проходит сквозь множество несвязанных между собой узлов. Но что делать, если государство единственно, как выстраивать маршруты в целях анонимизации, если нет никакого сетевого доступа в другие государства? Что делать, если все доступные государства находятся в своеобразном картеле, где сам принцип федеративности теряет свой основной замысел?
Принцип федеративности
Чтобы ответить на заданные вопросы, нам необходимо для начала разобрать сам принцип федеративности, а именно, то, на факте чего он держится и то, от чего он защищает. Для такой цели мы введём два новых термина — мощность федеративности и полиморфизм информации. Начнём с последнего.
Полиморфизм информации — это есть свойство изменчивости передаваемого объекта при множественной маршрутизации несколькими субъектами сети, разграничивающее связь субъектов посредством анализа объекта. Так например, если существует три субъекта сети {A, B, C} и объект P, который передаётся от A к B и от B к C соответственно, то внешний вид информации P1 и P2 должен определяться как [P1 = (A → B)] ≠ [P2 = (B → C)], где P ∉ {P1, P2} и P1 ≠ P2, (B не связывает {P1, P2} с P)и (A не связывает {P1, P} с P2) и/или (Cне связывает {P2, P} с P1). В большинстве случаев полиморфизм информации достигается множественным шифрованием объекта: [E2(E1(P)) = (A → B)] ≠ [E1(P) = (B → C)], (где E — функция шифрования), при котором интерстициальный, промежуточный субъект B становится неспособным связать {E2(E1(P)), E1(P)} с P, а субъект C неспособен связать {E1(P), P} с E2(E1(P)).
Мощность федеративности — количество государств, несвязанных между собой общими политическими интересами, через территорию которых проходит маршрутизация полиморфной информации. Из этого следует, что если сеть разворачивается лишь в пределах одного государства, то мощность федеративности по умолчанию будет равна единице. Также, из этого следует, что обычная, неполиморфная маршрутизация не будет повышать мощность федеративности, даже при учёте существования нескольких несвязанных государств.
И таким образом, сам принцип федеративности можно описать в виде двух необходимых критериев:
Необходимо использовать противоречия государств — вариативные и несогласованные законы, политические и империалистические интересы. Всё это есть моменты, при которых одно государство не будет выдавать информацию о своей сети другому государству. И чем более агрессивно настроены страны по отношению друг к другу, тем менее успешно они могут контролировать свои собственные ресурсы. В таком случае, необходимо строить сеть по федеративному принципу, чтобы узлы располагались на разных континентах мира, странах и государствах.
Необходимо использовать изменения информации в процессе её маршрутизации. При таком способе информация будет представлена в полиморфной и самоизменяющейся оболочке. Такой подход необходим в моменты, когда информация, приходящая из государства A в государство B, будет снова возвращаться на свою «родину» A. В качестве примера можно привести луковую маршрутизацию сети Tor, где само шифрование представлено в виде слоёв, которые каждый раз «сдирают», снимают при передаче от одного узла к другому.
На данном принципе базируется достаточное количество анонимных сетей, начиная с популярных — Tor, I2P, и заканчивая менее популярными — Mixminion, Crowds. В любом случае, нельзя не признать должного — принцип федеративности действительно рабочее средство, позволяющее достаточно эффективно скрывать истинную связь между двумя абонентами.
*Здесь также нужно взять во внимание конкретные уязвимости в реализации и проектировании тех или иных анонимных сетей, например Tor и Crowds уязвимы к timing-атакам, к которым, тем не менее, не уязвимы I2P и Mixminion. Это говорит о том, что уязвимости не лежат в плоскости принципа федеративности, а относятся исключительно к специфике архитектуры самой сети.
Проблема глобального наблюдателя
Принцип федеративности работает до тех пор, пока мощность федеративности больше единицы. И в этом кроется главная проблема, т.к. могут существовать сценарии, при которых становится невозможным применять принцип федеративности. Например, если государство X отгородится от всего остального мира, или если государство Y заблокирует большую часть VPN-сервисов и общеизвестных узлов анонимных сетей, или если абоненты (отправитель и получатель) находятся в одном и том же госудерстве Z, не ограничивающем связь, а следовательно и маршрутизацию со внешним миром, и при этом анонимная сеть A всё же уязвима к timing-атакам. В любом из этих сценариев, принцип федеративности оказывается в проигрышном положении.
В то время как последний случай можно относительно легко исправить просто сменив анонимную сеть A, уязвимую к timing-атакам, на анонимную сеть B, неуязвимую к timing-атакам, а со вторым случаем можно бороться посредством передачи/получения списков скрытых узлов (мостов) или арендой VPS/VDS сервера за границей в качестве дальнейшего VPN к анонимной сети, последний же, третий случай такими лёгкими манёврами не получится исправить. Само блокирование всей остальной сети приводит нас к проблеме глобального наблюдателя, в которой любые действия совершаются в заведомо замкнутой и прослушиваемой среде: наблюдателю становится известен весь маршрут передаваемого объекта, становится известен тот факт, кто его создал, когда он его создал, по какому маршруту он его перемещал, и в конечном итоге, становится известен тот факт, кому такой объект был передан.
Таким образом, все анонимные сети, базируемые на принципе федеративности, становятся уязвимы к проблеме глобального наблюдателя, потому как модель угроз на базе федеративности не предполагает решения проблемы при условии существования единого и монопольного наблюдателя. Реализация дополнительных «фич» со стороны анонимных сетей, например в лице примитивной генерации мусорного трафика, лишь затушёвывает основное противоречие, но не решает его окончательно. При достаточно длительном периоде рассмотрения действий в сети можно будет замечать и отделять мусорный трафик от истинного, потому как первый есть лишь наложение на второй. Таким образом, если не будет существовать истинного трафика, то суммарный объём всего трафика снизится до мусорного и тем самым, глобальный наблюдатель уже апостериори, по истечению времени анализа, будет знать действительную разницу между разнородным видом трафика. И как следствие, в следующих своих анализах, глобальный наблюдатель априори будет учитывать эту разницу.
Теоретически доказуемая анонимность
Несмотря на кажущуюся затруднительную ситуацию, существует ряд анонимных сетей способных противостоять глобальному наблюдателю, будучи расположенными в заведомо враждебной, прослушиваемой и замкнутой среде. Отличительной особенностью таковых сетей является тот факт, что глобальный наблюдатель становится неспособным выявляться закономерности маршрутов или отличий в типе трафика. Более формальное определение таковых сетей звучит следующим образом.
Анонимными сетями с теоретически доказуемой анонимностью принято считать замкнутые, полностью прослушиваемые системы, в которых становится невозможным осуществление любых пассивных атак (в том числе и при существовании глобального наблюдателя) направленных на деанонимизацию факта отправления и/или получения информации, или на деанонимизацию связи между отправителем и получателем с минимальными условностями по количеству узлов неподчинённых сговору. Говоря иначе, с точки зрения пассивного атакующего, апостериорные знания, полученные вследствие наблюдений, должны оставаться равными априорным, до наблюдений, тем самым сохраняя равновероятность деанонимизации по N-ому множеству субъектов сети.
На сегодняшний момент времени существует три вида задач анонимизации с теоретически доказуемыми моделями. На основе таковых задач могут быть созданы непосредственно сами анонимные сети.
Проблема обедающих криптографов (анонимные сети: Herbivore, Dissent)
Задача на базе очередей (анонимные сети: Hidden Lake, M-A)
Задача на базе увеличения энтропии (анонимные сети: отсутствуют)
Отличием анонимных сетей от их задач является сам фактор использования и механизм функционирования, где одно является теорическим рассуждением (задача), другое является практичкой реализацией (сеть). Так например, Tor — это уже готовая сеть, в то время как луковая маршрутизация — её механизм функционирования. Ровно также и здесь, Herbivore — это уже готовая сеть, в то время как проблема обедающих криптографов — её механизм функционирования.
Проблема обедающих криптографов является достаточно старой и устоявшейся задачей в научных кругах, что в действительности является очень хорошим качеством. Но стоит учитывать, что две оставшиеся задачи являются относительно новыми, им буквально всего один-два года, что может вызвать вполне оправданный скептицизм. В таком случае, о последних задачах вы можете почитать в ссылках указанных выше или более подробно, и во всех нюансах, вы можете почитать в работе — Абстрактные анонимные сети.
Вкратце о проблеме обедающих криптографов
Первой теоретически доказуемой анонимной сетью (как ядро) становится задача обедающих криптографов. Выглядит она так (не буду пересказывать о том, как криптографы обедают и о том, что существует некий АНБ, раскажу вкратце): существует три участника сети {A, B, C}. Один участник хочет послать 1 бит информации по сети (либо 1, либо 0 соответственно), но таким образом, чтобы другие субъекты не узнали кто отправил данную информацию. Предполагается, что таковые участники соединены между собой, тем самым имеют безопасный канал связи, а также имеют расписание по которому в каждый момент времени T генерируется новый бит.
Предположим, что участник A хочет отправить информацию по сети так, чтобы {B, C} эту информацию получили, но не смогли узнать, кто действительно является отправителем. Иными словами, для B это может быть {A, C}, а для C это {A, B} с вероятностью 50/50. Все участники начинают согласовывать общий бит со своими соседями (в момент времени T, конечно же). Предположим, что участники {A, B} согласовали бит = 1, {B, C} = 0, {C, A} = 1.
Далее каждый участник сети XOR’ит (операция исключающее ИЛИ) биты со всех своих соединений: A = 1 xor 1 = 0; B = 1 xor 0 = 1; C = 0 xor 1 = 1. Данные результаты обмениваются по всей сети и XOR’ятся каждым её участником: 0 xor 1 xor 1 = 0. Это говорит о том, что участник A передал бит информации = 0. Чтобы субъект A мог передать бит = 1, ему необходимо добавить операцию НЕ в своём вычислении, то есть A = НЕ (1 xor 1) = 1. В итоге, все вычисления прийдут к такому результату: 1 xor 1 xor 1 = 1.Таким образом, можно передать 1 бит информации полностью анонимно (конечно же со стороны определения теоретически доказуемой анонимности).

Сеть на базе задачи обедающих криптографов при трёх участниках {A, B, C}
Предположим, что один из участников, либо B, либо C захочет деанонимизировать либо {A, C}, либо {B, C} соответственно (то есть узнать, кто является отправителем информации). Тогда ему потребуется узнать согласованный секрет со стороны другой линии связи, что является сложной задачей (если конечно не был произведён сговор нескольких участников). Таким образом, атака со стороны внутреннего пассивного наблюдателя становится безрезультатной. Со стороны внешнего глобального наблюдателя такая же ситуация, потому как он видит лишь переадресации зашифрованных битов (потому как используется безопасный канал связи) в один момент времени T всеми участниками сети.
Вкратце о задаче на базе очередей
Предположим, что существует три участника {A, B, C}. Каждый из них соединён друг c другом (не является обязательным критерием, но данный случай я привёл исключительно для упрощения). Каждый субъект устанавливает период генерации информации = T. В отличие от DC-сетей, где требуется синхронизация установки периода по времени, в задаче на базе очередей такое условие не является обязательным. Иными словами, каждый участник сети может начать генерировать информацию с периодом = T в любое время, без предварительной кооперации/синхронизации с другими участниками. У каждого участника имеется своё внутренее хранилище по типу FIFO (первый пришёл — первый ушёл), можно сказать имеется структура «очередь».
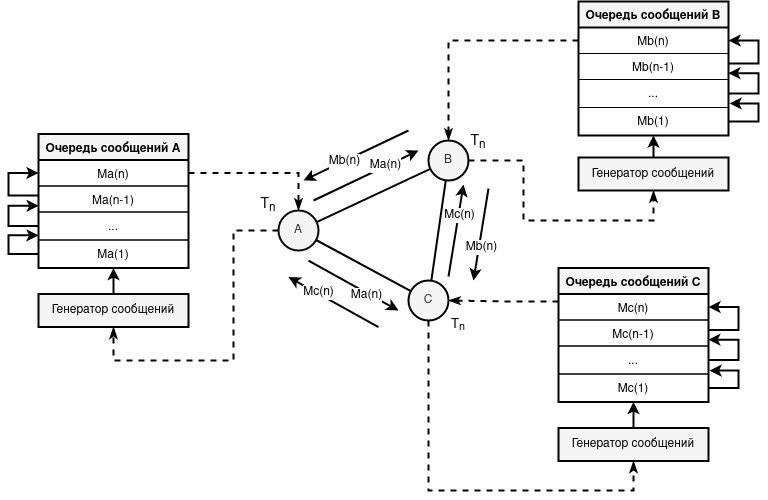
Сеть на базе очередей при трёх участниках {A, B, C}
Предположим, что участник A хочет отправить некую информацию одному из участников {B, C}, так, чтобы другой участник (или внешний наблюдатель) не знал, что существует какой-либо факт отправления. Каждый участник в определённый период T генерирует сообщение. Такое сообщение может быть либо ложным (не имеющее никакого фактического содержания и никому по факту не отправляется, заполняясь случайными битами), либо истинным (запрос или ответ). Отправить раньше или позже положенного времени T никакой участник не может. Если скопилось несколько запросов одному и тому же участнику, тогда он их ложит в свою очередь сообщений и после периода T достаёт из очереди и отсылает в сеть.
Таким образом, внешний глобальный наблюдатель будет видеть лишь картину, при которой каждый участник в определённо заданный период времени T отправляет некое сообщение всем остальным узлам сети, что не даёт никакой информации о факте отправления, либо получения. Внутренние пассивные участники также неспособны узнать коммуниицирует ли один из участников в данный период времени с каким-либо другим, т.к. предполагается, что шифрованная информация не выдаёт никаких данных об отправителе и получателе непосредственно.
Вкратце о задаче на базе увеличения энтропии
Предположим, что существует три субъекта {A, B, C} и существует глобальный наблюдатель, целью которого является определение отправителя и получателя в сети. Предположим также, что все субъекты данной системы не заинтересованы в деанонимизации друг друга (эта условность будет служить лишь упрощением, на практике она в полной мере не обязательна). Анонимизация здесь строится на итеративной схеме, иными словами, чем больше вы будете отправлять сообщений, тем лучше качество анонимности будет становиться.
Предположим, что сеть базируется на схеме запрос-ответ, иными словами, когда один пользователь отправит запрос, то другой пользователь должен будет на него ответить.
Предположим, что мы являемся субъектом A, а получателем для нас будет являться субъект C. Мы знаем публичные ключи всех пользователей {B, C}. Шифрование происходит публичным ключом получателя. Предполагается, что никто не сможет расшифровать сообщение кроме узла обладающего приватным ключом. Чтобы отправить сообщение M, нам необходимо проделать одно из следующих действий с вероятностью ½:
Зашифровать M открытым ключом пользователя C и отправить шифрованное сообщение EC (M) всем пользователям сети, то есть пользователям B и C.
ИЛИ
Зашифровать M дважды, сначала открытым ключом пользователя C, а затем открытым ключом пользователя B и отправить шифрованное сообщение EB (EC (M)) всем пользователям сети, то есть пользователям B и C.
На первый взгляд кажется, что получилась какая-то ересь. Во-первых, глобальный наблюдатель априори знает, что пользователь A является отправителем информации M, потому как таковой является инициатором связи. Во-вторых, предполагается, что глобальный наблюдатель также знает внутренний механизм анонимизации трафика, а потому знает саму условность ½. Как следствие, если после отправленного сообщения последует сразу следующее и на этом моменте вся связь прервётся, то тот, кто переправит сообщение — является истинным получателем, сгенерировавшим ответ. Таким образом, на первый взгляд кажется, что эта схема обречена на провал.
Но мы держим в голове тот факт, что схема анонимизации итеративна и с каждым проходом лишь увеличивает анонимность. Пока что мы проигнорируем первый пункт с инициатором связи и попытаемся рассмотреть второй пункт. Действительно, если связь прервётся, то глобальный наблюдатель сможет узнать кто являлся получателем сообщения. Но теперь, что если связь будет продолжаться, хотя бы ещё одну итерацию, то насколько увеличится анонимность?
Для лёгкости восприятия, мы теперь будем исходить из лица внешнего глобального наблюдателя. Я буду указывать (A → B) как факт отправления, что A отправил B информацию. (ИЛИ) будет говорить о неопределённости со стороны наблюдателя.
Если мы далее продлим связь на плюс одну итерацию, то итоговая схема будет выглядить следующим образом:
(A → B ИЛИ A → C) = запрос (1)
[Внешний наблюдатель знает лишь факт отправления и то, кто отправил сообщение — A, но пока не знает кто является получателем](B → A ИЛИ C → A) = ответ (1)
[Внешний наблюдатель знает, что с вероятностью ½ пакет мог быть зашифрован лишь единожды и тогда B или C сразу отправит пользователю A ответ]ИЛИ
(B → C ИЛИ C → B) = маршрутизация (1)
[Внешний наблюдатель знает, что с вероятностью ½ пакет мог быть зашифрован дважды и тогда B или C будет являться маршрутизатором к C или B соответственно](B → A ИЛИ C → A) = ответ (1)
[Внешний наблюдатель знает, что с вероятностью ½ пакет мог быть зашифрован дважды и тогда B или C после этапа маршрутизации отправит пользователю A ответ]ИЛИ
(B → A ИЛИ B → C ИЛИ C → A ИЛИ C → B) = запрос (2)
[Внешний наблюдатель предполагает, что ответ мог быть уже выдан на этапе 2., а на этапе 3. мог быть сгенерирован совершенно новый запрос]
Всё, как только вступает в действие новая итерация, а конкретно новый запрос — увеличивается энтропия, как мера неопределённости, ровно на 1 бит. В то время как раньше, до второго запроса внешний наблюдатель мог со 100% вероятностью определить отправителя, то теперь вероятность определения отправителя составляет 50% (из B и C), как только начинается вторая итерация запросов.
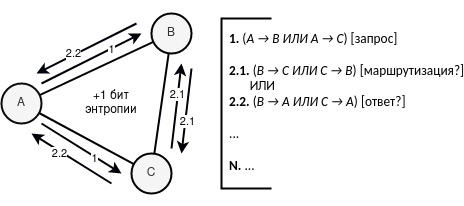
Сеть на базе увеличения энтропии при трёх участниках {A, B, C} (увеличение энтропии на единицу)
При этом, новая итерация запроса рушит уверенность в получателе первой итерации, потому как происходит пересечение первой незавершённой итерации запрос-маршрутизация-ответ со второй итерацией запрос. Таким образом, энтропия, по-факту увеличивается «авансом» к отправителю, потому как сначала она увеличивается для получателя, а только потом переходит на отправителя. Иными словами, если мы уверены, что цепь событий продолжится, то на втором этапе для получателя будет повышена энтропия на 1 бит, и только потом, на следующем — третьем этапе, энтропия будет повышена для отправителя.
Таким образом, хоть при первой итерации мера неопределённости равнялась 0 бит, но как только достигается вторая итерация, неопределённость увеличивается на бит и как следствие, делит ранее 100%-ую вероятность вдвое. Вышеописанную схему можно представить ещё более лёгким образом, в виде перекрытия запросов и ответов:
запрос (1)-ответ (1)-запрос (2)-ответ (2)
запрос (1)-маршрутизация (1)-ответ (1)-запрос (2)
В таком случае, мы видим, что запрос (1)=запрос (1) в любом случае равны друг другу и как следствие вероятность определения истинности равна 100%. Далее, как только начинается противоречие между первым и вторым определением — зарождается неопределённость, но только «авансом», не окончательно. Таким образом, на этапе ответ (1)=маршрутизация (1) мы уже не знаем какая конкретно происходит операция со стороны получения ответа. Если идти далее, как только появляется запрос (2)=ответ (1), то мы уже не сможем со 100% вероятностью утверждать, что не происходит совершенно нового запроса.
Если таким же образом продолжать цепь событий, то энтропия будет каждый раз увеличиваться на единицу. Визуально это можно изобразить на вышеприведённом рисунке. В результате, глобальному наблюдателю остаётся лишь догадываться кто является отправителем и получателем, и с каждым разом вероятность определения старых запросов будет постепенно «растворяться» во множестве новых.
Все анонимные сети с теоретически доказуемой анонимностью обладают в определённой степени схожими характеристиками. Возможно таковые являются основополагающими для всех сетей с теоретически доказуемой моделью, т.к. пока неизвестны другие задачи, которые бы могли игнорировать нижеуказанные пункты.
Мусорный (ложный) трафик является неотъемлемой частью теоретически доказуемых анонимных сетей. В то время как в других анонимных сетях ложный трафик лишь накладывается на истинный, в теоретически доказуемых сетях ложный трафик порождается самим ядром, механизмом, задачей анонимизации.
Передаваемый объект транспортируется всем узлам сети, не имея точного и чёткого маршрута своего движения. Иными словами, нагрузка всей сети определяется линейно от количества её участников, то есть за O (N).
За счёт первого и второго пункта, анонимные сети с теоретически доказуемой анонимностью могут работать лишь в пределах малых групп участников, например 30–100 узлов, в отличие от тех же анонимных сетей Tor и I2P, у которых нет таких специфичных пунктов, а следовательно и ограничений.
При этом есть также ещё интересные моменты:
Ранее могло показаться, что полиморфизм информации необходим всегда в анонимных сетях, и являлся в некой степени характерной особенностью самих анонимных сетей. Но как оказалось, анонимные сети могут вовсе не обладать полиморфизмом информации и оставаться при этом анонимными сетями, что и показывает своим существованием задача на базе очередей.
Основываясь лишь и только на проблеме обедающих криптографов, а также на задаче очередей можно было бы выдвинуть ложное предположение, что все теоретически доказуемые сети должны быть последовательны в своих запросах (исключать параллельность), основываясь лишь и только на очередях (локальных или глобальных). Но задача на базе увеличения энтропии рушит эту теорию. Хоть и действительно, если узел будет генерировать куда больше запросов в один момент времени, чем большая часть сети, то это станет подозрительным, тем не менее, сама случайность может сыграть противоположное действие. Поэтому перед выполнением параллельных запросов остаётся лишь высчитать вероятность появления N-ой параллельности. Если вероятность достаточно большая, то и сама параллельность становится вполне допустимой в сети.
При поверхностном рассмотрении теоретической доказуемости может показаться, что выдвигаемые задачи порождают лишь одноранговые сетевые архитектуры, исключая при этом какую бы то ни было гибридность. На самом же деле, задачи вполне могут существовать и быть реализованы внутри гибридных систем. Так например, задача на базе очередей может быть адаптирована под предоставление анонимности исключительно отправителя, но не получателя. В такой системе гибридность становится необходимой, чтобы собирать анонимные сообщения в кучу и далее их постепенно раскрывать, проводя через несколько узлов.
Сетевые архитектуры и модели

Многоранговые сети делятся на две модели: централизованные и распределённые. Централизованная или классическая клиент-серверная архитектура является наиболее распространённой моделью из-за своей простоты, где под множество клиентов выделяется один сервер, выход из строя которого приводит к ликвидации всей сети. Распределённая многоранговая система предполагает множество серверов, принадлежащих одному лицу или группе лиц с общими интересами, на множество клиентов, тем самым решая проблему уничтожения сети при выходе из строя одного или нескольких серверов. Из вышеописанного также следует, что классическая централизованная структура является лишь частным случаем более общей распределённой модели, или иными словами, сам факт распределённости становится следствием централизации. Сети на основе многоранговой архитектуры расширяются изнутри, относительно своего ядра, и не допускают расширения извне.
В одноранговых (peer-to-peer) системах все пользователи однородны, имеют одинаковые возможности, могут представлять одни и те же услуги маршрутизации. Сами одноранговые сети могут быть разделены на три модели: централизованные, децентрализованные и распределённые (последняя — условно). Централизованные одноранговые сети представляют собой соединения на базе одного или нескольких, заранее выделенных или динамически выделяемых серверов-ретрансляторов, исключение которых приводит к блокированию всей сети. Отсутствие прав серверов в такой модели начинает порождать равноправность их клиентов. Распределённые сети не выделяют какой-либо центр или узел связи, сохраняя факт одновременной и полной коммуникации узла со всеми другими узлами, иными словами, со всей сетью. Иногда под распределённой связью подразумевают также необходимое N-ое количество соединений, необязательно со всей сетью. В децентрализованных сетях становится возможным образование неравномерного распределения соединений и появление «неофициальных» узлов-серверов, часто используемых другими узлами в качестве последующей маршрутизации. Таким образом, децентрализованная модель, в своём определении, начинает быть более подверженной концентрированию линий связи, чем распределённая модель. Тем не менее, распределённая модель является лишь конфигурацией децентрализованной и полноценно, в отрыве от последней, рассматриваться не может. Сети на основе одноранговой архитектуры расширяются извне, за исключением начальной фазы одноранговой централизации.
Гибридная система объединяет свойства многоранговых и одноранговых архитектур, пытаясь взять и удержать как можно больше положительных и меньше отрицательных качеств. Сама гибридность системы может рассматриваться в разных значениях и проявлениях, как пример на уровне топологий: «шина + кольцо», «кольцо + полносвязная», «звезда + ячеистая» и т.д., или на уровне прикладного рассмотрения: «одноранговая + многоранговая». Плюсом многоранговых архитектур становится возможность разделения логики на серверную и клиентскую, а также более быстрая и/или статичная скорость маршрутизации. Плюсом одноранговых архитектур становится высокая отказоустойчивость за счёт внешнего расширения сети и возможность построения безопасной, а также масштабируемой «клиент-клиент» связи. Минусом гибридных архитектур на ранних стадиях развития является их возможный, осуществимый и более вероятностный переход в многоранговые системы (по сравнению с одноранговыми) за счёт большого уплотнения серверов принадлежащих одному лицу, либо группе лиц с общими интересами.
Стоит также сказать, что теоретически доказуемая анонимность не является абсолютной анонимностью, в том простом плане, что первая ограничена лишь и только пассивными атаками, в то время как вторая защищена в общем от всех возможных атак. Первую возможно доказать лишь за счёт собственной ограниченности пассивных наблюдений, которые более не могут предоставить новые векторы нападений, что нельзя сказать об активных наблюдателях, атаки которых могут успешно синтезироваться, улучшаться, обновляться. Поэтому существование абсолютной анонимности, в тех или иных условиях, остаётся всегда под вопросов, что, тем не менее, не распространяется на теоретическую анонимность.
Пример активной атаки (запрос-ответ)
Предположим, что существует всего три узла в сети {A, B, C}. Мы являемся атакующим под точкой A. В нашем распоряжении есть идентификатор ID (допустим публичный ключ) одного из субъекта: либо B, либо C. Нашей целью становится связывание данного идентификатора с реальным сетевым адресом, тобишь целью становится узнать и связать реальный IP-шник узла с ID.
Если мы можем исполнять роль как глобального наблюдателя, так и внутреннего узла, в роли узла — A, то сама атака становится примитивной. Мы начинаем генерировать запрос к одному из узлов {B, C} по идентификатору ID. Т.к. архитектура сети построена по принципу «запрос-ответ», то на любой запрос будет сгенерирован свой ответ. Т.к. анонимная сеть является теоретически доказуемой, то просто проанализировав трафик сети мы ничего не получим, поэтому нам необходимо проделать некую активную манипуляцию, а именно — заблокировать на время одного участника: либо B, либо C от всей другой сети.
И так, мы блокируем участника B, отправляем сгенерированный запрос по идентификатору ID. Если спустя время мы получаем ответ, то получателем является узел C, и как следствие, мы связываем ID с IP адресом. Иначе, если мы не получаем ответ, то получателем является узел B (так как он был заблокирован), и также связываем его IP адрес с ранее известным ID. В итоге, мы деанонимизировали участника сети и если кто-то будет отправлять сообщения с данным ID, то мы уже будем знать кто конкретно сидит под данным идентификатором.
Скрытие факта анонимизации
При теоретически доказуемой анонимности глобальному наблюдателю становится проблематичным выявить само состояние субъекта в сети, а именно совершает ли он сейчас или когда-либо совершал определённое действие (отправление / получение информации) или всё время бездействовал. Тем не менее, это не мешает глобальному наблюдателю выявить принадлежность субъекта к этой сети по характерным и специфичным особенностям самой системы.
Так например, при задаче на базе очередей достаточно лишь выявить, что субъект каждый заданный интервал времени = T отправляет шифрованные сообщения в сеть. В проблеме обедающих криптографов достаточно сравнивать лишь массовость XOR операций. Из приведённого списка теоретически доказуемых моделей наверное наименее подверженная к чёткому определению привязанности субъекта к анонимизации трафика является модель на базе увеличения энтропии за счёт отсутствия конкретных паттернов поведения.
Тем не менее, что делать с оставшимися двумя задачами? Ответ на этот вопрос может лежать в нескольких плоскостях.
Первый и самый очевидный — это генерировать в случайный промежуток времени ложный трафик. К сожалению, это будет лишь затушёвывать анонимизирующий трафик.
Второй способ — это растягивать период генерации, в таком случае наблюдателю потребуется больше времени для сопоставления закономерностей. Но, применив единожды данную закономерность, наблюдатель сможет впоследствии более эффективно выявлять анонимизацию трафика.
Третий способ — сделать сами периоды случайными. Такой способ не сработает для DC-сетей (проблема обедающих криптографов), потому как в данном типе задачи необходима сильная синхронизация участников сети по периоду генерации трафика, что нельзя сказать о задаче на базе очередей. В задаче на базе очередей каждый участник устанавливает свой период генерации информации, а потому и сам может в определённые промежутки времени его менять.
Помимо механизма анонимизации глобальный наблюдатель может выявлять размер передаваемой информации. Большинство анонимных сетей передают информацию в статичном объёме, что вполне оправдано, т.к. предотвращает уязвимости по типу передаваемых данных. Тем не менее, это же явление может быть решающим в блокировании всей сети. Чтобы этого избежать, размер данных должен быть одновременно и статичным, и динамичным. Может показаться, что это прямое противоречие, но это не совсем т
