Моя численная проверка гипотезы «Абсолютных курсов»
Привет, Хабр!
Мне показалась интересной данная публикация: Получаем абсолютные курсы из парных кросс-курсов валют и я захотел проверить возможность найти этот аааабсолютный курс валюты через численное моделирование, вообще отказавшись от линейной алгебры.
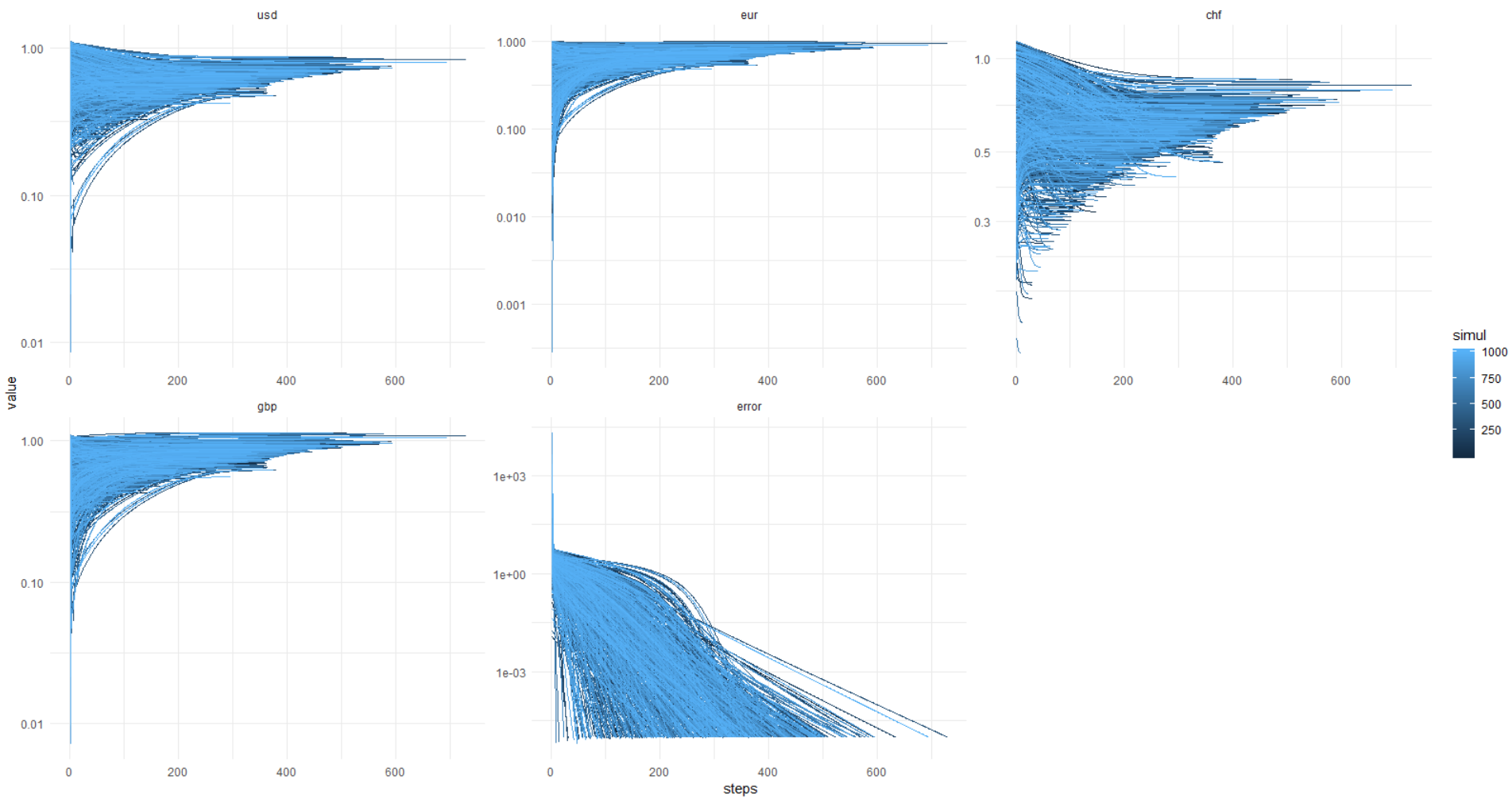
Результаты получились интересными.
Эксперимент будет небольшим: 4 валюты, 6 валютных пар. Для каждой пары одно измерение курса.
Итак, начнем
Гипотеза в том, что стоимость любой валюты можно выразить неким значением, которое будет учитывать стоимости других валют, в которых она котируется, при том, что другие валюты сами будут выражены в стоимости всех других валют. Это интересная рекурсивная задача.
Имеется 4 валюты:
- usd
- eur
- chf
- gbp
Для них был набраны валютные пары:
- eurusd
- gbpusd
- eurchf
- eurgbp
- gbpchf
- usdchf
Обратите внимание, что если число валют n = 4, то число пар k = (n ^2 — n) / 2 = 6. Нет смысла искать usdeur, если котируется eurusd…
В момент времени t был замерен курс валютных пар у одного из провайдеров:
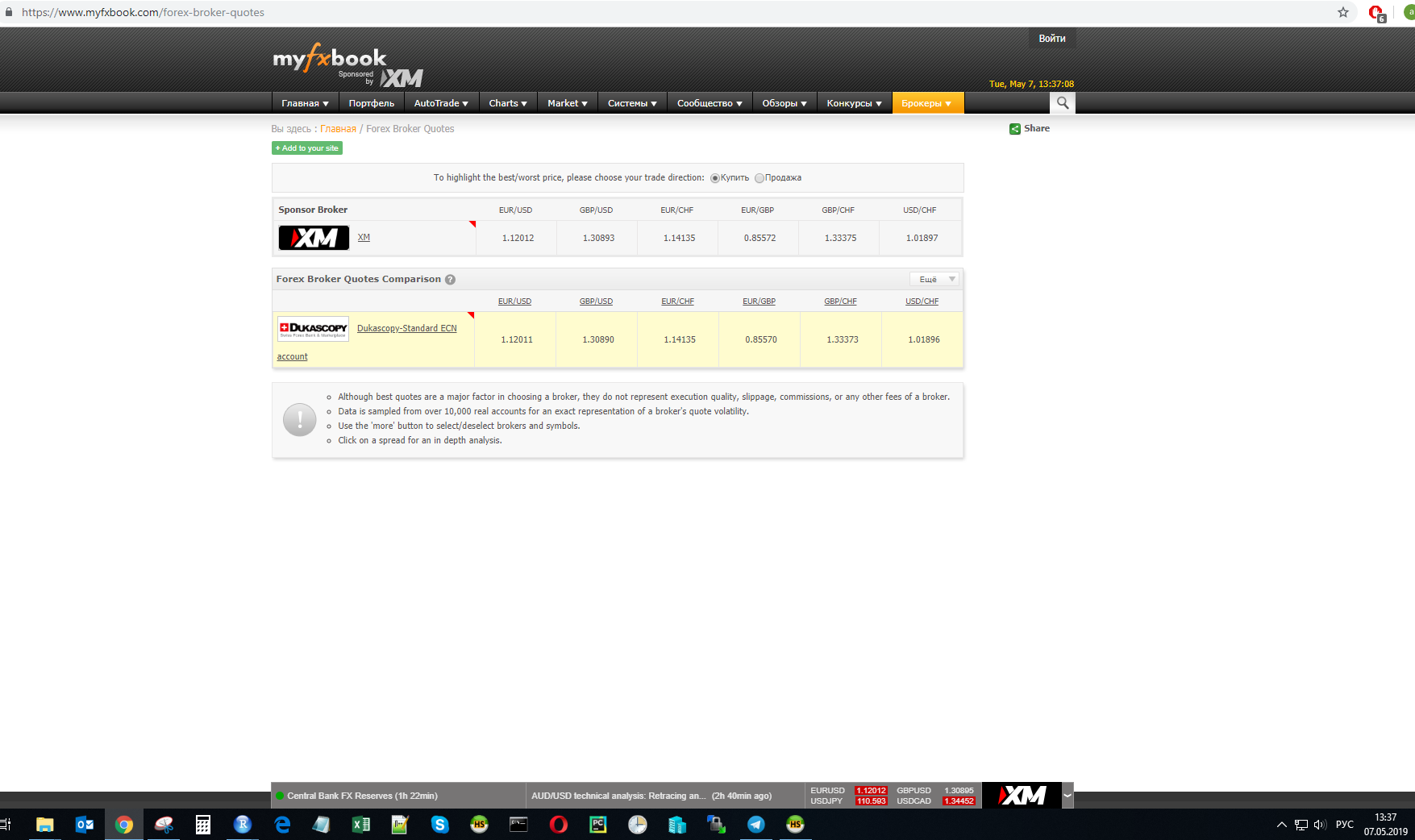
Расчеты будут проводиться для этих значений.
Математика
Я решаю задачку, аналитически беря градиент функции потерь, которая по сути есть система уравнений.
Код эксперимента будет на языке R:
#set.seed(111)
usd <- runif(1)
eur <- runif(1)
chf <- runif(1)
gbp <- runif(1)
# snapshot of values at time t
eurusd <- 1.12012
gbpusd <- 1.30890
eurchf <- 1.14135
eurgbp <- 0.85570
gbpchf <- 1.33373
usdchf <- 1.01896
## symbolic task ------------
express <- expression(
(eurusd - eur / usd) ^ 2 +
(gbpusd - gbp / usd) ^ 2 +
(eurchf - eur / chf) ^ 2 +
(eurgbp - eur / gbp) ^ 2 +
(gbpchf - gbp / chf) ^ 2 +
(usdchf - usd / chf) ^ 2
)
eval(express)
x = 'usd'
D(express, x)
eval(D(express, x))
R позволяет с помощью ф-ии stats: D брать производную функции. Например, если мы хотим продифференцировать по валюте USD, получаем такое выражение:
2 * (eur/usd^2 * (eurusd — eur/usd)) + 2 * (gbp/usd^2 * (gbpusd —
gbp/usd)) — 2 * (1/chf * (usdchf — usd/chf))
Чтобы уменьшить значение функции express, мы будем выполнять градиентный спуск и сразу понятно (видим квадратные разницы), что минимальное значение будет равно нулю, что нам и нужно.
-deriv_vals * lr
Шаг градиентного спуска будет регулироваться параметром lr и все это взято с отрицательным знаком.
То есть, человеческими словами, подберем курсы 4-х валют так, чтобы все валютные пары в эксперименте получили значения равные исходным значениям этих пар. Ммм, решим задачку — в лоб!
Результаты
Чтобы не растягивать, сразу сообщу вам следующее: эксперимент в целом удался, код заработал, ошибка ушла близко-близко к нулю. Но тут я заметил, что результаты всегда получаются разными.
Вопрос знатокам: похоже, эта задача имеет неограниченное количество решений, но в этом я полный ноль, думаю, мне подскажут в комментариях.
Чтобы убедиться в (не)стабильности решения, я провел симуляцию 1000 раз, не зафиксировав сид ГПСЧ для стартовых значений ценности валют.
А здесь идет картинка из ката: error достигает 0,00001 и меньше (так задана оптимизация) всегда, при этом значения валют уплывают черти-знает куда. Получается, всегда разное решение, господа!
Еще раз эта картинка, y-axis в оригинальных единицах (не лог.):
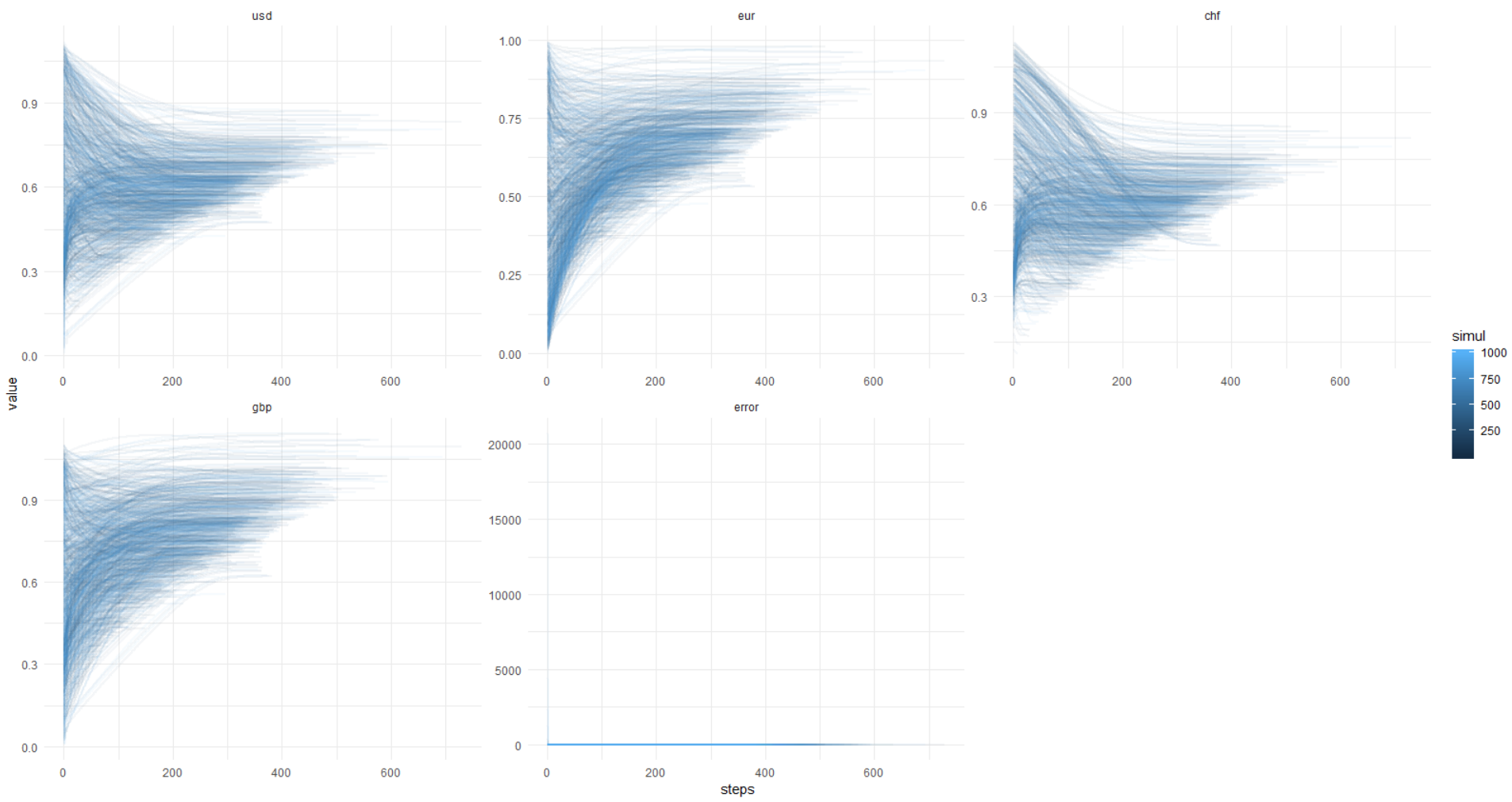
Чтобы вы могли повторить это, ниже я прикладываю полный код.
# clear environment
rm(list = ls()); gc()
## load libs
library(data.table)
library(ggplot2)
library(magrittr)
## set WD --------------------------------
# your dir here ...
## set vars -------------
currs <- c(
'usd',
'eur',
'chf',
'gbp'
)
############
## RUN SIMULATION LOOP -------------------------------
simuls <- 1000L
simul_dt <- data.table()
for(
s in seq_len(simuls)
)
{
#set.seed(111)
usd <- runif(1)
eur <- runif(1)
chf <- runif(1)
gbp <- runif(1)
# snapshot of values at time t
eurusd <- 1.12012
gbpusd <- 1.30890
eurchf <- 1.14135
eurgbp <- 0.85570
gbpchf <- 1.33373
usdchf <- 1.01896
## symbolic task ------------
express <- expression(
(eurusd - eur / usd) ^ 2 +
(gbpusd - gbp / usd) ^ 2 +
(eurchf - eur / chf) ^ 2 +
(eurgbp - eur / gbp) ^ 2 +
(gbpchf - gbp / chf) ^ 2 +
(usdchf - usd / chf) ^ 2
)
## define gradient and iterate to make descent to zero --------------
iter_max <- 1e+3
lr <- 1e-3
min_tolerance <- 0.00001
rm(grad_desc_func)
grad_desc_func <- function(
lr,
curr_list
)
{
derivs <- character(length(curr_list))
deriv_vals <- numeric(length(curr_list))
grads <- numeric(length(curr_list))
# symbolic derivatives
derivs <- sapply(
curr_list,
function(x){
D(express, x)
}
)
# derivative values
deriv_vals <- sapply(
derivs,
function(x){
eval(x)
}
)
# gradient change values
-deriv_vals * lr
}
## get gradient values ----------
progress_list <- list()
for(
i in seq_len(iter_max)
)
{
grad_deltas <- grad_desc_func(lr, curr_list = currs)
currency_vals <- sapply(
currs
, function(x)
{
# update currency values
current_val <- get(x, envir = .GlobalEnv)
new_delta <- grad_deltas[x]
if(new_delta > -1 & new_delta < 1)
{
new_delta = new_delta
} else {
new_delta = sign(new_delta)
}
new_val <- current_val + new_delta
if(new_val > 0 & new_val < 2)
{
new_val = new_val
} else {
new_val = current_val
}
names(new_val) <- NULL
# change values of currencies by gradient descent step in global env
assign(x, new_val , envir = .GlobalEnv)
# save history of values for later plotting
new_val
}
)
progress_list[[i]] <- c(
currency_vals,
eval(express)
)
if(
eval(express) < min_tolerance
)
{
break('solution was found')
}
}
## check results ----------
# print(
# paste0(
# 'Final error: '
# , round(eval(express), 5)
# )
# )
#
# print(
# round(unlist(mget(currs)), 5)
# )
progress_dt <- rbindlist(
lapply(
progress_list
, function(x)
{
as.data.frame(t(x))
}
)
)
colnames(progress_dt)[length(colnames(progress_dt))] <- 'error'
progress_dt[, steps := 1:nrow(progress_dt)]
progress_dt_melt <-
melt(
progress_dt
, id.vars = 'steps'
, measure.vars = colnames(progress_dt)[colnames(progress_dt) != 'steps']
)
progress_dt_melt[, simul := s]
simul_dt <- rbind(
simul_dt
, progress_dt_melt
)
}
ggplot(data = simul_dt) +
facet_wrap(~ variable, scales = 'free') +
geom_line(
aes(
x = steps
, y = value
, group = simul
, color = simul
)
) +
scale_y_log10() +
theme_minimal()
Код на 1000 симуляций работает около минуты.
Заключение
Вот что для меня осталось не понятно:
- можно ли хитрым математическим способом стабилизировать решение;
- будет ли схождение при большем количестве валют и валютных пар;
- если стабильности быть не может, то на каждый новый снэпшот данных наши валюты будут гулять как их вздумается, если не закрепить сид ГПСЧ, а это провал.
Вся затея представляется весьма туманной в отсутствии каких-либо внятных предпосылок и ограничений. Но это было интересно!
Ну, еще хотел сказать, что можно обойтись без МНК, когда данные хитрые, матрицы сингулярные, ну, или, когда теорию плохо знаешь (эхх…).
Спасибо eavprog за изначальный посыл.
Пока!
