Микроспутники для дистанционного зондирования Земли
В настоящее время большой интерес проявляется к созданию и использованию малых космических аппаратов — адекватной замене больших космических аппаратов.
Это объясняется многими преимуществами микроспутников (МС) [1]:
- Сравнительно низкая цена, а также небольшое время, необходимое для разработки и изготовления микроспутника.
- Низкая цена запуска космического аппарата. Ракета-носитель, даже легкого класса, способна вывести на орбиту несколько микроспутников.
- Для запуска применяются конверсионные баллистические ракеты, которые, в соответствии с договорами, уничтожаются путем запуска в космос с полезной нагрузкой.
- Легкие космические аппараты могут выводиться в качестве попутного груза на ракетах-носителях (РН) или в транспортных кораблях, доставляющих грузы на долговременные орбитальные станции.
- Снижение риска больших финансовых потерь при гибели микроспутника в случае аварии РН на старте или при неудачном выведении его на рабочую орбиту.
Микроспутником считается космический аппарат с массой от 10 до 100 кг. Благодаря современному уровню развития науки и техники, на спутнике такого класса можно устанавливать практически все присущие большому космическому аппарату бортовые системы: ориентации (пассивная и активная), электропитания, определения положения, радиосвязи, а также бортовой вычислительный комплекс.
Как сообщает Fast Company, две компании, финская и американская, готовятся запустить целые созвездия недорогих микроспутников, которые многократно увеличат возможности слежения. Низкая стоимость позволит использовать их более широкому кругу клиентов, что внушает беспокойство многим экспертам [2].
Постановка задачи
Анализ возможностей применения двигательной установки по коррекции орбиты микроспутников дистанционного зондирования Земли.
Условия для снабжения микроспутника двигательной установкой.
Микроспутник, пригодный для большинства космических задач, имеет массовые характеристики в пределах 20…70 кг (Lapan TUBSat).
Для данного диапазона масс микроспутника возможно применение двигательной установки, которая легко согласуется по габаритам и составляет 7…25% массы спутника.
При этом двигательная установка должна иметь собственную систему энергоснабжения, контроллер управления, подсистему хранения и подачи топлива с баком емкостью до 3,3 дм3.
Зависимость приращения высоты орбиты от массы спутника
Для решения этой задачи воспользуемся уравнением Циолковского и выражением для расчета характеристической скорости [3]:
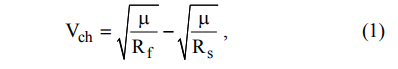
где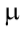 
— гравитационный параметр притягивающего центра (для Земли 
); Rs — радиус начальной орбиты, Rs =6945 км; Rf — радиус конечной орбиты, км.
В результате преобразований, из данных уравнений можно получить следующее выражение:
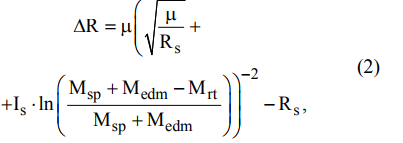
где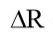 
— приращение высоты орбиты, км; Is — удельный импульс двигателя, Is =12.750 км/с; Msp — масса спутника, кг; Medm — масса двигательной установки, Medm =5,33 кг; Mrt — масса рабочего тела, Mrt =0,73 кг.
import numpy as np
import matplotlib.pyplot as plt
mz=3.986*10**5 # гравитационный параметр притягивающего центра в км3/с2
Rs=6945 #- радиус начальной орбиты в км.
Is=12.750#удельный импульс двигателя км/с
Medm=5.33 # масса двигательной установки в кг.
Mrt=0.73 # масса рабочего тела в кг.
# x - масса спутника в кг.
def dR(x):
return mz*(((mz/Rs)**0.5+Is*np.log((x+Medm-Mrt)/(x+Medm)))**-2)-Rs
p=np.arange(20,50,1)
y=[dR(x) for x in p]
plt.title(' Зависимость приращения высоты орбиты \n от массы спутника ')
plt.ylabel('Приращение высоты орбиты в км.')
plt.xlabel('Масса спутника в кг.')
plt.plot(p,y, color='r',linewidth=2)
plt.grid(True)
plt.show()
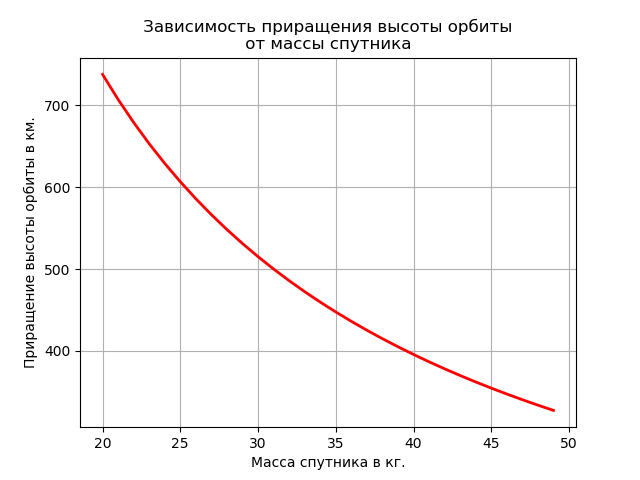
С помощью выражения (2) можно рассчитать максимальное приращение высоты орбиты, которое может обеспечить двигательная установка за суммарное время работы [3]:
где F — тяга двигателя, F =0,0045 Н.
Зависимость времени маневра от промежуточной орбиты
Определим время маневра, которое может понадобиться для поднятия спутника на какую-либо промежуточную орбиту (Rp) в диапазоне от Rs до Rs + .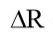
Для расчета времени маневра можно воспользоваться следующим выражением [3]:
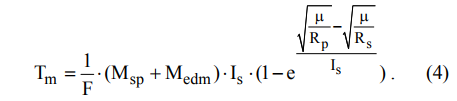
import numpy as np
import matplotlib.pyplot as plt
mz=3.986*10**5 # гравитационный параметр притягивающего центра в км3/с2
Rs=6945 #- радиус начальной орбиты в км.
Is=12.750#удельный импульс двигателя км/с
Medm=5.33 # масса двигательной установки в кг.
Mrt=0.73 # масса рабочего тела в кг.
F =0.0045 #тяга двигательной установки
# xm - масса спутника в кг.
# Rp - промежуточная орбита в км.
def dR(xm,Rp):
m=(np.sqrt(mz/Rp)-np.sqrt(mz/Rs))/Is
return(1/(F*3600))*(xm+Medm)*Is*1000*(1-np.e**m)
p=np.arange(6945,7245,1)
y1=[dR(50,Rp) for Rp in p]
y2=[dR(20,Rp) for Rp in p]
plt.title('Зависимость времени маневра \n от промежуточной орбиты спутника')
plt.ylabel('Время манёвра в час.')
plt.xlabel('Промежуточная орбита в км.')
plt.plot(p,y1, color='r',linewidth=2, label='50 кг.')
plt.plot(p,y2, color='b',linewidth=2, label='20 кг.')
plt.legend(loc='best')
plt.grid(True)
plt.show()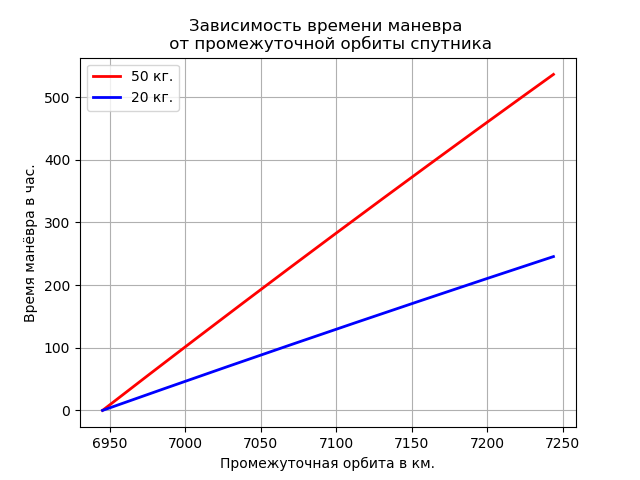
Возможности двигательной установки по изменению плоскости орбиты.
Для расчета изменения наклонения орбиты под воздействием двигателей малых тяг можно воспользоваться следующим выражением [4]:
где V — орбитальная скорость движения, м/c; i — наклонение орбиты; u — аргумент широты спутника. Запишем данное выражение в интегральном виде:
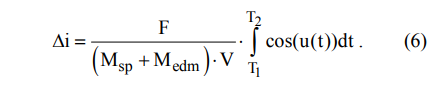
Из данного выражения видно, что для увеличения либо уменьшения наклонения орбиты тяга двигателя должна при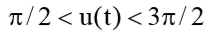 
действовать в одном направлении, а при 
и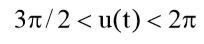 
меняет свое направление на противоположное.
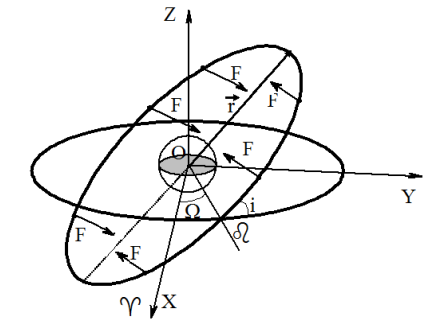
Тяга должна быть перпендикулярна плоскости орбиты. На рисунке показано необходимое направление тяги двигателя в различных точках при увеличении наклонения для орбит с прямым движением.
Выводы
Проведен анализ возможностей применения двигательной установки по коррекции орбиты микроспутников дистанционного зондирования Земли.
- Микроспутники.
- Микроспутники будут круглосуточно следить за любой точкой Земли.
- Балк, М.Б. Элементы динамики космического полета [Текст] / М.Б. Балк. — М.: Наука, 1965. — 339 с.
- Левантовский, В.И. Механика космического полета в элементарном изложении [Текст] / В.И. Левантовский. — М.: Наука, 1974. — 512 с.
