Методы приближенного поиска ближайших соседей
Довольно часто программисты и специалисты из области data science сталкиваются с задачей поиска похожих профилей пользователей или подбора схожей музыки. Решения могут сводиться к преобразованию объектов в векторную форму и поиску ближайших.
Мы тоже столкнулись с необходимостью поиска ближайших соседей в задаче распознавания лиц. Там мы формируем векторные представления лиц при помощи нейросети и ищем ближайшие векторы уже известных людей. Изначально для поиска мы выбрали Annoy, как хорошо известный и проверенный алгоритм, используемый в том числе в Spotify. Но быстро поняли, что с его аппетитами по памяти мы либо не вмещаемся в RAM, либо сильно теряем в точности. Это привело к небольшому исследованию. О результатах которого пойдет речь ниже.
Чтобы разбавить теорию практикой, в статье будет немного кода, где мы ищем ближайших соседей для слов. Получим их векторные представления, используя популярный word2vec. Этот алгоритм выдает близкие векторы для семантически похожих слов. В word2vec CBOW векторные представления получаются как побочный продукт обучения небольшой нейросети, которая предсказывает слово по его окружению. Любопытно, что с векторами можно проворачивать арифметические операции наподобие king + (woman — man) = queen.
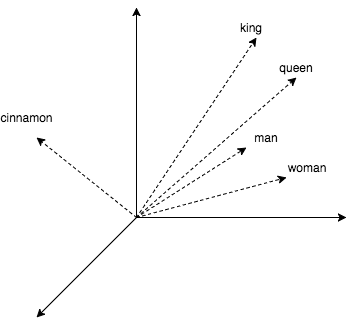
Посмотрим, как с этим работать в коде.
model = gensim.models.KeyedVectors.load_word2vec_format('./GoogleNews-vectors-negative300.bin', binary=True)
start = time.time()
pprint.pprint(model.wv.most_similar(positive=['king']))
print('time:', time.time() - start)
print('king + (woman - man) = ', model.wv.most_similar(positive=['woman', 'king'], negative=['man'])[0])
print('Japan + (Moscow - Russia) = ', model.wv.most_similar(positive=['Moscow', 'Japan'], negative=['Russia'])[0])Получаем:
[(u'kings', 0.7138045430183411),
(u'queen', 0.6510956883430481),
(u'monarch', 0.6413194537162781),
(u'crown_prince', 0.6204219460487366),
(u'prince', 0.6159993410110474),
(u'sultan', 0.5864823460578918),
(u'ruler', 0.5797567367553711),
(u'princes', 0.5646552443504333),
(u'Prince_Paras', 0.5432944297790527),
(u'throne', 0.5422105193138123)]
time: 0.236690998077
king + (woman - man) = (u'queen', 0.7118192911148071)
Japan + (Moscow - Russia) = (u'Tokyo', 0.8696038722991943)В примере выше использовалась библиотека для работы с текстом gensim и word2vec модель (1,5 Гбайт) от Google, которая насчитывает 3 миллиона слов и коротких фраз. В выводе кода видно, что к королю близки королевы, монархи и принцы. Также мы убедились, что арифметика с векторами работает. Однако четверть секунды на один запрос — не очень привлекательно, а ведь в gensim сравнительно хорошая реализация bruteforce-поиска (с подсчетом расстояний до всех известных объектов). Далее мы рассмотрим методы, позволяющие сократить это время в сотни раз лишь с небольшими потерями в точности.
Но начнем с простой идеи: попробуем сузить пространство поиска, разделив его плоскостью на две половины. А во время поиска будем считать расстояния только до тех соседей, которые оказались по ту же сторону от плоскости, что и запрос.
nbrs = NearestNeighbors(algorithm='brute', metric='cosine')
nbrs.fit(model.wv.syn0norm)
king_vec = model.wv['king'][np.newaxis, :]
# замерим скорость поиска сосдей к королю без разделения пространства и заодно выведем результат
start = time.time()
idxs = nbrs.kneighbors(king_vec, return_distance=False, n_neighbors=10)[0]
print('full search time:', time.time() - start)
print([model.wv.index2word[idx] for idx in idxs])
# выберем 2 случайных вектора и получем коэффициенты задающие плоскость между ними
vec1_idx = random.randint(0, model.wv.syn0norm.shape[0])
vec2_idx = random.randint(0, model.wv.syn0norm.shape[0])
plane = model.wv.syn0norm[vec1_idx] - model.wv.syn0norm[vec2_idx]
# в результате следующего умножения матрица-вектор, мы получим вектор.
# Знаки элементов этого вектора указывают с какой стороны разделяющей плоскости оказалось слово
scalar = model.wv.syn0norm.dot(np.transpose(plane))
# определим с какой стороны плоскости запрос и подготовим бинарную маску для выборки векторов по ту же сторону плоскости
if king_vec.dot(plane) > 0:
mask = scalar > 0
else:
mask = scalar < 0
print('elements in mask:', mask.sum())
half_nbrs = NearestNeighbors(algorithm='brute', metric='cosine')
half_nbrs.fit(model.wv.syn0norm[mask])
half_index2word = list(compress(model.wv.index2word, mask))
start = time.time()
idxs = half_nbrs.kneighbors(king_vec, return_distance=False, n_neighbors=10)[0]
print('half search time:', time.time() - start)
print([half_index2word[idx] for idx in idxs])Получаем:
full search time: 20.3163180351
[u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'Prince_Paras']
elements in mask: 1961204
half search time: 9.15824007988
[u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'Prince_Paras']Так мы сократили вычисления вдвое, потеряв в точности только рядом с плоскостью. В кое-каких алгоритмах, которые мы рассмотрим дальше, используются похожие трюки.

1. HNSW
В 2013 году был опубликован один из лучших алгоритмов поиска ближайших соседей Navigable Small World (NSW). В 2016-м появился его наследник Hierarchical Navigable Small World (HNSW).
Начнем с родительского алгоритма NSW. Он основан на графе «мир тесен». Эти графы имеют любопытную и полезную нам особенность: пара вершин с большой вероятностью не смежна, но они достижимы за сравнительно небольшое число шагов ( в среднем). Такие графы встречаются довольно часто. К примеру, нейронные сети мозга, группы в социальных сетях и семантическая сеть WordNet — это графы SW. В нашем случае вершинами являются векторы, а ребра соединяют их с ближайшими. В графе также представлены ребра, соединяющие вершины на большом расстоянии.
Для поиска соседей мы обходим граф в поисках вершин с минимальным расстоянием до запроса. Начинаем со случайной вершины, считаем расстояние от непосещенных вершин «друзей» (вершин, соединенных с текущей ребром) до запроса и переходим в вершину с наименьшим расстоянием. Длинные ребра придают графу свойства тесного мира и позволяют быстро перемещаться в область близких к запросу объектов, а короткие — жадно искать ближайших соседей.
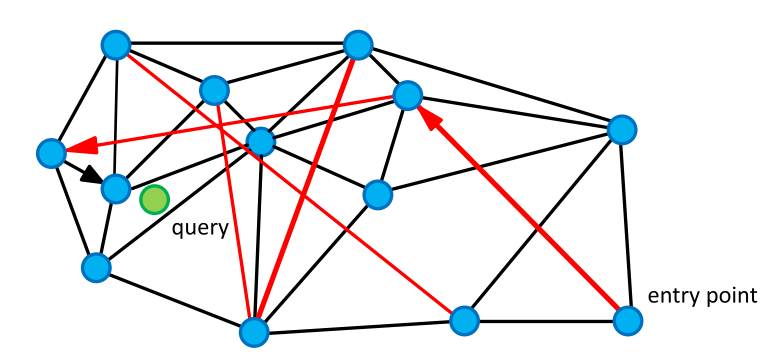
По мере обхода графа обновляем небольшой список ближайших соседей и останавливаемся, если на очередной итерации список не обновился.
K-NNSearch(object q, integer: m, k)
1 TreeSet [object] tempRes, candidates, visitedSet, result
2 for (i←0; i < m; i++) do:
3 put random entry point in candidates
4 tempRes←null
5 repeat:
6 get element c closest from candidates to q
7 remove c from candidates
8 //check stop condition:
9 if c is further than k-th element from result
10 than break repeat
11 //update list of candidates:
12 for every element e from friends of c do:
13 if e is not in visitedSet than
14 add e to visitedSet, candidates, tempRes
15
16 end repeat
17 //aggregate the results:
18 add objects from tempRes to result
19 end for
20 return best k elements from resultindex = nmslib.init(space='cosinesimil', method='sw-graph')
nmslib.addDataPointBatch(index, np.arange(model.wv.syn0.shape[0], dtype=np.int32), model.wv.syn0)
index.createIndex({}, print_progress=True)
start = time.time()
items = nmslib.knnQuery(index, 10, king_vec.tolist())
print(time.time() - start)
print([model.wv.index2word[idx] for idx in items])Получаем:
0.000545024871826
[u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'royal']Рассмотрим развитие описанной выше идеи в алгоритме Hierarchical Navigable Small World (HNSW). Он во многом схож с NSW, однако теперь мы имеем дело с иерархией графов: на нулевом слое представлены все объекты, а по мере увеличения слоя — все меньшая и меньшая их подвыборка. При этом все объекты на слое есть и на слое
.
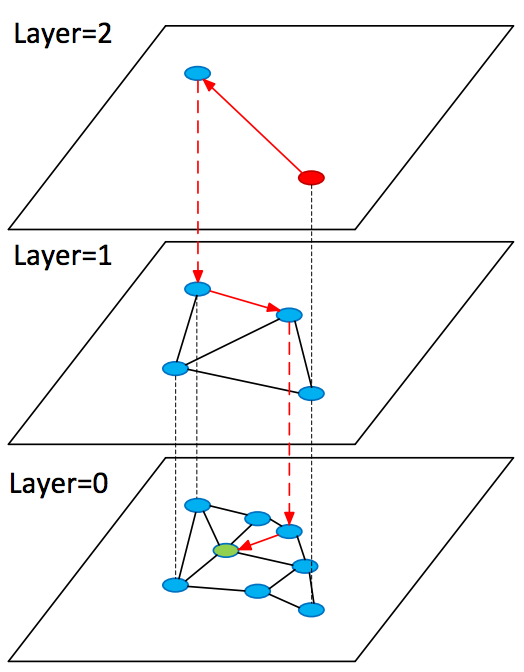
При поиске старт происходит со случайной вершины в графе верхнего слоя, там мы быстро находим близкие к запросу вершины (кандидаты) и возобновляем поиск с них на предыдущем слое.
SearchAtLayer (object q, Set[object] enterPoints, integer: M, ef, layer)
1 Set [object] visitedSet
2 priority_queue [object] candidates (closer - first), result (further - first)
3 candidates, visitedSet, result ← enterPoints
7
4 repeat:
5 object c =candidates.top()
6 candidates.pop()
7 //check stop condition:
8 if d(c,q)>d(result.top(),q) do:
9 break
10 //update list of candidates:
11 for_each object e from c.friends(layer) do:
12 if e is not in visitedSet do:
13 add e to visitedSet
14 if d(e, q)< d(result.top(),q) or result.size()ef do:
17 result.pop()
18 return best k elements from result
K-NNSearch (object query, integer: ef)
1 Set [object] tempRes, enterPoints=[enterpoint]
2 for i=maxLayer downto 1 do:
3 tempRes=SearchAtLayer (query, enterPoints, M, 1, i)
4 enterPoints =closest elements from tempRes
5 tempRes=SearchAtLayer (query, enterPoints, M, ef, 0)
6 return best K of tempRes 1.1. Pros & Cons
+ Алгоритм просто понять
+ Он показывает state-of-the-art результаты
+ Существует эффективная реализация в библиотеке nmslib
+ Небольшие дополнительные расходы памяти на хранение ребер графа
— Алгоритм не поддерживает сжатие векторных представлений, которое мы рассмотрим далее
index = nmslib.init(space='cosinesimil', method='hnsw')
nmslib.addDataPointBatch(index, np.arange(model.wv.syn0.shape[0], dtype=np.int32), model.wv.syn0)
index.createIndex({}, print_progress=True)
start = time.time()
items = nmslib.knnQuery(index, 10, king_vec.tolist())
print(time.time() - start)
print([model.wv.index2word[idx] for idx in items])Получаем:
0.000469923019409
[u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'Prince_Paras']2. FAISS
В марте 2017 года Facebook представила свое решение для ANN — библиотеку FAISS. Она объединяет множество методов и алгоритмов. В алгоритме, который мы рассмотрим ниже, расстояния до групп векторов будут приближаться расстоянием до опорной точки рядом с ними. Так мы можем выяснить расстояния от запроса до небольшого количества опорных точек, а затем полным перебором посчитать расстояния до векторов, принадлежащих опорной точке, которая ближе остальных к запросу. Разберем этот алгоритм по частям.
2.1. ADC — asymmetric distance computation
Рассмотрим подробнее следующую идею: расстояния до групп векторов можно приблизить расстояниями до опорных точек рядом с ними. Опорные точки делят пространство на области. Для поиска опорных точек в FAISS используется широко известный алгоритм кластеризации k-means, векторам сопоставляются полученные центроиды.
(0.1, 0.2) → 1 (0.5, -0.2) → 2 (0.1, 0.1) → 1 (0.6, -0.1) → 2
Векторы коллекции аппроксимируются своими центроидами , где
и
— множество центроидов. Тогда расстояние от запроса
до
может быть приближено
. Такой способ вычисления дистанции называют асимметричным. Простыми словами: мы разбили пространство на области и сказали, что расстояние от запроса до группы векторов, попавших в одну область, приблизительно равно расстоянию до центроида, образующего эту область.

Эффективно хранить и быстро получать векторы, принадлежащие центроиду, помогает простой трюк под названием inverted file.
2.2. IVF — inverted file
В IVF мы инвертируем присвоение. Теперь центроидам сопоставляются списки векторов.
1 → [(0.1, 0.2), (0.1, 0.1)] 2 → [(0.5, -0.2), (0.6, -0.1)]
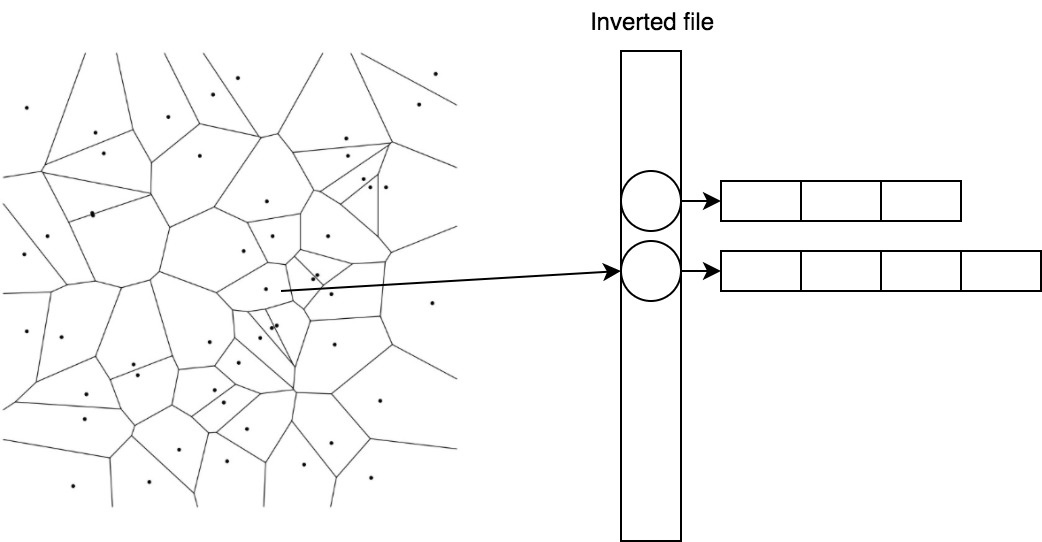
Так мы можем быстро находить кандидатов, посчитав расстояния до центроидов, а затем брать уже готовый список для ближайшего.
2.3. PQ — product quantizer
Последняя составляющая, которой мы коснемся в статье, называется product quantizer. Она обеспечивает сжатие векторов с потерями и применяется, когда векторные представления не влезают в память. Предположим, что наши векторы имеют размерность 128 и мы хотим кодировать их 64 битами (всего 0,5 бита на компоненту), тогда нам придется заниматься квантованием с количеством центроидов, равным . Это нетривиальная задача
, которая также требует огромной обучающей выборки.
Упростим задачу, разбив вектор на частей
, и по традиции найдем 256 центроидов для каждой из частей. То есть вектор можно переписать как набор индексов центроидов — например
, а занимает это хозяйство
байт.
Такой вид кодирования будем применять к остаточным векторам ,
, и тогда
2.4. Поиск
А теперь соберем все это в одной схеме.

Для запроса находим
ближайших центроидов, собираем списки векторов, соответствующих этим центроидам, и считаем до них расстояния, используя остаточные векторы, а затем выбираем
ближайших.
import faiss
index = faiss.index_factory(model.wv.syn0norm.shape[1], 'IVF16384,Flat')
index.verbose = True
train = model.wv.syn0norm[np.random.binomial(1, 1./3, size=model.wv.syn0norm.shape[0]).astype(bool)]
index.train(train)
index.add(model.wv.syn0norm)
index.nprobe = 100
start = time.time()
distances, items = index.search(king_vec, 10)
print(time.time() - start)
print([model.wv.index2word[idx] for idx in items[0]])Получаем:
0.0048999786377
[u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'Prince_Paras']2.5. Pros & Cons
+ Поддержка сжатия
+ Малые накладные расходы на хранение центроидов
+ Возможность вычислений на GPU*
— В пять раз медленнее HNSW на CPU
* Мы не смогли быстро завести GPU-реализацию из коробки и решили не тратить время на это.
3. ANNOY
Идея деления пространства плоскостями хорошо реализована в Annoy. Алгоритм прекрасно описан автором в блоге, рекомендую прочесть, если хотите разобраться в деталях. Я попробую коротко изложить суть. В алгоритме мы рекурсивно делим пространство плоскостями, образуя бинарное дерево. В каждом узле дерева хранится вектор, задающий текущую плоскость. При поиске мы начинаем с корня и выбираем дочернюю ноду на основе положения запроса относительно плоскости. Так мы спускаемся к листовым элементам дерева, в которых хранятся векторы, оказавшиеся по одну сторону группы плоскостей (это небольшой кусочек пространства), они с высокой вероятностью окажутся искомыми ближайшими соседями. Посмотрим на достоинства и недостатки Annoy по сравнению с другими алгоритмами.
3.1. Pros & Cons
+ Алгоритм просто понять
— Он требует много памяти
— Проигрывает в скорости работы
Сравнение алгоритмов
У каждого из алгоритмов есть набор параметров, будь то максимальное количество друзей для вершины (в NSW, HNSW) или количество центроидов (в FAISS). Эти параметры влияют на объем потребляемой памяти, качество и скорость поиска. Автор Annoy реализовал тесты для группы ANN алгоритмов в репозитории ann-benchmarks на разных параметрах. В них оценивается точность поиска десяти ближайших соседей в датасетах, полученных при помощи алгоритмов GloVe и SIFT.
GloVe — это еще один способ получить векторные представления слов, он превосходит word2vec по всем показателям при обучении на корпусе одного размера. Датасет составлен из 1,2 миллиона векторных представлений слов, обученных на 2 миллиардах твитов. SIFT — старый алгоритм получения ключевых точек изображения и их векторных представлений, устойчивых к трансформациям. Он использовался для распознавания объектов, и важной частью этого распознавания был поиск похожих векторных представлений. Есть несколько вариаций датасетов, нас интересует SIFT 1M, содержащий миллион векторов.
Ниже приведу графики, отражающие взаимосвязь скорости работы алгоритмов и точности поиска десяти ближайших соседей. Алгоритмы представлены группами точек, каждая из точек — это запуск теста на наборе параметров.
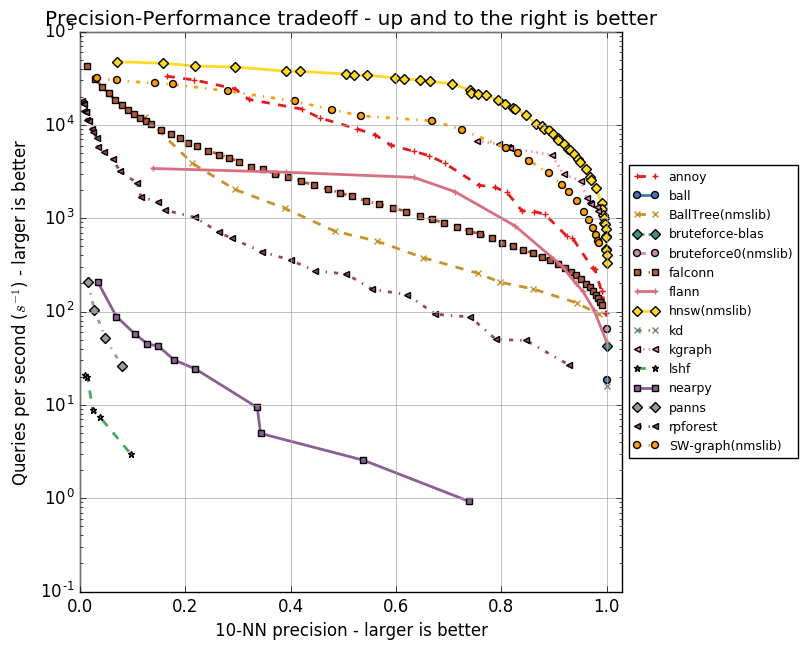
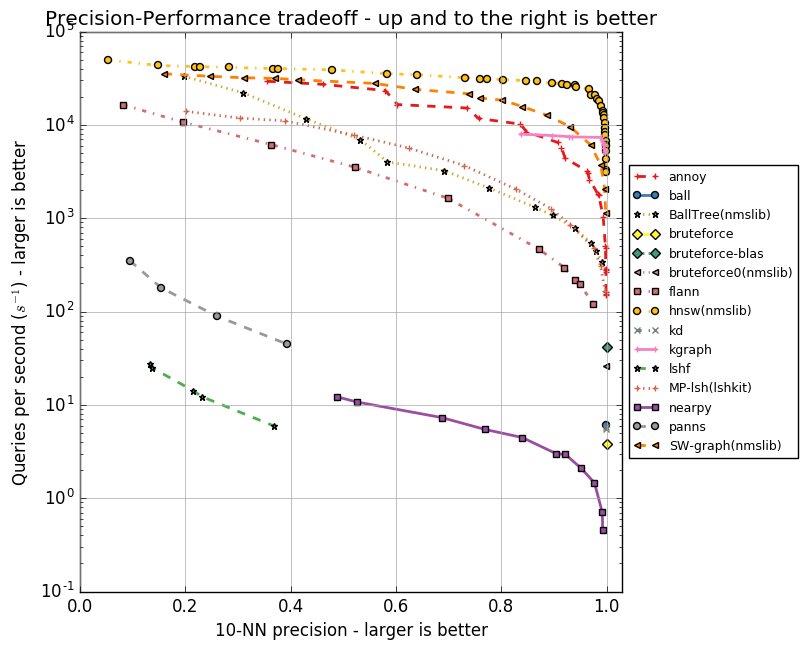
Видно, что HNSW уверенно лидирует. Однако на графиках нет FAISS. Facebook самостоятельно сравнил HNSW и FAISS в разных конфигурациях, результаты приведены в таблице.
| Method | search time | 1-R@1 | index size | index build time |
|---|---|---|---|---|
| Flat-CPU | 9.100 s | 1.0000 | 512 MB | 0 s |
| nmslib (hnsw) | 0.081 s | 0.8195 | 512 + 796 MB | 173 s |
| IVF16384, Flat | 0.538 s | 0.8980 | 512 + 8 MB | 240 s |
| IVF16384, Flat (Titan X) | 0.059 s | 0.8145 | 512 + 8 MB | 5 s |
| Flat-GPU (Titan X) | 0.753 s | 0.9935 | 512 MB | 0 s |
В таблице методы FAISS без сжатия, в частности IVF16384,Flat. Значит, используется IVFADC c 16 384 центроидами. Расходы памяти указаны для случая с миллионом векторов размерности 128 в float32. HNSW в пять раз быстрее при вычислениях на CPU, но на хранение ребер графа () требуется больше памяти, чем на центроиды (
).
4. Заключение
Мы рассмотрели ряд алгоритмов, применяемых для быстрого поиска ближайших соседей. Annoy проиграл и по памяти, и по скорости работы, но идея хороша и может помочь в решении смежных задач. Например, удобный для чистки датасета алгоритм поиска аномалий isolation forest очень похож по своей задумке. FAISS — отличное решение при ограничениях по памяти, с ним вполне можно уложить миллиард векторных представлений в 60 Гбайт RAM, используя IVF16384, PQ64. Однако если память не узкое место, то стоит выбрать HNSW.
P.S. Самыми интересными оказались публикации об алгоритмах в FAISS. Там, к примеру, можно прочесть об оптимизации под GPU, об улучшенном методе квантования (Optimized Product Quantization) и о более хитром способе построении индекса (inverted multi-index).
P.P. S. Для себя мы выбрали HNSW.
5. Литература
- Approximate nearest neighbor algorithm based on navigable small world graphs
- Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs
- Product quantization for nearest neighbor search
- SEARCHING IN ONE BILLION VECTORS: RE-RANK WITH SOURCE CODING
- GloVe: Global Vectors for Word Representation
- Object Recognition from Local Scale-Invariant Features
- Isolation Forest
- Billion-scale similarity search with GPUs
- Optimized Product Quantization
- The inverted multi-index
