Методические заметки об отборе информативных признаков (feature selection)29.06.2016 10:33

Меня зовут Алексей. Я Data Scientist в компании Align Technology. В этом материале я расскажу вам о подходах к feature selection, которые мы практикуем в ходе экспериментов по анализу данных.

В нашей компании статистики и инженеры machine learning анализируют большие объемы клинической информации, связанные с лечением пациентов. В двух словах смысл этой статьи можно свести к извлечению ценных крупиц знания, содержащихся в небольшой доле доступных нам зашумленных и избыточных гигабайтов данных.

Установлено, что наборы с большим количеством входных переменных могут содержать избыточную информацию и ведут к переобученности моделей машинного обучения в том случае, если в модели не встроен регуляризатор. Стадия отбора информативных признаков (ОИП здесь и далее) часто является необходимым шагом в предобработке данных в ходе эксперимента.

• В первой части данной статьи мы сделаем обзор некоторых методов отбора признаков и рассмотрим теоретические моменты в этом процессе. Данный раздел является скорее систематизацией наших взглядов.
• Во второй части статьи на примере искусственного набора данных мы поэкспериментируем с отбором информативных признаков и сделаем сравнение результатов.
• В третьей части мы осветим теорию и практику использования мер из теории информации в применении к обсуждаемой задаче. Метод, представленный в этом разделе, обладает новизной, однако он, по-прежнему, требует проведения многочисленных проверок на различных наборах данных.

Эксперименты, проведенные в статье, не претендуют на научную законченность в силу того, что аналитические обоснования оптимальности того или иного метода приведены не будут, и читатель отсылается к первоисточникам за более подробным и математически точным изложением. Помимо этого, disclaimer состоит в том, что на других данных ценность того или иного метода поменяется, что и делает задачу в целом интеллектуально привлекательной.

В конце статьи будут сведены результаты экспериментов и сделана ссылка на полный код R на Git.

Я выражаю благодарность всем людям, прочитавшим материал до публикации и сделавшим его лучше, в частности, Владу Щербинину и Алексею Селезневу.

1) Способы и методы отбора информативных признаков.

Давайте рассмотрим общий подход к классификации методов ОИП, обратившись к Вики:

Алгоритмы отбора информативных признаков могут быть представлены следующими группами: Wrappers (оберточные), Filters (фильтровочные) и Embedded (встроенные в машины). (Я оставлю без точного перевода эти термины в виду размытости их звучания для русскоязычного сообщества — прим. мое.)

Оберточные алгоритмы создают поднаборы, используя поиск в пространстве возможных входных переменных и оценивают полученные поднаборы входов путем обучения полной модели на имеющихся данных. Оберточные алгоритмы могут быть очень дорогими и рискуют переобучать модель. (Если не используется валидационная выборка — прим. мое.)

Фильтровочные алгоритмы похожи на оберточные в том, что они также выполняют поиск поднаборов входных данных, но, вместо запуска полной модели, важность поднабора для выходной переменной оценивается с помощью более простого (фильтровочного) алгоритма.

Встроенные в машины алгоритмы оценивают важность входных признаков с помощью эвристики, заранее заложенной в обучение.

Источник.

Примеры.

Оберточным алгоритмом ОИП можно назвать комбинацию методов, включающую поиск поднабора входных переменных с последующим обучением, например, random forest, на отобранных данных и оценкой его ошибки на кроссвалидации. То есть для каждой итерации мы будем обучать целую машину (уже фактически готовую к дальнейшему использованию).

Фильтровочным алгоритмом ОИП можно назвать перебор входных переменных, дополняемый проведением статистического теста на зависимость между отобранными переменными и выходом. Если наши входы и выход категориальны, то возможно провести тест хи-квадрат на независимость между входом (или комбинированным набором входов) и выходом с оценкой p-value и, как следствие, бинарным выводом о значимости или незначимости отобранного набора признаков. Другими примерами фильтровочных алгоритмов можно считать:

• линейную корреляцию входа и выхода;
• статистический тест на разницу в средних в случае категориальных входов и непрерывного выхода;
• F-критерий (дисперсионный анализ).

На этом этапе важно понять, что это разграничение, по сути, указывает на различие фитнесс-функций ОИП, то есть меры релевантности найденного поднабора входных признаков по отношению к решаемой задаче. Впоследствии мы еще вернемся к вопросу выбора фитнесс-функции.

Теперь, когда мы немного ориентируемся в основных группах методов ОИП, предлагаю обратить внимание на то, какими методами осуществляется именно перебор поднаборов входных переменных. Снова обратимся к странице Вики:

Подходы к перебору включают:

• Полный перебор
• Первый лучший кандидат
• Имитация отжига
• Генетический алгоритм
• Жадный поиск на включение
• Жадный поиск на исключение
• Particle swarm optimization
• Targeted projection pursuit
• Scatter Search
• Variable Neighborhood Search

Источник.

Я умышленно не стал переводить названия некоторых алгоритмов, так как не знаком с их русскоязычной интерпретацией.

Поиск поднабора предикторов — это дискретная задача, так как на выходе мы получаем вектор целых чисел, обозначающих индексы входов, вида:

входы: 1 2 3 4 5 6… 1000
отбор: 0 0 1 1 1 0… 1

Мы вернемся к этой особенности позднее и проиллюстрируем, к чему она ведет практически.

От того, как будет настроен поиск поднабора входных признаков, сильно зависит результат всего эксперимента. Для того чтобы интуитивно понять основное отличие в этих подходах, я предлагаю читателю поделить их на две группы: жадные (greedy) и нежадные (non-greedy).

Жадные алгоритмы поиска.

Они используются часто, так как быстры и дают хороший результат во многих задачах. Жадность алгоритма заключается в том, что если был выбран (или исключен) один из кандидатов на вхождение в финальный поднабор, в дальнейшем он в нем остается (в случае жадного включения) или навсегда отсутствует (в случае жадного исключения). Таким образом, если на ранних итерациях был выбран кандидат А, на поздних итерациях поднабор всегда будет включать его и других кандидатов, которые вместе с А показывают улучшение метрики важности поднабора для выходной переменной. Обратная ситуация для исключения: если был убран кандидат А, потому что после его исключения метрика важности наименее пострадала или улучшилась, исследователь не получит информации о метрике важности, где в поднаборе есть А и другие, исключенные позже кандидаты.

Если проводить параллель с поиском максимума (минимума) в многомерном пространстве, жадный алгоритм будет застревать в локальном минимуме, если такой есть, либо быстро находить оптимальное решение, если есть единственный минимум, и он глобален.

С другой стороны, перебор всех жадных вариантов осуществляется относительно быстро и позволяет учесть некоторые взаимодействия между входами.

Примеры жадных алгоритмов: жадное включение (forward selection; step forward) и жадное исключение (backward elimination; step backward). На этом список не ограничивается.

Нежадные алгоритмы поиска.

Принцип работы нежадных алгоритмов подразумевает возможность отбросить целиком или частично сформированные поднаборы признаков, комбинации поднаборов между собой и внести случайные изменения в поднаборы с целью избежания локального минимума.

Если провести аналогию с поиском максимума (минимума) значения фитнесс-функции в многомерном пространстве, нежадные алгоритмы рассматривают гораздо больше соседних точек и даже могут совершать большие скачки в случайные области.

Можно представить графически работу этих видов алгоритмов.

Сначала жадное включение:

Теперь нежадный — стохастический — поиск:

В обоих случаях нужно отобрать одну самую лучшую комбинацию из двух входов, чьи индексы отложены по осям графика. Жадный алгоритм начинает с того, что отбирает один лучший вход, перебирая индексы по горизонтали. А затем добавляет к отобранному входу второй вход так, чтобы их суммарная релевантность была максимальна. Но получается, что из все возможных комбинаций он полностью проходит только 1/37 часть. При добавлении еще одного измерения, количество пройденных ячеек станет еще меньше: примерно, 1/37^2.

При этом возможна практическая ситуация, когда лучшей является не та комбинация, которую нашел жадный алгоритм. Это может произойти, если каждый из двух входов по отдельности не показывает лучшую релевантность задаче (и они не будут отобраны на первом шаге), но их взаимодействие максимизирует метрику релевантности.

Нежадный алгоритм ищет гораздо дольше:

(O) = 2^n

и проверяет больше воможных комбинаций входов. Но он имеет шанс найти, возможно, еще более хороший поднабор входов благодаря размашистому поиску сразу во всех изменениях задачи.

Есть алгоритмы поиска, выходящие за рамки установленной дихотомии жадный / нежадный.

Примером такого обособленного поиска будет являться поочередный перебор входов по отдельности и оценка их отдельной важности для выходной переменной. С этого, кстати, начинается первая волна в алгоритме жадного включения переменных. Но что же получается хорошего с таким перебором, за исключением того, что он очень быстрый? Каждая входная переменная начинает существовать «в вакууме», то есть без учета влияния других входов на связь между выбранным входом и выходом. При этом, после завершения работы алгоритма получившийся список входов с указанием их индивидуальной важности для выхода всего лишь дает информацию об индивидуальной значимости каждого предиктора. При объединении некоторого количества самых важных предикторов, согласно такому списку, можно получить ряд проблем:

• избыточность (в случае корреляции предикторов между собой);
• недостаточность информации из-за неучета взаимодействий предикторов на этапе отбора;
• размытость границы, выше которой нужно взять предикторы.

Как можно видеть, проблемы не самые тривиальные.

Основной вопрос в задаче ОИП формулируется как оптимальная комбинация метода поиска поднабора и фитнесс-функции.

Рассмотрим подробнее это утверждение. Наша задача ОИП может быть описана двумя гипотезами:

а) поверхность ошибки простая или сложная;
б) в данных есть простые зависимости или сложные.

В зависимости от ответов на эти вопросы следует остановить выбор на конкретной связке метода поиска и метода определения релевантности отобранных признаков.

Поверхность ошибки.

Пример несложной поверхности: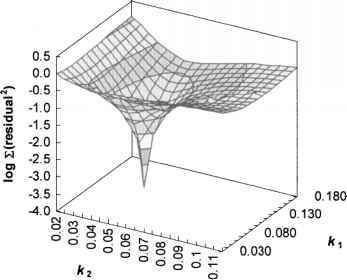

Источник.

Здесь мы выбираем комбинацию из двух входов, определяя их релевантность выходу и спускаемся по плавной поверхности в направлении градиента, почти наверное попадая в точку оптимума.

Пример сложной поверхности:

Источник.

В этом случае, решая ту же задачу, мы встречаемся с множеством локальных минимумов, выбраться из которых жадный алгоритм не сможет. В то же время, алгоритм со стохастическим поиском имеем повышенный шанс найти более точное решение.

Ранее мы упомянули, что поиск поднабора предикторов — это дискретная задача. Если зависимость выхода от входов включает в себя взаимодействия, при при переходе из одной точки пространства в соседнюю можно наблюдать резкие скачки значения фитнесс-функции. Поверхность ошибки в нашем случае часто не гладкая, не дифференцируемая: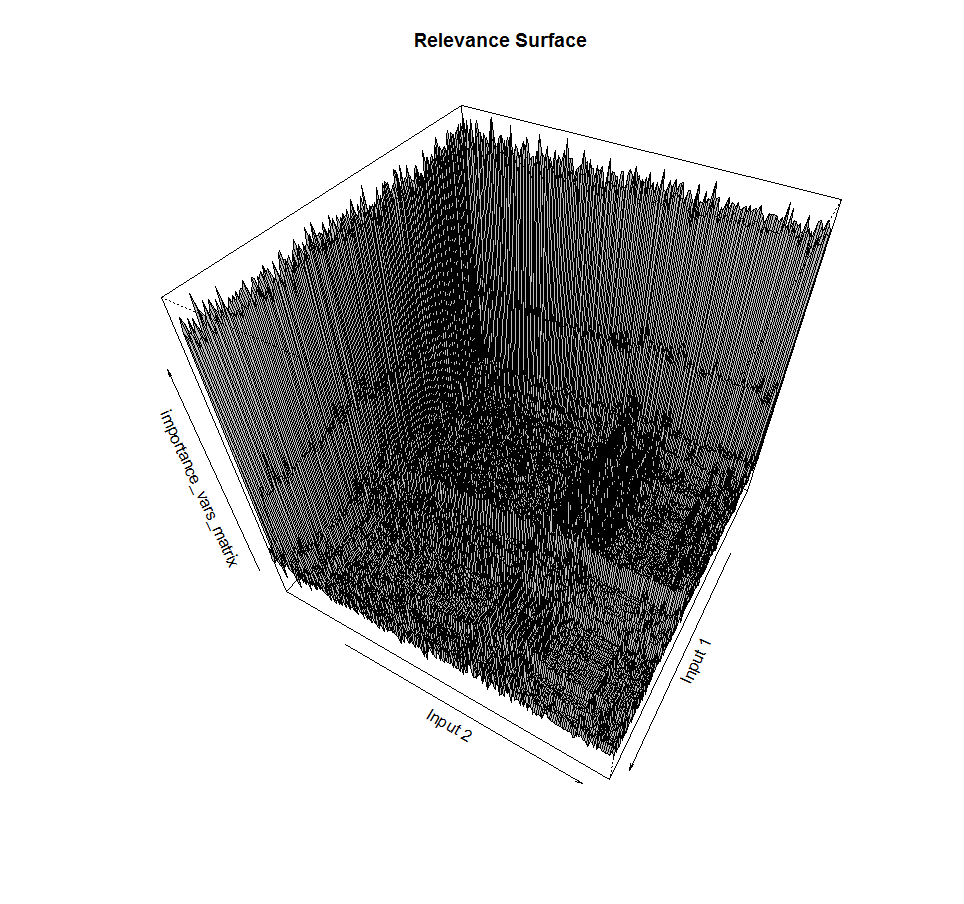

Это пример поиска поднабора из двух входов и соответствующее значение функции релевантности поднабора выходной переменной. Видно, что поверхность далеко не гладкая, с пиками, а также включает в себя изрезанные плато примерно одинаковых значений. Ночной кошмар для методов жадного градиентного спуска.

Зависимости.

С ростом числа измерений задачи повышается теоретичекий шанс того, что зависимость выходной переменной имеет весьма сложную структуру и задействует множество входов. Кроме того, завимость может иметь как линейный вид, так и быть нелинейной. Если зависимость подразумевает взаимодействие предикторов и нелинейный вид, найти ее можно будет, только учитывая оба эти момента, применив, например, обучение random forest или нейронную сеть. Если зависимость простая, линейная, включает в себя только небольшую часть из всех предикторов, подход к ее нахождению — и, как следствие, к ОИП, — можно свести к поочередному включению в модель линейной регрессии по 1 или несколько входов с оценкой качества модели.

Пример простой зависимости: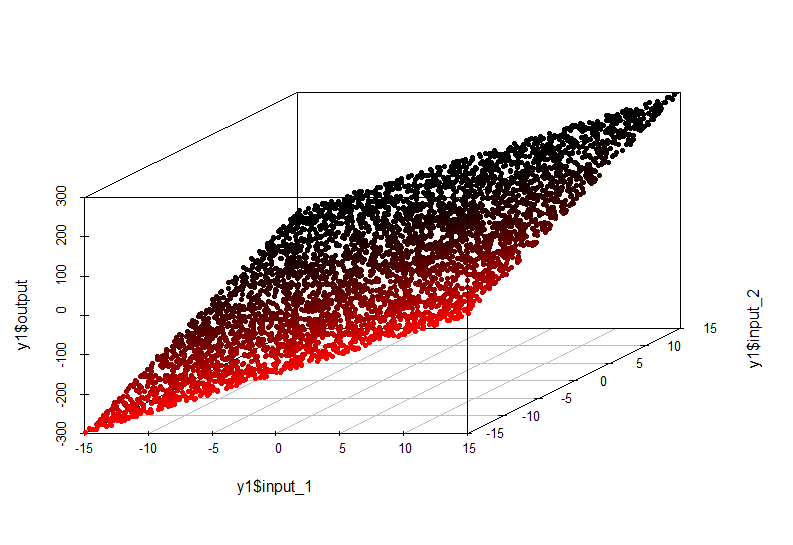

В данном случае зависимость значения по оси output от значений input1 и input2 описывается плоскостью в пространстве:

output = input1×10 + input2×10

Пример сложной зависимости: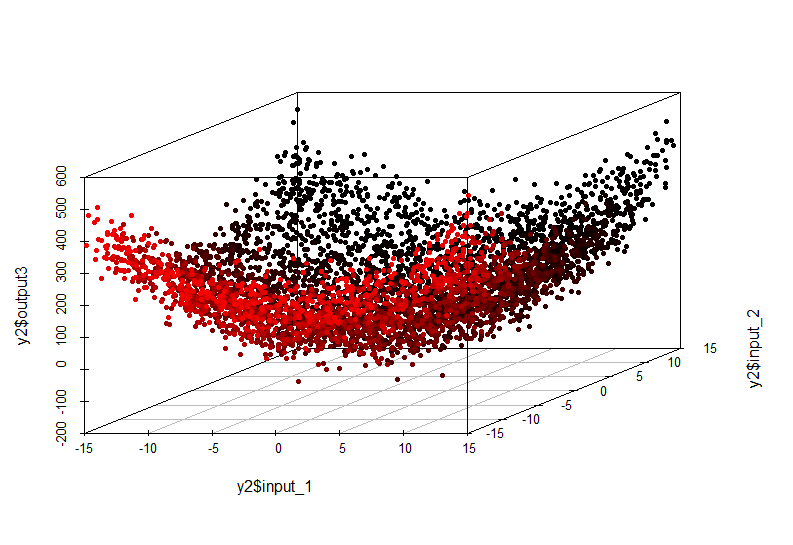

Эта нелинейная зависимость уже не может быть выявлена построением линейной модели. Ее вид таков:

output = input1^2 + input2^2

Также необходимо учесть размерность задачи.

Если количество входных переменных велико, поиск оптимального поднабора стохастическими методами (нежадными) может быть очень дорогим в силу того, что общее количество всех возможных поднаборов задается отношением

m = 2 ^ n,
где n — количество всех входных признаков.

Соответственно, поиск минимума в таком многообразии может быть очень долог. С другой стороны, применение жадного поиска позволит сделать первое приближение за разумное время, даже если это будет локальным минимумом и исследователь будет знать об этом.

В условиях отсутствия предметного знания об изучаемом явлении невозможно заранее сказать, насколько сложной будет зависимость входных переменных и выхода и какое количество входов будет оптимально для нахождения приближенного или точного решения задачи отбора оптимального поднабора входов. Также затруднительно предсказать, будет ли поверхность ошибки при ОИП гладкой и простой или сложной и изрезанной.

Также мы всегда ограничены в ресурсах и должны принимать наиболее оптимальные решения. В качестве небольшой помощи при выработке подхода к ОИП можно использовать следующую таблицу:

Таким образом, у нас всегда есть возможность рассмотреть несколько комбинаций методов поиска поднабора входов и фитнесс-функции релевантности. Самая дорогая и, наверное, наиболее эффективная комбинация — это жадный поиск и оберточная (wrapper) фитнесс-фукнция. Позволяет избегать локального минимума, при этом предоставляя наиболее точную меру релевантности отобранных входов, так как на каждой итерации есть обученная модель (и ее точность на валидации).

Наименее дорогой, но не всегда наимее эффективный подход, это жадный поиск в паре с фильтровочной (filter) функцией, которая может быть статистическим тестом, коэффициентом корреляции или количеством взаимной информации.

Кроме того, встроенные (embedded) методы позволяют сразу после обучения модели отсеять ряд ненужных с точки зрения алгоритма входов, не потеряв существенно в точности моделирования.

Хорошим тоном будет попытка несколько раз решить задачу разными способами и выбрать наилучший.

В общем говоря, отбор информативных признаков — это подбор лучшей комбинации метода поиска в многомерном пространстве и наиболее оптимальной фитнесс-функции релевантности отобранного поднабора по отношению к выходной переменной.

Источник.

2) Эксперименты по отбору информативных признаков на синтетических данных.

Наш подопытный набор данных («Стэнфордский кролик»):

Просто я люблю кроликов.

Мы будем смотреть на зависимость высоты точки (ось Z) от широты и долготы. При этом в набор я добавляю 10 шумовых переменных с распределением примерно соответствующим смеси двух информативных входов (X и Y), но никак не связанных с переменной Z.

Посмотрим на гистограммы плотности распределения для переменных X, Y, Z и одной из шумовых переменных.

Видно, что распределения с произвольными параметрами. При этом все шумовые переменные распределены так, что у них есть небольшой пик в некоторой области значений.

Далее набор данных будет случайно поделен на две части: обучение и валидация.

Подготовка данных.

library(onion)
data(bunny)

#XYZ point plot
open3d()
points3d(bunny, col=8, size=0.1)

bunny_dat <- as.data.frame(bunny)

inputs <- append(as.numeric(bunny_dat$x),
		   as.numeric(bunny_dat$y))

for (i in 1:10){
	
	naming <- paste('input_noise_', i, sep = '')
	bunny_dat[, eval(naming)] <- inputs[sample(length(inputs), nrow(bunny_dat), replace = T)]
	
	
}

Эксперимент №1: жадный поиск поднабора входов с линейной функцией оценки важности (в качестве фитнесс-функции будет использоваться вариант wrapper — оценка коэффициента детерминации обученной модели на валидационной выборке).

### greedy search with filter function

library(FSelector)

sampleA <- bunny_dat[sample(nrow(bunny_dat), nrow(bunny_dat) / 2, replace = F), c("x",
			    "y",
			    "input_noise_1",  
			    "input_noise_2",
			    "input_noise_3",
			    "input_noise_4",
			    "input_noise_5",
			    "input_noise_6", 
			    "input_noise_7",
			    "input_noise_8",
			    "input_noise_9",
			    "input_noise_10",
			    "z")]

sampleB <- bunny_dat[!row.names(bunny_dat) %in% rownames(sampleA), c("x",
				  "y",
				  "input_noise_1",  
				  "input_noise_2",
				  "input_noise_3",
				  "input_noise_4",
				  "input_noise_5",
				  "input_noise_6", 
				  "input_noise_7",
				  "input_noise_8",
				  "input_noise_9",
				  "input_noise_10",
				  "z")]

linear_fit <- function(subset){
	dat <- sampleA[, c(subset, "z")]
	
	lm_m <- lm(formula = z ~.,
		    data = dat,
		    model = T)
	
	lm_predict <- predict(lm_m,
				 newdata = sampleB)
	
	r_sq_validate <- 1 - sum((sampleB$z - lm_predict) ^ 2) / sum((sampleB$z - mean(sampleB$z)) ^ 2)
	
	print(subset)
	print(r_sq_validate)
	return(r_sq_validate)
}

#subset <- backward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit)
subset <- forward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit)

Результат:

> subset
[1] "x"             "y"             "input_noise_2" "input_noise_5" "input_noise_6" "input_noise_8" "input_noise_9"

Оказались включены шумовые переменные.

Посмотрим на обученную модель:

> summary(lm_m)

Call:
lm(formula = z ~ ., data = dat, model = T)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.060613 -0.022650 -0.000173  0.024939  0.048544 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)    0.0232453  0.0005581  41.651  < 2e-16 ***
x             -0.0257686  0.0052998  -4.862 1.17e-06 ***
y             -0.1572786  0.0052585 -29.910  < 2e-16 ***
input_noise_2 -0.0017249  0.0027680  -0.623    0.533    
input_noise_5 -0.0027391  0.0027848  -0.984    0.325    
input_noise_6  0.0032417  0.0027907   1.162    0.245    
input_noise_8  0.0044998  0.0027723   1.623    0.105    
input_noise_9  0.0006839  0.0027808   0.246    0.806    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.02742 on 17965 degrees of freedom
Multiple R-squared:  0.04937,	Adjusted R-squared:  0.049 
F-statistic: 133.3 on 7 and 17965 DF,  p-value: < 2.2e-16

Видим, что на самом деле статистическую значимость принимают только наши оригинальные входы и свободный член уравнения.

А теперь проведем жадное исключение переменных.

subset <- backward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit)
#subset <- forward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit)

Результат:

> subset
[1] "x"             "y"             "input_noise_2" "input_noise_5" "input_noise_6" "input_noise_8" "input_noise_9"

Модель также включила шумы.

Посмотрим на обученную модель:

> summary(lm_m)

Call:
lm(formula = z ~ ., data = dat, model = T)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.060613 -0.022650 -0.000173  0.024939  0.048544 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)    0.0232453  0.0005581  41.651  < 2e-16 ***
x             -0.0257686  0.0052998  -4.862 1.17e-06 ***
y             -0.1572786  0.0052585 -29.910  < 2e-16 ***
input_noise_2 -0.0017249  0.0027680  -0.623    0.533    
input_noise_5 -0.0027391  0.0027848  -0.984    0.325    
input_noise_6  0.0032417  0.0027907   1.162    0.245    
input_noise_8  0.0044998  0.0027723   1.623    0.105    
input_noise_9  0.0006839  0.0027808   0.246    0.806    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.02742 on 17965 degrees of freedom
Multiple R-squared:  0.04937,	Adjusted R-squared:  0.049 
F-statistic: 133.3 on 7 and 17965 DF,  p-value: < 2.2e-16

Аналогично, внутри модели видим, что важны только оригинальные входы.

Если же мы обучим модель только на переменных X и Y, мы получим:

> print(subset)
[1] "x" "y"
> 	print(r_sq_validate)
[1] 0.05185492

> summary(lm_m)

Call:
lm(formula = z ~ ., data = dat, model = T)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.059884 -0.022653 -0.000209  0.024955  0.048238 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.0233808  0.0005129  45.590  < 2e-16 ***
x           -0.0257813  0.0052995  -4.865 1.15e-06 ***
y           -0.1573098  0.0052576 -29.920  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.02742 on 17970 degrees of freedom
Multiple R-squared:  0.04908,	Adjusted R-squared:  0.04898 
F-statistic: 463.8 on 2 and 17970 DF,  p-value: < 2.2e-16

Дело в том, что на валидации R^2 был повыше тогда, когда выключены шумовые переменные.

Странный результат! Наверное, из-за структуры данных шумы не оказывают пагубного влияния на модель.

Но мы еще не попробовали учесть взаимодействие предикторов.

lm_m <- lm(formula = z ~ x * y,
		    data = dat,
		    model = T)

> summary(lm_m)

Call:
lm(formula = z ~ x * y, data = dat, model = T)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.057761 -0.023067 -0.000119  0.024762  0.049747 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.0196766  0.0006545  30.062   <2e-16 ***
x           -0.1513484  0.0148113 -10.218   <2e-16 ***
y           -0.1084295  0.0075183 -14.422   <2e-16 ***
x:y          1.3771299  0.1517363   9.076   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.02736 on 17969 degrees of freedom
Multiple R-squared:  0.05342,	Adjusted R-squared:  0.05327 
F-statistic: 338.1 on 3 and 17969 DF,  p-value: < 2.2e-16

Получилось неплохо. Взамодействие X и Y значимо. А что насчет R^2 на валидации?

> lm_predict <- predict(lm_m,
+ 				 newdata = sampleB)
> 1 - sum((sampleB$z - lm_predict) ^ 2) / sum((sampleB$z - mean(sampleB$z)) ^ 2)
[1] 0.05464066

Это самое высокое значение, из тех, что мы видели. К сожалению, именно вариант взаимодействия не был заложен в фитнесс-функцию и мы пропустили эту комбинацию входов.

Эксперимент №2: жадный поиск поднабора входов с линейной функцией оценки важности (в качестве фитнесс-функции будет использоваться вариант embedded — f-статистика обученной модели на обучающей выборке).

linear_fit_f <- function(subset){
	dat <- sampleA[, c(subset, "z")]
	
	lm_m <- lm(formula = z ~.,
		    data = dat,
		    model = T)
	
	print(subset)
	print(summary(lm_m)$fstatistic[[1]])
	return(summary(lm_m)$fstatistic[[1]])
}

#subset <- backward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit_f)
subset <- forward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit_f)

Результат последовательного включения переменных — только один предиктор Y. Для него максимизировалась F-Statistic. То есть это переменная очень важна. Но почему-то забыта переменная X.

А теперь последовательное исключение переменных.

Результат аналогичен — только одна переменная Y.

Можно отметить, что при максимизации F-Statistic многопеременной модели все шумы оказались за бортом, и модель при этом получилась робастной: на валидации коэффициент детерминации почти не уступает лучшей модели из эксперимента №1:

> r_sq_validate
[1] 0.05034534

Эксперимент №3: поочередная оценка индивидуальной значимости предикторов с помощью коэффициент корреляции Пирсона (этот вариант наиболее простой, он не учитывает взаимодействия, фитнесс-функция также простая — оценивает только линейную связь).

correlation_arr <- data.frame()

for (i in 1:12){
	
	correlation_arr[i, 1] <- colnames(sampleA)[i]
	correlation_arr[i, 2] <- cor(sampleA[, i], sampleA[, 'z'])
	
}

Результат:

> correlation_arr
               V1            V2
1               x  0.0413782832
2               y -0.2187061876
3   input_noise_1 -0.0097719425
4   input_noise_2 -0.0019297383
5   input_noise_3  0.0002143946
6   input_noise_4 -0.0142325764
7   input_noise_5 -0.0048206943
8   input_noise_6  0.0090877674
9   input_noise_7 -0.0152897433
10  input_noise_8  0.0143477495
11  input_noise_9  0.0027560459
12 input_noise_10 -0.0079526578

Наибольшая корреляция Z с Y, и на втором месте — X. Однако корреляция X не явно выражена и требует проведение статистического теста на значимость отличия коэффициента корреляции от нуля для каждой из переменных.

С другой стороны, во всех проведенных 3-х экспериментах мы вообще не учитывали взаимодействие предикторов (X * Y). Этим можно объяснить то, что оценка единичной значимости или линейное включение предикторов в уравнение не дает нам однозначного ответа.

Такой экспериментик:

> cor(sampleA$x * sampleA$y, sampleA$z)
[1] 0.1211382

Показывает, что взаимодействие X и Y коррелирует с Z довольно сильно.

Эксперимент №4: оценка важности предикторов встроенным в машину алгоритмом (вариант жадного поиска и embedded фитнесс-функции важности входов в GBM).

Обучим Gradient Boosted Trees (gbm) и посмотрим на важность переменных. Хорошая статья, детально описывающая аспекты применения GBM: Gradient boosting machines, a tutorial.

Возьмем параметры обучения с потолка, установим очень низкую скорость обучения, чтобы избежать сильного переобучения. Заметим, что любые деревья решений жадны, а улучшение модели путем добавления многих моделей достигается сэмплированием наблюдений и входов.

library(gbm)

gbm_dat <- bunny_dat[, c("x",
		     "y",
		     "input_noise_1",  
		     "input_noise_2",
		     "input_noise_3",
		     "input_noise_4",
		     "input_noise_5",
		     "input_noise_6", 
		     "input_noise_7",
		     "input_noise_8",
		     "input_noise_9",
		     "input_noise_10",
		     "z")]

gbm_fit <- gbm(formula = z ~.,
		 distribution = "gaussian",
		 data = gbm_dat,
		 n.trees = 500,
		 interaction.depth = 12,
		 n.minobsinnode = 100,
		 shrinkage = 0.0001,
		 bag.fraction = 0.9,
		 train.fraction = 0.7,
		 n.cores = 6)

gbm.perf(object = gbm_fit, 
	  plot.it = TRUE, 
	  oobag.curve = F, 
	  overlay = TRUE)

summary(gbm_fit)

Результат:

> summary(gbm_fit)
                          var rel.inf
y                           y 69.7919
x                           x 30.2081
input_noise_1   input_noise_1  0.0000
input_noise_2   input_noise_2  0.0000
input_noise_3   input_noise_3  0.0000
input_noise_4   input_noise_4  0.0000
input_noise_5   input_noise_5  0.0000
input_noise_6   input_noise_6  0.0000
input_noise_7   input_noise_7  0.0000
input_noise_8   input_noise_8  0.0000
input_noise_9   input_noise_9  0.0000
input_noise_10 input_noise_10  0.0000

Этот подход великолепно справился с поставленной задачей и выделил нешумовые входы, сделав все остальные входы абсолютно незначимыми.

Причем, нужно заметить, что настройка данного эксперимента очень быстрая, все работает практически «из коробки». Более тщательное планирование данного эксперимента, включая кроссвалидацию для получения оптимальных параметров обучения, — дело более сложное, но при подготовке реальной модели в production сделать это необходимо.

Эксперимент №5: оценка важности предикторов, используя стохастический поиск с линейной функцией оценки важности (это нежадный поиск в пространстве входов, а в качестве фитнесс-функции будет использоваться вариант wrapper — оценка коэффициента детерминации обученной модели на валидационной выборке).

В этот раз обучающаяся линейная модель включает попарные взаимодействия между предикторами.

### simulated annealing search with linear model interactions stats

library(scales)
library(GenSA)

sampleA <- bunny_dat[sample(nrow(bunny_dat), nrow(bunny_dat) / 2, replace = F), c("x",
											     "y",
											     "input_noise_1",  
											     "input_noise_2",
											     "input_noise_3",
											     "input_noise_4",
											     "input_noise_5",
											     "input_noise_6", 
											     "input_noise_7",
											     "input_noise_8",
											     "input_noise_9",
											     "input_noise_10",
											     "z")]

sampleB <- bunny_dat[!row.names(bunny_dat) %in% rownames(sampleA), c("x",
									      "y",
									      "input_noise_1",  
									      "input_noise_2",
									      "input_noise_3",
									      "input_noise_4",
									      "input_noise_5",
									      "input_noise_6", 
									      "input_noise_7",
									      "input_noise_8",
									      "input_noise_9",
									      "input_noise_10",
									      "z")]

#calculate parameters
predictor_number <- dim(sampleA)[2] - 1
sample_size <- dim(sampleA)[1]
par_v <- runif(predictor_number, min = 0, max = 1)
par_low <- rep(0, times = predictor_number)
par_upp <- rep(1, times = predictor_number)


############### the fitness function
sa_fit_f <- function(par){
	
	indexes <- c(1:predictor_number)
	
	for (i in 1:predictor_number){
		if (par[i] >= threshold) {
			indexes[i] <- i
		} else {
			indexes[i] <- 0
		}
	}
	
	local_predictor_number <- 0
	for (i in 1:predictor_number){
		if (indexes[i] > 0) {
			local_predictor_number <- local_predictor_number + 1
		}
	}
	
	if (local_predictor_number > 0) {
		
		sampleAf <- as.data.frame(sampleA[, c(indexes[], dim(sampleA)[2])])
		
		lm_m <- lm(formula = z ~ .^2,
			    data = sampleAf,
			    model = T)
		
		lm_predict <- predict(lm_m,
					 newdata = sampleB)
		
		r_sq_validate <- 1 - sum((sampleB$z - lm_predict) ^ 2) / sum((sampleB$z - mean(sampleB$z)) ^ 2)

	} else  {
		r_sq_validate <- 0
	}

	return(-r_sq_validate)
}


#stimating threshold for variable inclusion

threshold <- 0.5 # do it simply

#run feature selection

start <- Sys.time()

sao <- GenSA(par = par_v, fn = sa_fit_f, lower = par_low, upper = par_upp
	      , control = list(
	      	#maxit = 10
	      	max.time = 300
	      	, smooth = F
	      	, simple.function = F))

trace_ff <- data.frame(sao$trace)$function.value
plot(trace_ff, type = "l")
percent(- sao$value)
final_vector <- c((sao$par >= threshold), T)
names(sampleA)[final_vector]
final_sample <- as.data.frame(sampleA[, final_vector])

Sys.time() - start


# check model
lm_m <- lm(formula = z ~ .^2,
	    data = sampleA[, final_vector],
	    model = T)

summary(lm_m)

Что-же получилось?

[1] "5.53%"
> final_vector <- c((sao$par >= threshold), T)
> names(sampleA)[final_vector]
[1] "x"             "y"             "input_noise_7" "input_noise_8" "input_noise_9" "z" 

> summary(lm_m)

Call:
lm(formula = z ~ .^2, data = sampleA[, final_vector], model = T)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.058691 -0.023202 -0.000276  0.024953  0.050618 

Coefficients:
                              Estimate Std. Error t value Pr(>|t|)    
(Intercept)                  0.0197777  0.0007776  25.434   <2e-16 ***
x                           -0.1547889  0.0154268 -10.034   <2e-16 ***
y                           -0.1148349  0.0085787 -13.386   <2e-16 ***
input_noise_7               -0.0102894  0.0071871  -1.432    0.152    
input_noise_8               -0.0013928  0.0071508  -0.195    0.846    
input_noise_9                0.0026736  0.0071910   0.372    0.710    
x:y                          1.3098676  0.1515268   8.644   <2e-16 ***
x:input_noise_7              0.0352997  0.0709842   0.497    0.619    
x:input_noise_8              0.0653103  0.0714883   0.914    0.361    
x:input_noise_9              0.0459939  0.0716704   0.642    0.521    
y:input_noise_7              0.0512392  0.0710949   0.721    0.471    
y:input_noise_8              0.0563148  0.0707809   0.796    0.426    
y:input_noise_9             -0.0085022  0.0710267  -0.120    0.905    
input_noise_7:input_noise_8  0.0129156  0.0374855   0.345    0.730    
input_noise_7:input_noise_9  0.0519535  0.0376869   1.379    0.168    
input_noise_8:input_noise_9  0.0128397  0.0379640   0.338    0.735    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0274 on 17957 degrees of freedom
Multiple R-squared:  0.05356,	Adjusted R-squared:  0.05277 
F-statistic: 67.75 on 15 and 17957 DF,  p-value: < 2.2e-16

Видно, что мы промахиваемся. Включены шумы.

Как видим, лучшее значение коэффициента детерминации на валидации достигнут с включением шумовых переменных. При этом сходимость алгоритма поиска исчерпывающая:

Попробуем поменять фитнесс-функцию, сохраним метод поиска.

Эксперимент №6: оценка важности предикторов, используя стохастический поиск с линейной функцией оценки важности (это нежадный поиск в пространстве входов, фитнесс-функция — embedded p-values, соответствующие коэффициентам модели).

Мы будем отбирать такой набор предикторов, у которых минимизируется среднее значение p-value у входящих в модель коэффициентов.

# fittness based on p-values
sa_fit_f2 <- function(par){
	
	indexes <- c(1:predictor_number)
	
	for (i in 1:predictor_number){
		if (par[i] >= threshold) {
			indexes[i] <- i
		} else {
			indexes[i] <- 0
		}
	}
	
	local_predictor_number <- 0
	for (i in 1:predictor_number){
		if (indexes[i] > 0) {
			local_predictor_number <- local_predictor_number + 1
		}
	}
	
	if (local_predictor_number > 0) {
		
		sampleAf <- as.data.frame(sampleA[, c(indexes[], dim(sampleA)[2])])
		
		lm_m <- lm(formula = z ~ .^2,
			    data = sampleAf,
			    model = T)
		
		mean_val <- mean(summary(lm_m)$coefficients[, 4])
		
	} else  {
		mean_val <- 1
	}
	
	return(mean_val)
}


#stimating threshold for variable inclusion

threshold <- 0.5 # do it simply

#run feature selection

start <- Sys.time()

sao <- GenSA(par = par_v, fn = sa_fit_f2, lower = par_low, upper = par_upp
	      , control = list(
	      	#maxit = 10
	      	max.time = 60
	      	, smooth = F
	      	, simple.function = F))

trace_ff <- data.frame(sao$trace)$function.value
plot(trace_ff, type = "l")
percent(- sao$value)
final_vector <- c((sao$par >= threshold), T)
names(sampleA)[final_vector]
final_sample <- as.data.frame(sampleA[, final_vector])

Sys.time() - start

Результат:

> percent(- sao$value)
[1] "-4.7e-208%"
> final_vector <- c((sao$par >= threshold), T)
> names(sampleA)[final_vector]
[1] "y" "z"

В этот раз все получилось. Были отобраны только оригинальные предикторы, так как их p-values действительно малы.

Сходимость алгоритма хорошая за 60 секунд:

Эксперимент №7: оценка важности предикторов, используя жадный поиск с оценкой важности по качеству обученной модели (это жадный поиск в пространстве входов, фитнесс-функция — wrapper, соответствующий коэффициенту детерминации на валидации модели boosted decision trees).

### greedy search with wrapper GBM validation fitness

library(FSelector)
library(gbm)

sampleA <- bunny_dat[sample(nrow(bunny_dat), nrow(bunny_dat) / 2, replace = F), c("x",
											     "y",
											     "input_noise_1",  
											     "input_noise_2",
											     "input_noise_3",
											     "input_noise_4",
											     "input_noise_5",
											     "input_noise_6", 
											     "input_noise_7",
											     "input_noise_8",
											     "input_noise_9",
											     "input_noise_10",
											     "z")]

sampleB <- bunny_dat[!row.names(bunny_dat) %in% rownames(sampleA), c("x",
									      "y",
									      "input_noise_1",  
									      "input_noise_2",
									      "input_noise_3",
									      "input_noise_4",
									      "input_noise_5",
									      "input_noise_6", 
									      "input_noise_7",
									      "input_noise_8",
									      "input_noise_9",
									      "input_noise_10",
									      "z")]

gbm_fit <- function(subset){
	dat <- sampleA[, c(subset, "z")]
	
	gbm_fit <- gbm(formula = z ~.,
			 distribution = "gaussian",
			 data = dat,
			 n.trees = 50,
			 interaction.depth = 10,
			 n.minobsinnode = 100,
			 shrinkage = 0.1,
			 bag.fraction = 0.9,
			 train.fraction = 1,
			 n.cores = 7)
	
	gbm_predict <- predict(gbm_fit,
				 newdata = sampleB,
				 n.trees = 50)
	
	r_sq_validate <- 1 - sum((sampleB$z - gbm_predict) ^ 2) / sum((sampleB$z - mean(sampleB$z)) ^ 2)
	
	print(subset)
	print(r_sq_validate)
	return(r_sq_validate)
}

subset <- backward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = gbm_fit)
subset <- forward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = gbm_fit)

Результат при жадном включении предикторов:

> subset
[1] "x" "y"

> r_sq_validate
[1] 0.2363794

Попали в точку!

Результат при жадном исключении предикторов:

> subset
 [1] "x"              "y"              "input_noise_1"  "input_noise_2"  "input_noise_3"  "input_noise_4"  "input_noise_5"  "input_noise_6"  "input_noise_7" 
[10] "input_noise_9"  "input_noise_10"

> r_sq_validate
[1] 0.2266737

Тут все хуже. Включение шумовых предикторов в модель не сильно ухудшило качество предсказания на валидации. И этому есть объяснение: случайные леса решений имеют встроенный регуляризатор и могут сами игнорировать неинформативные входы в процессе обучения.

На этом мы завершим раздел экспериментов по ОИП на стандартных методах. И в следующем разделе я обосную и покажу практическое применение, на мой взгляд, статистически достоверного и делающего свою работу неплохо, метода на основе информационных метрик.

Источник.

Нужно начать с понятия информационной энтропии. Энтропия (шенноновская) — это синоним неопределенности. Чем более мы неуверенны относительно значения случайной величины, тем больше энтропии (еще один синоним — информации) несет реализация данной велич

© Habrahabr.ru