Метод генерации столбцов для решения задач математической оптимизации большой размерности07.05.2023 13:01

Недавно на хабре мне понравилась статья «Математическая оптимизация и моделирование в PuLP: задача о назначениях» , где автор и, как я потом узнал, мой знакомый решил сделать серию статей о математической оптимизации, с целью популяризовать это направление и максимально доступно ознакомить читателей с инструментами, позволяющими решать такой класс задач, и научить пользователя видеть такие задачи в реальном мире, чтобы понимать, где может оказаться полезен этот инструмент. Так, в своей статье автор описывает решение задачи назначения ресурсов на потенциальные работы с помощью верхнеуровневой питоновской оболочки pulp с подключением солвера cbc для решения самой задачи смешанного целочисленного программирования.

Мне очень понравился его идея, ведь такой набор статей может расширить кругозор людей из разных областей — ученых по данным, бизнес-аналитиков, архитекторов и всех-всех-всех. Как итог, она меня мотивировала написать серию статей о методах решения задач с большой размерностью с помощью специфических алгоритмов целочисленной оптимизации. Если статьи будут интересны читателю, то для удобства восприятия я также буду использовать питоновскую библиотеку pulp для моделирования.

Теперь к истокам задачи: часто, чтобы математическая модель была применима в реальном секторе, необходимо использовать очень много ограничений и большое количество переменных. Задачи, возникающие в бизнесе в реальных условиях, требуют использования моделей с большим количеством ограничений и большим количеством переменных.  Временами задача в лоб может и не решиться, поэтому были придуманы различные трюки. Один из них — метод «генерации столбцов» (Column generation).

Материал с деталями работы алгоритма кажется весьма объемным, и, чтобы не перенасыщать текущую статью, я решил разбить ее на три части, которые, по сути, можно читать независимо, но при прочтении всех трех у читателя сложится представление, как работает сам алгоритм. В первой части я рассмотрю постановку задачи раскроя и два алгоритма решения (в лоб и с помощью паттернов или шаблонов разрезов), во второй статье будет приведено описание самого алгоритма динамической генерации столбцов, а в третьей — рассмотрено решение задачи о назначениях, чтобы у читателя сложилось понимание о широких возможностях применения метода. Теоретическое описание метода было взято из следующего источника.

(Естественно, если первая статья в серии не понравится, то я приму свое авторское решение — далее не публиковать, чтобы не увеличивать количества нудной и ненужной информации в сети.)

Постановка задачи: Есть фирма, она закупает с завода металлические рулоны определенной ширины, например 10 дюймов.  Со стороны покупателей приходят заказы на продукцию разной ширины. Например, приходят заказы на рулоны с меньшейшириной. Так одной фирме нужна обрезка этих рулонов шириной 3 дюйма, другой фирме нужны обрезки в 5 дюймов, третьей — 6, четвертой — 9. Цель фирмы — нарезка исходных рулонов таким образом, чтобы выполнить все заказы и использовать наименьшее количество исходных рулонов. Данные о количестве заказанной продукции представлены в таблице ниже.

Количество заказов bi

Ширина заказанного рулона wi, дюймы

9

3

79

5

90

6

27

9

Исходные данные для решения задачи определяются в классе Data: 

@dataclass
class Data:
    '''Исходные данные для модели.'''
    # Максимальная ширина исходных рулонов.
    RAWS_WIDTH = 10
    # Количество заказов в штуках каждого типа рулонов.
    orders = [9, 79, 90, 27]
    # Ширина заказов каждого типа. Соответствие по индексу в списке.
    # Так необходимо 9 рулонов ширины 3, 79 рулонов ширины 5 и т.д.
    order_sizes = [3, 5, 6, 9]
    # Список паттернов, по каким может быть нарезан исходный рулон.
    # Так, например, паттерн [1, 0, 1, 0] означает, что из исходного рулона ширины 10,
    # может быть вырезан рулон ширины 3 и рулон ширины 6.
    patterns = [[0, 0, 0, 1],
                [0, 0, 1, 0],
                [1, 0, 1, 0],
                  [0, 1, 0, 0],
                [0, 2, 0, 0],
                [1, 1, 0, 0],
                [1, 0, 0, 0],
                [2, 0, 0, 0],
                [3, 0, 0, 0]]
    # Общее количество заказов.
    RAWS_NUMBER = sum(orders)

Напомню, что для постановки задачи смешанного целочисленного программирования требуется задать:

·       переменные модели — те значения, которые нам необходимо перебрать и выбрать, при каких их значениях целевой показатель достигает оптимума, в нашем случае — это какой исходный рулон разрезать и какие типы заказов оттуда вырезать.

·       ограничения, характеризующие физические, технические, законодательные условия, которые должны быть выполнены, в рассматриваемой задаче, например, условие, что мы должны выполнить абсолютно все заказы.

·    целевую функцию, которую мы хотим оптимизировать, в нашем случае это
минимизация количества разрезанных рулонов.

Решение 1. Модель Канторовича. Решение в лоб.

Импортируем необходимые библиотеки, инициализируем модель и перепишем бизнес постановку задачи в сначала в математическом виде, потом в программном.

import pulp
import numpy as np
import itertools as it
from dataclasses import dataclass
from collections import Counter
#  Инициализация модели.
model = pulp.LpProblem('Kantorovich model', pulp.LpMinimize)

·  1. Переменные

Предположим, что у нас есть всего K рулонов исходной длины. В этом случае для каждого рулона будет заведена переменная:

y_{k}=\left \{ \begin{array}{ccc} &1&, если \ исходный \ рулон\ выбран\ для\ разреза; \\ &0&, если \ исходный \ рулон\ остается\ не\ тронут.\\ \end{array} \right .

Чтобы выполнить все заказы, нам точно хватит K = 9 + 79 + 90 +27 = 215 исходных рулонов, если из одного исходного заказа мы будем вырезать один рулон одного типа. Естественно, это не оптимально, так как с одного рулона можно вырезать несколько заказов различных типов. Тем не менее заведем все 215 переменных, пусть и в результате решения большая их часть окажется нулями. Добавим эти переменные: 

# Задание типа переменных (возможность указать их не только целочисленными неоходима 
# для оценки целевой функции линейной релаксации).
#vars_type = pulp.LpContinuous
vars_type = pulp.LpInteger

# Создание необходимых индексов для переменных, для каждого исходного рулона.
cuts_ids = range(data.RAWS_NUMBER)
# Создание переменных, соответствующих y_{k}.
cuts = pulp.LpVariable.dicts("raw_cut", cuts_ids, lowBound=0, upBound=1, cat=vars_type)

За x_{ik}обозначим переменную, которая будет равна, количеству производных рулонов типа i \in Iвырезанного из исходного рулона k, где Iнабор всех типов рулонов, которые требуются покупателям. Добавим эти переменные в модель: 

# Создание необходимых индексов для переменных, для каждого исходного рулона.
cuts_ids = range(data.RAWS_NUMBER)
order_types_ids = range(len(data.orders))
items_ids = list(it.product(order_types_ids, cuts_ids))

# Создание переменных, соответствующих x_{i,k}.
items = pulp.LpVariable.dicts("item", items_ids, lowBound=0, cat=vars_type)

2. Ограничения

Сумма всех переменных x должна быть больше, чем размер заказа определенного типа, то есть мы должны выполнить все заказы всех типов:

\sum_{k=1}^{K}x_{ik} \geq b_i, \forall i \in I

Добавление этого ограничения в модель, может быть реализовано в следующем виде: 

# Любой заказ должен быть выполнен.
for t in order_types_ids:
    model += pulp.LpConstraint(pulp.lpSum(items[t, c] for c in cuts_ids) >= data.orders[t],
                               name="min_demand_{}".format(t), sense=pulp.LpConstraintGE)

Кроме того, есть правило, что из одного рулона мы не можем произвести больше заказов, чем его длина. Это правило кажется очевидным, но в модель оно тоже должно быть добавлено:

\sum_{i=1}^{m}x_{ik}w_{i} \leq y_{k}W, \forall k \in K

# Рулон не может быть разрезан на составляющие большие по ширине, чем тот рулон, из которого его вырезали.
for c in cuts_ids:
      model += pulp.LpConstraint(pulp.lpSum(data.order_sizes[t] * items[t, c]
                                            for t in order_types_ids) <= data.RAWS_WIDTH * cuts[c],
                                 name="max_width_{}".format(c), sense=pulp.LpConstraintLE)

Так, например, если не был выбран рулон к разрезу y_k=0, то это автоматически означает, что все соответствующие x_{ik}тоже должны быть равны нулю, так как выполняется неравенства x_{1k}w_1+...+x_{mk}w_k \leq y_k W =0, а x_{ik}и w_{k}— положительные.

· 3. Целевая функция

Таким образом, нашей цель — минимизировать количество использованных исходных рулонов:

z=\sum_{k=1}^{K}y_{k} \rightarrow min

# Добавляем в модель целевую функцию.
model += pulp.lpSum([cuts[c] for c in cuts_ids])

Решаем сформулированную задачу и выводим полученный результат: 

model.solve()

used_patterns = []
for c in cuts_ids:
    if cuts[c] >= 0.001:
        used_patterns.append(tuple([items[t, c].varValue for t in order_types_ids]))
print("Значение целевой функции {}:".format(model.objective.value()))
print("Каким образом нарезались искодные рулоны {}".format(dict(Counter(used_patterns))))

В текущем случае, целевая функция целочисленной задачи равна 157, то есть для выполнения всех заказов, нам понадобится столько штук исходных рулонов. При этом задачу можно решить быстро, — убрать требование на целочисленность переменной и воспользоваться, например, симплекс методом. Решение релаксированной (без требования того, чтобы переменные были целыми) задачи равно 120,5, что находится очень далеко от нужного нам целочисленного решения. При этом, при других типах заказов, эта разница может и дальше существенно расти. Таким образом, если задача будет большой, то пользуясь текущим методом, мы в принципе ее не сможем решить или получим очень плохое решение.

Полный код модели можно найти здесь.

Решение 2. Модель Гилмора-Гомори. Решение с помощью паттернов разреза (столбцов).

Трюк этого подхода заключается в том, что в случае, когда мы можем заранее перечислить все паттерны по которым может быть нарезан исходный рулон, то можно значительно сократить количество переменных. Матрица (a_1, a_2, ..., a_n), где каждый ее столбец характеризует один паттерн содержит информацию о всех возможных шаблона разреза (один вариант разреза рулона — один столбец этой матрицы). Так например, если у нас заказ длины (3, 5, 6, 9), а ширина исходного рулона 10, то его можно разрезать на два куска, один ширины 3, а другой ширины 6. А соответствующий паттерн разбиения будет (1, 0, 1, 0). Так как мы взяли первый и третий элементы из списка с типами заказов. Паттерны разбиения, в нашем учебном примере представлены на рисунке ниже:

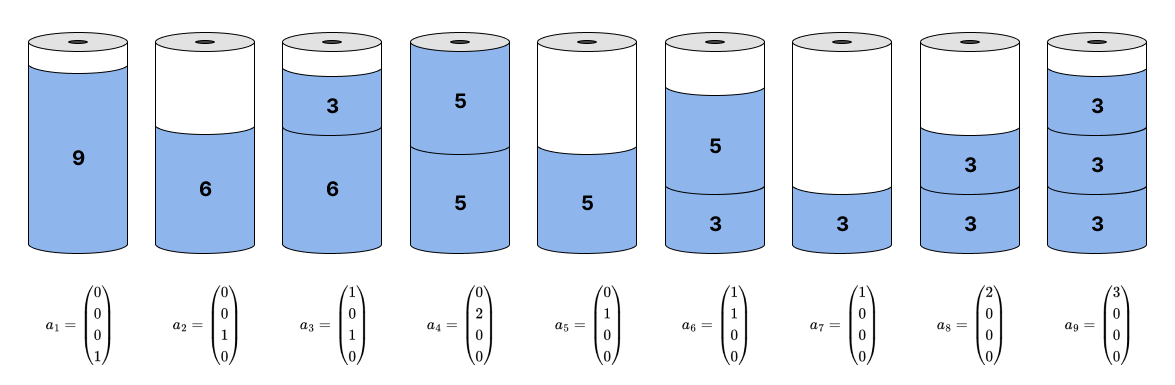
eb44a4cd0ac9f4e140cf919e8d29e762.png

Используя наличие паттернов, мы можем представить нашу модель в более простом виде:  

  1. Переменные x_j— количество паттернов (шаблонов разреза) j, которое нужно выбрать из всего возможного J множества паттернов.

  2. Ограничения.

    Сумма всех выполненных разрезов по паттернам должна быть больше, чем размер заказа определенного типа, то есть мы должны выполнить все заказы всех типов:

\sum_{j \in J}a_{ij}x_{j} \geq b_{i}, \forall i \in I

  1. Целевая функция

    Цель — минимизация количества используемых паттернов, то есть минимизация количества использованных исходных рулонов.

z_p= \sum_{j \in J}x_j \rightarrow min

Основным отличием от предыдущего подхода, — сейчас мы ищем необходимое количество заранее известных паттернов. Как следствие, у нас в модели используется существенно меньшее количество переменных.

Код модели: 

model = pulp.LpProblem('Gilmore-Gomory model', pulp.LpMinimize)

# Создание необходимых индексов для переменных.
patterns_ids = range(len(data.patterns))
order_types = range(len(data.orders))

# Создание переменных модели.
pattern_vars = pulp.LpVariable.dicts('patterns', patterns_ids, lowBound=0, cat=vars_type)

# Создание ограничения по обязательности выполнения всех заказов
for t in order_types:
    model += pulp.LpConstraint(
        pulp.lpSum(np.multiply(pattern_vars[p], data.patterns[p])[t]
                    for p in patterns_ids) >= data.orders[t],
        sense=pulp.LpConstraintGE, name="min_demand_{}".format(t))

# Добавление целевой функции в модель, необходимой для минимизации количества используемых паттернов.
model += (pulp.lpSum(pattern_vars[p] for p in patterns_ids))
model.solve()
    
used_patterns = {}
for p in patterns_ids:
    if pattern_vars[p].varValue >= 0.001:
        used_patterns[tuple(data.patterns[p])] = pattern_vars[p].varValue

print("Значение целевой функции {}:".format(model.objective.value()))
print("Каким образом нарезались искодные рулоны {}".format(dict(Counter(used_patterns))))

Теперь релаксация задачи нам дает следующее решение: x_1 =27, то есть мы должны из 27 исходных рулонов вырезать 27 рулонов по 9 дюймов, x_2=27, то есть, из 27 исходных рулонов, мы должны вырезать рулоны шириной 6 дюймов, x_3 = 9, из 9 исходных рулонов вырезать из каждого рулоны 3 и 6 дюймов, x_5= 39.5 и из 39.5 рулонов вырезать по два рулона по 5 дюймов. Видно, что целевое значения функции в этой постановке равно 156.5, и значительно ближе к целочисленному решению, которое равно 157. И округляя x_5до ближайшего целого мы точно получаем точное решение целочисленной задачи.

Естественно, количество паттернов (шаблонов) в реальных задачах значительно больше, чем в текущей, иллюстративной и может достигать десятков и сотен миллионов. Кроме того не ясно, как создавать эти паттерны, если их нет в исходных данных. Тем не менее, можно развить существующих алгоритм и стартовать всего лишь с несколько известных паттернов, а потом к ним уже добавлять, только те шаблоны, которые будут улучшать решение. Как это реализуется, — является материалом следующей статьи.

© Habrahabr.ru