Матрица-Перематрица15.05.2021 22:49

Тензор превращается в матрицу

Работа нейронной сети основана на манипуляциях с матрицами. Для обучения используются разнообразные методы, многие из которых выросли из метода градиентного спуска, где необходимо умение обращаться с матрицами, вычислять градиенты (производные по матрицам). Если заглянуть «под капот» нейронной сети, можно увидеть цепочки из матриц, выглядящие зачастую устрашающе. Проще говоря, «нас всех подстерегает матрица». Пора познакомиться поближе.

Для этого сделаем следующие шаги:

рассмотрим манипуляции с матрицами : транспонирование, умножение, градиент;
построим игрушечную нейронную сеть;
познакомимся с методом обратного распространения ошибки с использованием метода градиентного спуска.

Все шаги сопровождаются примерами кода с использованием только NumPy . Вычисления, не выходящие, впрочем, за рамки элементарной математики, приведены подробно. За индексами придется внимательно следить, но не отчаивайтесь, просто представьте, что каждый индекс — винтик, который надо закрутить, следуя простым правилам, но не пропустить. Если вдруг не разберетесь, ничего страшного — одно из двух: либо сбой в матрице, либо одно из двух.

Матрицы — они же тензоры

Основная структура данных в системах машинного обучения — тензор, который, по сути, является многомерным массивом. Тем не менее, тензор звучит солиднее, причем настолько, что он вошел в название библиотеки машинного обучения Google TensorFlow.

Итак, определим одномерный массив, он же тензор с единственной осью, он же тензор первого ранга, или просто вектор, который будем обозначать $a_{i}$ , где индекс i = 0, 1, 2, …, n-1 ; — размерность вектора.

import numpy as np # импорт модуля numpy
a=np.array([1,2,5])
a.ndim # одномерный тензор, количество осей = 1
a.shape # длина массива по каждой оси (3,)
a.shape[0] # длина массива по нулевой оси = 3

Скалярное произведение двух векторов $a_{i}\cdot b_{i}= a_{0}\cdot b_{0}+a_{1}\cdot b_{1}+a_{2}\cdot b_{2}$ . Отметим, что по повторяющимся индексам производится суммирование, здесь пробегает значения от 0 до 2 включительно.

b=np.array([3,4,7])
np.dot(a,b) # скалярное произведение = 46
a*b # поэлементное произведение array([ 3,  8, 35])
np.sum(a*b) # = 46

Теперь перейдем к двумерному тензору (тензору второго ранга) — матрице, элементы которой выводятся как $A_{i, j}$ . Например, $A_{0, 2}$ — элемент матрицы на пересечении 0-й строки и 2-го столбца. Из определения ясно, что матрица имеет две оси.

A=np.array([[ 1,  2,  3],
            [ 2,  4,  6]])
A # array([[1, 2, 3],
  #        [2, 4, 6]])
A[0, 2] # элемент на нулевой строке, во втором столбце = 3
A.shape # (2, 3) матрица имеет 2 строки, 3 столбца

При умножении матрици получаем матрицу C=AB , элементы которой $C_{i,k}=A_{i, j}B_{j, k}$ . Поскольку по повторяющимся индексам производится суммирования, количество столбцов матрицыдолжно совпадать с количеством строк (первое измерение совпадает с нулевым измерением)

B=np.array([[7, 8, 1, 3],
            [5, 4, 2, 7],
            [3, 6, 9, 4]])
A.shape[1] == B.shape[0] # true
A.shape[1], B.shape[0] # (3, 3) 
A.shape, B.shape # ((2, 3), (3, 4))
C = np.dot(A, B)
C # array([[26, 34, 32, 29],
  #        [52, 68, 64, 58]]); 
  #  например, C[0,1]=A[0,0]B[0,1]+ A[0,1]B[1,1]+A[0,2]B[2,1]=1*8+2*4+3*6=34
C.shape # (2, 4)

Если попытаемся умножить , то:

np.dot(B, A) # ValueError: shapes (3,4) and (2,3) not aligned: 4 (dim 1) != 2 (dim 0)

Первая размерность матрицы не совпадает с нулевой , о чем красноречиво и говорится.

Посмотрим, как построить матрицу из двух векторов. Для этого из векторов сделаем матрицы с одним столбцом, элементы которой $a_{i, 0}$ и $b_{j, 0}$ . Затем имеем $D_{i,j}=a_{i,0}b_{j,0}$ . Повторяющийся индекс есть, но он стоит не внутри произведения, как прописано в правилах для произведения матриц, поэтому воспользуемся тождеством $b_{j, 0}=(b.T)_{0, j}$ , где b.T — транспонированная матрица (используем обозначения NumPy). В результате имеем $D=a\cdot b.T$ . Любопытно, что операция транспонирования приводит $D.T=(a\cdot b.T).T=(b.T.T)\cdot a.T=b\cdot a.T$ .

a = np.reshape(a, (3,1)) # изменяет форму тензора, от a.shape = (3,) к (3,1),
b = np.reshape(b, (3,1)) # три строки, один столбец
D = np.dot(a,b.T)
D # array([[ 3,  4,  7],
  #        [ 6,  8, 14],
  #        [15, 20, 35]])

Игрушечная нейронная сеть

Вводим матрицу на входе, получаем результат на выходе. Поскольку мы тренируемся на подготовленном наборе данных, на выходе знаем нужный ответ.

Представим себе нейронную сеть как черный ящик с ручками, которыми можно манипулировать так, чтобы значения на выходе из нашего ящика как можно меньше отличались от тестового результата. Мера отклонения выводится с помощью функции потерь (cost function). Отметим, что в одну сторону ручки крутятся полегче. Туда осторожно и крутим. Когда все данные из тренировочного набора прошли один раз, и каждую ручку покрутили с выбранным шагом (learning rate), говорят, произошла одна эпоха (epoch). И так повторяем до тех пор, пока уменьшается функция потерь. Далее записываем показания ручек (веса), которые вместе с архитектурой и методом коррекции весов представляют собой исчерпывающий набор данных относительно обученной нейронной сети. Теперь мы можем засунуть в наш черный ящик любые разумные данные и получить наиболее вероятный ответ. Раньше этим занимались разумные животные, теперь ситуация изменилась, но как не было разумного подхода, так до сих пор и нет.

Время первых

Разберем простую нейронную сеть, показанную на рисунке из статьи (рекомендую посмотреть, есть русский перевод).

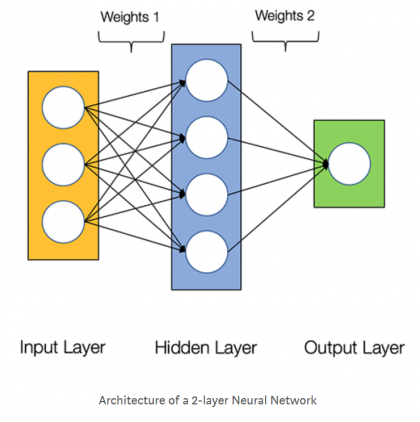
На входе имеем подготовленные данные — совокупность образцов (samples) . Каждый образец представлен вектором с тремя компонентами. Таким образом, все данные представлены тензором второго ранга (матрицей), первая ось которого (ось с нулевым индексом) — ось образцов (samples), вторая — ось признаков (features).

Для обучения нейронной сети имеем подготовленный тренировочный набор, в котором каждый образец имеет определённый выход (целевые данные). Это может быть распределение по классам (мужчина, женщина и …) или, например, значение температуры кончика носа для заданных параметров. Нам необходимо построить такую модель, чтобы значения на выходе как можно меньше отличались от значений из тренировочного набора.

Полный вперед!

Давайте пройдемся по нашей нейронной сети от начала до конца, посмотрим, что где лежит. Мы не будем ничего запоминать, просто погуляем по »Дворцу памяти» . Там не так много места, поскольку это всего лишь произведения матриц, которые разворачиваются от начала до конца. Мы вольны делать с ними все что угодно, только надо контролировать, чтобы каждая последующая матрица правильно зацеплялась с предыдущей по правилу умножения матриц. Есть матрицы с данными, и есть матрицы с параметрами, которые впоследствии подстроим, когда пойдем в обратный путь.

Вход

Предположим, на входе имеем 10 экземпляров векторов с трем признаками. Таким образом, матрица на входе имеет форму (10, 3). Пока возьмем ее «с потолка», заполним случайными числами. Существует несколько вариантов, как это можно сделать. Итак, можно заполнить матрицу:

целыми в диапазоне, например, от 0 до 50;

X=np.random.randint(0, 50, (10, 3))

равномерно распределенными в диапазоне от 0 до 1;

X=np.random.rand(10, 3)

распределёнными по нормальному закону со средним $\mu=2$ и дисперсией $\sigma ^2=16$ . Нормальное распределение, или распределение Гаусса, обычно обозначается как $N(\mu,\sigma^2)$ ;

X=4*np.random.randn(10, 3) + 2

Когда $\mu=0$ и $\sigma = 1$ , имеем дело со стандартным нормальным распределением.

Выход

Итак, на входе имеем матрицу с формой (10, 3) Теперь нам надо определить матрицу весов $W^{(1)}$ , чтобы подать значения на внутренний слой с четырьмя нейронами. Если значения в тренировочном наборе полностью определены при постановке задачи обучения, первоначальные значения весов задаются действительно произвольно, полагаясь впоследствии на методы их корректировки. Очевидно, что, вспоминая правила умножения матриц, $W^{(1)}$ должна иметь форму (3, 4) . Полезно себе представить, что $(10, 3)(3, 4)\Rightarrow(10, 4)$ . В результате, на внутренний слой приходит матрица $X\cdot W^{(1)}$ с формой (10,4) , на которую действует — причем весьма необычным способом — функция активации , выбранная должным образом для внутреннего слоя. Функция действует на каждый элемент матрицы независимо от другого элемента. Иными словами, если есть матрица с формой (m,n) (строк, столбцов) и с элементами $a_{i,j}$ , то после действия функции f(A) получим матрицу с той же формой, элементы которой равны $f(a_{i,j})$ ; просто, например, имеем $a_{1,2}\Rightarrow f(a_{1,2})$ , и так для каждого элемента. На выходе для каждого образца получим число, поэтому проблема выбора матрицы весов $W^{(2)}$ становится тривиальной, поскольку она должна иметь форму (4, 1) . Таким образом, $(10, 3)(3, 4)(4, 1)\Rightarrow(10, 1)$ . Итак, наше предсказание $\hat{Y}$ представлено в виде матрицы с 10-ю строчками (samples) и одним столбцом. В матричном виде все выглядит тривиально:

$\hat{Y}=X\cdot W^{(1)}\cdot W^{(2)}, \quad\quad \hat{Y}_{i,0}=X_{i,j} W_{j,k}^{(1)} W_{k,0}^{(2)}.$

Напоминаем, что нумерация начинается с нуля. Для наглядности мы пока не включили функции активации и смещения (bias).

Проверим на коде. Задача состоит в следующем: создать имитацию данных на входе, построить матрицы весов, получить значение на выходе, следить за формой.

X=np.random.randint(0, 50, (10, 3))
w1=2*np.random.rand(3,4)-1 # матрица случайных чисел в диапазоне от -1 до +1
w2=2*np.random.rand(4,1)-1
Y=np.dot(np.dot(x,w1),w2) # значения на выходе
Y.shape # (10, 1)
Y.T.shape # (1, 10)
(np.dot(Y.T,Y)).shape # (1, 1), смотрим, что получается при свертке

На выходе получили числа внутри матрицы с формой . Мы специально выбирали веса в диапазоне от -1 до +1, исходя из собственных «мутных» соображений (пока это не принципиально).

Теперь включим функции активации. Первая функция f_1 будет действовать на вход «скрытого слоя», вторая — на выход. В результате имеем

$\hat{Y}_{i,0}=f_2(f_1(X_{i,j} W_{j,k}^{(1)})W_{k,0}^{(2)}),$ $\hat{Y}=f_2(f_1(X \cdot W^{(1)})\cdot W^{(2)}).$

Подавая значения на вход нейронной сети из тренировочного набора, мы должны сравнить наши предсказания с этими значениями. С этой целью определим функцию потерь

$\triangle=\sum_i(Y_{i,0}-\hat{Y}_{i,0})^2=\sum_i\widetilde{Y}_{i,0}^2=(\widetilde{Y}.T)_{0,i}\widetilde{Y}_{i,0}=(\widetilde{Y}.T)\cdot\widetilde{Y},$

где (X,Y) — тренировочный набор, и мы ввели обозначение $\widetilde{Y}_{i,0}=Y_{i,0}-\hat{Y}_{i,0}$ . Напомним, что для транспонированной матрицы справедливо соотношение $(\widetilde{Y}.T)_{0,i}=\widetilde{Y}_{i,0}$ .

Это все, что мы можем получить на выходе. Пора в обратный путь.

На самом деле никакого распространения нет. Выход нейронной сети — просто произведение матриц. Причем все должно быть построено таким образом, чтобы функция потерь оказалась минимальной. Для этого необходимо нужным образом подстроить параметры, входящие в матрицы весов.

Метод градиентного спуска

Функция потерь — это функция многих переменных, в роли которых выступают веса. Экстремальная точка функции f(x) находится из уравнения $f^{'}(x_0)=0$ , где «штрих » — производная. Если вторая производная в этой точке больше нуля, это будет минимум, и наоборот. Понятно, что решить уравнение со многими переменными затруднительно, поэтому и проверить экстремум не представляется возможным. Можно поступить проще: стартовать из произвольной точки в пространстве весов — она у нас уже задана, поскольку мы определили матрицу весов случайным образом, — затем двигаться в направлении минимума. Выберем одну переменную веса (напомним, их у нас уже 16 штук), при этом зависимость от этой переменной одномерная, если зафиксированы остальные. Двигаемся от нуля в положительном направлении. Если спускаемся вниз, $f^{'}(W)<0$ , мы должны продолжить движение, если поднимаемся по склону, $f^{'}(W)>0» src=«https://habrastorage.org/getpro/habr/upload_files/2b0/95c/777/2b095c777bd0ac0fa268b2d6dc1bdfb4.svg» /> , лучше вернуться назад в направлении к минимуму. Таким образом, изменение переменной должно быть пропорционально производной с отрицательным знаком. Для функции потерь имеем </p><img alt=$

или для компонент

$W_{i,j}\Rightarrow W_{i,j}+\mu\cdot\delta W_{i,j}=W_{i,j}-\mu\cdot\frac{\partial \triangle}{\partial W_{i,j}},$

где $\mu$ — коэффициент скорости обучения (learning rate). Как видно, в этой формуле стоят производные по матрицам. Производные в этих формулах еще называют градиентом . Для векторов — это нормально, а для тензоров, почему бы и нет. Тем более, название самого метода — градиентный спуск .

Производные по матрицам. Вычисление градиентов

Для вычисления производных по матрицам необходимо руководствоваться правилом

$\frac{\partial a_{m, n}}{\partial a_{i,j}}=\delta_{m,i}\delta_{n,j},$

где $\delta_{i,j}$ - символ Кронекера, который отличен от нуля только тогда, когда i=j . Например, $\delta_{1,1}=1$ , а уже $\delta_{2,1}=0$ . Но самое главное: внимательно отслеживать индексы и никуда не спешить.

Для производной от функции потерь по матрице имеем

$\frac{\partial \triangle}{\partial W_{m,n}}=-2\sum_i(Y_{i,0}-\hat{Y}_{i,0})\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,n}}=-2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,n}},$

где, напомним, $\widetilde{Y}_{i,0}=Y_{i,0}-\hat{Y}_{i,0}$ , по повторяющимся индексам производится суммирование.

Градиент без активации. Пока проделаем вычисления без функций активации. Затем, когда освоимся в мире элементарного дифференцирования матриц, включим механизмы активации.

Итак, вспоминая $\hat{Y}_{i,0}=X_{i,j} W_{j,k}^{(1)} W_{k,0}^{(2)}$ , получим

$\frac{\partial \triangle}{\partial W_{m,0}^{(2)}}=-2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,0}^{(2)}}=-2\widetilde{Y}_{i,0}X_{i,j} W_{j,k}^{(1)}\delta_{k,m}=-2\widetilde{Y}_{i,0}X_{i,j} W_{j,m}^{(1)}=-2\widetilde{Y}_{i,0}(X\cdot W^{(1)})_{i,m}$

Напомним, для произвольной матрицы справедливо $A_{i,m}=(A.T)_{m.i}$ . Таким образом, окончательно получим следующее выражение:

$\delta W_{m,0}^{(2)}=-\frac{\partial \triangle}{\partial W_{m,0}^{(2)}}=2((X\cdot W^{(1)}).T)_{m,i}\widetilde{Y}_{i,0},$

или

$\delta W^{(2)}=2((X\cdot W^{(1)}).T)\cdot \widetilde{Y}.$

Посмотрим, получится ли, используя наши доморощенные данные, правильная форма для $\delta W^{(2)}$ . Поскольку $X\cdot W^{(1)}$ имеет форму (10,3)(3,4)=(10,4) , после транспонирования — (4,10) . Форма $\widetilde{Y}$ совпадает с формой $\hat{Y}$ — (10,1) . Таким образом, форма $\delta W^{(2)}$ равна (4,10)(10,1)=(4,1) , как и должно быть.

deltaW2=2*np.dot(np.dot(X,w1).T,Y)
deltaW2.shape # (4,1)

Теперь займемся $W^{(1)}$ .

$\frac{\partial \triangle}{\partial W_{m,n}^{(1)}}=-2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,n}^{(1)}}=-2\widetilde{Y}_{i,0}X_{i,j} \delta_{j,m}\delta_{k,n}W_{k,0}^{(2)}=-2\widetilde{Y}_{i,0}X_{i,m} W_{n,0}^{(2)}=-2(X.T)_{m,i}\widetilde{Y}_{i,0}(W^{(2)}.T)_{0,n},$ $\delta W^{(1)}=2(X.T)\cdot \widetilde{Y}\cdot (W^{(2)}.T).$

Индексы, которые «торчат наружу», некоторыми называются «говорящие » — в данном случае это и . Пока мы работаем с компонентами, сомножители можно произвольно переставлять, поскольку это всего лишь числа. Это мы и сделали: поставили члены с «говорящими» индексами впереди и сзади (если необходимо транспонировали), затем проследили, чтобы индексы правильно цеплялись друг за другом в соответствии с правилом умножения матриц.

Для формы $\delta W^{(1)}$ имеем: (3,10)(10,1)(1,4)=(3,4) .

Градиент с активацией. Надеюсь, те, кто следит за индексами, разобрались с результатами предыдущего раздела, когда не было никаких функций активации. Пришло время их включить. Дифференцировать по матрицам надо аккуратно, поскольку теперь матрицы весов скрыты под функциями. Мы рекомендуем сделать замены переменных, чтобы на каждом этапе дифференцирования имели дело только с одной матрицей. Надеюсь, правила дифференцирования сложной функции знакомы читателю, но на всякий случай напомним: если z=f(y(x)) , то производная от по равна $z_x^{'}=f_y^{'}y_x^{'}$ .

Итак,

$\hat{Y}_{i,0}=f_2(f_1(X_{i,j} W_{j,k}^{(1)})W_{k,0}^{(2)})\quad\Rightarrow\quad \hat{Y}_{i,0}=f_2(C_{i,0}),$

где используем очевидную цепочку замен:

$C_{i,0}=B_{i,k}W_{k,0}^{(2)}, \quad\quad B_{i,k}=f_1(A_{i,k}), \quad\quad A_{i,k}=X_{i,j} W_{j,k}^{(1)}.$

Матрица весов W_2 находится не так глубоко внутри функций, поэтому первоначально найдем градиент по этой матрице. Последовательно разворачивая цепочку дифференцирования, имеем

$\delta W_{m,0}^{(2)}=2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,0}^{(2)}}=2\widetilde{Y}_{i,0}\frac{\partial f_2(C_{i,0})}{\partial C_{\mu,0}}\frac{\partial C_{\mu,0}}{\partial W_{m,0}^{(2)}}=2\widetilde{Y}_{i,0}f_2^{'}(C_{i,0})\delta_{i,\mu}B_{\mu,k}\delta_{k,m}=2\widetilde{Y}_{i,0}f_2^{'}(C_{i,0})B_{i,m}.$

Действительно,

$\frac{\partial f_2(C_{i,0})}{\partial C_{\mu,0}}=f_2^{'}(C_{i,0})\delta_{i,\mu}, \quad\quad \frac{\partial C_{\mu,0}}{\partial W_{m,0}^{(2)}}=B_{\mu,k}\frac{\partial W_{k,0}^{(2)}}{\partial W_{m,0}^{(2)}}=B_{\mu,k}\delta_{k,m}.$

Напомним, здесь функция от матрицы — матрица с той же формой. Для перемещения индекса в начало цепочки поступаем как обычно: $B_{i,m}=(B.T)_{m,i}$ , аналогично для функций $f_1(A_{i,m})=(f_1(A).T)_{m,i}$ . Таким образом, в результате получаем

$\delta W_{m,0}^{(2)}=2(B.T)_{m,i}\widetilde{Y}_{i,0}f_2^{'}(C_{i,0}) \Rightarrow \delta W^{(2)}=2(B.T)\cdot(\widetilde{Y}*f_2^{'}(C))$

Остановимся подробнее на операции поэлементного умножения »*» матриц. Если у нас есть две матрицы, и , с одинаковой формой, то в результате действия операции поэлементного умножения a*b мы получим матрицу с той же формой, каждый элемент которой равен произведению элементов; например, третий элемент второй строки равен $a_{1,2}b_{1,2}$ .

Проиллюстрируем на коде. Пусть f_1(x)=x^2 и f_2(x)=x^3 . Эти функции будут принимать матрицы, затем возводить в степень по правилу, что каждый элемент матрицы независимо возводится в степень. Для этого в NumPy есть соответствующие функции.

def f1(x): # первая функция
    return np.power(x,2)
def graf1(x): # производная
    return 2*x
def f2(x): # вторая функция
    return np.power(x,3)
def gradf2(x): # производная
    return 3*np.power(x,2)

A=np.dot(X,w1) # вход внутреннего слоя
B=f1(A)        # выход скрытого слоя
C=np.dot(B,w2) # вход слоя на выходе
Y=f2(С) # значения на выходе
deltaW2=2*np.dot(B.T, Y*gradf2(C))
deltaW2.shape # (4,1)

Вычисление градиента по $W^{(1)}$ развернется в более длинную цепочку, но при этом здесь отсутствуют концептуальные сложности. Просто надо аккуратно двигаться вперед — шаг за шагом.

$\delta W_{m,n}^{(1)}=2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,n}^{(1)}}=2\widetilde{Y}_{i,0}\frac{\partial f_2(C_{i,0})}{\partial C_{\mu,\nu}}\frac{\partial C_{\mu,\nu}}{\partial B_{l,s}}\frac{\partial B_{l,s}}{\partial W_{m,n}^{(1)}},$

где $C_{\mu,\nu}=B_{\mu,k}W_{k,\nu}^{(2)}$ . Раздельно вычисляем производные:

$\frac{\partial f_2(C_{i,0})}{\partial C_{\mu,\nu}}=f_2^{'}(C_{i,0})\delta_{i,\mu}\delta_{0,\nu},\quad\quad \frac{\partial C_{\mu,\nu}}{\partial B_{l,s}}=\delta_{\mu,l}\delta_{k,s}W_{k,\nu}^{(2)},\quad\quad$ $\frac{\partial B_{l,s}}{\partial W_{m,n}^{(1)}}=\frac{\partial B_{l,s}}{\partial A_{r,e}}\frac{\partial A_{r,e}}{\partial W_{m,n}^{(1)}}=f_1^{'}(A_{l,s})\delta_{l,r}\delta_{s,e}\delta_{j,m}\delta_{e,n}X_{r,j}=f_1^{'}(A_{l,s})\delta_{l,r}\delta_{s,n}X_{r,m}.$

Собирая все вместе, получим

$\delta W_{m,n}^{(1)}=2\widetilde{Y}_{i,0}f_2^{'}(C_{i,0})\delta_{i,\mu}\delta_{0,\nu}\delta_{\mu,l}\delta_{k,s}W_{k,\nu}^{(2)}f_1^{'}(A_{l,s})\delta_{s,n}\delta_{l,r}X_{r,m}=2\widetilde{Y}_{i,0}f_2^{'}(C_{i,0})W_{n,0}^{(2)}f_1^{'}(A_{i,n})X_{i,m},$

где мы использовали очевидные свертки индексов

$\delta_{i,\mu}\delta_{0,\nu}\delta_{\mu,l}\delta_{k,s}\delta_{s,n}\delta_{l,r}=\delta_{i,l}\delta_{i,r}\delta_{k,n}\delta_{s,n}.$

Действительно, $\delta_{0,\nu}W_{k,\nu}^{(2)}=W_{k,0}^{(2)}$ , индексы и мы не трогаем, поскольку они «говорящие», так что остается побеспокоиться относительно l,r,k,s .

Теперь располагаем «говорящие» индексы в нужных местах, что приводит к соотношению

$\delta W_{m,n}^{(1)}=2(X.T)_{m,i}\widetilde{Y}_{i,0}f_2^{'}(C_{i,0})(W^{(2)}.T)_{0,n}f_1^{'}(A_{i,n}),$ $\delta W^{(1)}=2(X.T)\cdot [[(\widetilde{Y}*f_2^{'}(C))\cdot(W^{(2)}.T)]*f_1^{'}(A)].$

Действительно, если ввести вспомогательную матрицу $D_{i,o}=\widetilde{Y}_{i,0}f_2^{'}(C_{i,0})\Rightarrow\widetilde{Y}*f_2^{'}(C)$ , то при умножении получаем матрицу $F_{i,n}=D_{i.o}(W^{(2)}.T)_{0,n}$ , и дальше поэлементное умножение $F_{i,n}f_1^{'}(A_{i,n})\Rightarrow F*f_1^{'}(A)$ .

Проверим в коде.

deltaW1=2*np.dot(X.T, np.dot(Y*gradf2(C),w2.T)*gradf1(A))
deltaW1.shape # (3,4)

Основным результатом является получение выражения для градиентов. Но это лишь игра с камешками на берегу озера.

Послесловие

«То, что было — нынче сплыло. Прошлое прости-прощай!» А что дальше? Если некоторые термины для вас не знакомы, поройтесь, почитайте, но особо вникать не надо. Хотите научиться шить, для этого не следует годами изучать инструкцию для швейной машинки. Просто надо сесть и попытаться что-нибудь сделать, используя навыки, которыми вы обладаете. Садитесь и шейте! Думаю, если интересуетесь нейронными сетями, уже есть какой-то багаж навыков. Во всяком случае, здесь не место бахвалиться своими знаниями инструкций, как это принято у продвинутых знатоков библиотек.

Итак, что я рекомендую сделать сейчас же. У James Loy — автора статьи , которая и инспирировала настоящие заметки, есть отличная книга, в которую полезно, при желании, заглянуть. К этой книге прилагаются коды. Откройте коды к первой главе, в одном из них увидите воплощение того, чем мы занимались в этих заметках, но только на своих данных. Попробуйте обучить нейронную сеть на собственных данных с другой логикой «вход-выход», используйте другие функции активации, постройте графики, научитесь выводить время выполнения. Когда надоест баловаться и захочется более лёгкой жизни, значит пришло время связать свою жизнь с TensorFlow и Keras. Для этого много чего есть, но лучше начать с первоисточника (есть перевод на русский).

Пишите коды, вникайте в формулы, читайте книги, задавайте себе вопросы.

Что касается инструментов, то это Jupyter Notebook (Anaconda рулит!), Colab…