Математика в космонавтике: ротационный детонационный двигатель

Отправка кого-то или чего-то за пределы нашей планеты и по сей день является крайне сложным и дорогостоящим удовольствием. В то время как космические путешественники из различных научно-фантастических произведений массовой культуры используют ретрансляторы («Mass Effect»), варп-двигатели («Стартрек») или даже звездные врата («Звездные врата»), в реальности же все куда прозаичнее. На данный момент нам не известны такие нереальные технологии, потому мы используем ракетное топливо. Естественно, для запуска одного шаттла или ракетоносителя топлива нужно крайне много. Решить эту проблему может новый вид двигателей — ротационный детонационный. Пока процесс его разработки далек от завершения, ученые из Вашингтонского университета решили создать математическую модель данного устройства, чтобы лучше понять принцип его работы. Это позволит инженерам проводить точные тесты прототипов и лучше понимать, какие именно улучшения необходимо внедрять. Итак, как выглядит ракетный двигатель глазами математика и что удалось узнать благодаря моделированию? Ответы на эти вопросы ждут нас в докладе исследовательской группы. Поехали.
Основа исследования
Вполне очевидно, что для вывода космического аппарата за пределы атмосферы Земли требуется огромное количество энергии. Количество этой энергии зависит от используемого топлива и от двигателя аппарата. Вариантов первого существует немало, однако они далеки от научно-фантастических эквивалентов по своей эффективности. Потому немало внимания уделяется разработке именно нового типа двигателей.
Классический ракетный двигатель работает за счет экзотермической химической реакции горючего и окислителя. Когда эти два компонента топлива вступают в реакцию, генерируется много тепловой энергии и газообразного рабочего тела, которое расширяется. Это приводит к тому, что его внутренняя энергия преобразуется в кинетическую энергию реактивной струи. По своей сути этот химический процесс дефлаграционный, т.е. процесс дозвукового горения.
Дефлаграцию можно заметить на детонацию, когда по веществу распространяется ударная волна, инициирующая химические реакции горения. Тип двигателя, реализующий такую модель, называется импульсный детонационный двигатель, однако он также пока еще в разработке.
В рассматриваемом исследовании речь идет о ротационном детонационном двигателе (RDE, т.е. rotating detonation engine) — устройстве, создающее тягу, в котором самоподдерживающиеся ударные волны, вызванные горением (детонации) распространяются азимутально в кольцевой камере сгорания.
Горючее и окислитель впрыскиваются в канал, обычно через небольшие отверстия или щели (кольцевые зазоры). Благодаря узкому кольцевому зазору градиенты плотности и давления, вызванные тепловыделением, самоусиливаются, в конечном итоге образуя ударные волны, достаточно сильные для самовоспламенения топлива.
Стабильная работа RDE, являющаяся объектом исследования, объединяет в себе баланс нескольких аспектов: горение, впрыск и смешивание, выпуск и выброс энергии. Если эти переменные не сбалансированы, то возникает дестабилизация работы двигателя, которая проявляется в виде перехода к другому количеству волн или в виде модуляции скорости волны.
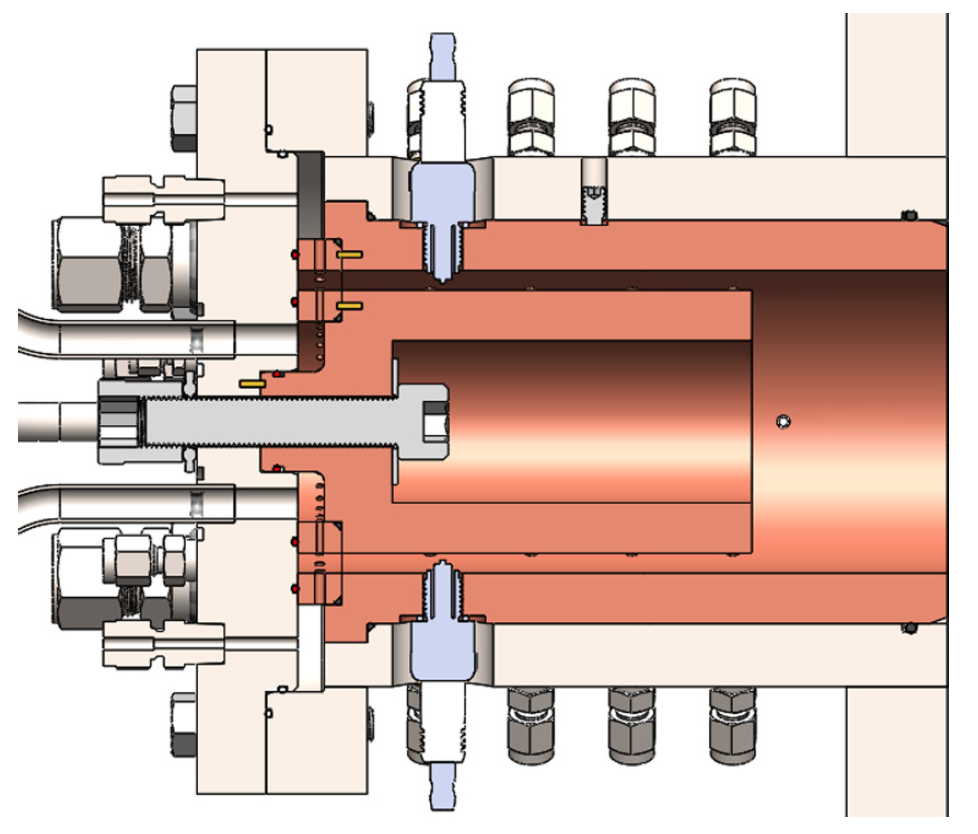
Изображение №1: схема RDE.
Вычислительное гидродинамическое моделирование RDE позволяет детально исследовать волновую структуру и потоковое поле* двигателя.
Потоковое поле* — распределение плотности и скорости жидкости в пространстве и времени.Векторное поле* — преобразования пространства, где каждая его точка отображается в виде вектора с началом в этой точке.
Однако, ранее подобная процедура была весьма затратной и сложной, как заявляют сами ученые. Кроме того, ранее созданные модели не могли вычленить факторы, влияющие на формирование бифуркации*.
Бифуркация* — качественное изменение поведения динамической системы при бесконечно малом изменении её параметров.
Несмотря на ожидаемые сложности, было решено проводить моделирование, но с использованием новых экспериментальных данных по нелинейной динамики вращающихся детонационных волн. Это позволило создать модель, которая учитывает самые незначительные изменения, тем самым фиксируя бифуркации, наблюдаемые на практике во время экспериментов.
Экспериментальная часть
Для проведения полноценно исследования и соответствующего моделирования были проведены определенные эксперименты. Для этого был специально подготовлен RDE и тестовая камера для изучения динамики вращающейся волны детонации. Двигатель, используемый для этого исследования, уникален тем, что его внутренние компоненты являются модульными. Части двигателя могут быть заменены для получения различных кольцевых зазоров и длины камеры сгорания. Также можно заменить инжектор, что позволяет исследовать разные варианты соединения и смешивания топлива.
Изображение №2
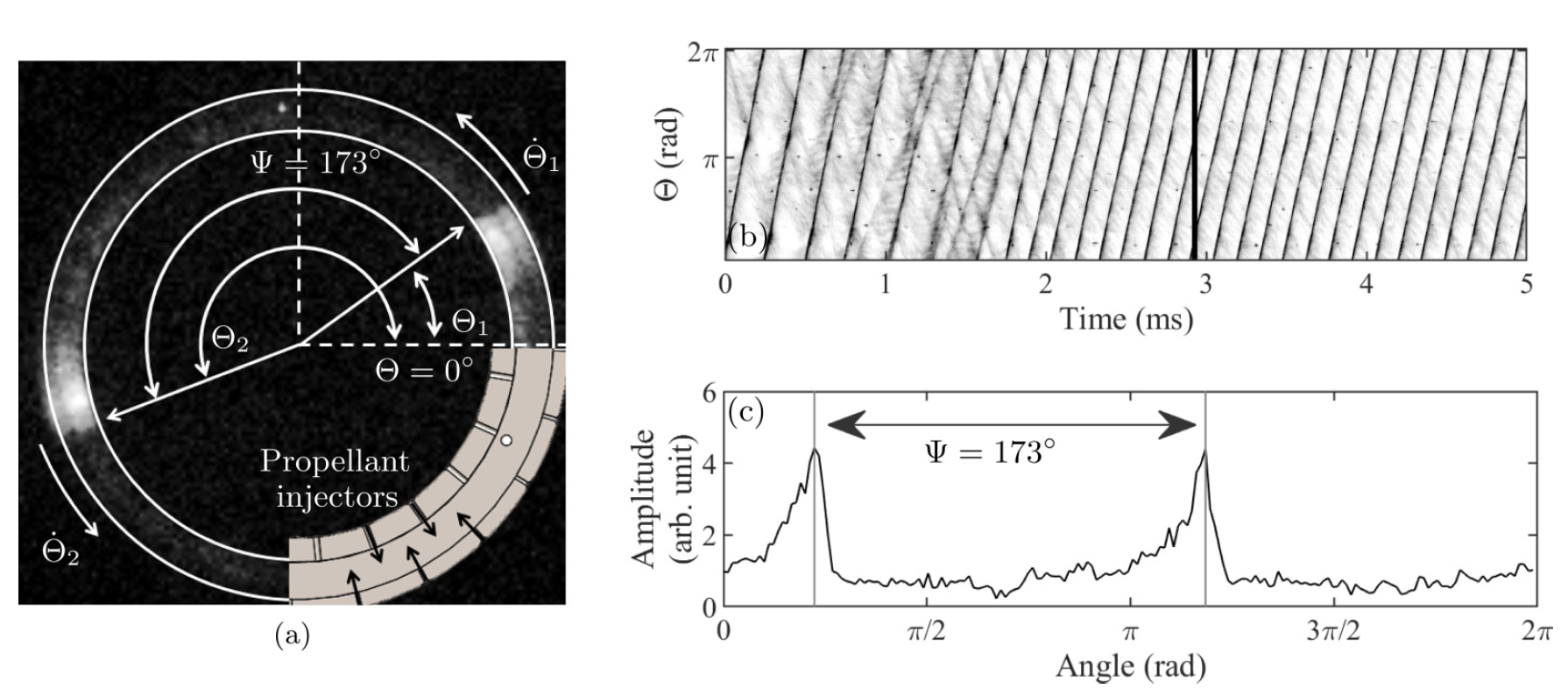
Тестовая камера оптически доступна, что позволяет регистрировать полную кинематическую историю всех детонационных волн с высоким пространственно-временным разрешением (2а).
Каждый эксперимент представляет собой 0.5 секундное сжигание газообразного метана и кислорода с заданной пропорцией и скоростью подачи. В успешном эксперименте искра зажигает смесь и производит ускоряющее пламя, которое переходит в ряд бегущих детонационных волн.
В основе данного исследования лежит предположение, что наблюдаемая светимость в экспериментах коррелирует с прогрессом сгорания. Следовательно, более яркие области демонстрируют более высокое тепловыделение, чем более темные области. Если это предположение правдиво, то можно рассмотреть несколько примеров форм сигналов, извлеченных из данных с высокоскоростной камеры.
Кинематика волны может быть получена из данных камеры с помощью алгоритма интеграции интенсивности пикселей и зафиксирована в виде диаграммы (2b).

Изображение №3
Записи камеры также могут быть преобразованы в волновую систему отчета, в этом случае разности фаз между волнами будет отчетливо видна.
На графике 3а представлены данные с 2b в виде волновой системе отчета, а на 3с показана соответствующая скорость отслеживаемой волны.
Для этих данных время было определено как τ = t (Dwave/L), где L — длина периодической области, а Dwave — скорость волны в состоянии синхронизации мод.
На 3а виден переход от одной волны к двум во время процесса запуска. При таком переходе мод после критической точки образуется вторая детонационная волна, которая начинает распространяться вокруг кольца. Однако расстояние между двумя волнами в кольцевом пространстве асимметрично, что вызывает дисбаланс в количестве топлива, потребляемого каждой из волн. Волна с координатой θ1, идущая за предыдущей волной θ2, существует с разностью фаз Ψ = θ2 — θ1 < π (). В этот момент, если предположить, что частота обновления топлива приблизительно постоянна, в хвостовой волне остается меньше половины доступного топлива в камере для его потребления. Поскольку тепловыделение ракетного топлива напрямую влияет на скорость детонации, задерживающая волна начинает замедляться. Однако предыдущая волна может обработать оставшуюся часть имеющегося топлива и ускориться за счет этого избытка. Таким образом, эти две волны ведут себя дисперсионно, когда они стремятся к устойчивому состоянию с максимальной и симметричной разностью фаз.
Для одноволновой части на 3а квазистационарная волна имеет скорость на 20–30% ниже скорости Чепмена-Жуге для ракетного топлива. Эта метрика является прямой наблюдаемой энергией, необходимой для поддержания детонационной волны, подверженной диссипации и восстановлению усиления в камере сгорания. Когда происходит переход к двум волнам и динамика устанавливается в устойчивое состояние, скорость волны уменьшается примерно до 90% от скорости одиночной волны.

Изображение №4
Если замедлить подачу топлива в конце эксперимента, то наблюдается противоположная ситуация. На 4а показан постепенный переход от 2 волн к 1 волне в течение примерно 10 мс. Две волны конкурируют за все более дефицитное топливо, в отличие от случая избыточного топлива, показанного на 3а.
Из-за начального возмущения разности фаз волны начинают регулярно обмениваться силой (скоростью и амплитудой), вызывая экспоненциальный рост неустойчивости. По мере возрастания колебаний разности фаз происходит катастрофическое взаимодействие между волнами, когда отстающая волна обгоняет впередиидущую во время одного из колебаний с большой амплитудой. После бифуркации скорость оставшейся волны примерно на 10% выше, чем у волны до неустойчивости.

Изображение №5
Также достаточно часто наблюдались волновые нестабильности, которые не приводили к изменению количества волн. На изображении №5 показана периодическая скорость волны и амплитуда, наблюдаемые в эксперименте с тремя вращающимися волнами. Это явная модуляционная нестабильность, поскольку спектральные боковые полосы сопровождают несущую частоту, соответствующую средней скорости бегущей волны в камере сгорания. Этот режим работы стабилен в том смысле, что он не приводит к раздвоению числа волн, если состояние потока существенно не нарушено.
В случае, если площадь инжектора была увеличена по отношению к площади кольцевой камеры, наблюдался импульсный режим работы, для которого характерен «вкл/выкл» режим работы инжекторов.

Изображение №6
На изображении выше продемонстрированы колебательные плоские волны при импульсном режиме работы.
Математическая модель
Для понимания того, какие именно физические аспекты доминируют в процессе формирования волн, в синхронизации мод и в бифуркаций мод была создана математическая модель, отражающая нюансы горения, впрыска топлива и диссипации энергии, структура которой определяется по следующим формулам:
∂η/∂t + η (∂η/∂x) = (1 — λ)ω (η) q0 + ϵξ (η)
∂λ/∂t = (1 — λ)ω (η) — β (η, ηp, s)λ
η (x, t) — свойства рабочего тела;
λ — переменная горения (λ = 0 — горенея не было, λ = 1 — полное сгорание);
ω (η) — функция тепловыделения;
q0 — тепловыделение и константа пропорциональности;
ϵξ (η) — функция потери энергии;
ϵ — константа потери;
β (η, ηp, s) — модель впрыска;
ηp и s — параметры впрыска.
Результаты экспериментов
Подготовив математическую модель, ученые провели ряд численных моделирований (т.е. симуляций) с указанными ниже параметрами:

На первом этапе моделирования было решено рассмотреть существование плоскостных решений для модельной системы, включая поведение предельного цикла*.
Предельный цикл* — один из возможных вариантов стационарного состояния системы. Предельный цикл векторного поля — замкнутая (периодическая) траектория векторного поля, в окрестности которой нет других периодических траекторий.
Задача Коши* была решена с применением начальных условий η (x, 0) = 1 и λ (x, 0) = 0.75.
Задача Коши* — поиск решения дифференциального уравнения, которое будет удовлетворять начальные условия (начальные данные).
Плоскостная волна колеблется около точки в фазовом пространстве, где горение истощение усиления и впрыск восстановление усиления совпадают [βλ = (1 — λ) ω (η)], при условии баланса входной энергии, отклонения энергии и диссипации энергии [ξ = (1 — λ))ω (η)q0].
Низкоэнергетические колебания затухают до плоского фронта дефлаграции без колебаний.
Пульсирующие фронты, подобные тем, которые наблюдались в ранее проведенных экспериментах, характеризуются периодической «активацией» и «дезактивацией» инжекторов, сначала резонирующих с выделением тепла, а затем насыщаемых механизмами потерь. Пример пульсирующего фронта плоской волны представлен на 6d.
Пульсирующие плосковолновые решения полной модели устойчивы для плоскостных начальных условий, но неустойчивы к возмущениям, поскольку они перерастают в бегущие детонационные волны
Начальными условиями Задача Коши для бегущей волны были: η (x, 0) = (3/2) sech2 (x — x0) и λ (x, 0) = 0 и λ (x, 0) = 0.
Была определена скорость Чепмена—Жуге (CJ) для данной системы (невязкой устойчивой волны, в которой вся энергия была передана в волну в бесконечно тонкой реакционной зоне). Эта постоянная скорость волны определяется как минимальная скорость, которая удовлетворяет условиям Ранкина-Гюгонио* для заданного тепловыделения. В отсутствие потерь эта минимальная скорость равна DCJ = (η1 + q0) + √ q0 (q0 + 2η1). В случае η1 = 0 скорость волны становится равной 2q0.
Адиабата Ранкина-Гюгонио* — математическое соотношение, связывающее термодинамические величины до и после ударной волны.
Эта скорость является метрикой, по которой измеряются бегущие волны в рассматриваемой модели.
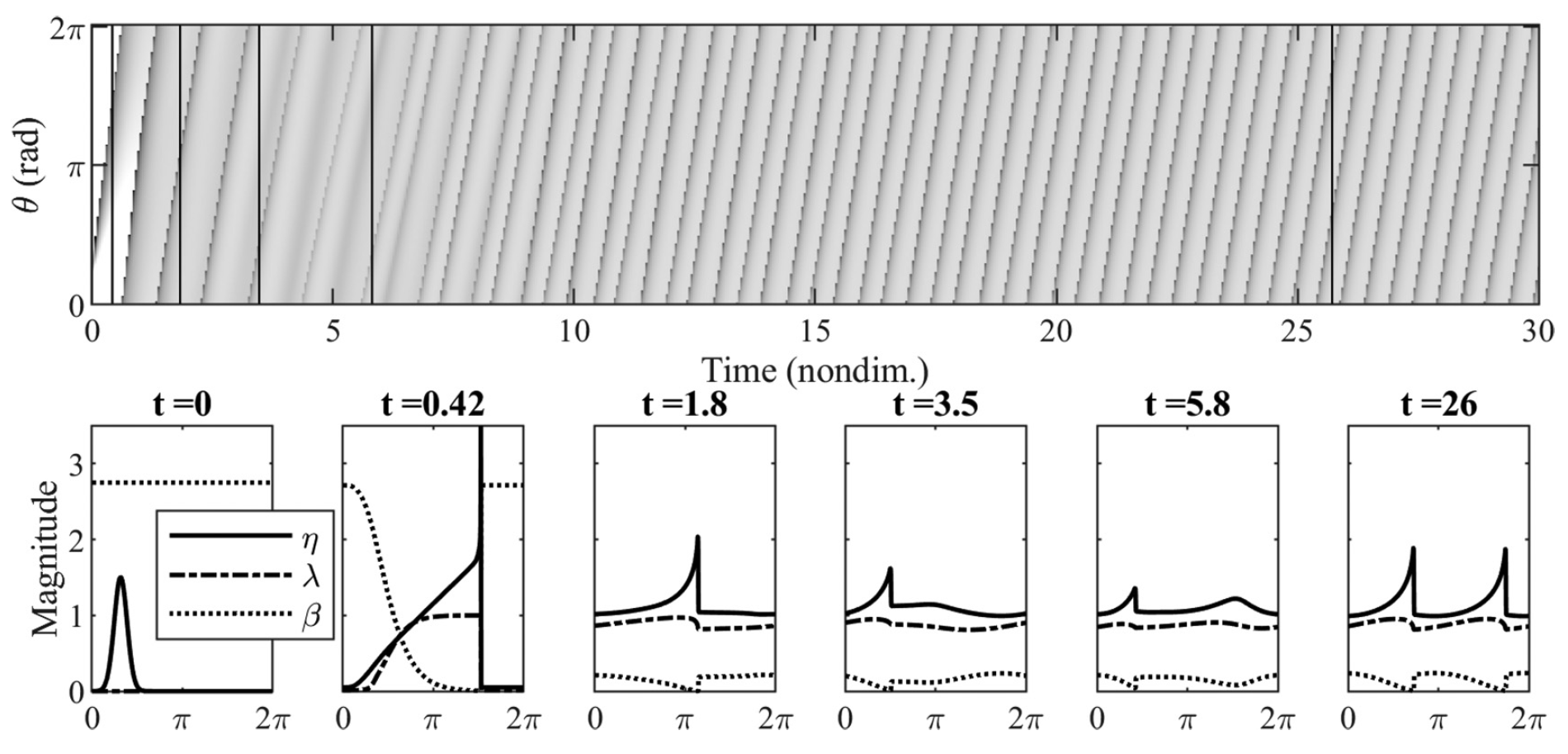
Изображение №8
На изображении выше представлена эволюция стандартного экспериментального моделирования. Поскольку начальный sech-импульс значительно выше ηc, среда локально и быстро выделяет тепло. Волна становится «острее» и образует детонацию. Этот начальный импульс распространяется со скоростью CJ, пока не достигнет своего хвоста, и в этот момент волна начинает быстро рассеиваться и замедляться: ограниченная величина горения не может продолжать поддерживать волну при DCJ = 2q0. Кроме того, быстрое тепловыделение (по сравнению со шкалой времени рассеяния энергии) исходной волны CJ приводит к увеличению среднего значения η в области, значительно превышающего значение η0 окружающей среды и значение ηc воспламенения.
Таким образом, эффективная энергия активации активной среды уменьшается, и во всей области повышается паразитная дефлаграция или медленное тепловыделение, не связанное с бегущими волнами. Поскольку время прохождения исходной бегущей волны было увеличено за счет рассеяния, паразитная дефлаграция имеет достаточно времени для завершения процесса дефлаграции-детонации (DDT, т.е. deflagration-to-detonation) и формирования множества детонационных волн с меньшей амплитудой.
Чтобы вызвать процесс перехода мод, когда имеется состояние стабильной моды, было использовано ступенчатое изменение s, что вызвало бифуркацию. Пример такого перехода показан на 4b, где две первоначально вращающиеся детонационные волны с синхронизацией мод становятся неустойчивыми и разрушительно раздваиваются.
Низкоамплитудные разности фаз возрастают экспоненциально, что наблюдалось и во время экспериментов (4а). В течение периода колебаний две волны обмениваются силой (амплитудой) и скоростью. Для заданной функции впрыска β и потерь скорость роста неустойчивости и период колебаний параметризуются степенью примененного шага в изменении параметров s и ηp.
При зарождении новой волны или разрушении существующей совокупность волн в тестовой камере действует дисперсионно, в конечном итоге формируя состояние с синхронизацией мод.

Изображение №9
Выше изображены бифуркационные диаграммы, показывающие зависимость количества волн, скорости волны и амплитуды волны от s и значения потерь. При увеличении s от нуля устойчивые плоские фронты дефлаграции образуются для небольших значений. Как только значение s может способствовать образованию бегущей волны, волны начинают демонстрировать лестницы, где их скорость постепенно увеличивается, пока не произойдет еще одна бифуркация. Эти волны возникают в результате паразитной дефлаграции в процессе DDT. При каждой бифуркации с увеличением числа волн скорость волны падает. Когда значение s становится достаточно большим, число волн увеличивается до тех пор, пока волновые фронты не станут малыми по амплитуде и не сольются в плоскостный фронт дефлаграции.
Для более подробного ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых.
Эпилог
Космические аппараты это невероятно сложные механизмы, объединяющие в себе знания множества научных направлений, физики, химии, математики, механики и т.д. На данный момент используемые ракетные двигатели используют целую вереницу механизмов управления и контроля реакции горения, чтобы она могла успешно обеспечить движения многотонной махины, пытающейся оторваться от земли. В случае ротационного двигателя большую часть обязанностей по этому вопросу берет на себя ударная волна. Это сильно сокращает объемы потребляемого топлива (учитывая, что примерная оценка эффективности детонации на ~25% выше, чем у классической дефлаграции), однако есть и ряд проблем. Основной является нестабильность таких волн. Как говорят сами ученые, любая детонация это неконтролируемый процесс, который протекает так, как ему вздумается.
Для того, чтобы понять этот хаотичный, на первый взгляд, процесс ученые создали математическую модель. Основой модели стали практические эксперименты с двигателем, продолжительность которых составила всего полсекунды, однако этого было достаточно для получения данных, необходимых для формирования модели.
Исследователи говорят, что их модель является первой в своем роде. Она дает возможность понять будет ли такой тип двигателей работать стабильно или же нет, а также оценить работу конкретного двигателя, использованного во время практической части опытов.
Другими словами, модель раскрывает карты того, какие физические процессы протекают во время работы системы. В дальнейшем ученые намерены усовершенствовать свое творение, чтобы его можно было применять уже для определения тех или иных аспектов, которые требуют особого внимания для реализации работающего и стабильного ротационного двигателя.
Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята. :)
Немного рекламы :)
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5–2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле в дата-центре Equinix Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5–2697v3 2.6GHz 14C 64GB DDR4 4×960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5–2430 2.2Ghz 6C 128GB DDR3 2×960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5–2650 v4 стоимостью 9000 евро за копейки?
