Математика в Gamedev по-простому. Кривые и дождь в Unity
Всем привет! Меня зовут Гриша, и я основатель CGDevs. Продолжим говорить про математику что ли. Пожалуй, основное применение математики в геймдеве и компьютерной графики в целом — это VFX. Вот и поговорим про один такой эффект — дождь, а точнее про его основную часть, требующую математики — рябь на поверхности. Последовательно напишем шейдер для ряби на поверхности, и разберём его математику. Если интересно — добро пожаловать под кат. Гитхаб проект прилагается.

Иногда наступает такой момент в жизни, когда программист должен взяться за бубен и призвать дождь. В целом сама по себе тема моделирования дождя очень глубокая. Существует множество математических работ по разным частям этого процесса от падения капли и эффектов связанных с этим до распределения капель в объёме. Разберём только один аспект — шейдер, который позволит нам создавать эффект похожий на волну от упавшей капли. Пора браться за бубен!
Математика волны
При поиске в интернете находишь очень много забавных математических выражений для генерации ряби. Часто они состоят каких-то «магических» чисел и периодической функции без обоснований. Но вообще математика подобного эффекта довольно простая.
Нам понадобится всего лишь уравнение плоской волны в одномерном случае. Почему плоской и одномерной разберём чуть позже.
Уравнение плоской волны в нашем случае может быть записано как:
Aresult = A * cos (2 * PI *(x / waveLength — t * frequency));
Где:
Aresult — амплитуда в точке x, в момент времени t
А — максимальная амплитуда
wavelength — длина волны
frequency — частота волны
PI — число ПИ = 3.14159 (float)
Шейдер
Your browser does not support HTML5 video.
Поиграемся с шейдерами. За «верх» будет отвечать координата -Z. Так удобнее в 2D случае в Unity. При желании шейдер будет не трудно переписать на Y.
Первое, что нам понадобится — это уравнение окружности. Волна нашего шейдера будет симметрична относительно центра. Уравнение окружности в 2д случае описывается, как:
r ^ 2 = x ^ 2 + y ^ 2
нам понадобится радиус, так что уравнение приобретёт форму:
r = sqrt (x ^ 2 + y ^2)
и это даст нам симметрию относительно точки (0, 0) в меше, что сведёт всё к одномерному случаю плоской волны.
Теперь напишем шейдер. Я не буду разбирать каждый шаг написания шейдера, так как это не цель статьи, но за основу берётся Standard Surface Shader из Unity, шаблон которого можно получить через Create→Shader→StandardSurfaceShader.
Кроме этого, добавляются проперти необходимые для волнового уравнения: _Frequency, _WaveLength и _WaveHeight. Проперти _Timer (можно было бы использовать время с гпу, но при разработке и последующем анимировании удобнее его контролировать вручную.
Напишем функцию getHeight получения высоты (сейчас это координата Z) подставив уравнение окружности в волновое уравнение
Написав шейдер с нашим волновым уравнением и уравнением окружности — получим такой эффект.
Shader "CGDevs/Rain/RainRipple"
{
Properties
{
_WaveHeight("Wave Height", float) = 1
_WaveLength("Wave Length", float) = 1
_Frequency("Frequency", float) = 1
_Timer("Timer", Range(0,1)) = 0
_Color ("Color", Color) = (1,1,1,1)
_MainTex ("Albedo (RGB)", 2D) = "white" {}
_Glossiness ("Smoothness", Range(0,1)) = 0
_Metallic ("Metallic", Range(0,1)) = 0.0
}
SubShader
{
Tags { "RenderType"= "Opaque" }
LOD 200
CGPROGRAM
#pragma surface surf Standard fullforwardshadows vertex:vert
#pragma target 3.0
sampler2D _MainTex;
struct Input
{
float2 uv_MainTex;
};
half _Glossiness, _Metallic, _Frequency, _Timer, _WaveLength, _WaveHeight;
fixed4 _Color;
half getHeight(half x, half y)
{
const float PI = 3.14159;
half rad = sqrt(x * x + y * y);
half wavefunc = _WaveHeight * cos(2 * PI * (_Frequency * _Timer - rad / _WaveLength));
return wavefunc;
}
void vert (inout appdata_full v)
{
v.vertex.z -= getHeight(v.vertex.x, v.vertex.y);
}
void surf (Input IN, inout SurfaceOutputStandard o)
{
fixed4 c = tex2D (_MainTex, IN.uv_MainTex) * _Color;
o.Albedo = c.rgb;
o.Metallic = _Metallic;
o.Smoothness = _Glossiness;
o.Alpha = _Color.a;
}
ENDCG
}
FallBack "Diffuse"
}
Your browser does not support HTML5 video.
Волны есть. Но хочется, чтобы анимация начиналась и заканчивалась плоскостью. В этом нам поможет функция синуса. Домножив амплитуду на sin (_Timer * PI) получим плавное появление и исчезновение волн. Так как _Timer принимает значения от 0 до 1, а синус в нуле и в PI равен нулю, это как раз то, что нужно.
Your browser does not support HTML5 video.
Пока совсем не похоже на падение капли. Проблема в том, что энергия волной теряется равномерно. Добавим проперти _Radius, которая будет отвечать за радиус действия эффекта. И домножим на амплитуду clamp (_Radius — rad, 0, 1) и получим уже эффект больше похожий на правду.
Your browser does not support HTML5 video.
Ну и заключительный шаг. То, что амплитуда в каждой отдельной точке достигает своего максимума в момент времени равный 0.5 не совсем верно, эту функцию лучше заменить.

Тут мне стало немного лень считать, и я просто домножил синус на (1 — _Timer) и получил такую кривую.
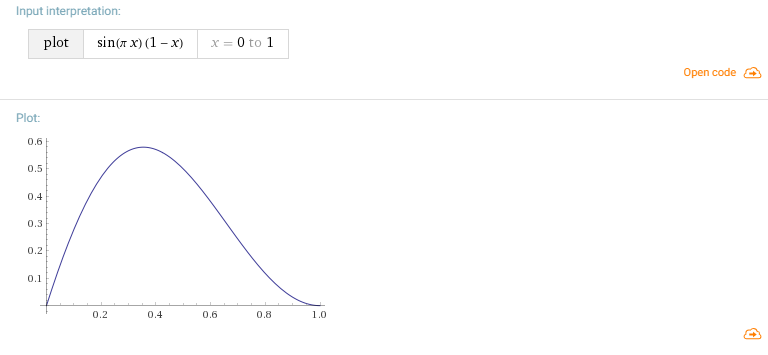
Но в общем с точки зрения математики тут так же можно подобрать нужную кривую исходя из логики в какой момент времени вы хотите пик и примерную форму, а дальше построить интерполяцию по этим точкам.
В итоге получился такой шейдер и эффект.
Shader "CGDevs/Rain/RainRipple"
{
Properties
{
_WaveHeight("Wave Height", float) = 1
_WaveLength("Wave Length", float) = 1
_Frequency("Frequency", float) = 1
_Radius("Radius", float) = 1
_Timer("Timer", Range(0,1)) = 0
_Color ("Color", Color) = (1,1,1,1)
_MainTex ("Albedo (RGB)", 2D) = "white" {}
_Glossiness ("Smoothness", Range(0,1)) = 0
_Metallic ("Metallic", Range(0,1)) = 0.0
}
SubShader
{
Tags { "RenderType"= "Opaque" }
LOD 200
CGPROGRAM
#pragma surface surf Standard fullforwardshadows vertex:vert
#pragma target 3.0
sampler2D _MainTex;
struct Input
{
float2 uv_MainTex;
};
half _Glossiness, _Metallic, _Frequency, _Timer, _WaveLength, _WaveHeight, _Radius;
fixed4 _Color;
half getHeight(half x, half y)
{
const float PI = 3.14159;
half rad = sqrt(x * x + y * y);
half wavefunc = _WaveHeight * sin(_Timer * PI) * (1 - _Timer) * clamp(_Radius - rad, 0, 1)
* cos(2 * PI * (_Frequency * _Timer - rad / _WaveLength));
return wavefunc;
}
void vert (inout appdata_full v)
{
v.vertex.z -= getHeight(v.vertex.x, v.vertex.y);
}
void surf (Input IN, inout SurfaceOutputStandard o)
{
fixed4 c = tex2D (_MainTex, IN.uv_MainTex) * _Color;
o.Albedo = c.rgb;
o.Metallic = _Metallic;
o.Smoothness = _Glossiness;
o.Alpha = _Color.a;
}
ENDCG
}
FallBack "Diffuse"
}
Your browser does not support HTML5 video.
Сетка меша — это важно
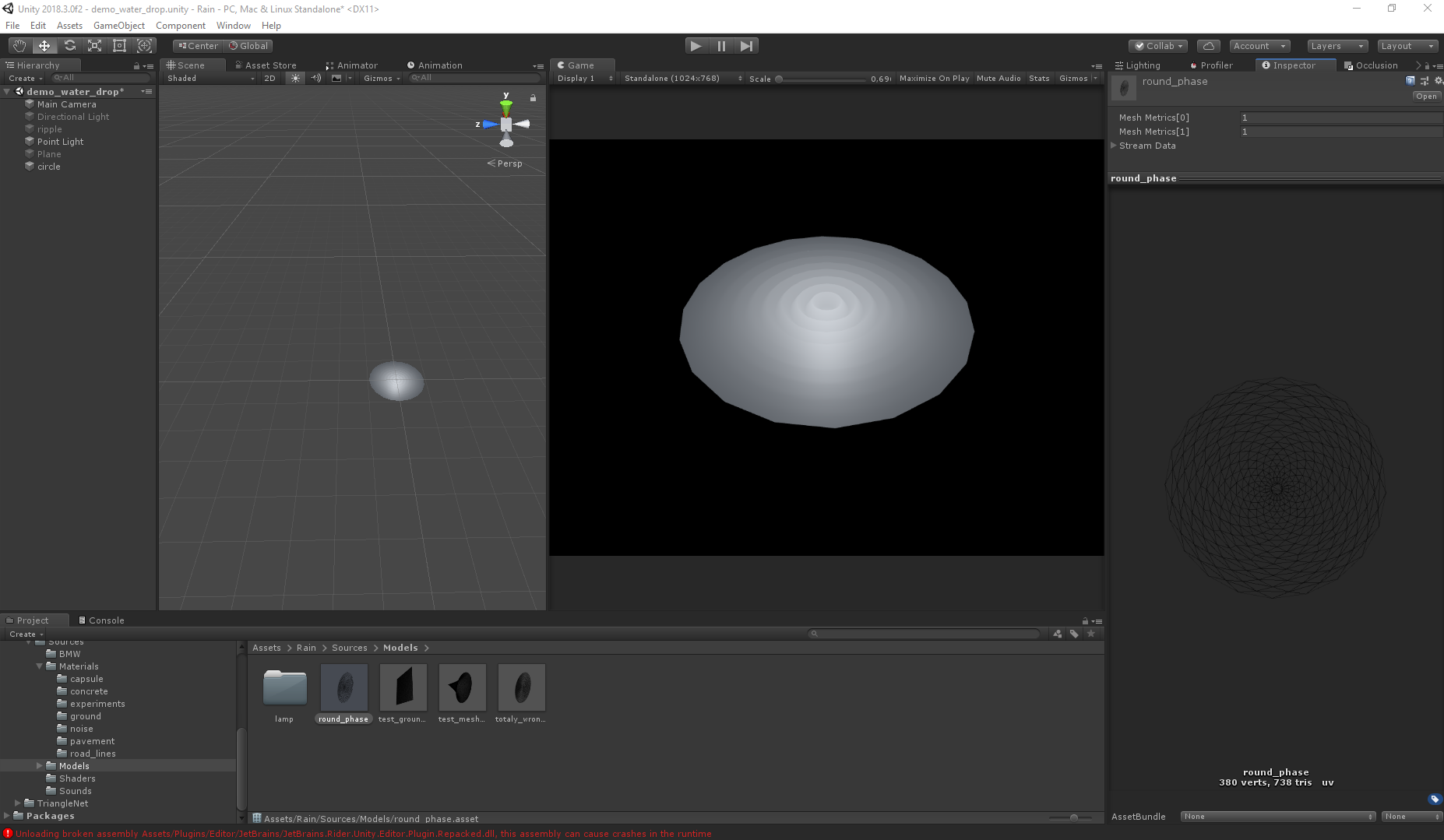
Возвращаясь немного к теме предыдущей статьи. Волны реализованы вертексным шейдером, поэтому сетка меша играет достаточно большую роль. Так как известна природа движения задача упрощается, но в целом от формы сетки зависит финальный визуал. Разница становится не существенной при высокой полигональности, но для производительности чем меньше полигонов, тем лучше. Ниже картинки, иллюстрирующие разницу между сетками и визуалом.
Правильно:
Неправильно:
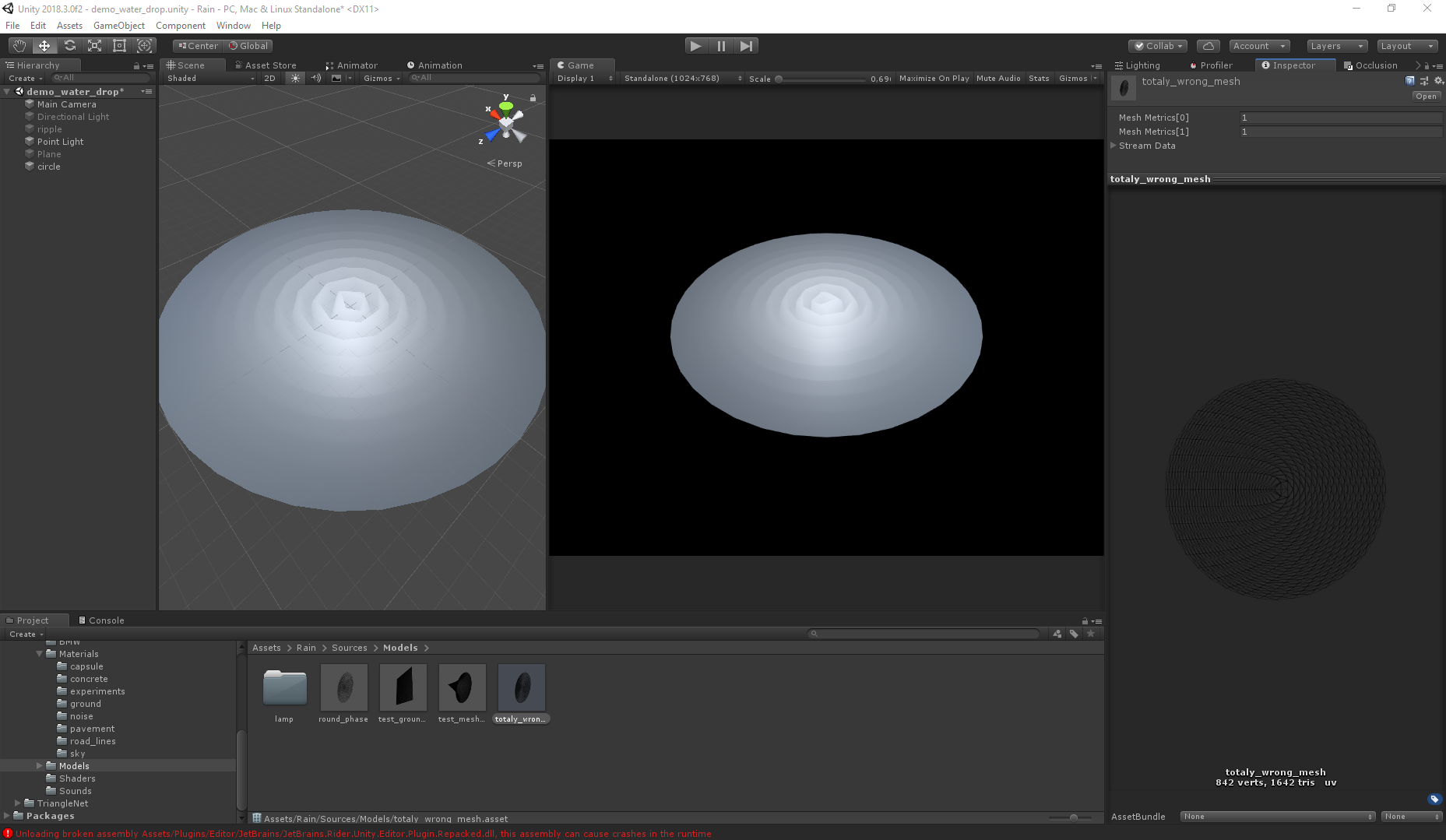
Даже при вдвое большем числе полигонов второй меш даёт неправильный визуал (оба меша сгенерированы с помощь Triangle.Net, просто по разным алгоритмам).
Финальный визуал
В другую версию шейдера добавлена специальная часть для создания волн не строго в центре, а в нескольких точках. То, как это реализовано и каким образом можно передавать подобные параметры я может расскажу в следующих статьях, если тема интересна.
Вот сам шейдер:
Shader "CGDevs/Rain/Ripple Vertex with Pole"
{
Properties
{
_MainTex ("Albedo (RGB)", 2D) = "white" {}
_Normal ("Bump Map", 2D) = "white" {}
_Roughness ("Metallic", 2D) = "white" {}
_Occlusion ("Occlusion", 2D) = "white" {}
_PoleTexture("PoleTexture", 2D) = "white" {}
_Color ("Color", Color) = (1,1,1,1)
_Glossiness ("Smoothness", Range(0,1)) = 0
_WaveMaxHeight("Wave Max Height", float) = 1
_WaveMaxLength("Wave Length", float) = 1
_Frequency("Frequency", float) = 1
_Timer("Timer", Range(0,1)) = 0
}
SubShader
{
Tags {
"IgnoreProjector" = "True"
"RenderType" = "Opaque"}
LOD 200
CGPROGRAM
#pragma surface surf Standard fullforwardshadows vertex:vert
#pragma target 3.0
sampler2D _PoleTexture, _MainTex, _Normal, _Roughness, _Occlusion;
half _Glossiness, _WaveMaxHeight, _Frequency, _Timer, _WaveMaxLength, _RefractionK;
fixed4 _Color;
struct Input
{
float2 uv_MainTex;
};
half getHeight(half x, half y, half offetX, half offetY, half radius, half phase)
{
const float PI = 3.14159;
half timer = _Timer + phase;
half rad = sqrt((x - offetX) * (x - offetX) + (y - offetY) * (y - offetY));
half A = _WaveMaxHeight
* sin(_Timer * PI) * (1 - _Timer)
* (1 - timer) * radius;
half wavefunc = cos(2 * PI * (_Frequency * timer - rad / _WaveMaxLength));
return A * wavefunc;
}
void vert (inout appdata_full v)
{
float4 poleParams = tex2Dlod (_PoleTexture, float4(v.texcoord.xy, 0, 0));
v.vertex.z += getHeight(v.vertex.x, v.vertex.y, (poleParams.r - 0.5) * 2, (poleParams.g - 0.5) * 2, poleParams.b , poleParams.a);
}
void surf (Input IN, inout SurfaceOutputStandard o)
{
o.Albedo = tex2D(_MainTex, IN.uv_MainTex).rgb * _Color.rgb;
o.Normal = UnpackNormal(tex2D(_Normal, IN.uv_MainTex));
o.Metallic = tex2D(_Roughness, IN.uv_MainTex).rgb;
o.Occlusion = tex2D(_Occlusion, IN.uv_MainTex).rgb;
o.Smoothness = _Glossiness;
o.Alpha = _Color.a;
}
ENDCG
}
FallBack "Diffuse"
}
С проектом в целом и тем, как это работает можно ознакомиться тут. Правда часть ресурсов пришлось убрать из-за ограничений по весу гитхаба (hdr skybox и машина).
Спасибо за внимание! Надеюсь, статья будет кому-то полезна, и стало чуть понятнее зачем может понадобится тригонометрия, аналитическая геометрия (всё что связано с кривыми) и другие математические дисциплины.
