Математические основы биткойн-блокчейна
Сегодня биткойн продолжает набирать популярность, а индустрия разрабатывать все новые приложения для работы с криптовалютой. Одной из причин такой популярности является строгая математическая база, на которой строится биткойн.
Благодаря этому система функционирует в условиях полного отсутствия доверия между участниками сети, исключая воздействие человеческого фактора.
Поэтому в сегодняшней статье мы бы хотели поговорить о математических основах биткойн-блокчейна — эллиптических кривых, ECDSA и ключах.
 / Изображение Hernán Piñera CC BY
/ Изображение Hernán Piñera CC BY
Фундаментальной частью биткойна являются криптографические алгоритмы. В частности, алгоритм ECDSA — Elliptic Curve Digital Signature Algorithm, который использует эллиптические кривые (elliptic curve) и конечные поля (finite field) для подписи данных, чтобы третья сторона могла подтвердить аутентичность подписи, исключив возможность её подделки. В ECDSA для подписи и верификации используются разные процедуры, состоящие из нескольких арифметических операций.
Эллиптические кривые
Эллиптическая кривая над полем K — это кубическая кривая над алгебраическим замыканием поля K, задаваемая уравнением третьей степени с коэффициентами из поля K и «точкой на бесконечности». Одной из форм эллиптических кривых являются кривые Вейерштрасса.
y² = x³ + ax + b
Для коэффициентов a = 0 и b = 7 (используемых в биткойне), график функции принимает следующий вид:
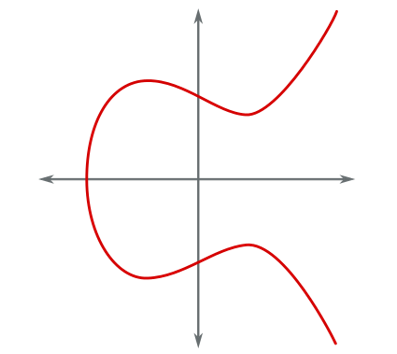
Эллиптическая кривая
Эллиптические кривые имеют несколько интересных свойств, например, невертикальная линия, пересекающая две некасательные точки на кривой, пересечет третью точку на кривой. Суммой двух точек на кривой P + Q называется точка R, которая является отражением точки -R (построенной путем продолжения прямой (P; Q) до пересечения с кривой) относительно оси X.
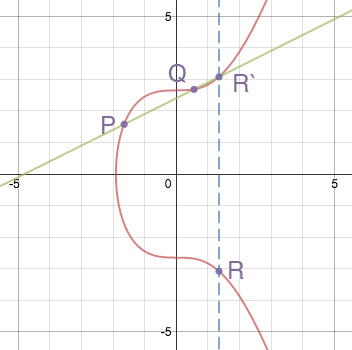
Сумма двух точек на кривой (источник)
Если же провести прямую через две точки, имеющие координаты вида P (a, b) и Q (a, -b), то она будет параллельна оси ординат. В этом случае не будет третьей точки пересечения. Чтобы решить эту проблему, вводится так называемая точка на бесконечности (point of infinity), обозначаемая как O. Поэтому, если пересечение отсутствует, уравнение принимает следующий вид P + Q = O.
Если мы хотим сложить точку саму с собой (удвоить её), то в этом случае просто проводится касательная к точке Q. Полученная точка пересечения отражается симметрично относительно оси X.
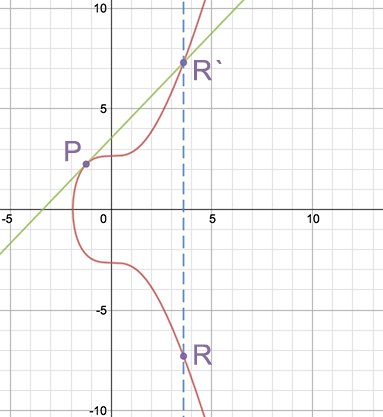
Удвоение точки (источник)
Эти операции позволяют провести скалярное умножение точки R = k*P, складывая точку P саму с собой k раз. Однако отметим, что для работы с большими числами используются более быстрые методы.
Эллиптическая кривая над конечным полем
В эллиптической криптографии (ECC) используется такая же кривая, только рассматриваемая над некоторым конечным полем. Конечное поле в контексте ECC можно представить как предопределенный набор положительных чисел, в котором должен оказываться результат каждого вычисления.
y² = x³ + ax + b (mod p)
Например, 9 mod 7 = 2. Здесь мы имеем конечное поле от 0 до 6, и все операции по модулю 7, над каким бы числом они ни осуществлялись, дадут результат, попадающий в этот диапазон.
Все названные выше свойства (сложение, умножение, точка в бесконечности) для такой функции остаются в силе, хотя график этой кривой не будет походить на эллиптическую кривую. Эллиптическая кривая биткойна, y² = x³ + 7, определенная на конечном поле по модулю 67, выглядит следующим образом:

Эллиптическая кривая биткойна, определенная на конечном поле по модулю 67 (источник)
Это множество точек, в которых все значения х и у представляют собой целые числа между 0 и 66. Прямые линии, нарисованные на этом графике, теперь будут как бы «оборачиваться» вокруг поля, как только достигнут барьера 67, и продолжатся с другого его конца, сохраняя прежний наклон, но со сдвигом. Например, сложение точек (2, 22) и (6, 25) в этом конкретном случае выглядит так:

Сложение точек (2, 22) и (6, 25) (источник)
Если хотите посмотреть, как выглядят другие эллиптические кривые, то поэкспериментировать можно на этом сайте.
ECDSA в биткойне
В протоколе биткойна зафиксирован набор параметров для эллиптической кривой и её конечного поля, чтобы каждый пользователь использовал строго определенный набор уравнений. Среди зафиксированных параметров выделяют уравнение кривой (equation), значение модуля поля (prime modulo), базовую точку на кривой (base point) и порядок базовой точки (order). О вычислении порядка базовой точки вы можете почитать здесь. Этот параметр подбирается специально и является очень большим простым числом.
В случае биткойна используются следующие значения:
Уравнение эллиптической кривой: y² = x³ + 7
Простой модуль: 2256 — 232 — 29 — 28 — 27 — 26 — 24 — 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
Базовая точка:
04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
Жирным шрифтом выделена координата X в шестнадцатеричной записи. За ней сразу следует координата Y.
Порядок: FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
Этот набор параметров для эллиптической кривой известен как secp256k1 и является частью семейства стандартов SEC (Standards for Efficient Cryptography), предлагаемых для использования в криптографии. В биткойне кривая secp256k1 используется совместно с алгоритмом цифровой подписи ECDSA (elliptic curve digital signature algorithm). В ECDSA секретный ключ — это случайное число между единицей и значением порядка. Открытый ключ формируется на основании секретного: последний умножается на значение базовой точки. Уравнение имеет следующий вид:
Открытый ключ = секретный ключ * G
Это показывает, что максимальное количество секретных ключей (следовательно, биткойн-адресов) — конечно, и равняется порядку. Однако порядок является невероятно большим числом, так что случайно или намеренно подобрать секретный ключ другого пользователя нереально.
Вычисление открытого ключа выполняется с помощью тех же операций удвоения и сложения точек. Это тривиальная задача, которую обычный персональный компьютер или смартфон решает за миллисекунды. А вот обратная задача (получение секретного ключа по публичному) — является проблемой дискретного логарифмирования, которая считается вычислительно сложной (хотя строгого доказательства этому факту нет). Лучшие известные алгоритмы ее решения, вроде ро Полларда, имеют экспоненциальную сложность. Для secp256k1, чтобы решить задачу, нужно порядка 2128 операций, что потребует времени вычисления на обычном компьютере, сопоставимого со временем существования Вселенной.
Когда пара секретный/публичный ключ получена, её можно использовать для подписи данных. Эти данные могут быть любой длины. Обычно первым шагом выполняется хеширование данных с целью получения уникального значения с числом битов, равным битности порядка кривой (256). После хеширования, алгоритм подписи данных z выглядит следующим образом. Здесь, G — базовая точка, n — порядок, а d — секретный ключ.
- Выбирается некоторое целое k в пределах от 1 до n-1
- Рассчитывается точка (х, у) = k * G с использованием скалярного умножения
- Находится r = х mod n. Если r = 0, то возврат к шагу 1
- Находится s = (z + r * d) / k mod n. Если s = 0, то возврат к шагу 1
- Полученная пара (r, s) является нашей подписью
После получения данных и подписи к ним, третья сторона, зная публичный ключ, может их верифицировать. Шаги для проверки подписи такие (Q — открытый ключ):
- Проверка, что и r, и s находятся в диапазоне от 1 до n-1
- Рассчитывается w = s-1 mod n
- Рассчитывается u = z * w mod n
- Рассчитывается v = r * w mod n
- Рассчитывается точка (x, y) = uG + vQ
- Если r = x mod n, то подпись верна, иначе — недействительна
В самом деле,
uG + vQ = u + vdG = (u + vd)G = (zs-1 + rds-1)G = (z + rd) s-1G = kG
Последнее равенство использует определение s на этапе создания подписи.
Безопасность ECDSA связана со сложностью задачи поиска секретного ключа, описанной выше. Помимо этого, безопасность исходной схемы зависит от «случайности» выбора k при создании подписи. Если одно и то же значение k использовать более одного раза, то из подписей можно извлечь секретный ключ, что и произошло с PlayStation 3. Поэтому современные реализации ECDSA, в том числе используемые в большинстве биткойн-кошельков, генерируют k детерминировано на основе секретного ключа и подписываемого сообщения.
