Математическая модель радиотелескопа со сверхдлинной базой01.07.2019 18:34

Введение


Одним из первых радиотелескоп построил американец Грот Рёбер в 1937 году. Радиотелескоп представлял собой жестяное зеркало диаметром 9.5 м, установленное на деревянной раме:

wksjqmtr30ljwxkqiuouodyotzq.png

К 1944 году Рёбер составил первую карту распределения космических радиоволн в области Млечного пути.

Развитие радиоастрономии повлекло за собой ряд открытий: в 1946 г. было открыто радиоизлучение из созвездия Лебедь, в 1951 г. — внегалактическое излучение, в 1963 г. — квазары, в 1965 г. открыто реликтовое фоновое излучения на волне 7.5 см.

В 1963 был построен уникальный 300-метровый радиотелескоп в Аресибо (Пуэрто-Рико). Это неподвижная чаша, имеющая перемещающийся облучатель, построена в естественной расщелине местности.

kgkrxolqycfft0qvgbvyxrju-w0.png
Одиночные радиотелескопы имеют небольшое угловое разрешение, которое определяется формулой:
$\Theta=\frac{\lambda }{d}$
где $\lambda$ — длина волны, $d$ — диаметр радиотелескопа.

Очевидно, что для улучшения разрешения необходимо увеличивать диаметр антенны, что физически является трудно реализуемой задачей. Решить ее удалось с появлением радиоинтерферометров.

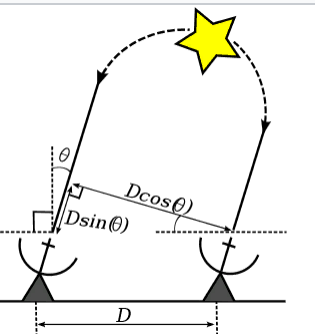
ogoubdstzu2gldmedkmjup8cpmw.png

Фронт электромагнитной волны, излучённой далёкой звездой вблизи Земли, можно считать плоским. В случае самого простого интерферометра, состоящего из двух антенн, разность хода лучей, пришедших на эти две антенны, будет равна:
$\Delta =D\cdot sin(\Theta )$,
где: $\Delta $— разность хода лучей; $D $— расстояние между антеннами; $\Theta $— угол между направлением прихода лучей и нормалью к линии, на которой расположены антенны.

При $\Theta =0 $ волны, пришедшие на обе антенны, суммируются в фазе. В противофазе волны первый раз окажутся при:

$\Delta =\frac{\lambda }{2},\Theta =arcsin\frac{\lambda }{2D}$,
где: $\lambda$— длина волны.

Следующий максимум будет при $\Delta =\lambda, $ минимум при $\Delta =\frac{3\lambda}{2}$ и т. д. Получается многолепестковая диаграмма направленности (ДН), ширина главного лепестка которой при $\lambda<< D$ равна $\lambda/D $. Шириной главного лепестка определяется максимальное угловое разрешение радиоинтерферометра, оно приблизительно равно ширине лепестка.

Радиоинтерферометрия со сверхдлинными базами (РСДБ) — это вид интерферометрии, используемый в радиоастрономии, при котором приёмные элементы интерферометра (телескопы) располагаются не ближе, чем на континентальных расстояниях друг от друга.

Метод РСДБ позволяет объединять наблюдения, совершаемые несколькими телескопами, и тем самым имитировать телескоп, размеры которого равны максимальному расстоянию между исходными телескопами. Угловое разрешение РСДБ в десятки тысяч раз превышает разрешающую силу лучших оптических инструментов.

Современное состояние РСДБ — сетей


Сегодня космос слушают несколько РСДБ — сетей:

  • Европейская –EVN (European VLBI Network), состоящая более чем из 20-ти радиотелескопов;
  • Американская –VLBA (Very Long Baseline Array), включающая десять телескопов диаметром 25 метров каждый;
  • Японская — JVN (Japanese VLBI Network) состоит из десяти антенн, расположенных в Японии, включая четыре астрометрических антенны (проект VERA — VLBI Exploration of Radio Astrometry);
  • Австралийская — LBA (Long Baseline Array);
  • Китайская — CVN (Chinese VLBI Network), состоящая из четырех антенн;
  • Южно Корейская — KVN (Korean VLBI Network), включающая в себя три 21- метровых радиотелескопа;
  • Российская — на основе постоянно действующего радиоинтерферометрического комплекса — «Квазар-КВО» с радиотелескопами диаметром зеркала 32 м, оснащенными высокочувствительными криорадиометрами в диапазоне волн от 1.35 см до 21 см. Длина баз — эффективный диаметр синтезированного «зеркала» — составляет около 4400 км в направлении восток-запад (см.рисунок).


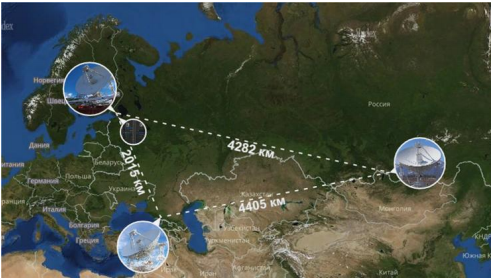
tw3r91nvli5ptiarywugzd-mkxe.png

В РСДБ — комплексе «Квазар-КВО» в качестве источника опорной частоты для всех частотных преобразований применяются водородные стандарты, в которых используется переход между уровнями сверхтонкой структуры основного состояния атома водорода с частотой 1420.405 МГц, соответствующей в радиоастрономии линии 21 см.

Задачи, решаемые средствами РСДБ


  • Астрофизика. Выполняется построение радиоизображений естественных космических объектов (квазаров и других объектов) с разрешением десятые и сотые доли mas (миллисекунд дуги).
  • Астрометрические исследования. Построение координатновременных систем. Объектами исследований являются радиоисточники чрезвычайно малых угловых размеров, включая квазизвездные радиоисточники и ядра радиогалактик, которые из-за большой удаленности являются почти идеальными объектами для создания сети опорных неподвижных объектов.
  • Исследования по небесной механике и динамике солнечной системы, космической навигации. Установление радиомаяка на поверхностях планет и слежение за радиомаяками межпланетных автоматических станций позволяет использовать метод РСДБ для исследования таких параметров, как орбитальное движение планеты, направление осей вращения и их прецессию, динамику системы планета спутник. Для Луны решается также весьма важная задача определения физической либрации и определения динамики систем Луна — Земля.


Навигация в космосе средствами РСДБ


  • Контроль перемещений астронавтов по лунной поверхности в 1971 г. Передвигались они с помощью лунохода «Ровер». Точность определения его положения относительно лунного модуля достигала 20 см и зависела в основном от либрации луны (Либрация- периодические маятникообразные колебания Луны относительно ее центра масс);
  • Навигационное сопровождение доставки и сброса аэростатных зондов с пролетных аппаратов в атмосферу Венеры (проект ВЕГА). Расстояние до Венеры составляет более 100 млн. км, мощность передатчиков всего 1 Вт. Запуски аппаратов ВЕГА-½ состоялись в декабре 1984 г. Аэростаты были сброшены в атмосферу Венеры 11 и 15 июня 1985 г. Наблюдение велось в течение 46 часов.


Структурная схема упрощенной РСДБ — сети


На основе реальной РСДБ — сети, используя программные средства Python, промоделируем упрощенную систему РСДБ в виде отдельных моделей для каждого блока или процесса. Данной совокупности моделей будет достаточно для наблюдения основных процессов. Структурная схема упрощенной РСДБ — сети представлена на рисунке:

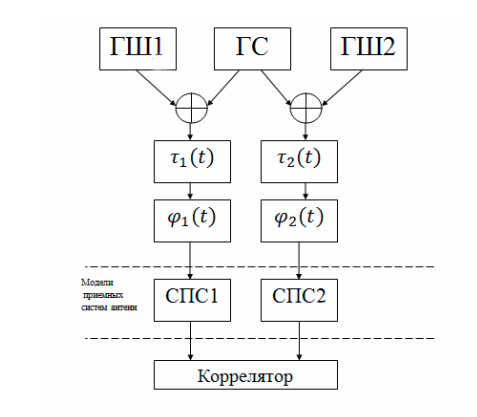
-frwcx2tlnvlm_ay5jhoaqo3qe4.png

Система включает следующие компоненты:

  • генератор полезного фазомодулированного сигнала (ГС);
  • генераторы шума (ГШ1, ГШ2). В системе имеются два радиотелескопа (приемные антенны), которые имеют собственные шумы. Кроме того, существуют шумы атмосферы и других естественных и искусственных источников радиоизлучения;
  • блок задержки по времени, имитирующий линейно меняющуюся во времени задержку, обусловленную вращением Земли;
  • фазовращатель, моделирующий эффект Доплера;
  • система преобразования сигналов (СПС), состоящая из гетеродина, для переноса сигнала вниз по частоте, и полосового фильтра;
  • FX-коррелятор.


Схема коррелятора приведена на следующем рисунке:

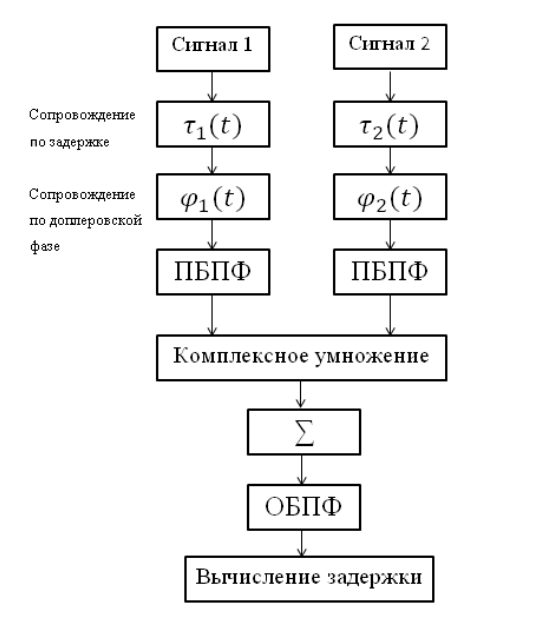
mauulhoapod1j9vth5soltzcjmg.png

Приведенная схема коррелятора, который включает в себя следующие блоки:

  • прямого быстрого преобразования Фурье (ПБПФ) и обратного преобразования Фурье (ОБПФ);
  • компенсирующий ранее внесенную задержку;
  • компенсирующий эффект Доплера;
  • комплексного перемножения двух спектров;
  • суммирования накопленных реализаций.


Модель навигационных сигналов


Наиболее удобными для РСДБ- измерений являются навигационные сигналы космических аппаратов спутниковых навигационных систем, таких как GPS и ГЛОНАСС. К навигационным сигналам предъявляется ряд требований:

  • позволять хорошо определять псевдодальность;
  • передавать информацию о положении навигационной системы;
  • быть отличимым от сигналов других НС;
  • не создавать помех другим радиосистемам;
  • не требовать для приема и передачи сложной аппаратуры.


В достаточной мере им удовлетворяет сигнал с бинарной (двухпозиционной) фазовой модуляцией — BPSK (binary phase shift key), которая в русскоязычной литературе обозначается ФМ-2. Эта модуляция меняет фазу несущего колебания, на π, что можно представить в виде:

$S(t)=A\cdot G(t)\cdot cos(2\pi ft),$

где G (t)– модулирующая функция.

Для реализации фазовой модуляции можно использовать два генератора, каждый из которых формирует одну и ту же частоту, но с различной начальной фазой. Модулирующая функция позволяет расширить спектр сигнала и точно измерить псевдодальность (расстояние между спутником и приемником, вычисленное по времени распространения сигнала без поправки за расхождение часов спутника и приемника).

Приведу листинг, поясняющий основные принципы BPSK:

Листинг
from scipy import*
from pylab import*
import numpy as np
import scaleogram as scg 
f = 2; #fчастота синусоиды
fs = 100; #период дискретизации синусоидальной волны
t = arange(0,1,1/fs) #разбить время на сегменты 1 / fs
#установка фазовых сдвигов для разных сигналов BPSK
p1 = 0;
p2 = pi;
#получить количество битов для модуляции
N =12#ведите количество битов для модуляции
#генерирование случайного сигнала
bit_stream=np.random.random_integers(0, 1, N+1)
#выделение динамических переменных
time =[];
digital_signal =[];
PSK =[];
carrier_signal =[];
#ПОЛУЧЕНИЕ СИГНАЛОВ
for ii in arange(1,N+1,1):
    #оригинальный цифровой сигнал
    if bit_stream [ii] == 0:
        bit = [0 for w in arange(1,len(t)+1,1)];
    else:
       bit = [1 for w in arange(1,len(t)+1,1)];
    digital_signal=hstack([digital_signal,bit ])
    #Генерация сигнала BPSK
    if bit_stream [ii] == 0:
        bit = sin (2*pi*f*t+p1);
    else:
        bit = sin (2*pi*f*t+p2);
    PSK=hstack([PSK,bit])
    #Генерация несущей волны
    carrier = sin (2*f*t*pi);
    carrier_signal = hstack([carrier_signal,carrier]) ;
    time = hstack([time ,t]);
    t=t+1
suptitle("Сигналы двоичной фазовой модуляции (BPSK)")   
subplot (3,1,1);
plot(time,digital_signal,'r');
grid();
subplot (3,1,2);
plot (time,PSK);
grid();
subplot (3,1,3);
plot (time,carrier_signal);
grid()
show()
figure()
title("Спектр сигнала двоичной фазовой модуляции (BPSK)")
n = len(PSK) 
k = np.arange(n)
T = n/fs
frq = k/T
frq = frq[np.arange(int(n/2))] 
Y = fft(PSK)/n 
Y = Y[range(n //2)] / max(Y[range(n // 2)])
plot(frq[75:150], abs(Y)[75:150], 'b')#Выбор окна Фурье преобразования
grid()
#Скалограмма вейвлет преобразования PSK  сигнала
scales = scg.periods2scales( arange(1, 40))
ax2 = scg.cws(PSK, scales=scales, figsize=(6.9,2.9));
show()


Получим:

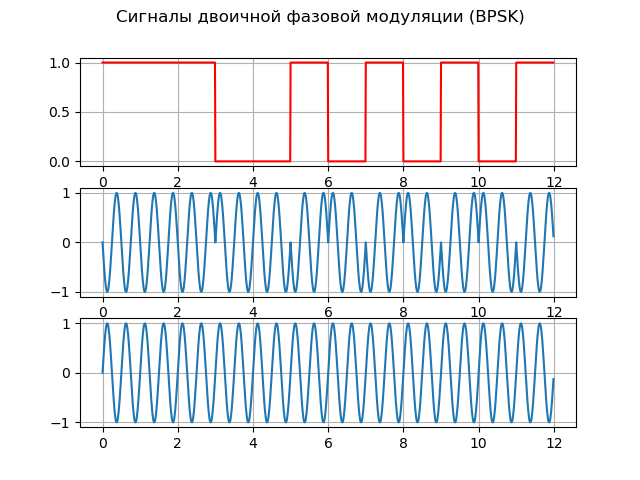
8u9z5auwncjt8lo8rark1rjlnby.png

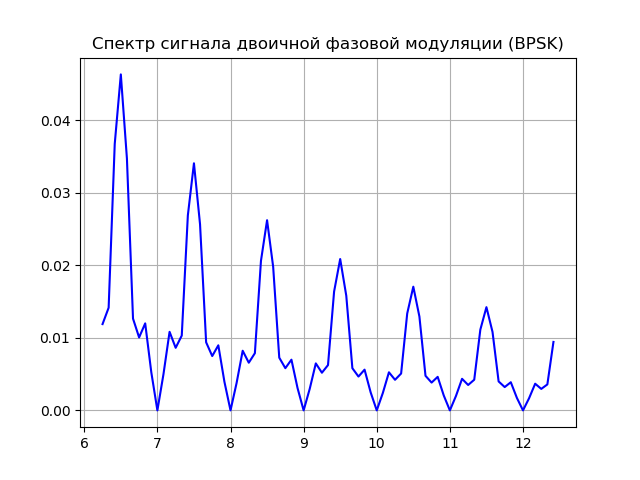
wxgseqqoujmfc3v-g2uswapmy8y.png

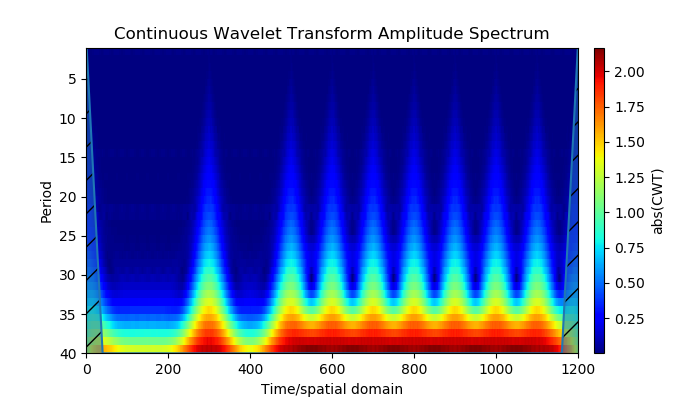
q60msa4d5inprz4wgvktd6zfes4.png

Модель источников сигналов


Навигационный фазомодулированный гармонический сигнал от спутника или космического аппарата имеет вид:

$x=a(2\pi f_{c}t+\sum s_{n} cos(2\pi f_{n}t)),$

где частота несущего колебания $f_{c}=8,4 $ ГГц.

У сигнала есть несколько управляемых параметров: амплитуда n-го модулирующего колебания
$s_{n}, $ его частота $f_{c}$ и амплитуда несущего колебания a.

Для получения корреляционной функции, в которой будут максимально подавлены её боковые лепестки и достигнут наиболее узкий корреляционный пик, мы будем варьировать значения частот, используя значения 2, 4, 8 и 16 МГц, и индекса модуляции в пределах от 0 до 2π с шагом π. Приведу листинг программы для такого поиска параметров фазомодулированной функции для конечного результата:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7 #длительность одной реализации
N = 2**18 #кол-во отсчетов
delay =4 #задержка
t1 =linspace(0, T, N)
t2 = linspace(0 + delay, T + delay, N)
fs = (N - 1)/T #частота дискретизации
ax = 1e-3
bx = 2e-6
ay = 2e-3
by = 3e-6
aex = 1e-3 + 30e-9
bex = 2e-6 + 10e-12
aey = 2e-3 + 30e-9
bey = 3e-6 + 10e-12
taux = ax + bx*t1
tauy = ay + by*t2
tauex = aex + bex*t1
tauey = aey + bey*t2
#амплитуда шума
# print("амплитуда шума:")
No1 = No2 = 0
fc = 8.4e9 #частота сигнала
#амплитуды модулирующих колебаний
A1 = 2*pi
A2 = 0
A3 =2*pi
A4 = 4*pi
# модулирующие частоты
fm1 = 2e6
fm2 = 4e6
fm3 = 8e6
fm4 = 16e6
f = 20e6 # центральная частота на НЧ
ff = fc - f # частота гетеродина
fco = 16e6 #частота среза относительно центральной частоты
def korel(x,y):
    #эффект доплера
    def phase_shifter1(x, t, tau, b):
     L = linspace(0, N, N)
     fexp = ifftshift((L) - ceil((N - 1)/2))/T
     s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t)
     return s
    #компенсация эффекта доплера
    def phase_shifter2(x, t, tau, b):
     L = linspace(0,N,N)
     fexp = ifftshift((L) - ceil((N - 1)/2))/T
     s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t)
     return s
    #гетеродинирование
    def heterodyning(x, t):
     return x*exp(-1j*2*pi*ff*t)
    #фильтрация
    def filt(S): 
     p = signal.convolve(S,h)
     y = p[int((n - 1)/2) : int(N+(n - 1)/2)]
     return y
    def corr(y1, y2):
     Y1 = fft(y1)
     Y2 = fft(y2)
     #свертка
     Z = Y1*Y2.conjugate()
     #ОПФ
     z = ifft(Z)/N
     return sqrt(z.real**2 + z.imag**2)
    #построение графика КФ
    def graf(c, t):
        c1=c[int(N/2):N]
        c2=c[0:int(N/2)]
        C = concatenate((c1, c2))
        xlabel('Время,с')
        ylabel('Амплитуда')
        title('Оптимальная корреляционная функция ')
        grid(True)
        plot(t*1e9 - 250, C, 'b',label=" Подавлены боковые лепестки \n и сужен главный лепесток")
        legend(loc='best')
        show()
    noise1 = random.uniform(-No1, No1, size = N) #шум первого сигнала
    noise2 =noise1 #шум второго сигнала   
    x1 = heterodyning(phase_shifter1(x + noise1, t1, taux, bx), t1)
    y1 = heterodyning(phase_shifter1(y + noise2, t2, tauy, by), t2)
    n = 100001 #порядок фильтра
    #ИХ фильтра
    h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False)
    x2 = filt(x1)
    y2 = filt(y1)
    X2 = phase_shifter2(x2, t1, tauex, bex)
    Y2 = phase_shifter2(y2, t2, tauey, bey)
    Corr = corr(X2, Y2)
    graf(Corr, t1)
#Влияние одной компоненты модулирующего колебания
##for A1 in [pi/4,pi/2,pi]:   
##    x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1))
##    y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2))
##    korel(x,y)     
##for fm in [ fm2,fm3,fm4]:
##    A1=2*pi
##    x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm*t1))
##    y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm*t2))
##    korel(x,y)
#Влияние двух компонент модулирующего колебания
##for fm2 in [ fm1, fm2,fm3,fm4]:
##    A1=2*pi
##    A2=2*pi
##    fm1=2e6
##    x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)+A2*np.cos(2*pi*fm2*t1))
##    y =cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2)+A2*np.cos(2*pi*fm2*t2))
##    korel(x,y)    
x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)+A2*np.cos(2*pi*fm2*t1)+A3*cos(2*pi*fm3*t1)+A4*cos(2*pi*fm4*t1))
y =  cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2) +A2*cos(2*pi*fm2*t2) +A3*cos(2*pi*fm3*t2)+A4*cos(2*pi*fm4*t2))
korel(x,y)


Получим:

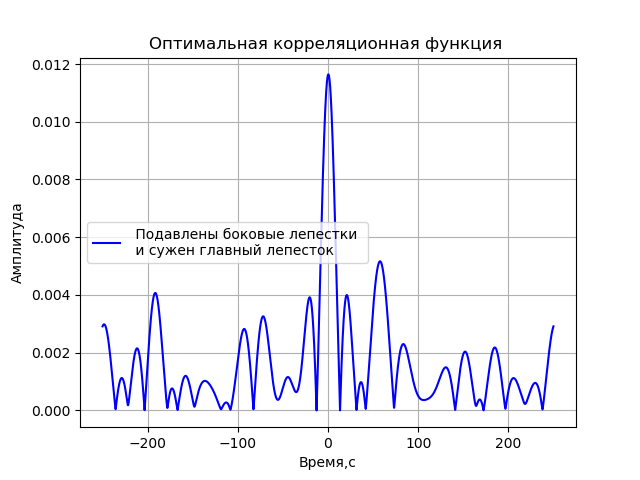
aszo3gdkn_fl0bymm1ebfgez-qm.png

Полученная функция имеет вид:

$x=cos(2\pi f_{c}t+2\pi cos(2\pi 10^{6}t)+2\pi cos(2\pi 10^{8}t)+4\pi cos(2\pi 10^{16}t)). (1)$

Далее указанная функция будет использоваться для моделирования РСДБ.

Модель генератора шума, имитирующего помехи, принимаемые вместе с сигналом из космоса и из атмосферы Земли


Функция (1) фазомодулированного навигационного сигнала может быть применена к обоим каналам радиоинтерферометра, но при этом нужно учитывать задержку сигнала во втором канале и шум в обоих каналах как показано в следующем листинге:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7 #длительность одной реализации
N = 2**16 #кол-во отсчетов
delay =1e-7  #задержка
t1 =linspace(0, T, N)
t2 = linspace(0 + delay, T + delay, N)
fc = 8.4e9 #частота сигнала
# print("амплитуда шума:")
No1 = No2 = 0.5
noise1 = random.uniform(-No1, No1, size = N) #шум первого сигнала
noise2 =random.uniform(-No1, No1, size = N) #шум второго сигнала
x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2))
title("Имитация равномерно распределённого шума \n в навигационных каналах РСДБ")
plot(t1,x,label=" Первый канал")
plot(t2,y,label="Второй канал c задержкой")
x=noise1;y=noise2 
plot(t1,x,label="Шум первого канала")
plot(t2,y,label="Шум второго канала")
legend(loc='best')
grid(True)
figure()
noise1_2 = np.random.uniform(-No1, No1, size = N) #шум первого и второго сигнала
sko=np.std(noise1_2)
mo= np.mean(noise1_2)
sko=round(sko,2)
mo=round(mo,2)
title("Гистограмма исследуемого шума. СКО:%s,МО:%s"%(sko,mo))
ylabel('Частота попадания в интервал')
xlabel('Интерваал возможных значений')
hist(noise1_2,bins='auto')
show()


Получим:

-kkomcpvrq63rzhuj6qroo2cisy.png

Задержка delay =1e-7 установлена для демонстрации, в реальности она зависит от базы и может достигать четырёх и более единиц.

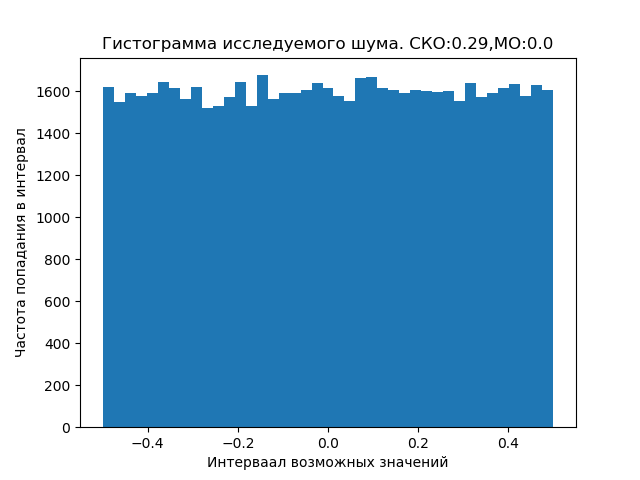
bye82dhuipgcrlhyjrcg4dpryg4.png

Шумы как космические, так и околоземные могут быть распределены по закону отличного от приведенного равномерного, что требует специальных исследований.

Моделирование эффекта Доплера


В связи с тем, что Земля имеет округлую форму и вращается вокруг своей оси, то сигналы из космоса поступают на антенны с разными задержками. По этой причине требуется сдвинуть сигналы по времени и учесть доплеровскую частоту. Приближено будем считать, что задержка меняется по линейному закону:

$\tau _{x}(t)=a_{x}+b_{x}t, (2)$

где $a_{x}=1..3\cdot 10^{-3}$ мс, а $b_{x}=1..3\cdot 10^{-6}$ мс. Доплеровская фаза находится, как производная от задержки:

$f_{dx}=\frac{d\tau(t)}{dt}=b_{x}, (3)$

Принимаемый сигнал должен иметь вид:

$\hat{x}=x(t-\tau _{x})e^{j2\pi f_{dx}t},$
где x (t) — излучаемый сигнал космического аппарата.

Демонстрация эффекта Доплера приведена в следующем листинге:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7#длительность одной реализации
N = 2**16 #кол-во отсчетов
t1 =linspace(0, T, N)
delay =4 #задержка
t2 = linspace(0 + delay, T + delay, N)
fc = 8.4e9#частота сигнала
def phase_shifter1(x, t, tau, b):
 L = linspace(0, N, N)
 fexp = ifftshift((L) - ceil((N - 1)/2))/T
 s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t)
 return s.real
figure()
title("Эффект Доплера для первого канала")
ax = 3e-3
bx = 3e-6
taux = ax + bx*t1
x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
sx=phase_shifter1(x, t1, taux, bx )
plot(t1[0:150],x[0:150],label=" Сигнал первого канала без эффекта Доплера")
plot(t1[0:150],sx[0:150],label=" Сигнал первого канала с эффектом Доплера")
grid(True)
legend(loc='best')
figure()
title("Эффект Доплера для второго канала")
ay = 2e-3
by = 3e-6
tauy = ay + by*t2
y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2))
sy= phase_shifter1(y, t2, tauy, by)
plot(t2[0:150],y[0:150],label=" Сигнал  второго канала без эффекта Доплера")
plot(t2[0:150],sy[0:150],label=" Сигнал второго канала с эффектом Доплера")
grid(True)
legend(loc='best')
show()


Получим:

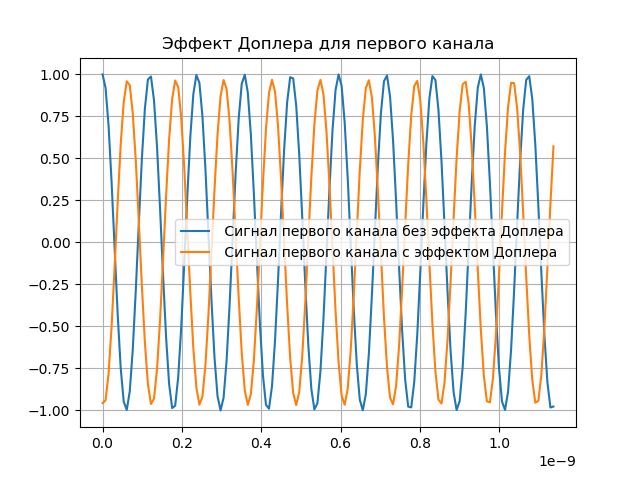
ymvxx5hul9ilsqwodmokczio7lu.png

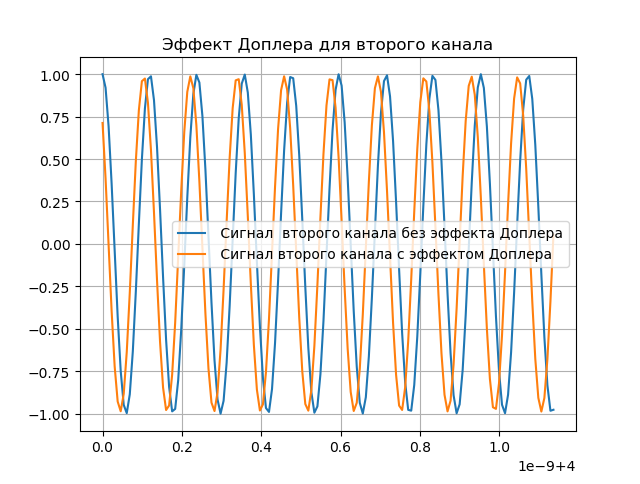
qutiymujlnjnkf3cl6n_wfuwute.png

Моделирование компенсации эффекта Доплера


Очевидно, что внесенные в сигнал изменения должны быть компенсированы. Для этой цели в системе присутствует сопровождение по задержке и доплеровской фазе. После прохождения сигналом системы регистрации, вносится задержка:

$\tau _{ex}(t)=a_{x}+b_{ex}t, (4)$

Будет считать, что задержка рассчитывается с определенной точностью, такой что $\left | a_{ex}-a_{x} \right |< 30 $ нс $\left | b_{ex}-b_{x} \right |< 10 $ нс, т.е. она будет немного отличаться он внесенной ранее задержки. Понятно, что задержка вносится с противоположным знаком, чем внесенная ранее.

Полученный сигнал будет иметь вид:

$\hat{x}=\tilde{x}(t+\tau _{ex})e^{-j2\pi f_{de}t}. (5)$

Компенсация эффекта Доплера приведена в следующем листинге:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7#длительность одной реализации
N = 2**16 #кол-во отсчетов
t1 =linspace(0, T, N)
delay =4 #задержка
t2 = linspace(0 + delay, T + delay, N)
fc = 8.4e9#частота сигнала
def phase_shifter1(x, t, tau, b):
 L = linspace(0, N, N)
 fexp = ifftshift((L) - ceil((N - 1)/2))/T
 s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t)
 return s.real
ax = 3e-3
bx = 3e-6
taux = ax + bx*t1
x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
sx=phase_shifter1(x, t1, taux, bx )
ay = 2e-3
by = 3e-6
tauy = ay + by*t2
y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2))
sy= phase_shifter1(y, t2, tauy, by)
def phase_shifter2(x, t, tau, b):
 L = linspace(0,N,N)
 fexp = ifftshift((L) - ceil((N - 1)/2))/T
 s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t)
 return s.real
figure()
title("Компенсация эффекта Доплера для первого канала")
aex = 1e-3 + 30e-9
bex = 2e-6 + 10e-12
tauex = aex + bex*t1
x1 = phase_shifter2(sx, t1, tauex, bex)
plot(t1[0:150],x1[0:150],label=" Сигнал первого канала без эффекта Доплера")
grid(True)
legend(loc='best')
figure()
title("Компенсация эффекта Доплера для  второго канала")
aey = 2e-3 + 30e-9
bey = 3e-6 + 10e-12
tauey = aey + bey*t2
y2 = phase_shifter2(sy, t2, tauey, bey)
plot(t2[0:150],y2[0:150],label=" Сигнал второго канала без эффекта Доплера")
grid(True)
legend(loc='best')
show()


Получим:

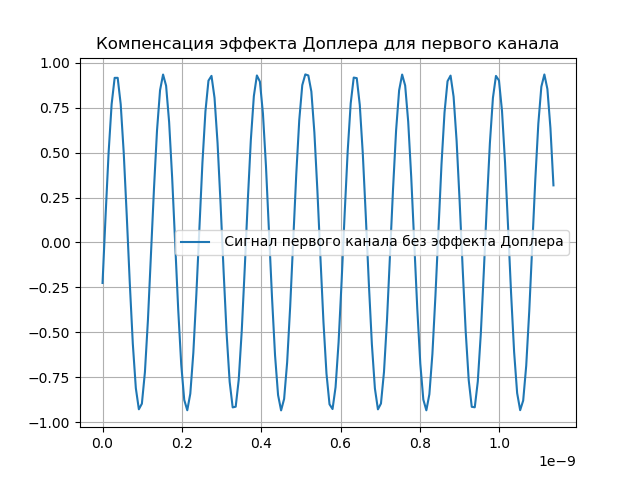
hf691jrzcl7nmupwirozoxasqgs.png

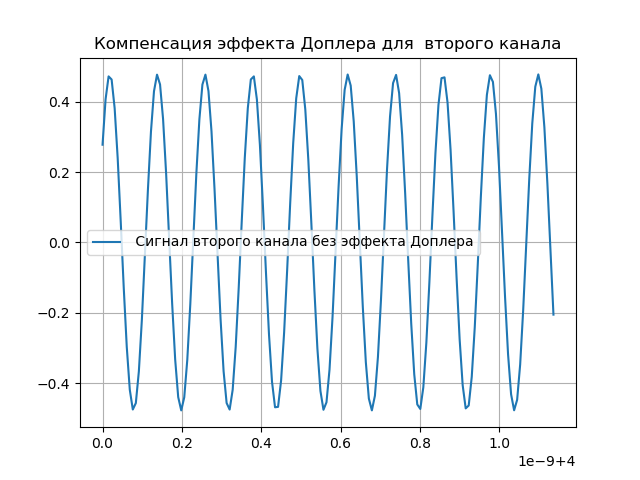
eor3n4ocb_gxz-zbdmxtojbms78.png

Моделирование гетеродинирования сигнала


После попадания сигнала в систему регистрации происходит преобразование частоты, которое так же называют гетеродинированием. Это нелинейное преобразование, при котором из сигналов двух различных частот $f_{1} $и $f_{2}$ выделяется сигнал разностной частоты — $f=\left | f_{1} -f_{2}\right .| $Частота сигнала гетеродина будет равна разности между частотой исследуемого сигнала и частотой, которую требуется получить после переноса. Осуществляется гетеродинирование с помощью вспомогательного генератора гармонических колебаний — гетеродина и нелинейного элемента. Математически гетеродинирование представляет собой умножение сигнала на экспоненту:

$x_{g}=\hat{x}e^{j2\pi f_{g}t},(6)$
где $f_{g}$ — сигнал гетеродина.

Программа для гетеродинирования:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7 #длительность одной реализации
N = 2**16 #кол-во отсчетов
t1 =linspace(0, T, N)
fs = (N - 1)/T #частота дискретизации
fc = 8.4e9 #частота сигнала
f = 20e6 # центральная частота на НЧ
ff = fc - f # частота гетеродина
def spectrum_wavelet(y,a,b,c,e,st):# построение спектра
    n = len(y)# длина сигнала
    k = arange(n)
    T = n / a
    frq = k / T  # двухсторонний частотный диапазон
    frq = frq[np.arange(int(n/2))]  # односторонний частотный диапазон
    Y = fft(y)/ n # FFT вычисления и нормализация
    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))])
    plot(frq[b:c],abs(Y)[b:c],e,label=st) # построение спектра
    xlabel('Freq (Hz)')
    ylabel('|Y(freq)|')
    legend(loc='best')
    grid(True)  
x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
a=fs;b=0;c=20000;e='g'; st=' Спектр сигнала до гетеродинирования  '
spectrum_wavelet(x,a,b,c,e,st)
show()


Получим:

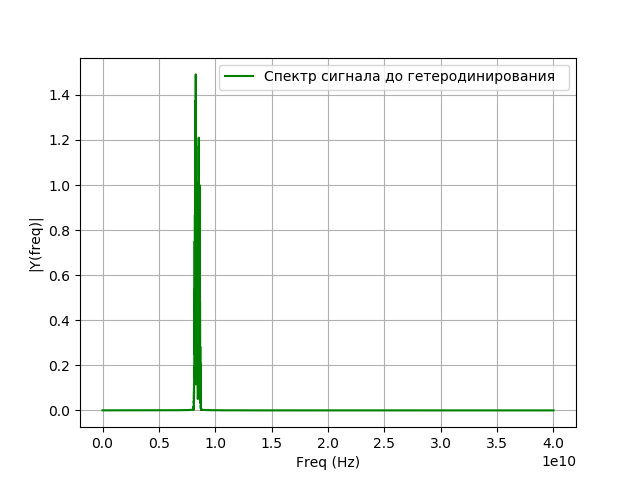
nvkq-ilu-ojd0mwjnaqvs_plhka.png

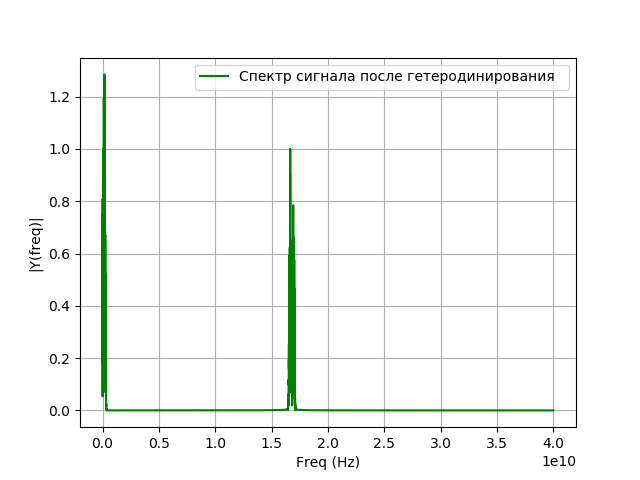
g2x2jlaexxjprhvlwk3zrcntnws.png

Моделирование фильтрации сигнала после гетеродинирования


После гетеродинирования сигнал поступает на полосовой фильтр. Полоса пропускания (ПП) фильтра $f_{pass}=32$ МГц. Импульсная характеристика (ИХ) фильтра рассчитывается оконным методом с помощью библиотечной функции signal.firwin. Для получения сигнала на выходе фильтра, производится свертка ИХ фильтра и сигнала во временной области. Интеграл свертки для нашего случая принимает вид:

$\check{x}(t)=\int_{-\infty }^{+\infty}x_{g}(t)h(t-{t}')dt,(7)$

где h (t) — импульсная характеристика фильтра.

Свертка находится с помощью библиотечной функции signal.convolve. Регистрируемый сигнал с учётом гетеродинирования и фильтрации представлен в виде формулы

$\check{x}(t)=(\hat{x}(t)e^{-j2\pi f_{g}t})*h$

где свертка обозначена знаком *.

Программа для моделирования фильтрации:

Листиннг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7 #длительность одной реализации
N = 2**16 #кол-во отсчетов
t1 =linspace(0, T, N)
fs = (N - 1)/T #частота дискретизации
fc = 8.4e9 #частота сигнала
f = 20e6 # центральная частота на НЧ
ff = fc - f # частота гетеродина
def spectrum_wavelet(y,a,b,c,e,st):# построение спектра
    n = len(y)# длина сигнала
    k = arange(n)
    T = n / a
    frq = k / T  # двухсторонний частотный диапазон
    frq = frq[np.arange(int(n/2))]  # односторонний частотный диапазон
    Y = fft(y)/ n # FFT вычисления и нормализация
    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))])
    plot(frq[b:c],abs(Y)[b:c],e,label=st) # построение спектра
    xlabel('Freq (Hz)')
    ylabel('|Y(freq)|')
    legend(loc='best')
    grid(True)  
x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
def heterodyning(x, t):
     return x*exp(-1j*2*pi*ff*t).real
z=heterodyning(x, t1)
fco = 16e6 #частота среза относительно центральной частоты
n = 100001 #порядок фильтра
h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False)
def filt(S):    
 p = signal.convolve(S,h)
 y = p[int((n - 1)/2) : int(N+(n - 1)/2)]
 return y
q=filt(z)
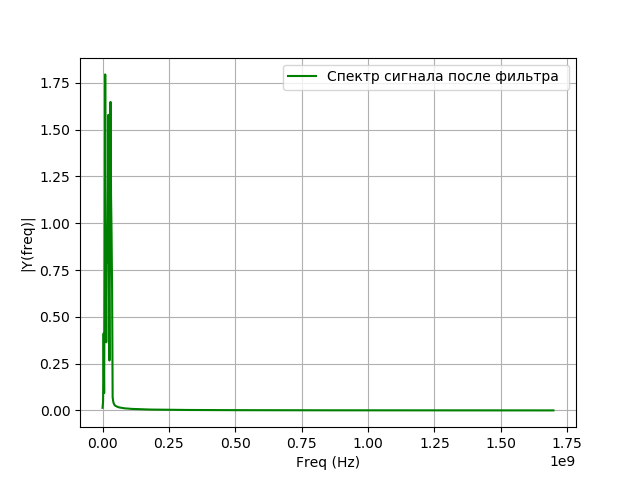
a=fs;b=0;c=850;e='g'; st='Спектр сигнала после фильтра '
spectrum_wavelet(q,a,b,c,e,st)
show()


Получим:

7ku77bi0v2s0jt-gvsqi77rolmw.png

В цифровых преобразователях сигнала для РСДБ в основном используются фильтры с конечной импульсной характеристикой (КИХ), так как они имеют ряд преимуществ по сравнению с фильтрами с бесконечной импульсной характеристикой (БИХ):

  1. КИХ- фильтры могут иметь строго линейную фазовую характеристику в случае симметричности импульсной характеристики (ИХ). Это значит, что используя такой фильтр, можно избежать фазовых искажений, что особенно важно для радиоинтерферометрии. Фильтры с бесконечной импульсной характеристикой (БИХ) не обладают свойствами симметрии ИХ и не могут иметь линейную ФЧХ.
  2. КИХ- фильтры нерекурсивны, а значит — всегда устойчивы. Устойчивость же БИХ -фильтров не всегда можно гарантировать.
  3. Практические последствия того, что для реализации фильтров используется ограниченное число битов, значительно менее существенны для КИХ-фильтров.


В приведенном листинге реализована модель полосового КИХ- фильтра с помощью оконного метода, был подобран порядок фильтра такой, чтобы форма АЧХ фильтра была близка к прямоугольной. Количество коэффициентов смоделированного фильтра n=100001, то есть порядок фильтра P=100000.

Программа для построения АЧХ и ФЧХ полученного КИХ- фильтра:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7 #длительность одной реализации
N = 2**16 #кол-во отсчетов
t1 =linspace(0, T, N)
fs = (N - 1)/T #частота дискретизации
fc = 8.4e9 #частота сигнала
f = 20e6 # центральная частота на НЧ
ff = fc - f # частота гетеродина
fco = 16e6 #частота среза относительно центральной частоты
n = 100001 #порядок фильтра
h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False)
#график ФЧХ
def AFC(A, n, f, deltf, min, max):
    plot((fftfreq (n, 1./fs)/1e9),
    10*log10(abs(fft(A))), 'k')
    axvline((f - fco)/1e9, color = 'red', label='Границы полосы пропускания')
    axvline((f + fco)/1e9, color = 'red')
    axhline(-3, color='green', linestyle='dashdot')
    text(8.381, -3, repr(round(-3, 9)))
    xlabel('Частота, ГГц')
    ylabel('Коэффициент передачи, дБ')
    title('АЧХ')
    grid(True)
    axis([(f - deltf)/1e9, (f + deltf)/1e9, min, max])
    grid(True)
    show()
#график ФЧХ
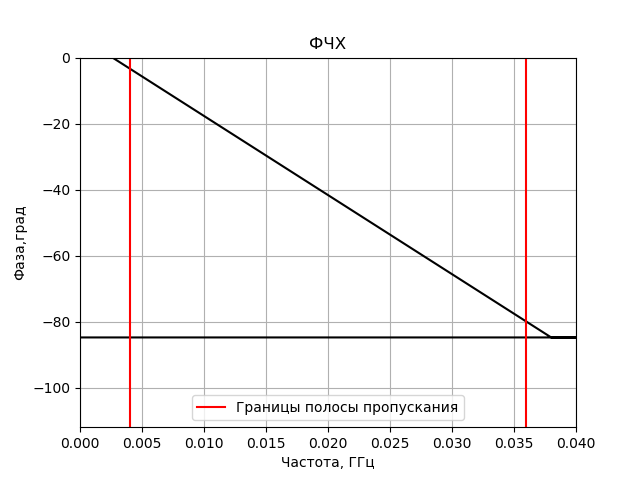
def PFC(A, n, f, deltf, min, max):
    plot(fftfreq(n, 1./fs)/1e9,
    np.unwrap(np.angle(fft(A))), 'k')
    axvline((f - fco)/1e9, color='red', label='Границы полосы пропускания')
    axvline((f + fco)/1e9, color='red')
    xlabel('Частота, ГГц')
    ylabel('Фаза,град')
    title('ФЧХ')
    axis([(f - deltf)/1e9, (f + deltf)/1e9, min, max]) #границы графика
    grid(True)
    legend(loc='best')
    show()
AFC(h, n, f, 20e6, -30, 1)
PFC(h, n, f, 20e6, -112, 0)


Получим:

gljvxx4sd67i0i8_ilsc_u4jnbo.png

dlsqqdgdfv8f_iyf0howpibtkq4.png

Модель FX-коррелятора


Далее каждый сигнал подвергается быстрому Фурье преобразованию (БПФ). БПФ реализуется с помощью библиотечной функции fft из scipy.fftpack. Полученные спектры комплексно- сопряжено умножаются:

$S(j\omega)=S_{1}(j\omega)*S_{2}(j\omega)=(a_{1}+jb_{1})*(a_{2}-jb_{2}) =a_{1}a_{2}+b_{1}b_{2}+j(b_{1}a_{2}-a_{1}b_{2})$

Последнее действие — обратное БПФ. Так как интерес представляет амплитуда корреляционной функции, то полученный сигнал необходимо преобразовать по формуле:

$A=\sqrt{re^{2}+im^{2}}$

Программа для корреляционной функции без учета искажений системы регистрации:

Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7#длительность одной реализации
N = 2**16 #кол-во отсчетов
t1 =linspace(0, T, N)
delay =4 #задержка
t2 = linspace(0 + delay, T + delay, N)
fc = 8.4e9#частота сигнала
def corr(y1, y2):
    Y1 = fft(y1)
    Y2 = fft(y2)
    #свертка
    Z = Y1*Y2.conjugate()
     #ОПФ
    z = ifft(Z)/N
    q=sqrt(z.real**2 + z.imag**2)
    c1=q[int(N/2):N]
    c2=q[0:int(N/2)]
    C = concatenate((c1, c2))
    xlabel('Время,с')
    ylabel('Амплитуда')
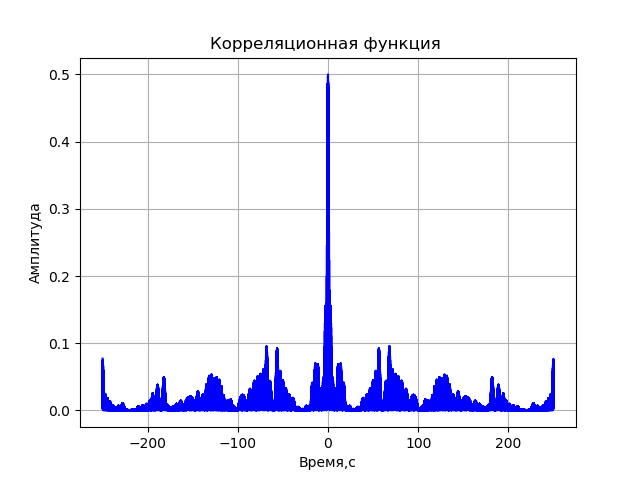
    title('Корреляционная функция ')
    grid(True)
    plot(t1*1e9 - 250, C, 'b')
    show()
x= cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2))
corr(x, y)


Получим:

-bfiq_dqjzvmb2nwbsas7m3ohr4.png

Полный листинг компьютерной модели РСДБ:


Листинг
# coding: utf-8
from pylab import*
from scipy import signal
from scipy import *
T = 5e-7 #длительность одной реализации
N = 2**18 #кол-во отсчетов
delay =4 #задержка
t1 =linspace(0, T, N)
t2 = linspace(0 + delay, T + delay, N)
fs = (N - 1)/T #частота дискретизации
ax = 1e-3
bx = 2e-6
ay = 2e-3
by = 3e-6
aex = 1e-3 + 30e-9
bex = 2e-6 + 10e-12
aey = 2e-3 + 30e-9
bey = 3e-6 + 10e-12
taux = ax + bx*t1
tauy = ay + by*t2
tauex = aex + bex*t1
tauey = aey + bey*t2
#амплитуда шума
# print("амплитуда шума:")
No1 = No2 = 0
# амплитуда несущего колебания
# print("амплитуда сигнала:")
fc = 8.4e9 #частота сигнала
f = 20e6 # центральная частота на НЧ
ff = fc - f # частота гетеродина
fco = 16e6 #частота среза относительно центральной частоты
#эффект Доплера
def phase_shifter1(x, t, tau, b):
 L = linspace(0, N, N)
 fexp = ifftshift((L) - ceil((N - 1)/2))/T
 s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t)
 return s
#компенсация эффекта Доплера
def phase_shifter2(x, t, tau, b):
 L = linspace(0,N,N)
 fexp = ifftshift((L) - ceil((N - 1)/2))/T
 s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t)
 return s
#гетеродинирование
def heterodyning(x, t):
 return x*exp(-1j*2*pi*ff*t)
#фильтрация
def filt(S): 
 p = signal.convolve(S,h)
 y = p[int((n - 1)/2) : int(N+(n - 1)/2)]
 return y
def spectrum_wavelet(y,a,b,c,e,st):# построение спектра
    n = len(y)# длина сигнала
    k = arange(n)
    T = n / a
    frq = k / T  # двухсторонний частотный диапазон
    frq = frq[np.arange(int(n/2))]  # односторонний частотный диапазон
    Y = fft(y)/ n # FFT вычисления и нормализация
    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))])
    plot(frq[b:c],abs(Y)[b:c],e,label=st) # построение спектра
    xlabel('Freq (Hz)')
    ylabel('|Y(freq)|')
    legend(loc='best')
    grid(True)    
def corr(y1, y2):
 Y1 = fft(y1)
 Y2 = fft(y2)
 #свертка
 Z = Y1*Y2.conjugate()
 #ОПФ
 z = ifft(Z)/N
 return sqrt(z.real**2 + z.imag**2)
#построение графика КФ
def graf(c, t):
    c1=c[int(N/2):N]
    c2=c[0:int(N/2)]
    C = concatenate((c1, c2))
    xlabel('Время, с')
    ylabel('Амплитуда')
    title('Корреляционная функция ')
    grid(True)
    plot(t*1e9 - 250, C, 'b')
    show()
noise1 = random.uniform(-No1, No1, size = N) #шум первого сигнала
noise2 =random.uniform(-No1, No1, size = N) #шум второго сигнала
def signal_0():
    x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1))
    y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2))
    return x,y
title("Сигналы + шум +эффект Доплера до фильтра")
x,y= signal_0()
x1 = heterodyning(phase_shifter1(x + noise1, t1, taux, bx), t1)
plot(x1.real,label=" Первый канал")
y1 = heterodyning(phase_shifter1(y + noise2, t2, tauy, by), t2)
plot(y1.real,label="Второй канал")
grid(True)
legend(loc='best')
show()
n = 100001 #порядок фильтра
#ИХ фильтра
h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False)
title("Сигналы- шум- эффект Доплера после фильтра") 
x2 = filt(x1)
plot(x2.real,label=" Первый канал")
y2 = filt(y1)
plot(y2.real,label="  Второй канал")
grid(True)
legend(loc='best')
show()
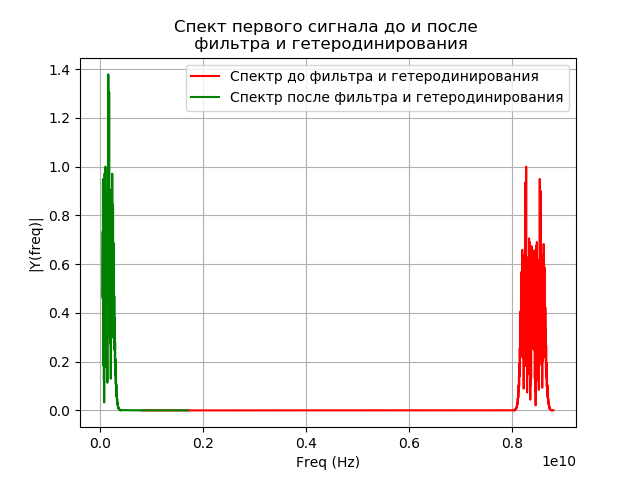
plt.title("Спектр первого сигнала до и после \n фильтра и гетеродинирования") 
a=fs;b=400;c=4400;e='r'
st="Спектр до фильтра и гетеродинирования"
spectrum_wavelet(x,a,b,c,e,st)
a=fs;b=20;c=850;e='g'
st="Спектр после фильтра и гетеродинирования"
spectrum_wavelet(x1,a,b,c,e,st)
show()
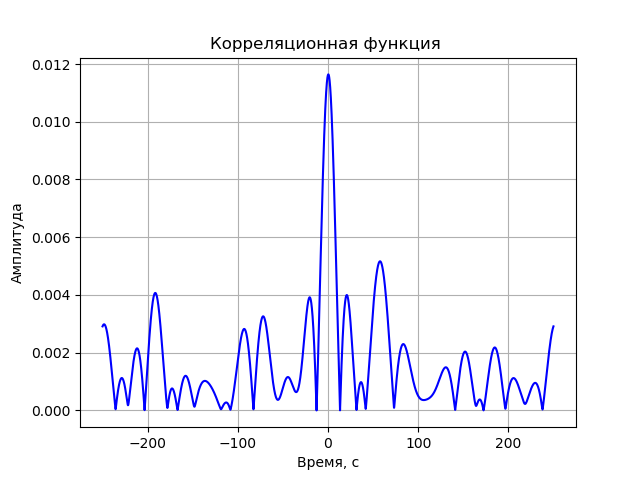
X2 = phase_shifter2(x2, t1, tauex, bex)
Y2 = phase_shifter2(y2, t2, tauey, bey)
Corr = corr(X2, Y2)
graf(Corr, t1)


Получим: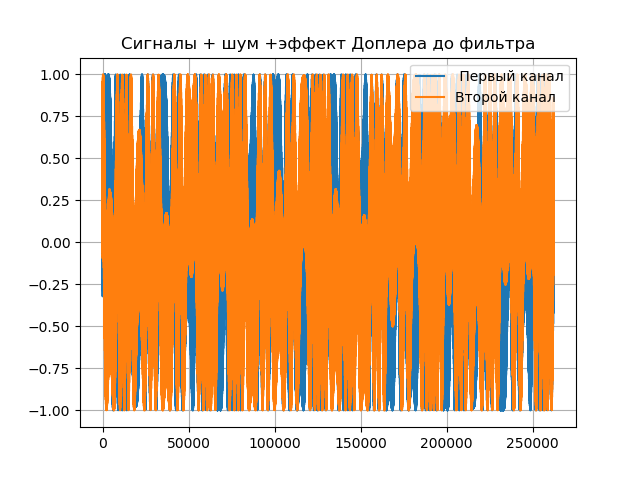
zzbk6igxrx9kkng1apvihgvyjri.png
kty_vxqr_dkkyim1syemov3u_ns.png
qhxpbibvhz1h1eze0jajkicghrg.png
xonimdtpkpzb4fs1kwoqaoznmjo.png

Выводы


  1. Приведена краткая история развития радиоастрономии.
  2. Проанализировано современное состояние РСДБ — сетей.
  3. Рассмотрены задачи, решаемые средствами РСДБ– сетей.
  4. Средствами Python построена модель навигационных сигналов с бинарной (двухпозиционной) фазовой модуляцией — BPSK (binary phase shift key). В модели использован вейвлет анализ фазовой модуляции.
  5. Получена модель источников сигналов, позволяющая определить параметры модуляции, обеспечивающие оптимальную корреляционную функцию по критерию подавления боковых лепестков и максимальной амплитуды центрального лепестка.
  6. Получена модель упрощенной РСДБ — сети, учитывающая шумы и эффект Доплера. Рассмотрены особенности фильтрации с использованием фильтра с конечной импульсной характеристикой.
  7. После краткого изложения теории все модели снабжены демонстрационными программами, позволяющими отслеживать влияние параметров модели.

© Habrahabr.ru