Машинное обучение — 1. Корреляция и регрессия. Пример: конверсия посетителей сайта
Как и обещал, начинаю цикл статей по «машинному обучению». Эта будет посвящена таким понятиям из статистики, как корреляция случайных величин и линейная регрессия. Рассмотрим, как реальные данные, так и модельные (симуляцию Монте-Карло).Часть 1. Реальные данныеЧтобы было интереснее, рассказ построен на примерах, причем в качестве данных (и в этой, и в следующих, статьях) я буду стараться брать статистику прямо отсюда, с Хабра. А именно, неделю назад я написал свою первую статью на Хабре (про Mathcad Express, в котором и будем все считать). И вот теперь статистику по ее просмотрам за 10 дней и предлагаю в качестве исходных данных. На графике это ряд Views, синяя линия. Второй ряд данных (Regs, с коэффициентом 100) показывает число читателей, выполнивших после прочтения определенное действие (регистрацию и скачивание дистрибутива Mathcad Prime).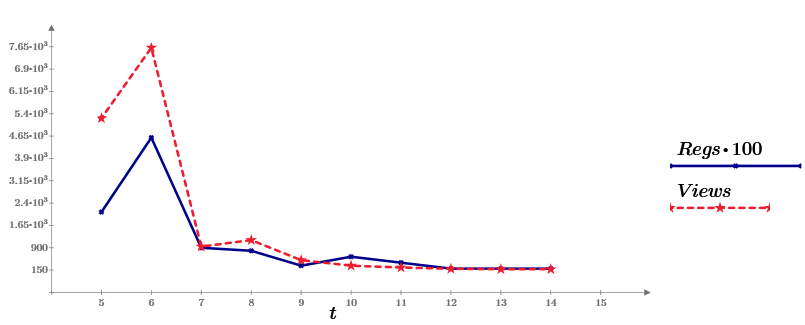
Так уж получилось, что у меня, кроме статистики просмотра статьи (с Хабра), был доступ к статистике скачиваний Mathcad (по ссылке, которую я дал внутри текста статьи). Таким образом, у нас все есть для того, чтобы разобраться с таким понятием интернет-маркетинга, как конверсия. Конверсией обычно называют отношение числа посетителей сайта, выполнивших на нём покупку, регистрацию или т.п. к общему числу посетителей. Например: в первый день публикации мою статья была просмотрена 5 тыс. раз, а скачиваний было 20, т.е. конверсия составила 0.4%.
Все картинки — это скриншоты Mathcad Express (сами расчеты можете взять здесь, повторить, а при желании изменить и использовать для своих нужд). Исходные данные (три вектора) я ввел руками:

Вот расчеты конверсии (в %): «мгновенной» (для каждого дня) и «средней» (за 10 дней). Любопытно, что значение конверсии немного «плывет» со временем (от 0.4% в первый день до квази-стационарного 1% в последние дни), что, само по себе, достойно обсуждения (которое отложим до следующих статей — про случайные процессы и время корреляции).
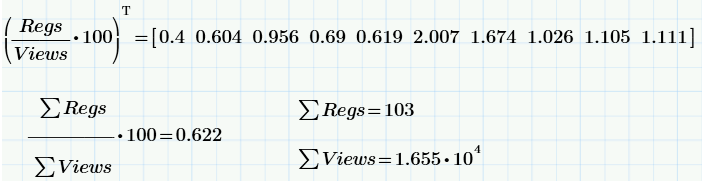
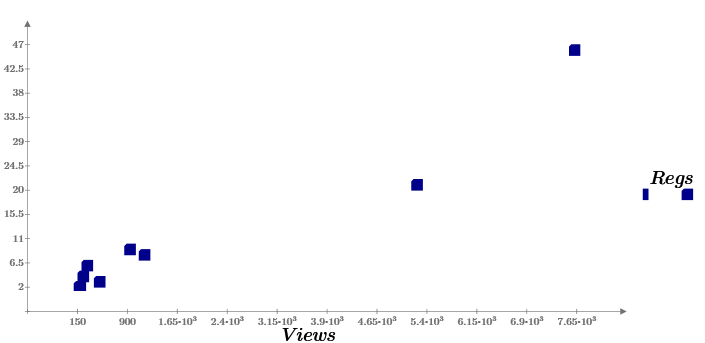
Тот очевидный факт, что число целевых действий (скачиваний) зависит от числа просмотров, наглядно продемонстрирует график Regs (Views). Мы видим, что, хотя и число просмотров, и число скачиваний — случайные, тем не менее они связаны между собой (почти) линейной зависимостью.
Теперь немного «школьной» статистики: вычисление (по определению) среднего значения, дисперсии и коэффициента корреляции двух выборок Views и Regs.
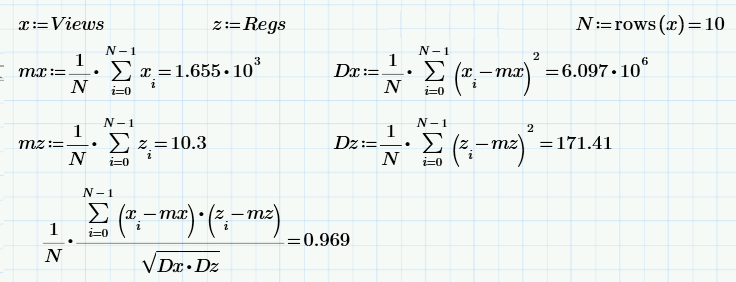
Последняя формула — это вычисление коэффициента корреляции — меры того, насколько зависимыми являются две случайные величины (точнее, меры линейной зависимости). Получается, что выборочное значение коэффициента корреляции равно 0.97. Это очень много (что, впрочем, и неудивительно, по самой постановке задачи).
Наконец, решим задачу математической регрессии — приближения, в общем случае, выборки данных (x, z) определенной функцией f (x), определенным образом минимизирующей совокупность ошибок f (x)-z. Самый простой и наиболее часто используемый вид регрессии — линейная, когда f (x)=A*x+B. Еще линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты A и B вычисляются обычно из условия минимизации суммы квадратов ошибок:
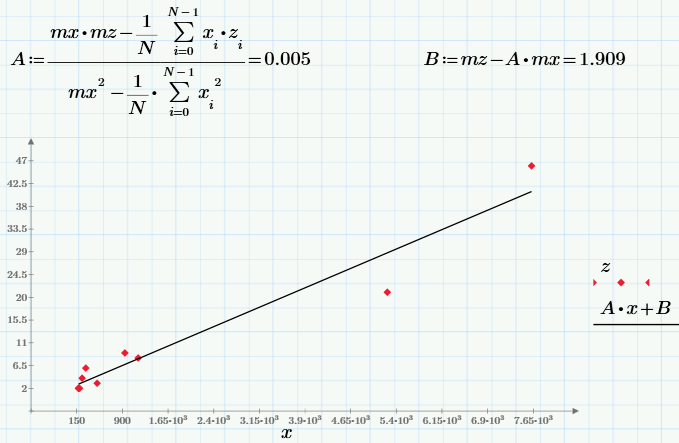
К слову, метод наименьших квадратов (минимизация суммы квадратов ошибок) — не единственно возможный вариант построения регрессии. Например, иногда применяется медиан-медианная линейная регрессия.
Наконец, о том, для чего нужна регрессия в нашей задаче. Если принять линейный характер зависимости скачиваний от просмотров, то коэффициент А как раз и будет характеризовать конверсию. Судя по нему, конверсия равна 0.005=0.5%, т.е., если, к примеру, у нас есть маркетинговая цель — достичь показателя 100 скачиваний, то, исходя из модели линейной регрессии, нам надо «залить» на сайт 100/0.005=20 тыс. просмотров.
Часть 2. Моделирование Монте-Карло
В то время как в прошлой части мы оперировали случайными данными, полученными в ходе эксперимента, в заключение повторим те же расчеты при помощи датчика псевдослучайных чисел. В методах Монте-Карло часто требуется создавать случайные числа с определенной корреляцией. Для начала сгенерируем три псевдослучайных массива: х и y — независимые, а z — зависящий от х (с «генеральным» значением коэффициента корреляции r): 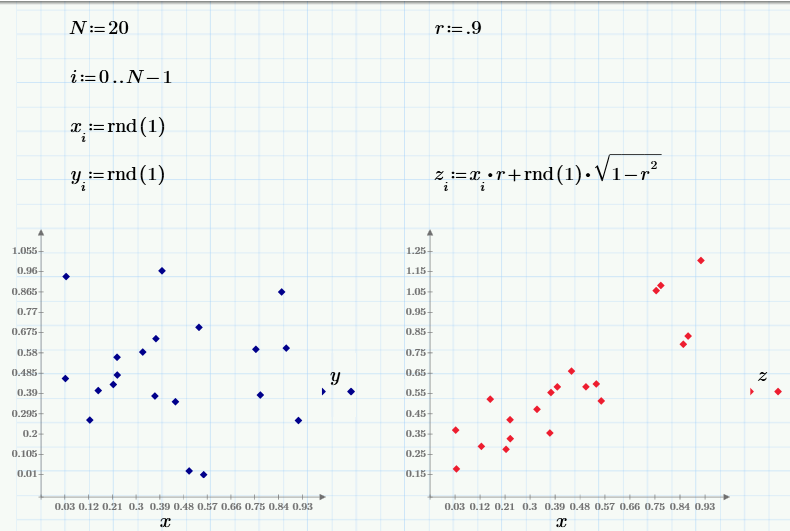
На графике слева показана зависимость некоррелированых случайных значений х и y, а справа — зависимость коррелированых z и х.
Используя те же формулы, что в прошлом разделе, получим статистические характеристики выборок х, y и z (в том числе, выборочное значение коэффициента корреляции):
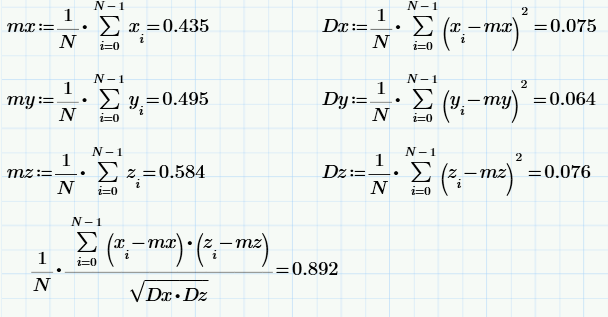
Ну, и, наконец, по формуле метода наименьших квадратов построим линейную регрессию z=A*x+B:
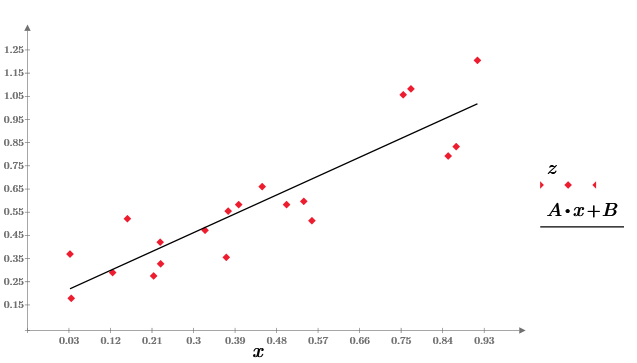
Заинтересовавшимся читателям оставляю поэкспериментировать с параметром r и посмотреть, как его изменение будет влиять на зависимость z (x). Еще любопытно, изменяя объем выборки N, следить за результатом расчета статистических характеристик.
Ссылки:
Видеокурс «Машинное обучение» (ШАД Яндекса) Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani. An Introduction to Statistical Learning in R (PDF) Trevor Hastie, Robert Tibshirani, Jerome Friedman. The Elements of Statistical Learning (PDF)
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
