Макраме из света: шифрование данных на оптических узлах

Научные изыскания позволяют нам не только лучше понимать окружающий наш мир, но и контролировать некоторые процессы и явления. За долгие годы исследований и экспериментов мы научились менять свойства материалов, манипулировать электромагнитными полями, видеть далекие планеты и звезды, разбирать по кирпичикам клетки и многое другое. Некоторые новообретенные умения сильно удивили бы ученых прошлого. Одним из таких умений является возможность менять форму луча света. Но как это применить на практике? Ученые из Оттавского университета (Оттава, США) предложили создать обрамленный оптический узел, который можно использовать для хранения и кодирования информации. Как ученые завязывали луч света в узел, каковы свойства такой структуры и насколько безопасно хранить данные на оптических узлах? На эти и другие вопросы мы найдем ответы в докладе ученых. Поехали.
Основа исследования
Любой моряк, дайвер или альпинист скажет, что правильный узел может спасти жизнь. Мастера макраме превратили узлы в настоящее искусство. А тайна наушников, самостоятельно запутывающихся в узлы, до сих пор остается не раскрыта.
Как мы прекрасно знаем, любой объект или процесс поддается математическому описанию, и узлы не исключение. С точки зрения математики, узел это вложение окружности в трехмерное евклидово пространство.
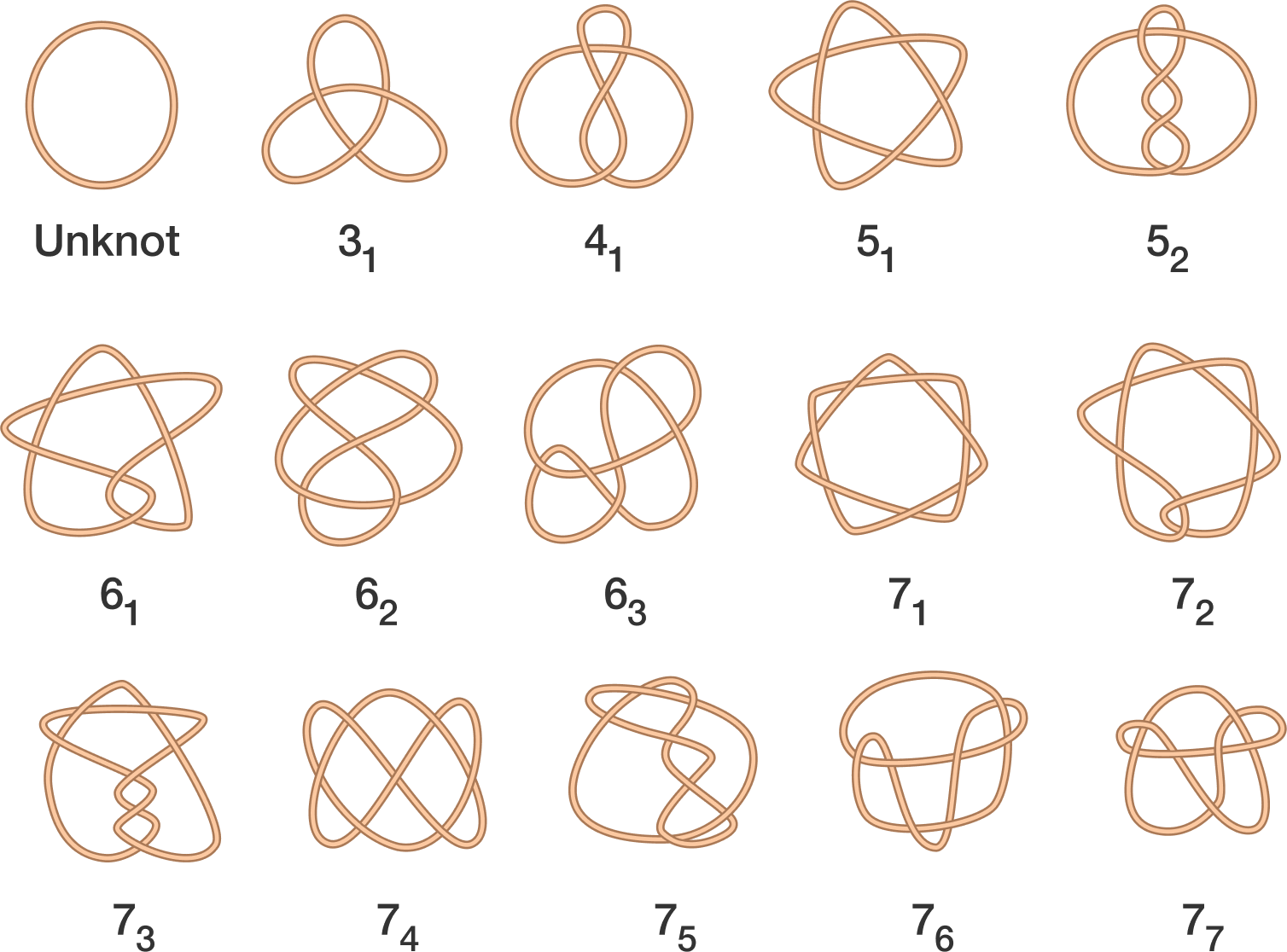
Типы простых узлов.
Математическая классификация узлов достаточно обширна (трилистник, печать Соломона, узел Листинга и т.д.). В данном же исследовании был задействован особый вид узлов — обрамленный. Такой узел создается из плоской ленты. Грубо говоря, это своего рода запутанная лента Мебиуса.
Вторым компонентом исследования, естественно, был свет, а именно структурированный свет, представляющий собой оптическое поле с определенными пространственными и временными особенностями, которые можно менять. Как напоминают ученые, создание таких структур в основном опирается на концепции, связанные с сингулярной оптикой, т.е. изучение неоднородностей в оптических волновых полях. Неоднородности, которые можно найти в оптических фазах или в поляризации, именуются оптическими сингулярностями. Их можно использовать для создания оптических лучей разной сложности: от лучей с единственной сингулярностью до волновых полей, образующих топологические полосы и узлы.
К числу последних как раз и относится ранее упомянутая лента Мебиуса, а также разные типы узлов. Проблема в том, что подобные структуры часто рассматриваются как двумерные, нежели трехмерные, т.е. как оптические лучи с единственной сингулярностью.
В рассматриваемом нами сегодня исследовании ученые решили исправить этот недочет, экспериментально продемонстрировав генерацию и работу структур в волновых полях оптической поляризации, образующих обрамленные узлы. Кроме того, созданные узлы были использованы для кодирования топологической информации посредством совместного использования факторизации простых чисел и собственных топологических инвариантов узлов.
Создание оптического обрамленного узла
Узел, как мы уже знаем, это описание того, как запутанные нити/линии/полосы расположены в пространстве. По этой причине при анализе в рамках физической структуры узлы обычно обнаруживаются в полях, определяемых областями, которые однозначно образуют кривые в трехмерном пространстве. Такие узловые кривые были продемонстрированы в таких системах, как вихри в жидкостях, нули интенсивности в скалярных оптических полях и в пределах C-линий оптических полей поляризации.
C-линии, в частности, состоят из кривых чистой круговой поляризации в монохроматических электромагнитных полях. Одна из их самых отличительных особенностей связана со структурой поляризационного поля в непосредственной близости от них. Если точнее, то они заключены в поляризационные эллипсы с большой осью, которая вращается на целые числа, кратные π, вдоль замкнутого контура, окружающего C-линию (1а и 1d).
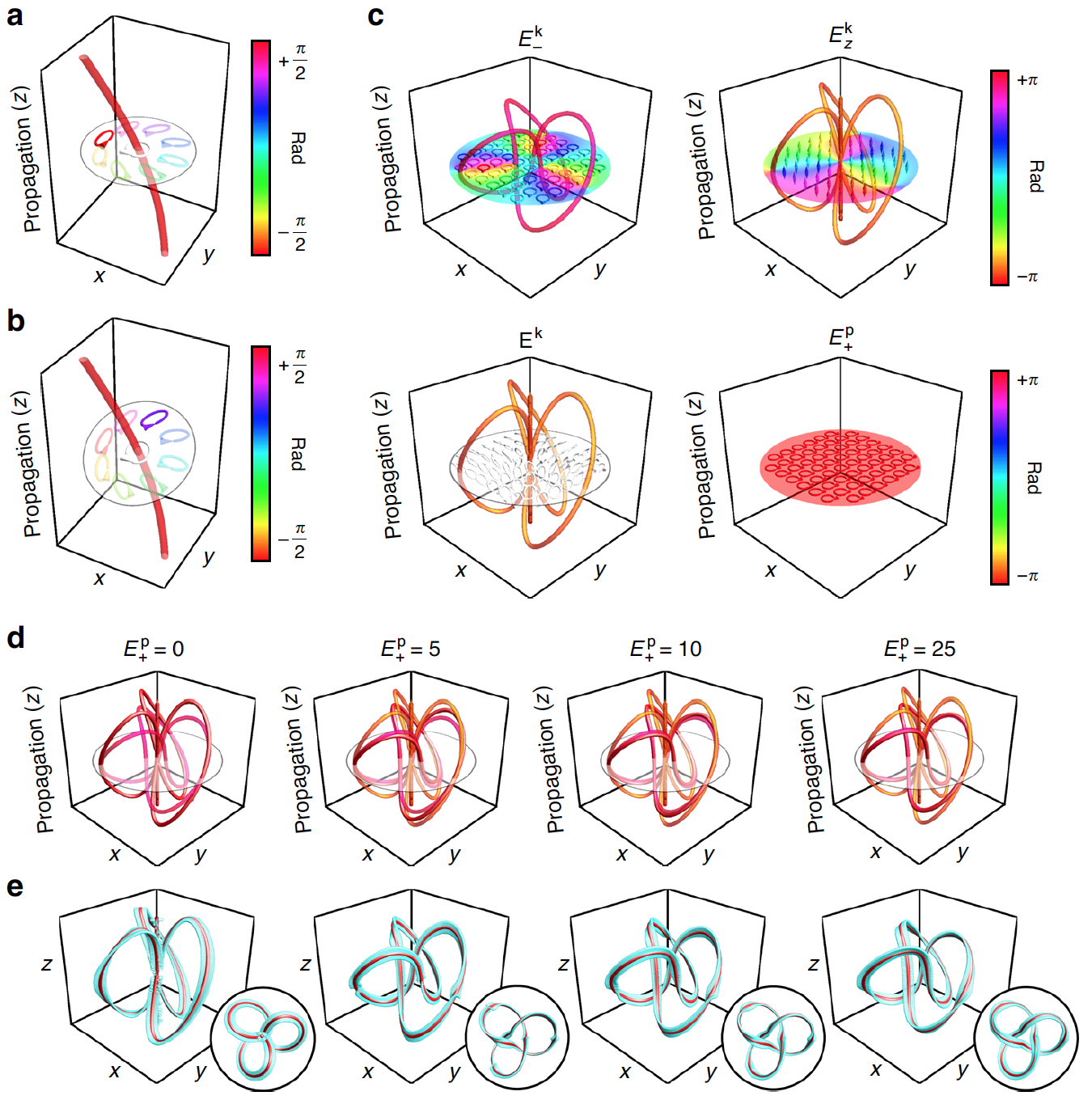
Изображение №1
В случае параксиальных* оптических лучей поляризация ограничивается плоскостью, поперечной распространению луча, например плоскостью xy.
Параксиальный луч* — луч, который распространяется вдоль оси центрированной оптической системы.
Как показано на 1а, это ограничение уменьшает плоскость, в которой можно проследить вращение оси поляризации. Однако непараксиальные лучи могут иметь векторы поляризации, нормаль которых не перпендикулярна распространению луча. Как показано на 1b, этот нормальный вектор, в свою очередь, определяет плоскость, в которой ось эллипса совершает половину оборота вокруг C-линии.
Наличие этих вращений является ключевой структурной особенностью, рассматриваемой при определении исследуемых обрамленных узлов.
Обрамленный узел в трехмерном пространстве представляет собой узел, оснащенный векторным полем, называемым обрамлением. Обрамление нигде не касается узла и характеризуется коэффициентом зацепления. Другими словами, оно считает, сколько раз векторное поле поворачивается (на 2π поворотов) вокруг узла. Узловые ленты обобщают обрамленные узлы до нечетного числа полу-скручиваний, например, узловые ленты Мебиуса.
Учитывая приведенное выше определение, обрамление замкнутой C-линии было определено осью соседнего эллипса поляризации, которого идет перпендикулярно касательной к C-линии.
Данная концепция проиллюстрирована на 1а и 1b, где разными цветами отмечены эллипсы поляризации, окружающие C-линию, ось которой перпендикулярна ее касательной, что и определяет ее обрамление.
В редком случае, когда все оси перпендикулярны в определенной точке C-линии, вектор поляризации, определяющий обрамление, можно интерпретировать как тот, который обеспечивает его непрерывность с наименьшим количеством скручиваний. Эта концепция, в свою очередь, определяет обрамление, приписываемое узловой С-линии.
На 1с показано, что это можно реализовать посредством узлового поля Ek, определяемого циркулярно поляризованной составляющей (Ek-) с узловыми фазовыми сингулярностями и продольно поляризованной составляющей (Ekz), гарантирующей, что Ek соответствует уравнениям Максвелла.
Путем наложения Ek на плоскую волну с противоположной спиральностью поляризации (Ep+) создаются узловые C-линии, возникающие из сингулярной структуры Ek (1d и 1e).
Помимо хорошо различимых трехмерных структур, узлы также могут быть представлены косами. Геометрически косы состоят из переплетенных друг с другом прядей, которые не переворачиваются на уже задействованной плоскости. Каждый узел можно представить в виде отдельной косы.
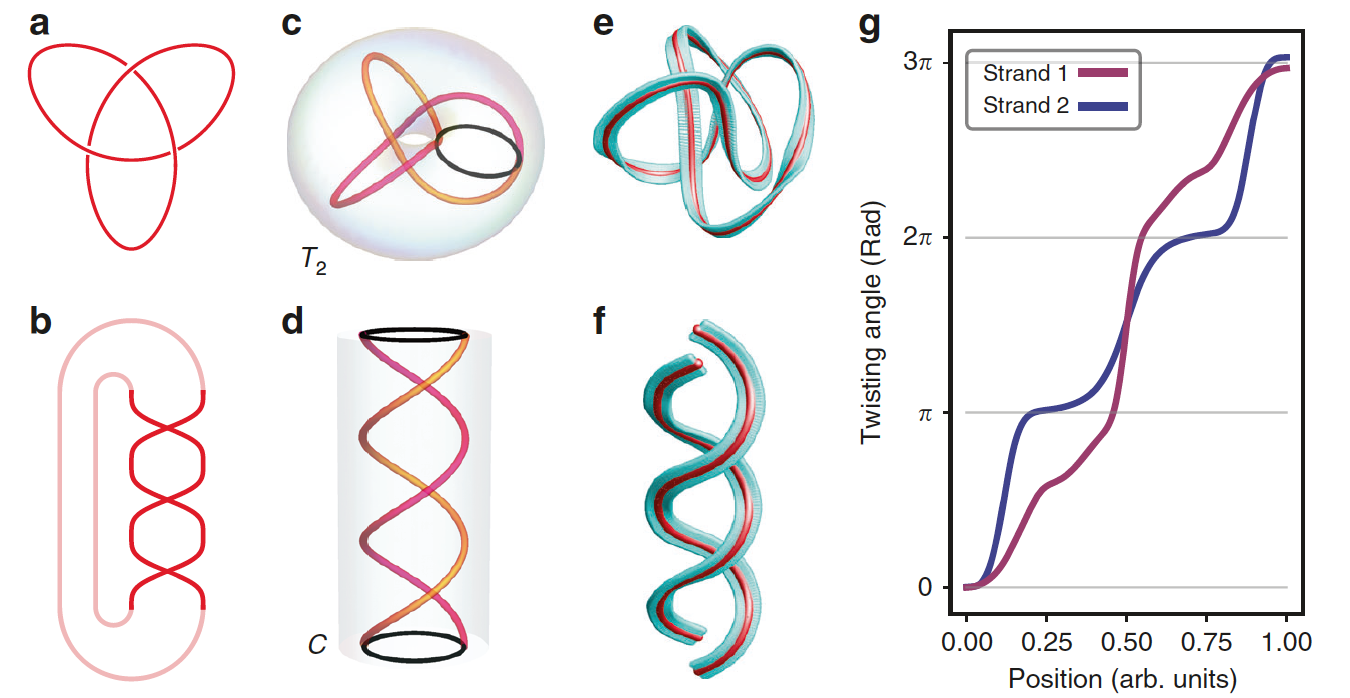
Изображение №2
Например, узел трилистник (2а) может быть выражен как закрытие косы на 2b. Такое представление можно применить и к узлам/косам в трехмерном пространстве. Например, трилистник, внедренный в тор (2c), может быть получен посредством стереографической проекции косы, заключенной в цилиндр (2d).
Один из способов выполнить эту проекцию — выразить эту косу как нули комплексного поля. Это поле записывается как функция комплексных координат (u, v), которые относятся к пространственным координатам (x, y, h), в которые коса вложена через u = x + iy и v = exp(ih). Это заплетенное поле, в свою очередь, может быть преобразовано в соответствующий ему узел со стереографической проекцией, определяемой:
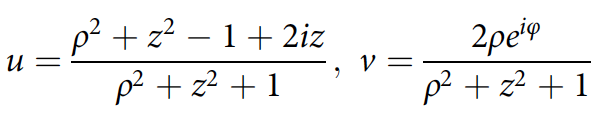
где (ρ, φ, z) — цилиндрические координаты трехмерного пространства, в которое теперь вложен узел.
Данная проекция превращает косу, определенную на (x, y, h), в узел в (ρ, φ, z), соединяя два ее конца, тем самым отображая координату h на φ.
Вышеупомянутая проекция в значительной степени используется при построении узловых оптических полей. В частности, скалярное оптическое поле может быть построено путем согласования его поля вдоль плоскости z = 0 с полем комплексного узла, возникающего в результате проекции косы. Когда это оптическое поле является параксиальным, то его формулировка в последующих z-плоскостях может быть получена с помощью методов параксиального распространения. Затем этот метод может быть расширен для описания параксиальных узловых C-линий.
Проекция, построенная из вышеуказанной формулы, была использована для создания структуры со свойствами, которые легче всего связать с оптическими узлами. Такой структурой стал тор Т2, полученный из проекции цилиндра С, охватывающий трехмерное представление соответствующей косы. Далее размеры узлов масштабировались так, чтобы их структура соответствовала Т2.
Также было использовано преобразование координат для кривой, образованной узловой С-линией. Это преобразование эффективно разрезает узел по заданному азимутальному углу и разворачивает его, тем самым сопоставляя координату φ узла с координатой h пространства. Во время этого процесса обеспечивается локальное сохранение ориентации обрамления узла. На 2е показал узел трилистник до, а на 2f этот же узел после данной процедуры.
Такое преобразование позволило определить определенную информацию касательно узлов (угол закручивания, например). В данном случае угол закручивания состоит из азимутальной ориентации ленты в обрамлении, где нормаль совпадает с касательной к развернутому узлу (2g).
Кодирование информации на узел
Учитывая возможность извлечь угол закручивания из оптического обрамленного узла, появляется возможность использовать данную структуру для записи информации.
Метод записи данных основан на паре чисел (α, β), где α — натуральное число, а β — число, связанное как с α, так и с топологической структурой обрамленного узла.
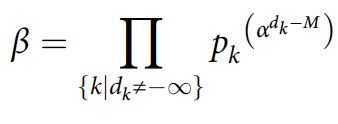
где k обозначает прядь в косе рассматриваемого обрамленного узла, dk — количество полуоборотов вдоль k пряди, демонстрирующей полуоборот (т.е. dk = −∞ если пряди не скручены), pk — простое число, присвоенное k пряди. M = Σkdk состоит из общего числа полуоборотов в обрамлении узла.
Вышеперечисленные переменные позволяют определить натуральное число:
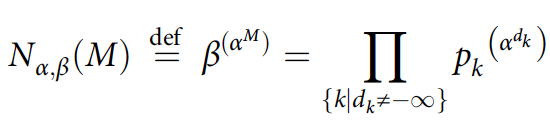
Таким образом, приведенное выше представление обрамленного узла и одной из его кос может быть использовано для кодирования и декодирования топологически защищенной информации.
Теоретический пример: Алиса и Боб
Далее ученые предлагают теоретический пример того, как этот процесс будет выглядеть. Предположим, что Алиса хотела бы отправить Бобу сообщение.
Это сообщение является результатом работы (выходные данные) программы, обрабатывающей некие входные данные (набор чисел dk, где k = 1, 2, …, n). Ожидается, что запуск программы с таким набором предоставит сообщение Алисы.
Алиса представляет свою программу и ее выходные данные в виде обрамленной косы. Сама операция, выполняемая программой, идентифицируется как последовательность пересечений на планарной диаграмме косы, а исходные данные — это количество полуоборотов на прядь. Программа Алисы полностью определена как обрамленная коса с n прядями в виде узловой ленты (КA).
Предположим, что Алиса не хочет отправлять Бобу оригинал обрамленной косы, а лишь КA. В таком случае возможно усложнить КA, тем самым скрыв (зашифровав) оригинальную обрамленную косу.
Следовательно, необходимо выполнить ряд действий. Сначала нужно выбрать натуральное число α. Далее определить проекцию обрамленной косы по отношению к КA. Для этого нужно распределить количество полуоборотов в КA для разных прядей косы, то есть установить dk так, чтобы MA = Σkdk.
Следом необходимо присвоить простые числа pk прядям, демонстрирующим полуобороты. И наконец определить число β согласно формуле №2.
После того как данная процедура завершена, Алиса может отправить Бобу ленту КA, завязанную узлом, и числа (α, β).
Естественно, полученное сообщение необходимо расшифровать. Для этого Боб должен вычислить Nα, β(MA), разложение которых на простые множители дает dk. За счет этого Боб может восстановить оригинал обрамленной косы, которую отправила ему Алиса.
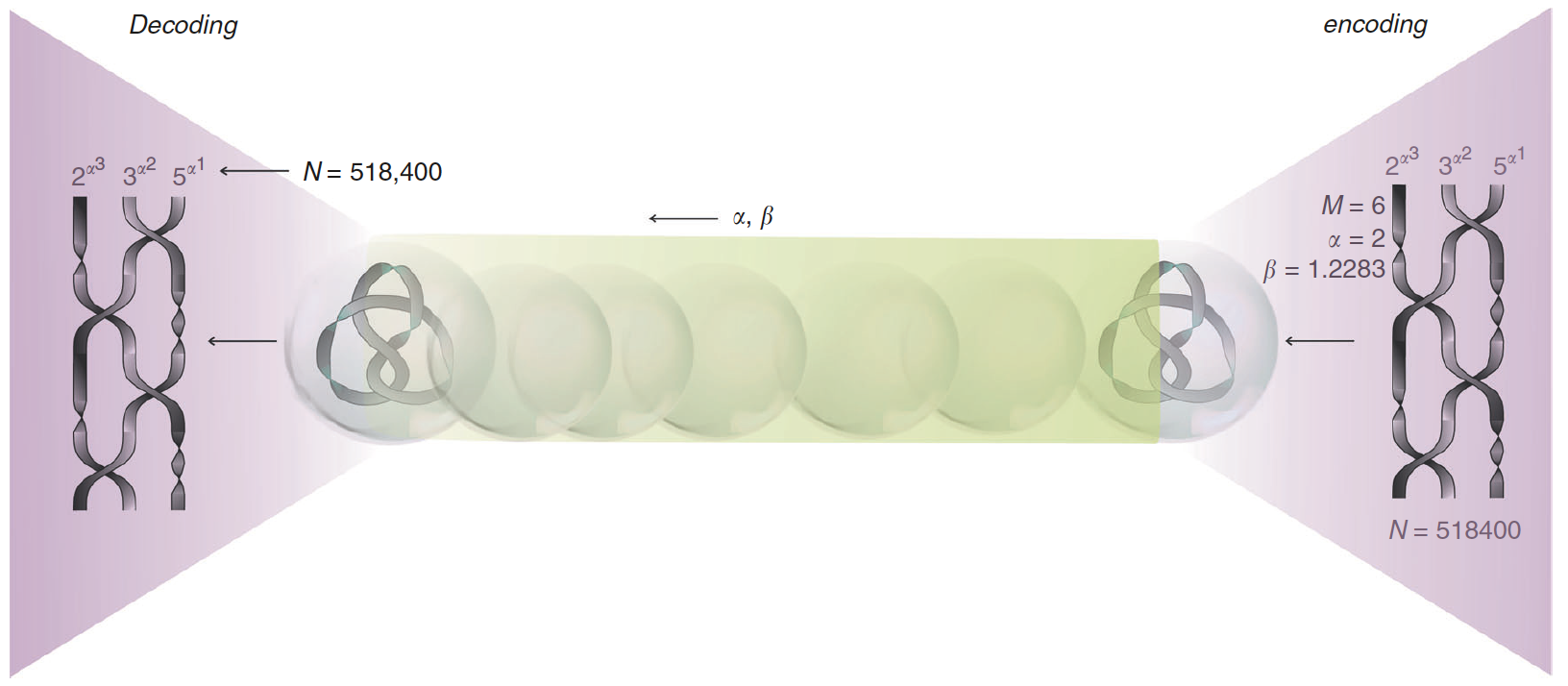
Изображение №3
Данная операция по обмену данными показана на схеме выше.
Если свести все к простым терминам, то у Алисы есть лента (данные), которая она хочет передать Бобу. Эту ленту можно преобразовать в сложный узел и закодировать исходное состояние, предоставив средства для декодирования исключительно Бобу.
Практические эксперименты
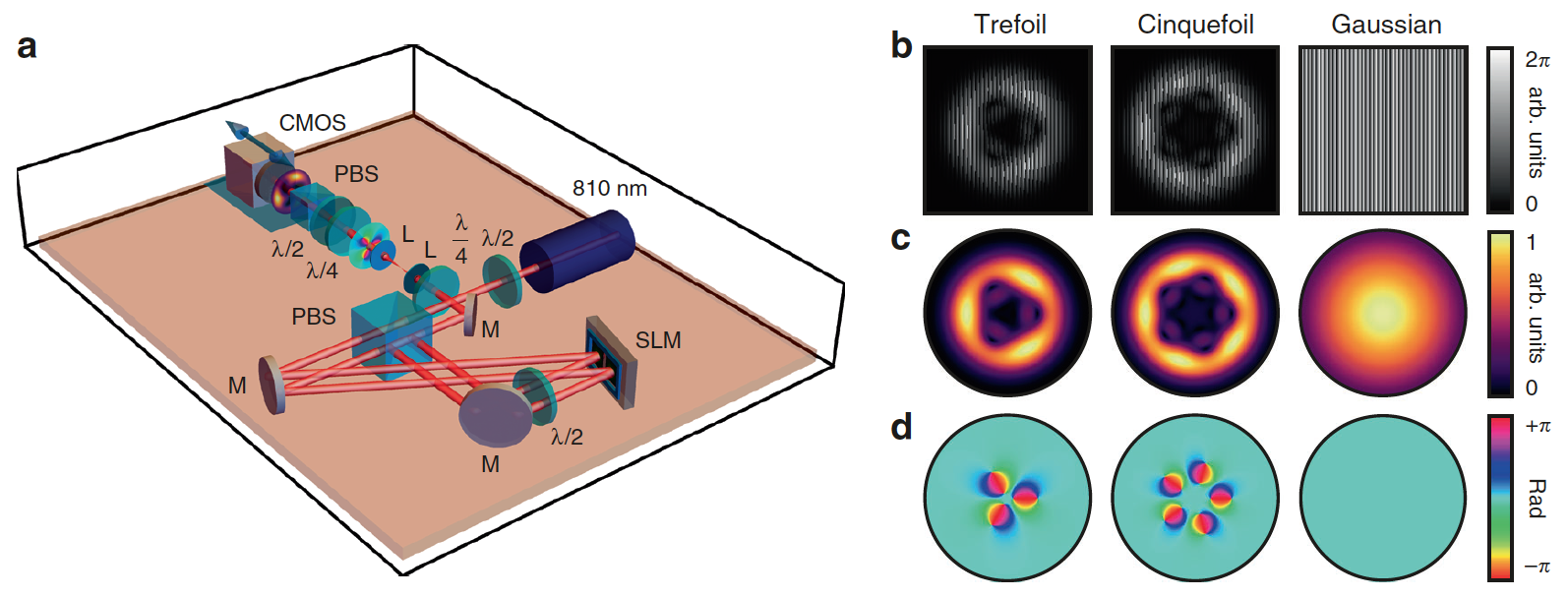
Изображение №4
Следующим этапом исследования стала практическая реализация приведенного выше теоретического примера. В опыте были использованы параксиально-узловые C-линии, полученные посредством интерферометра Саньяка (4а).
Это устройство разделяет однородно поляризованный световой луч на две ортогонально поляризованные компоненты, каждая из которых модулируется пространственным модулятором света (SLM от spatial light modulator). SLM отображает голограммы, в которых зашифрованы как интенсивность, так и фаза целевого оптического поля.
Одна компонента модулируется для получения пучка с узловыми оптическими вихрями, такими как Ek- (1c). Вторая компонента модулируется, чтобы сформировать большой гауссов пучок, который равномерно покрывает всю узловую составляющую, тем самым эффективно принимая на себя роль плоской волны Ep+ (1c).
На выходе из интерферометра два луча когерентно складываются, тем самым преобразуя узловые фазовые вихри Ek- в параксиально-узловые C-линии. Узел и его обрамление затем можно реконструировать с помощью измерений поляризационной томографии, позволяющих получить профиль поляризации поля.
С помощью данной экспериментальной установки удается получить узлы разных типов: трилистник и печать Соломона (пятилистник). На 4b показаны голограммы, отображаемые на SLM, а также амплитуды и фазы полей, которые они должны создавать.
Фаза поля для узла трилистника и для узла пятилистника представлены следующими формулами:
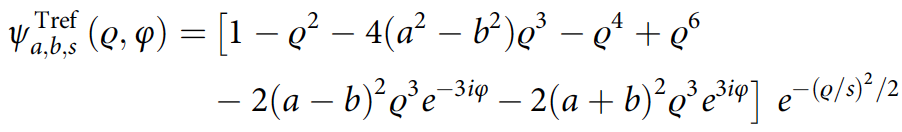
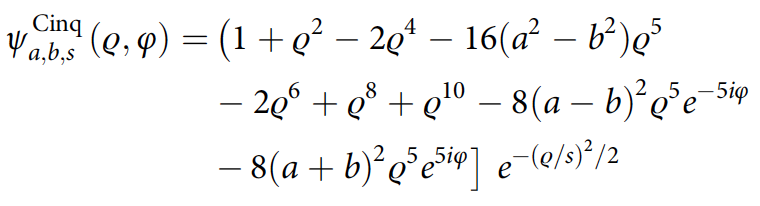
где ϱ — масштабированная и безразмерная версия цилиндрической радиальной координаты, φ — азимутальная координата, a, b, s — параметры, определяющие форму узла.
Для узла-трилистника рассматривались параметры a = 1, b = 0.5 и s = 1,2, тогда как для узла-пятилистника использовались a = 0.5, b = 0.24 и s = 0.65.

Изображение №5
Обрамленные узлы, полученные в ходе теоретических опытов, показаны на 5а. А вот на 5b показаны узлы, полученные в ходе практических опытов. Помимо незначительных дефектов, возникающих в местах стыковки С-линий на концах узлов, наблюдается очень хорошее согласование теории и экспериментальных результатов. Схемы 5с показывают развернутый вариант экспериментально полученных узлов. Сравнение числа полуоборотов также показало значительное совпадение теории и практики (5d).
Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.
Эпилог
Если очень и очень грубо суммировать колоссальный труд ученых, то мы получим две вещи. Во-первых, из лучей света можно вязать узлы разной степени сложности. Во-вторых, этот процесс позволяет записывать информацию, которая будет закодирована в ходе образования узлов.
Как отмечают сами ученые, ранее подобные структуры (оптические узлы) уже изучались, однако лишь как двумерные системы. В этом же труде их наконец-то рассмотрели как полноценные трехмерные структуры, что позволило куда лучше понять их свойства и возможные варианты применения.
Одним из таких применений является передача зашифрованных данных. Авторы исследования заявляют, что современные технологии позволяют с высокой точностью манипулировать различными параметрами лучей света (интенсивность, фаза, длина волны и т.д.). Возможность менять эти параметры позволяет кодировать и декодировать информацию посредством исключительно оптических методов.
Кроме того, данное исследование может помочь в топологических квантовых вычислениях, поскольку можно существенно снизить степень шума, который является одной из основных проблем в данной области. Конечно, это лишь теоретические предположения, которые еще предстоит проверить на практике. Тем не менее результатов, полученных в ходе данного исследования, уже достаточно, чтобы более оптимистично смотреть на грандиозные планы ученых.
Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята. :)
Немного рекламы
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5–2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле в дата-центре Equinix Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5–2697v3 2.6GHz 14C 64GB DDR4 4×960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5–2430 2.2Ghz 6C 128GB DDR3 2×960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5–2650 v4 стоимостью 9000 евро за копейки?
