Магия тензорной алгебры: Часть 15 — Движение несвободного твердого тела
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
В прошлый раз мы рассмотрели один из способов получения дифференциальных уравнений движения твердого тела исходя из принципа Даламбера. Мы остановились на общей форме уравнений движения
Однако, внимательно взглянув на эти уравнения, меня следовало бы раскритиковать — дело в том, что в данных уравнениях число неизвестных слишком велико. К неизвестным следует отнести ускорение полюса и угловое ускорение тела
, а также реакции связей
. И если движение тела ограничено хотя бы одной связью, число неизвестных величин в (1) и (2) превышает число уравнений.
Это происходит потому, что левая часть уравнений (1) и (2) содержит ускорения, вычисляемые для случая свободного движения тела, то есть в них имеются избыточные координаты. Поэтому, систему (1), (2) следует дополнить уравнениями связей, описывающими ограничения, налагаемые связями на координаты, скорости и ускорения точек тела.
Этим мы сейчас и займемся — посмотрим, во что превращаются уравнения (1) и (2) при добавлении уравнений связей, и что дают нам полученные уравнения в практическом смысле.
Свободным называют такое тело, движение которого не ограничено связями. Соответственно в уравнениях (1) и (2) пропадают лишние неизвестные и они превращаются в
И для свободного тела нет смысла использовать произвольный полюс — лучше сменить центр приведения систем сил инерции на центр масс тела, записав уравнения движения в более простой форме
Уравнения (5) и (6) — дифференциальные уравнения свободного движения твердого тела. Они могут быть разрешены относительно ускорений и проинтегрированы численно, при заданных начальных условиях.
А теперь предположим, что движение тела ограничено сферическим шарниром, расположенным в точке . Тогда, выбрав полюс в этой неподвижной точке, мы можем добавить уравнение связи
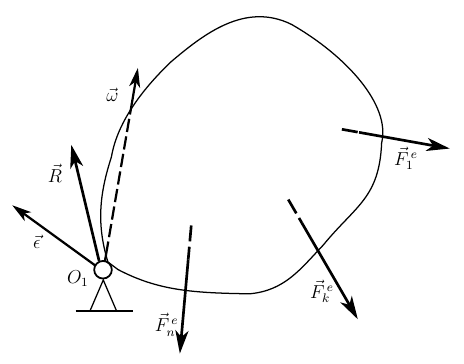
Реакция сферического шарнира, выражается одной силой , поэтому, с учетом (7) уравнения (1) и (2) можно переписать в виде
причем , так как сила
приложена в точке
, значит, получаем окончательно
Уравнение (8) позволяет определить угловое ускорение тела, исходя из начальных условий задачи и известных активных сил, приложенных к телу, а уравнение (9) дает возможность, зная угловое ускорение, найти реакцию сферического шарнира. Таким образом мы получаем дифференциальные уравнения сферического движения.
Вращательным называется движение тела, когда две его точки остаются неподвижными в любой момент времени. Если выразить этот факт с помощью уравнений, то мы можем записать следующие уравнения связей
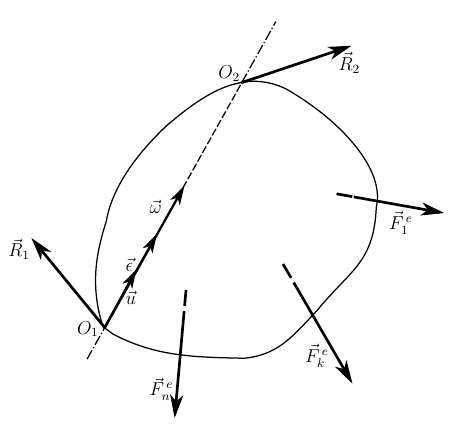
Условие (10) выражает неподвижность одной из точек тела, а условие (11) — неизменность направления оси вращения тела. Исходя из (11) можно выписать угловую скорость и угловое ускорение тела через параметры конечного поворота
Подставляем (12) и (10) в уравнение (2)
учитывая, что у нас две связи, и соответственно две реакции от подшипников, на которых происходит поворот тела. Причем сразу можно учесть, что , так как первая реакция приложена в точке
. Кроме того выполним скалярное умножение последнего уравнения на орт оси вращения
Учтем, что момент второй реакции можно вычислить как , при этом
, то есть получаем
Вторые слагаемые в обеих частях данного уравнения — смешанные произведения компланарных векторов и равны нулю, в итоге имеем
— дифференциальное уравнение вращения тела вокруг неподвижной оси, где
называют моментом инерции твердого тела относительно оси вращения, а
— проекция векторного момента относительно неподвижной точки на ось проходящую через эту точку или — момент силы относительно оси.
Выражение (14) крайне интересно. Если переписать его в тензорной форме, то мы получим формулу
позволяющую, по известному тензору инерции твердого тела определить его момент инерции относительно интересующей нас оси вращения, направление которой в пространстве задано ортом . Момент инерции (16) является скалярной величиной, характеризующей распределение массы тела вокруг оси вращения. Эта величина, равно как и уравнение (13) хорошо известны из общего курса теоретической механики.
При поступательном движении, связи, наложенные на тело препятствуют его вращению. В этом случае мы можем записать очевидные равенства
Полагая идеальность связей, мы можем записать условие, накладываемое на их реакции
где — вектор, касательный к траекториям точек тела. В случае поступательного движения, траектории всех его точек одинаковы, а значит и вектор касательной к траектории одинаков для всех точек. С учетом (17) и (18) можно переписать уравнение (1)
или
— дифференциальное уравнение поступательного движения тела в проекциях на касательную к траекториям его точек.
В данной статье мы рассмотрели, как преобразуются общие уравнения движения твердого тела (1) и (2) если дополнить их уравнениями связей. При этом, мы легко и непринужденно построили дифференциальные уравнения движения для всех частных случаев движения тела, изучаемых теоретической механикой.
при подготовке данной статьи использован метод, предложенный пользователем SeptiM. В связи с очевидным удобством работы, хочу выразить признательность автору, за проделанную им работу.
Продолжение следует…
