Логика сознания. Часть 9. Искусственные нейронные сети и миниколонки реальной коры
Приходит ветеринар к терапевту. Терапевт: — На что жалуетесь? Ветеринар: — Нет, ну так каждый может!
Искусственные нейронные сети способны обучаться. Воспринимая множество примеров, они могут самостоятельно находить в данных закономерности и выделять скрытые в них признаки. Искусственные нейронные сети во многих задачах показывают очень неплохие результаты. Закономерный вопрос — насколько нейронные сети похожи на реальный мозг? Ответ на этот вопрос важен главным образом для того, чтобы понять, можно ли, развивая идеологию искусственных нейронных сетей, добиться того же, на что способен человеческий мозг? Важно понять, носят ли различия косметический или идеологический характер.
Как это ни удивительно, но очень похоже, что реальный мозг противоречит всем базовым принципам искусственных нейронных сетей. Это вдвойне удивительно, учитывая, что изначально искусственные нейронные сети создавались как попытка воспроизвести именно биологические механизмы. Но в том и коварство подобных ситуаций. Очень часто то, что на первый взгляд выглядит правдоподобно, на поверку оказывается полной противоположностью того, что есть на самом деле.
Искусственные нейронные сети
Перед тем как описать механизмы обучения реальных нейронов перечислим основные принципы, на которых основываются искусственные нейронные сети. Этих принципов несколько. Все они очень тесно связаны между собой. Нарушение любого из них ломает всю концепцию работы искусственных нейронных сетей. После этого мы покажем, что в «настоящих нейронных сетях» не выполняется ни один из этих принципов.
Принцип 1. Каждый нейрон — это детектор некого свойства.
Реальный нейрон, если описывать его упрощенно, выглядит достаточно просто. На дендритах располагаются синапсы. Синапсы контактируют с другими нейронами. Сигналы от других нейронов через синапсы поступают в тело нейрона, где суммируются. Если сумма превышает определенный порог, то возникает собственный сигнал нейрона — спайк, он же потенциал действия. Спайк распространяется по аксону и поступает на другие нейроны. Синапсы могут менять свою чувствительность. Таким образом нейрон может настраиваться реагировать на определенные комбинации активности других нейронов.
Все это хотя и выглядит достаточно правдоподобно очень далеко от работы реальных нейронов. Но пока мы описываем классическую модель и будем следовать такой логике.

Упрощенная схема реального нейрона
Из описанного выше с неизбежностью следует формальная модель — искусственный нейрон Маккалока — Питтса, разработанный в начале 1940-х годов (Маккалох Дж., Питтс У., 1956).

Формальный нейрон Маккалока — Питтса
На входы такого нейрона подаются сигналы. Эти сигналы взвешенно суммируются. Далее к этой линейной комбинации применяется некая нелинейная функция активации, например, сигмоидальная. Часто как сигмоидальную используют логистическую функцию: 

Логистическая функция
В этом случае активность формального нейрона записывается как
В итоге такой нейрон превращается в пороговый сумматор. При достаточно крутой пороговой функции сигнал выхода нейрона — либо 0, либо 1. Взвешенная сумма входного сигнала и весов нейрона — это сравнение двух образов: образа входного сигнала и образа, описываемого весами нейрона. Результат сравнения тем выше, чем точнее соответствие этих образов. То есть нейрон, по сути, определяет, насколько подаваемый сигнал похож на образ, записанный на его синапсах. Когда значение взвешенной суммы превышает определенный уровень, и пороговая функция переключается в единицу, это можно интерпретировать как решительное заявление нейрона о том, что он узнал предъявляемый образ.
В разных моделях возможны различные вариации того, как должен срабатывать искусственный нейрон. Если убрать пороговую функцию, то нейрон превратится в линейный сумматор. Можно вместо сравнения с шаблоном, который задает веса, проверять входной сигнал на соответствие многомерному нормальному распределению с определенными параметрами, это используется в сетях на основе радиально-базисных функций. Можно подавать сигналы, распределенные во времени, и вводить для синапсов временные параметры, настраивая таким образом нейрон на чувствительность к определенным последовательностям. Возможны и другие варианты. Общее между всеми ними — это соответствие нейрона знаменитой концепции «нейрона-бабушки».
Ключевой момент для всех нейронных сетей — это восприятие нейронов, как детекторов каких-либо свойств. Нечто появляется в описании — нейрон, который соответствует этому «нечто» реагирует на это своей активностью. Вариации нейронных сетей — это вариации методов детектирования и обучения этому детектированию.
Принцип 2. Информация в нейронной сети — это признаковое описание.
В классическом представлении каждый нейрон видит картину активности других нейронов, которые создают его входной сигнал. При этом каждый нейрон является детектором чего-то. Если собрать входной сигнал в вектор, то получится так называемое признаковое описание.
В признаковом описании, как следует из названия, каждый элемент вектора описания соответствует определенному признаку. При этом не принципиально, как задан элемент. Это может быть бинарное значение — присутствует признак или нет. Может быть количественное значение — насколько выражен признак в описании. Порядковое или номинальное значение — как реализовался в описании этот признак.
Например, возьмем бинарный 32-битный вектор. Будем кодировать буквы английского алфавита.
Первый вариант. Нулевой бит — буква «A», первый бит буква «B» и так далее. 26 бит будут советовать 26 буквам. Затем сделаем бит — заглавная буква или прописная. Бит — курсив или не курсив, бит на толщину, бит на подчеркивание и так далее. Если зараз кодировать одну букву, то можно закодировать одну из 26 букв в разных вариантах написания. Это типичное признаковое описание. Каждый бит — это определенный признак.
Второй вариант. Машинная кодировка, типа, юникод. Символы кодируются уникальными бинарными кодами. Но отдельные биты уже не являются признаками. В кодах разных несвязанных между собой букв могут быть общие единицы. Такое кодирование уже не является признаковым описанием, хотя внешне и там, и там 32 битный бинарный вектор.
Информация, с которой имеют дело нейронные сети — это всегда признаковое описание. И это следует из первого принципа, согласно которому нейроны — детекторы признаков.
Принцип 3. Нейронная сеть, как правило, — это преобразователь признаковых описаний.
Вход нейронной сети — это признаковое описание. Результат работы — также признаковое описание, но состоящее уже из других признаков. Например, если мы хотим сделать сеть, которая будет узнавать цифры по их изображению, то входными признаками могут быть значения яркости точек картинки, а выходными распознанные цифры.
Преобразуя одно признаковое описание в другое, может оказаться полезным использовать промежуточные признаки, которых нет ни во входном, ни в выходном описании. Можно сделать несколько слоев таких промежуточных признаков. Такие нейронные сети выглядят наподобие того, что показано на рисунке ниже.

Многослойный персептрон с двумя скрытыми слоями (Хайкин, 2006)
Типичный пример нейронной сети со скрытыми признаками — это слоистая сеть прямого распространения. Каждый слой такой сети, кроме входного, состоит из нейронов-детекторов. Эти нейроны настраиваются на узнавание определенных признаков. Каждый слой повторяет исходное описание, но уже в своих, характерных для этого слоя признаках.
Если выход сети снова подать на вход, то получится динамическая рекуррентная сеть. В сети прямого распространения состояние выхода определяется сразу после активации всех нейронов. В рекуррентной сети только со временем возникает устойчивое состояние, которое и является результатом ее работы.
Независимо от типа сети на каждом слое мы имеем дело с признаковым описанием, составленным из нейронов-детекторов.
Принцип 4. Количество нейронов в сети определяет число признаков, с которыми может работать эта сеть.
Количество нейронов на каком-либо слое сети определяет то, сколько максимально признаков доступно для выделения этому слою. Обычно количество нейронов в сети задается изначально перед началом обучения. Так как заранее неизвестно, сколько полезных признаков может выделиться, то оптимальное число нейронов в слоях подбирают итерационно.
В принципе, можно при необходимости «на лету» добавлять новые нейроны, но это требует особого подхода к обучению и связано с существенными сложностями.
Принцип 5. Обучение сети — это настройка весов соединяющих нейроны связей.
Детектором какого свойства является тот или иной искусственный нейрон определяется тем, какие значения принимают его веса. Обучение нейронной сети происходит за счет такого изменения весов нейронов, которое оптимизирует те требования, что мы к этой сети предъявляем.
Два основных вида обучения — это обучение без учителя и обучение с учителем.
Обучение без учителя
При обучении без учителя нейронная сеть наблюдает за входными данными, не имея заранее представления о том, какой выходной сигнал должен соответствовать тем или иным событиям. Но так как в данных могут содержаться определенные закономерности, то можно так настроить поведение сети, чтобы ее нейроны стали реагировать каждый на свою закономерность.
Например, можно взять однослойную сеть, состоящую из линейных сумматоров, и заставить ее выделять главные компоненты подаваемого набора данных. Для этого можно инициировать сеть случайными весами, при подаче сигнала определять победителя и затем сдвигать его веса в сторону поданного сигнала. В итоге нейроны сами «растащат» между собой основные факторы, содержащиеся во входной информации.
Можно сделать автокодировщик. Создать сеть из трех слоев с условием, что средний слой должен быть меньше по размеру чем входной слой, а выходной слой должен быть равен входному. Задача автокодировщика — как можно точнее воспроизводить на выходном слое картину входного слоя.

Автокодировщик
Так как по дороге от входа к выходу стоит слой с меньшей размерностью, то автокодировщику придется научиться сжимать данные, то есть выделять на нейронах среднего слоя наиболее значимые факторы. Средний слой в последствии и будет являться рабочим выходом сети.
Для обучения автокодировщика можно на каждом шаге считать ошибку между первым и третьим слоем и корректировать веса сети в сторону уменьшения этой ошибки. Это позволяет сделать, например, метод обратного распространения ошибки.
Могут быть и другие методы. Например, сеть радиальных базисных функций, основываясь на идеях EM алгоритма, может осуществлять решение задачи классификации. В такой сети нейроны скрытого слоя оценивают не соответствие подаваемого образа и образа, задаваемого весами нейрона, а вероятность соответствия входного сигнала нормальным распределениям, параметры которых хранятся в этих нейронах.
Обучение с учителем
При обучении с учителем мы заранее определяем какой выходной сигнал мы хотим получить от сети в каждом из обучающих примеров. Задача обучения — это так настроить веса, чтобы сеть наиболее точно угадывала ответы из обучающего набора. Тогда появляется надежда, что сеть уловила закономерности и сможет угадывать выходной сигнал и для данных, которых не было при обучении.
Для сети прямого распространения обучение выглядит следующим образом. Изначально сеть инициируется случайными весами. Подается обучающий пример и вычисляется активность сети. Формируется представление об ошибке, то есть разность между тем, что должно быть на выходном слое и что получилось у сети. Далее веса корректируются так, чтобы уменьшить эту ошибку.
Для однослойного персептрона можно воспользоваться дельта-правилом.
Дельта-правило очень похоже на правило Хебба, которое имеет очень простой смысл: связи нейронов, активирующихся совместно, должны усиливаться, а связи нейронов, срабатывающих независимо, должны ослабевать. Но правило Хебба изначально сформулировано для обучения без учителя и позволяет нейронам самим настраиваться на выделение факторов. При обучении с учителем совместную активность надо понимать несколько иначе. В этом случае правило Хебба приобретает вид:
- Первое правило — Если выходной сигнал персептрона неверен и равен нулю, то необходимо увеличить веса тех входов, на которые была подана единица.
- Второе правило — Если выходной сигнал персептрона неверен и равен единице, то необходимо уменьшить веса тех входов, на которые была подана единица.
Если Y — это вектор реального выхода персептрона, а D — вектор, который мы ожидаем получить, то вектор ошибки:

Дельта-правило для изменения связи между i и j нейронами:

По сути в однослойной сети мы пытаемся построить на нейронах выходного слоя портреты выходных признаков в терминах входных признаков. Весами связей мы задаем наиболее характерный, типовой портрет выходного признака.
Сложности начинаются, когда оказывается, что однозначного портрета может не существовать. Например, когда мы пытаемся узнавать буквы, то при обучении мы можем использовать и прописные и заглавные буквы. При это если мы не делаем между ними разницы, то выходной нейрон, отвечающий за букву «А» должен будет реагировать сразу на два образа — образ «А» и образ «а». Аналогично, написание букв может быть совершенно различным в разных почерках. Если пытаться совместить все эти портреты на одном нейроне, то ничего хорошего не получится. Образ будет столь размыт, что может оказаться практически бесполезен.
В таких случаях помогает многослойная сеть со скрытыми слоями. На нейронах скрытых слоев могут формироваться самостоятельные портреты различных реализаций выходных признаков. Кроме того, в скрытых слоях могут выделяться факторы, общие для разных выходных нейронов и при этом полезные для дифференциации одних выходных признаков от других.
Для обучения многослойной сети используется метод обратного распространения ошибки. Метод состоит из двух проходов: прямого и обратного. При прямом проходе подается обучающий сигнал и рассчитывается активность всех узлов сети, включая активность выходного слоя. Вычитанием полученной активности из того, что требовалось получить, определяется сигнал ошибки. При обратном проходе сигнал ошибки распространяется в обратном направлении, от выхода ко входу. При этом синаптические веса настраиваются с целью минимизации этой ошибки.
Принцип 6. Конечность обучения. Дилемма стабильности-пластичности.
При обучении нейронной сети каждый раз после подачи нового обучающего примера вычисляется некая поправка к весам связей. При этом вычисляются градиенты, которые указывают, в какую сторону стоит ту или иную связь изменить, усилить или ослабить.
В начале обучения можно вести себя достаточно смело и относительно сильно корректировать связи нейронов. Но по мере обучения оказывается, что резкие изменения уже недопустимы, так как они начинают переучивать сеть, подстраивая ее под новый опыт, затирая при этом опыт предыдущий. Выход достаточно очевиден. В алгоритмы вводится параметр скорости обучения. По мере обучения скорость уменьшается и новый опыт уже не радикально меняет веса, а только слегка их подправляет.
Недостаток такого подхода в том, что с определенного момента сеть «костенеет» и перестает изменяться. По этой причине традиционные сети трудно дообучать. Если появляется такая необходимость, то оказывается проще заново с нуля обучить сеть на расширенном наборе данных, включающем как старый так и новый опыт.
Вопрос дообучения упирается в то, что новый опыт начинает менять веса сети и тем самым изменяет старое обучение. Проблема разрушения старого опыта новой информацией называется дилеммой стабильности-пластичности.
Вариант решения предложен Стефаном Гроссбергом (Grossberg, 1987) как «теория адаптивного резонанса». Суть этой теории в том, что поступающая информация делится на классы. Каждый класс имеет свой прототип — образ, наиболее точно соответствующий этому классу. Для новой информации определяется, принадлежит ли она к одному из существующих классов, либо она является уникальной, непохожей ни на что предыдущее. Если информация не уникальна, то она используется для уточнения прототипа класса. Если же это что-то принципиально новое, то создается новый класс, прототипом которого ложится этот образ. Такой подход позволяет, с одной стороны, создавать новые детекторы, а с другой стороны, не разрушать уже созданные.
Но идеология адаптивного резонанса плохо совместима с остальными методами обучения, так как, по сути, требует добавления новых нейронов прямо в процессе обучения сети.
Модель обучения с активной памятью
Различают два подхода к обучению — адаптивный и пакетный. При адаптивном обучении новый опыт используется для некоторого изменения ранее достигнутого состояния весов сети с целью адаптировать их к этому новому опыту. При этом полагается, что веса сети уже учитывают в себе все, что связано с ранее полученным опытом. В пакетном подходе исходят из того, что при получении нового примера нам остается доступен весь предыдущий опыт и при обучении мы можем не адаптировать веса, а просто рассчитать их заново.
Хранение предыдущего опыта сильно упрощает вопрос стабильности-пластичности сети.
Рассмотрим задачу распознавание цифр, например, набора MNIST. На вход нейронной сети подаются изображения рукописных цифр, на выходе смотрят за реакцией нейронов, соответствующих цифрам от 0 до 9. Входные изображения имеют размер 28 на 28 пикселей, всего 784 точки.

Пример рукописных цифр набора MNIST
Обычно для решения такого рода задач используют сверточные сети и многоуровневую архитектуру. Подробнее работу таких сетей мы рассмотрим позже. В силу простоты и предварительной подготовленности набора MNIST (все цифры одного размера и отцентрованы) хорошие результаты получаются даже при применении простого однослойного или двуслойного персептрона.
На рисунке ниже приведена самая простая однослойная сеть. Вход этой сети — 784 точки изображения. Выход — нейроны, соответствующие цифрам.

Однослойная сеть для распознавания рукописных цифр
Обучать такую сеть можно, например, дельта-правилом. В результате обучения веса выходных нейронов настроятся на некие усреднено-схематичные образы цифр. Размытые настолько, чтобы максимально «покрывать» свои прототипы, но при этом не сильно «наползать» на другие цифры. Параметр скорости обучения здесь имеет вполне конкретную трактовку. Так как происходит своеобразное усреднение изображений одной цифры, то вклад каждого следующего примера в формирование усреднения должен быть обратно пропорционален количеству уже прошедших примеров.
В обучающем наборе одни и те же цифры есть в разном написании. Например, двойка «просто» и двойка с «петелькой» в основании (рисунок ниже). Простой сети ничего не остается кроме как построить гибридный портрет, что, конечно, не улучшает качества ее работы.

Варианты «двойки»
В многослойной сети появляется надежда, что в скрытых слоях варианты основания двойки выделяться отдельными признаками. Тогда выходной слой сможет увереннее узнавать двойку, ориентируясь на появление одного из этих признаков.
Создание усредненных размытых портретов позволяет успешно узнавать образы в большинстве случаев, но накладывает предел на достижимое качество узнавания. Размытие неизбежно ведет к потере информации.
При обучении нейронов выходного слоя создаются «хорошие» классификаторы для каждой из цифр. Их веса — это лучшее, что можно получить из идеологии «давайте сделаем портрет класса».
Когда компьютеры были слабыми или, вообще не дай бог, приходилось считать вручную, очень важно было использовать такие методы, которые позволяли бы минимальными вычислениями получать хорошие результаты. Многие идеи «хороших» алгоритмов исходят именно из такой экономии вычислений. Надо сделать некую дискриминантную функцию, которая позволит вычислить принадлежность объекта к классу. Или надо вычислить главные факторы и оперировать описанием в них вместо исходных данных.
Для любого «хорошего» базового алгоритма существует предел достижимой точности, который определяется тем, какой процент информации был им потерян в процессе построения факторов или создания дискриминантной функции.
Улучшить общий результат можно за счет применения сразу нескольких различных классификаторов. Из нескольких классификаторов можно создать комитет, который голосованием будет принимать решения об отнесении объекта к классу. Такой подход называется бустингом.
При бустинге не обязательно использовать «хорошие» классификаторы. Годятся любые неслучайные, то есть такие у которых вероятность правильного отнесения выше вероятности случайного выбора. Самое интересное, что во многих случаях, увеличивая количество «плохих», но неслучайных классификаторов, можно добиться сколь угодно точного результата. Справедливы такие рассуждения и для искусственных нейронных сетей.
Идеология нейронов-детекторов, обученных на размыто-усредненный образ, — это во многом дань «экономным» методам вычислений. Правда, само обучение далеко не всегда можно назвать экономным и быстрым, но зато результат — это сеть с относительно небольшим количеством нейронов.
Альтернативой концепции «хороших» нейронов-детекторов может выступать концепция «активной памяти». Каждый отдельный обучающий пример — это образ, который может самостоятельно выступать классификатором. То есть, на каждый обучающий пример можно создавать отдельный нейрон, веса которого будут копировать входной сигнал. Такой нейрон может работать, например, в режиме линейного сумматора, тогда его реакция будет тем сильнее, чем больше будет похож подаваемый сигнал на запомненный им образ. Из таких воспоминаний детекторов можно собрать сеть, показанную на рисунке ниже.

Нейронная сеть с воспоминаниями-детекторами. Связи воспоминаний и выходных нейронов несколько сложнее, чем просто суммирование
В приведенной на рисунке сети входной слой нейронов передает свой сигнал на элементы второго среднего слоя. Элементы второго слоя не будем называть нейронами, а назовем воспоминаниями. Каждый обучающий пример создает новое воспоминание. При подаче примера вновь созданное воспоминание отпечатывает на себе точный образ сигнала входного слоя. Выход элемента-воспоминания замыкается на нейроне выходного слоя, соответствующем тому, что предписывает правильный ответ.
Обучение такой сети с учителем сводится к запоминанию примеров и созданию связей типа «пример-ответ».
В режиме распознавания каждое воспоминание самостоятельно определяет степень своей похожести на текущий образ. Из совокупного срабатывания воспоминаний создается информация для выходного слоя, которая позволяет понять, какому нейрону стоит активироваться.
При внешней простоте сети с памятью ее работа не так проста, как может показаться. От элементов этой сети требуется значительно более сложная логика работы, чем от традиционных формальных нейронов.
Механизм сравнения
Механизм сравнения воспоминания и образа зависит от формы представления описания. Надо сказать, что признаковое описание — достаточно неудачная форма. Например, две соседние по картинке точки в признаковом описании дают нулевое совпадение, если для сравнения используется скалярное произведение соответствующих описаниям векторов. Именно по этой причине при кодировании картинки через вектор, описывающий яркость отдельных точек, «размытое» описание оказывается предпочтительнее «четкого». В размытых картинках вместо отдельной точки появляется «пятно». Соответственно, близкие точки начинают давать определенное совпадение при сравнении (рисунок ниже).

Единичное смещение приводит к полному отсутствию совпадения (слева). Аналогичная ситуация после размытия дает существенное совпадения (справа) (Fukushima K., 2013)
Идея с «размытием» подходит не только для изображений, но и для любых признаковых описаний. Для этого требуется задать матрицу близости признаков описания. Тогда для любого входного сигнала перед сравнением можно создавать его «размытие» и уже его использовать в скалярном произведении. Для картинок близость признаков определяется близостью точек на изображении. Для произвольных сигналов задать близость признаков несколько сложнее. Иногда в этом может помочь статистика их совместного проявления.
Если «размывание» используется для сравнения одного «четкого» сигнала с другим «четким» сигналом, то это не так страшно. Плохо, когда на нейронах-детекторах выделяется «размытый» образ, удобный для сравнения. В этом случае происходит необратимая потеря информации.
Выход воспоминания
В примерах MNIST цифры не имеют фона, свободны от шумов и приходятся по одной на картинку. В более сложных задачах кроме целевого объекта на изображении или в описании может содержаться дополнительная информация. За счет этого в сложных задачах проще говорить не о точном или высоком совпадении, а о том, является ли величина совпадения случайной или же в двух описаниях есть нечто, позволяющее говорить об их определенном сходстве.
При распознавании цифр надо оценить к какой цифре ближе текущий образ. Для этого можно вычислить среднее значение совпадения текущего образа с воспоминаниями, относящимися к каждой из цифр. Такая оценка усредненного совпадения хотя и будет нести определенный смысл, будет плоха для принятия решения. Например, класс двоек содержит как минимум два варианта написания — с «петелькой» внизу и без нее. Еще хуже ситуация, например, с написанием букв. К одному классу могут относится как заглавные так и строчные написания одной буквы.
В таких случаях разумно усреднять примеры раздельно для каждого из вариантов написания. То есть имеет смысл предварительно провести кластеризацию среди воспоминаний, относящихся к одному классу, и разбить их на соответствующие группы.
Кроме того, если нужный образ только часть воспоминания, то надо учитывать этот факт. Хотелось бы, чтобы выход воспоминания давал оценку именно «полезного» совпадения, а не того, какая часть воспоминания совпала. Например, отойдем от тепличного MNIST и предположим, что в обучающем примере было сразу две цифры, двойка и тройка, написанные рядом. Мы сдвинули изображение так, чтобы двойка совпала с другими запомненными двойками. Но в созданном воспоминании тройка останется, как находящийся рядом шум. Сравнивая потом это воспоминание с образом, где есть двойка, хотелось бы, чтобы шум не влиял на величину оценки совпадения.
Активация выходных нейронов
Каждый выходной нейрон получает информацию о том, какие есть воспоминания, в которых нашлось что-то общее с входным сигналом, и информацию об уровне этих совпадений. Из этой информации надо сделать вывод о том, какова вероятность, что перед нами тот образ, на который происходило обучение. Из сравнения вероятности для всех выходных нейронов надо принять решение, какой из них предпочтительнее и достаточен ли вообще уровень достигнутой вероятности для появления выходного сигнала.
Бинарное кодирование выхода сети
Допустим, что нам удалось разрешить все сложности и создать такие воспоминания и выходные нейроны, которые позволяют уверенно проводить обучение с учителем и последующее распознавание. Теперь зададимся вопросом — сколько нейронов должно быть в выходном слое? В классических нейронных сетях и в той сети, что мы описали выше, ответ очевиден — столько, сколько планируется выходных признаков.
Ранее мы говорили, что в реальном мозге одна миниколонка коры, состоящая из порядка ста нейронов, выполняет функции контекстного вычислительного модуля. То есть производит анализ того, как выглядит информация в контексте именно этой миниколонки. Каждая миниколонка имеет собственную копию памяти и способна вести полную обработку информации независимо от остальных миниколонок. Это значит, что одна миниколонка должна выполнять все функции, которые свойственны нейронным сетям. При этом количество признаков, с которыми сталкивается миниколонка значительно больше ста и может составлять десятки или сотни тысяч.
Сто нейронов кодируют сто признаков, когда разговор идет о нейронах-детекторах и о признаковых описаниях. Но мы исходим из того, что нейроны не формируют признаковых описаний, а своей активностью создают сигналы бинарного кода, которыми кодируются те или иные понятия.
Несложно модифицировать нейронную сеть, чтобы ее выход кодировал не признаковое описание, а бинарный код признака. Для этого надо «соединить» воспоминания не с одним выходным нейроном, а с несколькими, образующими соответствующий код. Например, цифры от 0 до 9 можно закодировать пятибитным кодом так, чтобы в каждом коде было ровно две единицы (рисунок ниже). Тогда каждое воспоминание будет воздействовать не на один, а на два нейрона. Результатом работы такой сети будет не активность одного нейрона, соответствующего цифре, а нейронный бинарный код цифры. При таком кодировании нейроны перестают быть нейронами бабушки, так как их активность может проявляться в совершенно разных понятиях.

Кодирование выхода сети бинарным кодом
Если мы посмотрим на сеть, которая получилась в результате, то окажется, что она уже мало напоминает традиционные нейронные сети, хотя и полностью сохраняет всю их функциональность.
Посмотрим на получившуюся сеть в разрезе сформулированных ранее шести принципов классической нейронной сети:
Принцип 1. Каждый нейрон — это детектор некого свойства.
Не выполняется. Выходные нейроны не являются нейронами бабушки. Один и тот же нейрон срабатывают на разные признаки.
Принцип 2. Информация в нейронной сети — это признаковое описание.
Не выполняется. Выход сети — это код понятия, а не набор признаков. Вход сети также может работать с кодами, а не с векторами признаков.
Принцип 3. Нейронная сеть, как правило, — это преобразователь признаковых описаний.
Не выполняется.
Принцип 4. Количество нейронов в сети определяет число признаков, с которыми может работать эта сеть.
Не выполняется. Выходной слой, содержащий сто нейронов, при кодировании сигнала десятью активными нейронами может отобразить 1.7×1013 различных понятий.
Принцип 5. Обучение сети — это настройка весов соединяющих нейроны связей.
Не выполняется. Воспоминания имеют «привязку» к нейронам, но никакого адаптивного изменения весов не происходит.
Принцип 6. Конечность обучения. Дилемма стабильности-пластичности.
Не выполняется. Как бы не была обучена сеть ее можно всегда дообучить просто добавив новые воспоминания. При добавлении не требуется учитывать скорость обучения. Разрушения старой информации не происходит. Кроме того, новая сеть способна на «однострельное обучение». Единичный опыт в любой момент обучения создает способность узнавать соответствующее явление. В отличие от традиционных сетей не требуется многократного повторения, так как нет процедуры итерационной настройки весов нейронов-детекторов.
Миниколонки коры
Основные информационные процессы нашего мозга происходят в его коре. Кора мозга делится на зоны. Каждая зона состоит из сотен тысяч одинаковых по строению миниколонок. Количество нейронов в миниколонке в зависимости от типа зоны от 100 до 200.
Нейроны одной миниколонки расположены друг под другом. Большая часть их связей сосредоточена в вертикальном направлении, то есть с нейронами своей же миниколонки.
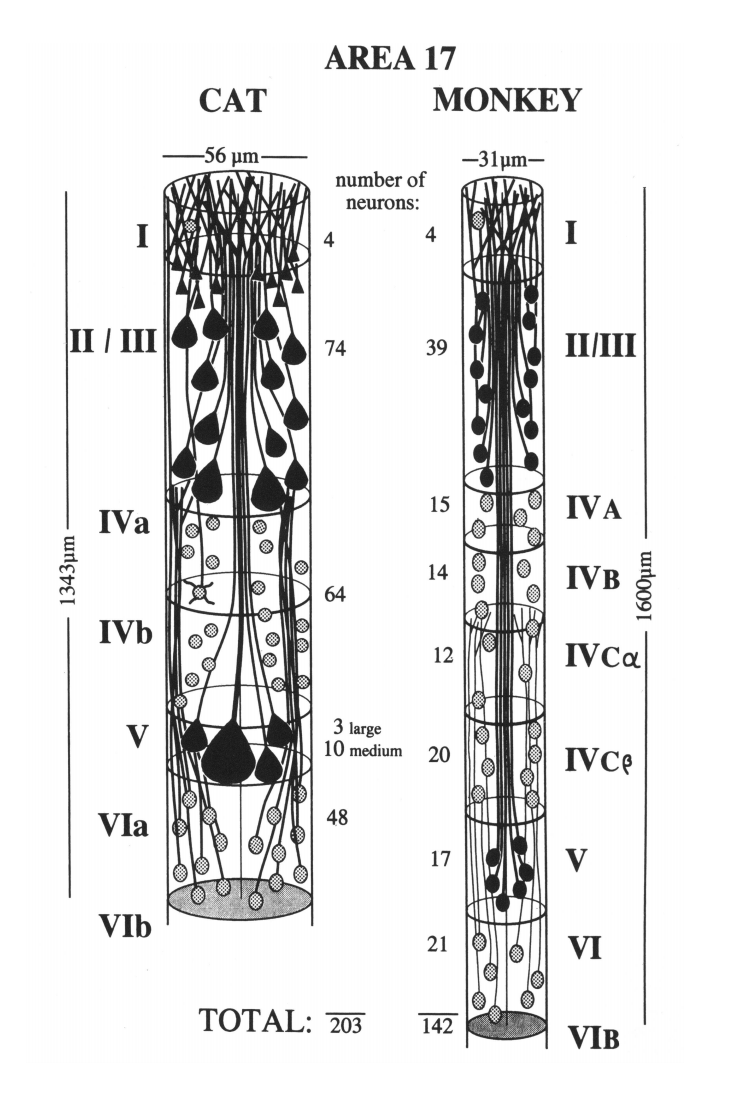
Миниколонки первичной зрительной коры кошки (слева) и обезьяны (справа) (Peters and Yilmaze, 1993)
Ранее было сделано предположение, что каждая миниколонка коры соответствует отдельному контексту. Миниколонки какой-либо зоны коры позволяют рассмотреть одну и ту же входную информацию во всех возможных для этой зоны контекстах и определить, какой из них лучше подходит для трактовки поступившей информации.
Информация распространяется по всему пространству зоны коры, например, с помощью волн с самопрод
