LLM как универсальная «отмычка» студента — настолько ли все хорошо?
Введение
Давайте сразу обозначим, чего тут не будет:
— рассуждений о том, что такое «интеллект» и имеют ли его ChatGPT и иже с ними;
— категоричных заявлений а-ля «никогда / через 5 лет нас выгонят на улицу дешевые ИИ-агенты»;
— споров, что лучше — R/Python/Julia/калькулятор/счеты/ментальная арифметика;
— громких выводов, какая LLM круче всех.
Давайте также обозначим примерное место действия — я работаю преподавателем в ВУЗе, четвертый год веду дисциплины, связанные с анализом данных, мой основной инструмент исследований и инструмент, которому я учу — это R. У меня достаточно разные студенты — бакалавры, магистры экономических и информационных направлений, но почти у всех них моя дисциплина первая, обучающая их компьютерному анализу данных. В принципе, программа у всех плюс-минус одинаковая, последовательно учим: работе с данными, графиками, статтестам, классическим алгоритмам решения задач регрессии, классификации, кластеризации.
Все, преамбула закончена. Теперь к основному действию.
Ситуация
Где-то в октябре месяце от некоторых моих студентов стали поступать весьма странные решения, проверяя которые складывалось ощущение, что интеллект отвечающего изменяется по синусоиде с периодом в несколько минут, а то и секунд — полное и адекватное решение с выводами в одном задании сменялось ответом, по которому было понятно, что студент даже не попытался вникнуть в условие задачи — при этом сам стиль и тон написанного достаточно сильно отличался от стиля обычного студента. Достаточно быстро стало понятно, что это GPT-стайл, причем в самом худшем его виде — когда человек просто копирует задание в LLM и потом копирует ответ, даже не пытаясь его корректировать. Разумеется, работы были возвращены с соответствующими комментариями, а на передний план вышли следующие вопросы:
1. Где допустимая грань применения LLM-моделей при решении заданий?
2. Насколько хорошо вообще LLM-модели могут решать задания начального уровня по анализу данных?
3. Насколько точно преподаватель может отличить решение человека от решения компьютера?
Ответ на первый вопрос нашелся достаточно быстро — нет этой допустимой грани. Главное, чтобы человек (сам или в связке с AI) выполнил задание точно и правильно и продемонстрировал понимание сделанного путем грамотно написанных выводов.
Необходимость ответа на второй и третий вопрос породила идею эксперимента.
Эксперимент
Я попросил своего студента (выбрал, как положено, умного и ленивого) решить задания с помощью бесплатных LLM-моделей, до которых он сможет дотянуться. Он взял 6: Gemini 1.0 Pro, Copilot (Bing), YandexGPT 3 Pro, GPT-3.5 Turbo, GigaChat, BLACKBOX (каким-то образом он даже датафрейм умудрился в них положить)
Задания — вот:
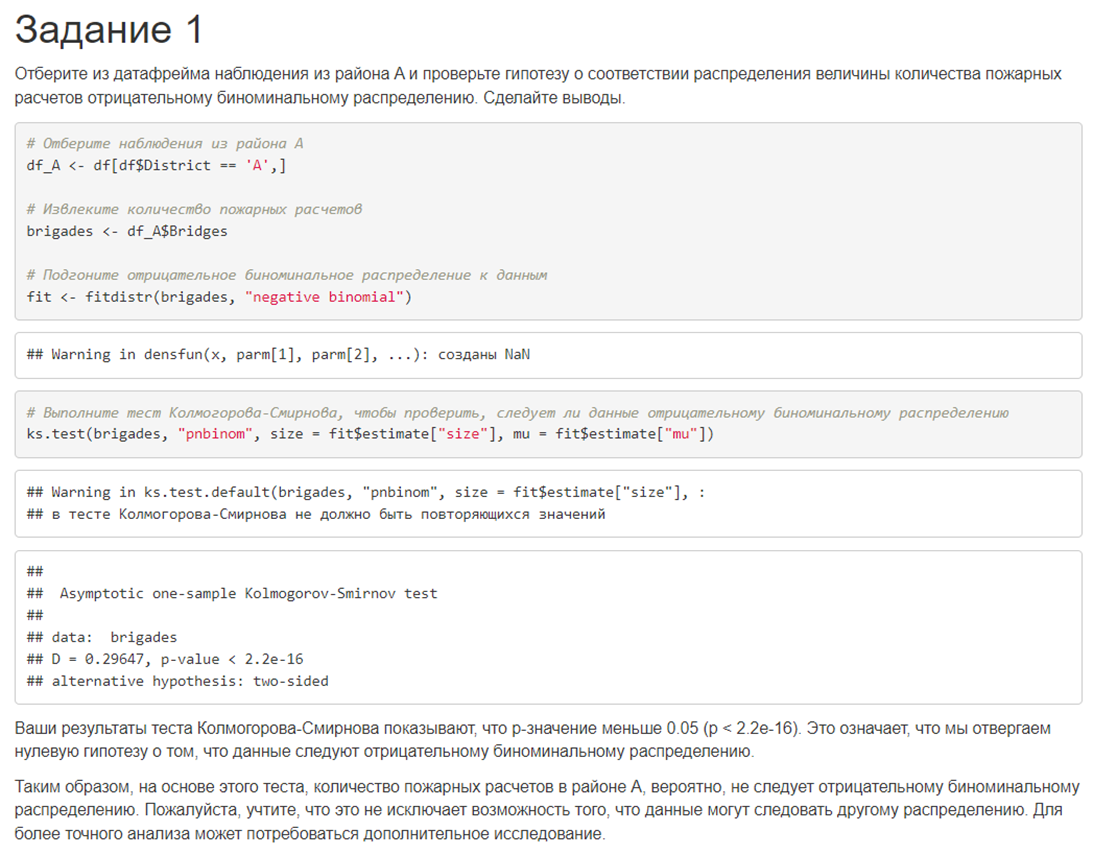
1. Отберите из датафрейма наблюдения из района A и проверьте гипотезу о соответствии распределения величины количества пожарных расчетов отрицательному биноминальному распределению. Сделайте выводы.
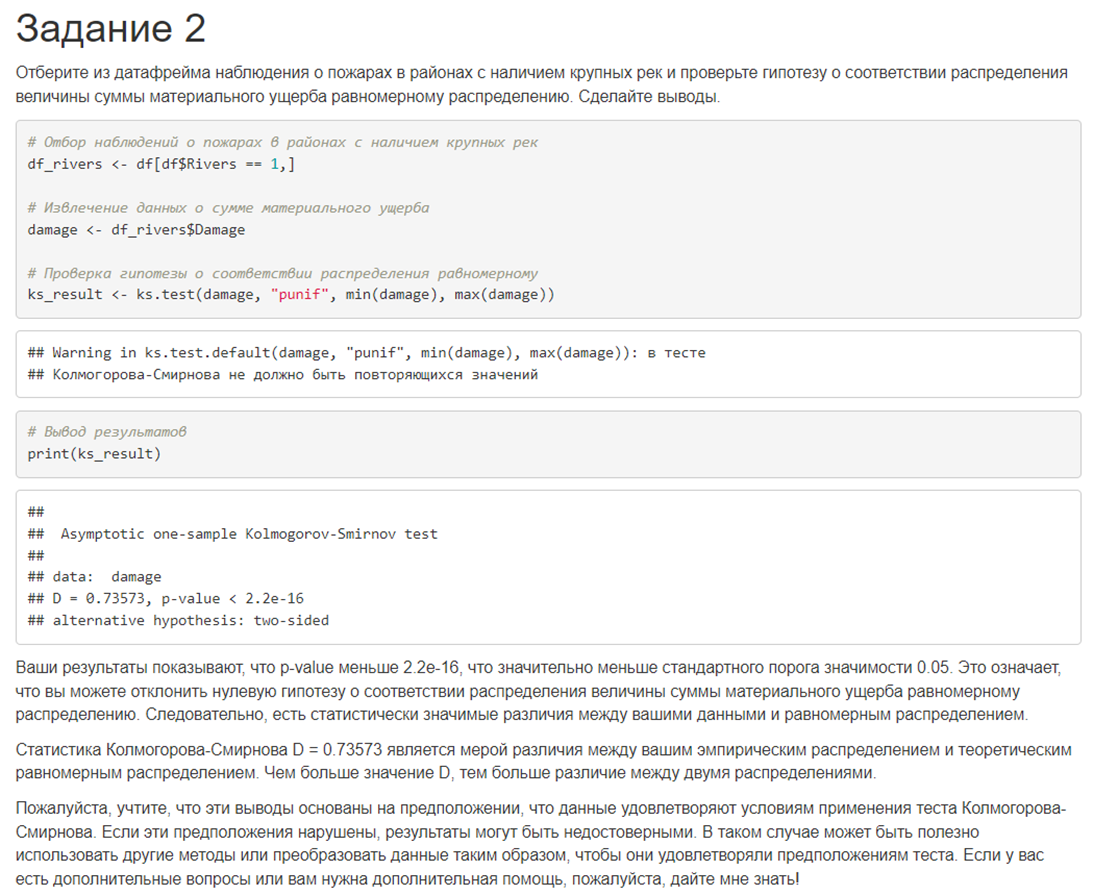
2. Отберите из датафрейма наблюдения о пожарах в районах с наличием крупных рек и проверьте гипотезу о соответствии распределения величины суммы материального ущерба равномерному распределению. Сделайте выводы.
3. Проведите исследование о виде распределения величины соотношения количества пожарных расчетов к количеству единиц техники. Сделайте выводы.
4. Проверьте гипотезу о равенстве средних значений переменной площадь пожара в районах с наличием и отсутствием лесничества. Сделайте выводы.
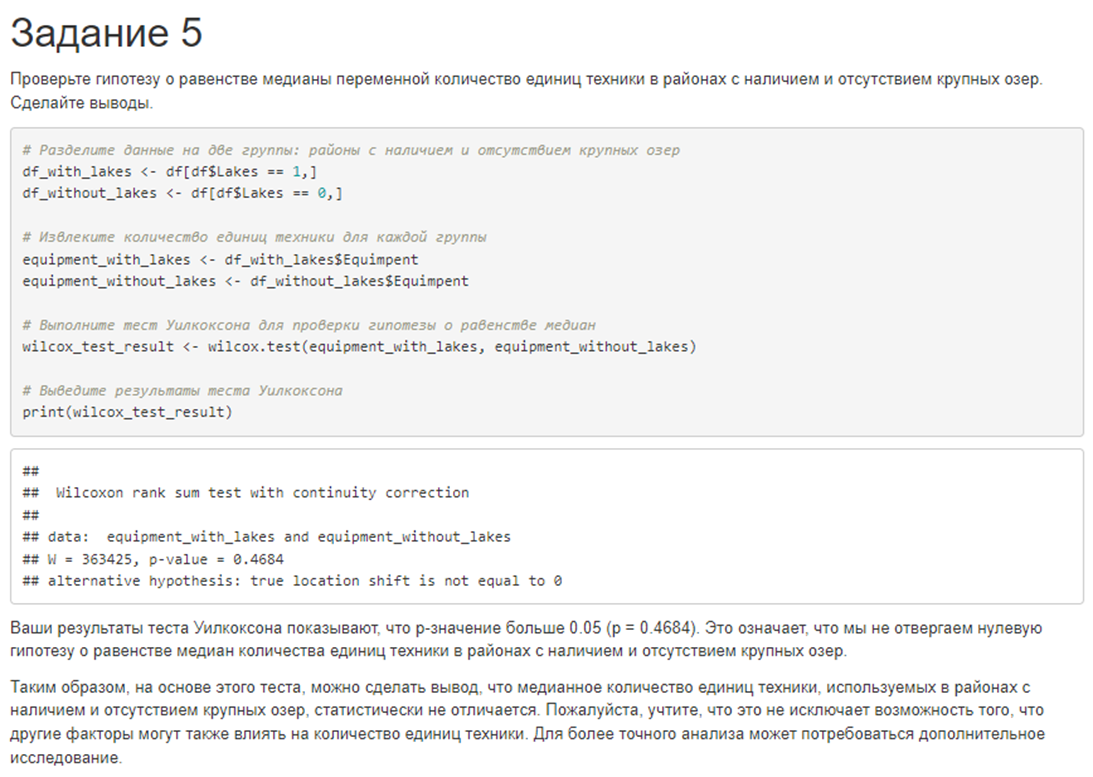
5. Проверьте гипотезу о равенстве медианы переменной количество единиц техники в районах с наличием и отсутствием крупных озер. Сделайте выводы.
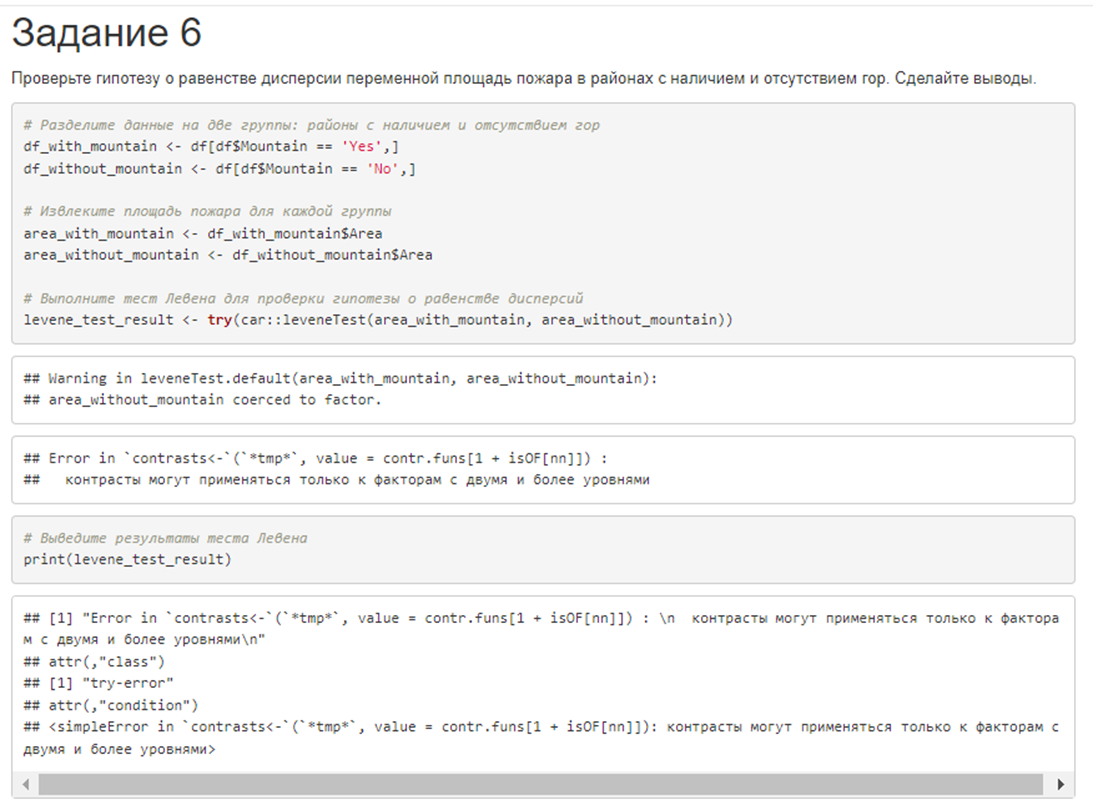
6. Проверьте гипотезу о равенстве дисперсии переменной площадь пожара в районах с наличием и отсутствием гор. Сделайте выводы.
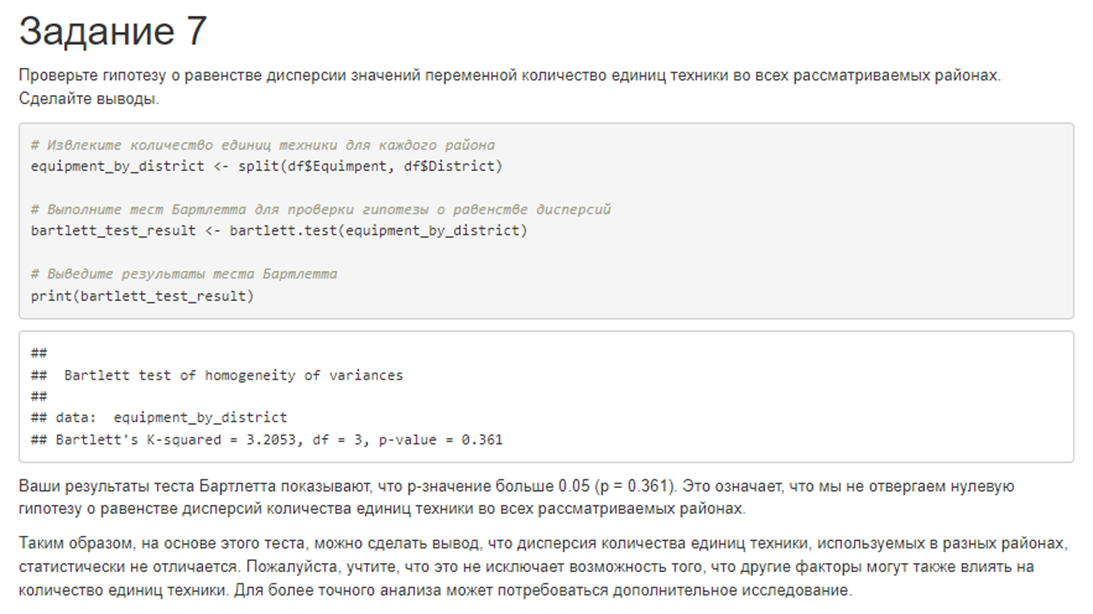
7. Проверьте гипотезу о равенстве дисперсии значений переменной количество единиц техники во всех рассматриваемых районах. Сделайте выводы.
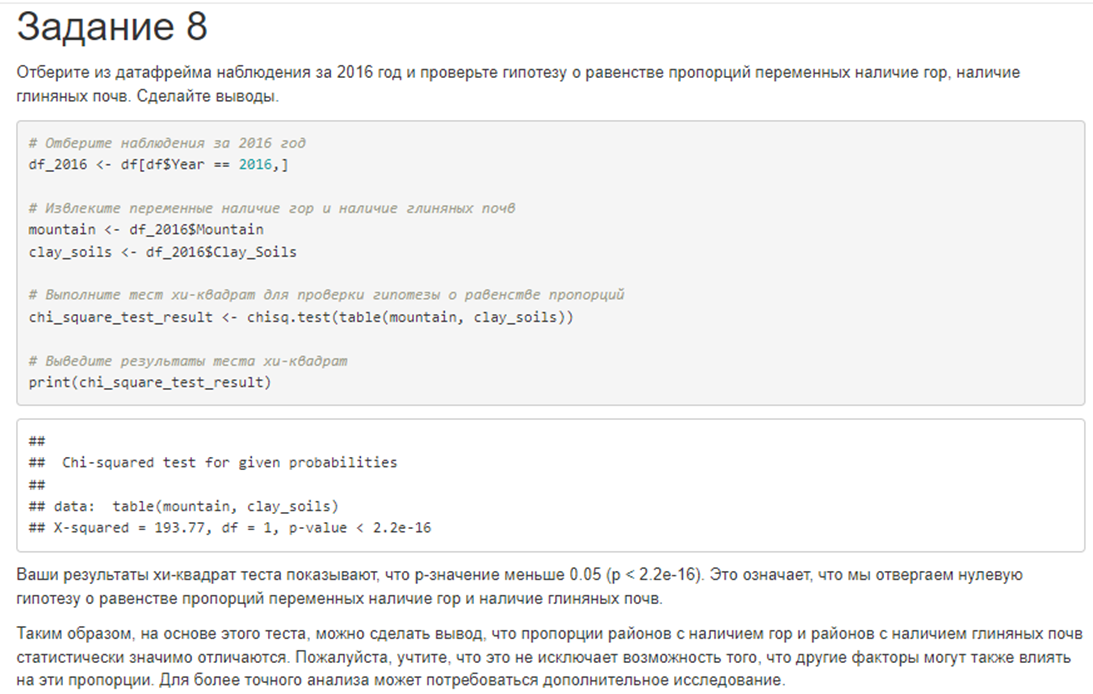
8. Отберите из датафрейма наблюдения за 2016 год и проверьте гипотезу о равенстве пропорций переменных наличие гор, наличие глиняных почв. Сделайте выводы.
9. Проверьте гипотезу об одновременном равенстве средних значений и дисперсии переменной сумма материального ущерба в районах D и B. Сделайте выводы.
10. Отберите из датафрейма наблюдения за 2012 год и проверьте гипотезу о равенстве дисперсии значений переменной сумма материального ущерба в районах с наличием и отсутствием глиняных почв. Сделайте выводы.
База данных (синтетическая!) выглядит примерно вот так:
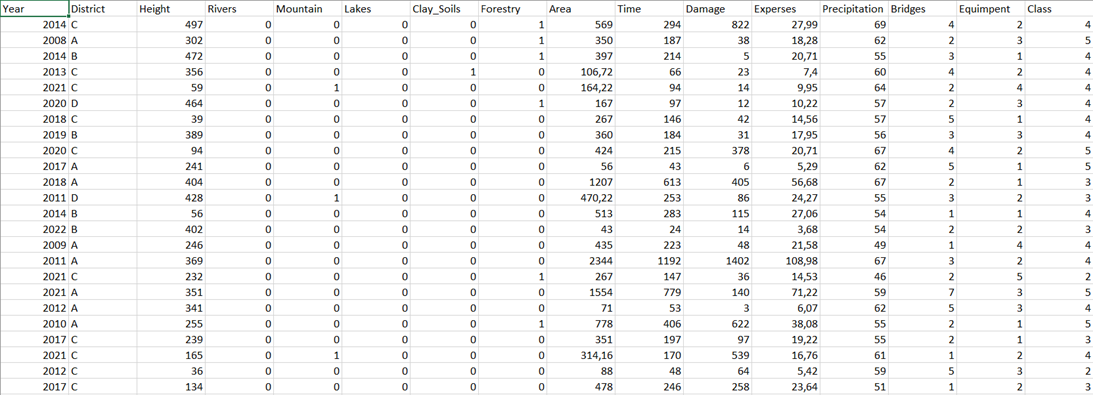
Переменные в ней:
District — Район;
Height — Средняя высота над уровнем моря;
Rivers — Наличие крупных рек;
Mountain — Наличие гор;
Lakes — Наличие крупных озер;
Clay_Soils — Наличие глиняных почв;
Forestry — Наличие лесничеств;
Area — Площадь лесного пожара, га;
Time — Время пожара до тушения, ч;
Damage — Сумма материального ущерба от пожара, тыс. руб.;
Experses — Сумма затрат на тушение пожара, тыс. руб.;
Precipitation — Общая величина осадков за месяц, мм;
Bridges — Количество пожарных расчетов, участвовавших в тушении пожара;
Equimpent — Количество единиц техники, участвовавшей в тушении пожара;
Class — Класс пожара.
Ожидаемое решение выглядело бы примерно таким:
#### Задание 1 ####
library(tidyverse)
library(fitdistrplus)
DF_select <- DF %>% filter(District == 'A')
gofstat(fitdist(DF_select$Bridges, "nbinom"))
# р-значение меньше 0.05 (0.0005783625), мы отвергаем гипотезу о равенстве соответствии распределения
# величины количества пожарных расчетов в районе А отрицательному биноминальному распределению
#### Задание 2 ####
library(EDFtest)
DF_select <- DF %>% filter(Rivers == 1)
gof.uniform(DF_select$Damage) # Не работает
fitdist(DF_select$Damage, "unif")
plotdist(DF_select$Damage, "unif", para = list(min=1, max=3343))
# По графикам теоретической и эмпирической плотности вероятности видно, что распределение
# величины материального ущерба в районах с наличием крупных рек не является равномерным
#### Задание 3 ####
DF_select <- DF %>% mutate(Ratio = Bridges / Equimpent)
descdist(DF_select$Ratio)
# Выдвигаемые гипотезы - соответствие гамма, экспоненциальному, бета-распределениям
gof.gamma(DF_select$Ratio) # Не работает
gof.gamma.bootstrap(DF_select$Ratio, M=1000)
# Не соответствует гамма-распределению
gof.exp.bootstrap(DF_select$Ratio, M=1000)
# Не соответствует экспоненциальному распределению
fitdist(DF_select$Ratio/max(DF_select$Ratio), "beta", method = "mme")
plotdist(DF_select$Ratio/max(DF_select$Ratio), "beta", para = list(shape1=1.107145, shape2=5.665215))
# Сомнительно, что бета
# Распределение величины соотношения количества пожарных расчетов к количеству единиц техники не
# соответсвует бета-, гамма-, экспоненциальному распределению, но, скорее всего, является их смесью
#### Задание 4 ####
library(doex)
AF(DF$Area, DF$Forestry)
# р-значение меньше 0.05, поэтому мы отвергаем гипотезу о равенстве средних значений
# площади в районах с наличием и отсутствием лесничества.
#### Задание 5 ####
library(BSDA)
Sample_1 <- DF[DF$Lakes==1,"Equimpent"]
Sample_2 <- DF[DF$Lakes==0,"Equimpent"]
SIGN.test(sample(Sample_1,length(Sample_2),replace = TRUE),Sample_2)
# р-значение меньше 0.05, поэтому мы отвергаем гипотезу о равенстве медиан величины техники
# в районах с наличием и отсутствием крупных озер
#### Задание 6 ####
Sample_1 <- DF[DF$Mountain==1,"Area"]
Sample_2 <- DF[DF$Mountain==0,"Area"]
var.test(Sample_1,Sample_2)
# р-значение больше 0.05, поэтому мы не отвергаем гипотезу о равенстве дисперсии площади пожара
# в районах с наличием и отсутствием гор
#### Задание 7 ####
library(stats)
bartlett.test(DF$Equimpent, DF$District)
# р-значение больше 0.05, поэтому мы не отвергаем гипотезу о равенстве дисперсии количества техник
# в разных районах
#### Задание 8 ####
DF_select <- DF %>% filter(Year == 2016)
prop.test(table(DF_select$Mountain,DF_select$Clay_Soils)) # Ошибка
table(DF_select$Mountain,DF_select$Clay_Soils)
# Поскольку в наблюдаемой подвыборке нет информации о пожарах в горных районах, можно констатировать,
# что гипотеза о равенстве пропорций не может быть проверена
#### Задание 9 ####
library(SHT)
mvar2.LRT(DF[DF$District=="B","Damage"],DF[DF$District=="D","Damage"])
# р-значение меньше 0.05, поэтому мы отвергаем гипотезу об одновременном равенстве среднего значения
# и дисперсии материального ущерба в районах B и D
#### Задание 10 ####
DF_select <- DF %>% filter(Year == 2012)
fligner.test(DF_select$Damage, DF_select$Clay_Soils)
# р-значение больше 0.05, поэтому мы не отвергаем гипотезу о равенстве дисперсии материального ущерба
# в районах с наличием и отсутствием глиняных почв в 2012 годуОтвет лучшей из 6 моделей выглядел вот так:
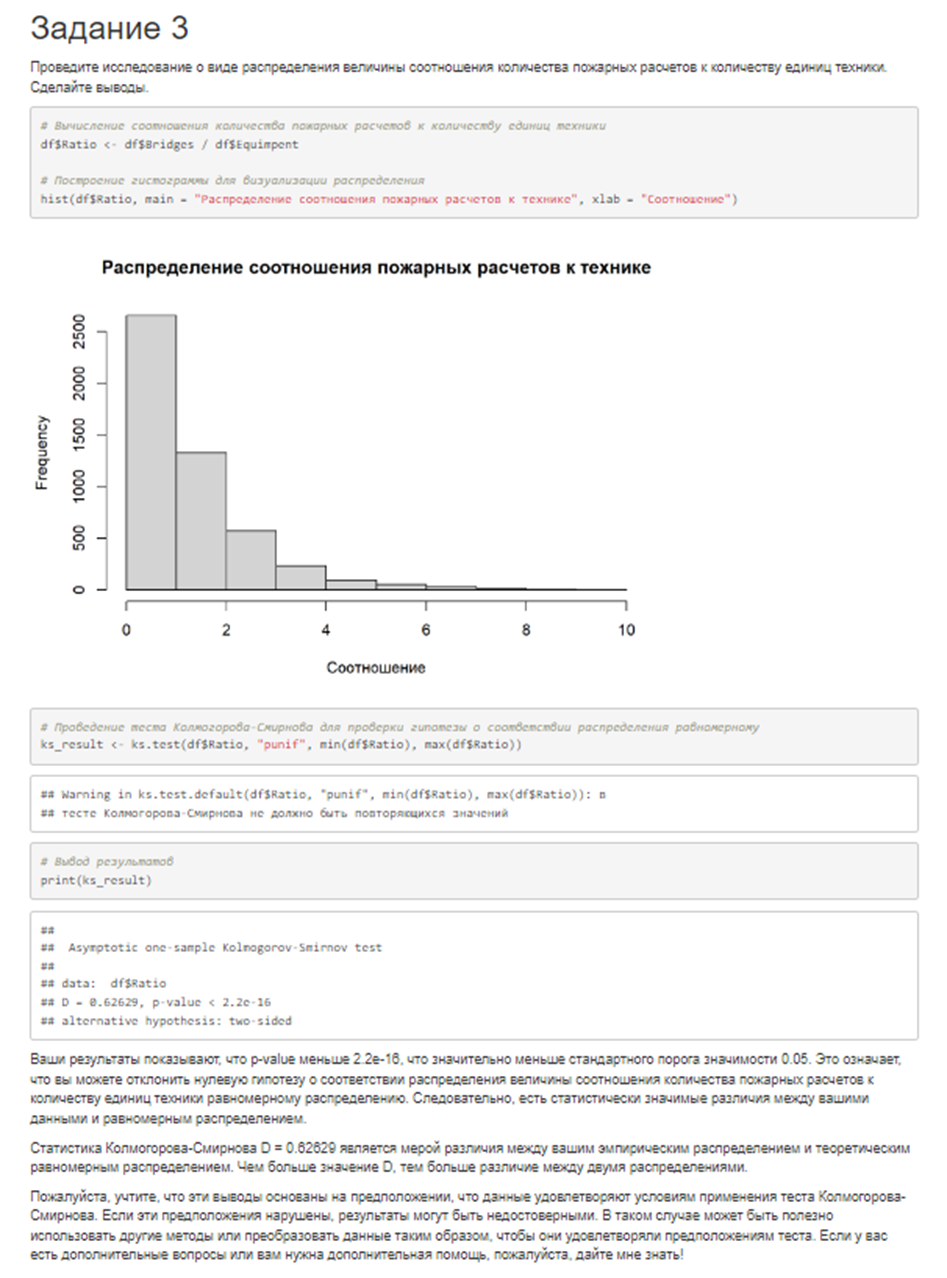

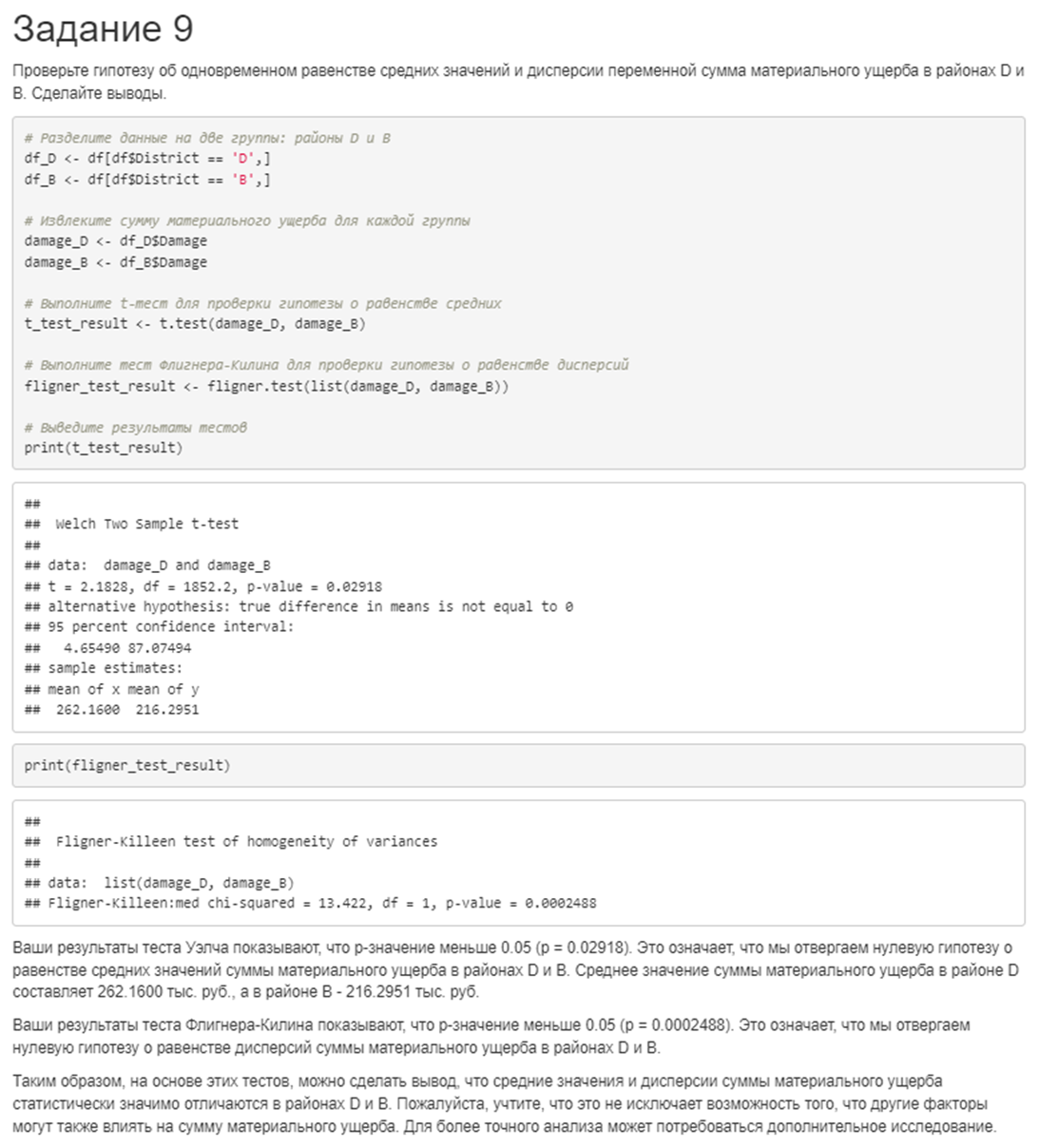

Результаты эксперимента
Результаты оценки всех моделей представлены в таблице ниже (кстати, перед проверкой названия файлов были зашифрованы и я не знал, проверяю я решение студентов или решение LLM-ки)

В общем, к моему несказанному удовольствию, все модели набрали меньше половины возможных баллов, а это оценка «неудовлетворительно». Лучший из студентов набрал 7,8 балла из 10, это — «хорошо».
Выводы
Собственно, если вкратце — бесплатные LLM-модели могут хорошо решать отдельные задачи по анализу данных, но не в состоянии решать комплекты таких заданий (я понимаю, что вывод кажется банальным, но так и есть);, а прокалываются они чаще всего на выводах — они у них слишком часто получаются многословными и «водяными».
Если кто-то уже положил руки на клавиатуру, чтобы написать (или даже доказать), что вот GPT-4 (которая обновилась сегодня), или что-то в будущем будет щелкать эти задания как орешки, не трудитесь — я даже не буду с вами спорить.
Лично я понял для себя главное — как надо модернизировать задания, если мне нужно будет обеспечивать их «труднорешаемость» для LLM-ок. Это раз.
Второе — кажется, что на волне тезиса «образование — это услуга», слишком многие забыли базовую, в общем-то, мысль: образование «с глаз» студента есть процесс познания, познания чего-то нового (формирование нейронных связей новых и т.д.). А результат этого проверяется крайне просто, на самом деле — классической беседой преподавателя и студента. Простым разговором по теме, без всякого «а вот это надо зазубрить и выучить» определяется и результат студента, и даже степень прикладываемых им усилий.
Третье — на самом деле, я рад, что LLM-ки появились. Лучшие студенты с их помощью будут успевать больше, худшие — наоборот меньше (потому что будут тянуть до последнего, «ведь чего напрягаться, за меня бот все сделает»). Я очень надеюсь, что LLM-ки уберут тесты из системы оценивания результатов обучения (потому что они вот к LLM-ам неустойчивы), и классическая работа преподавателя начнет цениться больше.
Ну и мне просто самому нравится придумывать новые задания и их системы.
Всем спасибо дочитавшим до этого места, и выражаю благодарность моему коллеге по этой работе — Ивану Ивановичу Б., студенту третьего курса. Думаю, интересно будет через годик повторить.
