LIFT: Learned Invariant Feature Transform

Введение
В последние годы вездесущие нейронные сети находят все больше и больше применений в различных областях знаний, вытесняя классические алгоритмы, использовавшиеся многие годы. Не стала исключением и область компьютерного зрения, где год за годом все больше и больше задач решаются при помощи современных нейронных сетей. Настало время написать об еще одном павшем бойце в войне «Традиционное зрение vs. Глубокое Обучение». Долгие годы на задаче поиска локальных особенностей изображений (так называемых ключевых точек) безраздельно властвовал алгоритм SIFT (Scale-invariant Feature Transform), предложеный в далеком 1999 году, многие сложили головы в попытках превзойти его, но удалось это лишь Deep Learning’у. Итак, встречайте, новый алгоритм поиска локальных особенностей — LIFT (Learned Invariant Feature Transform).
Need for Data

Чтобы глубокое обучение заработало, нужно много данных, иначе магии не получится. А нужны нам не всякие данные, а такие, которые бы являлись репрезентативным представлением той задачи, которую мы хотим решать. Итак, давайте посмотрим на то, что умеют рукотворные детекторы/дескрипторы особых точек:
- Инвариантность к расположению на картинке.
- Инвариантность к углу поворота.
- Инвариатность к масштабу.
Окей, значит нам нужен датасет, содержащий кучу точек, где для каждой особой точки будет много сэмплов, полученных с разных ракурсов. Можно, конечно, взять произвольных картинок, нарезать с них точек, а затем применяя синтетически сгенерированные афинные преобразования получить датасет сколь угодно большого размера. Но синтетика плоха тем, что всегда есть некоторые ограничения по точности моделирования
реальных кейсов. Реальные наборы данных, удовлетворяющих нашим требованиям, возникают при решении некоторых прикладных задач компьютерного зрения. Например, при 3D реконструкции сцен, снятых с нескольких ракурсов, мы делаем примерно следующее:
- Для каждого изображения сцены находим особые точки.
- Находим соответствия между особыми точками с разных изображений.
- Но основе этой информации вычисляем пространственное расположение каждого кадра (параметризуемое через
т.е. поворот и трансляцию относительно начала координат).
- При помощи процедуры триангуляции находим 3D положения всех особых точек.
- Используя развесистую оптимизацию аки Bundle Adjustment (чаще всего алгоритм, производные от метода Левенберга-Марквардта), получаем более точную информацию о расположении точек в пространстве.
- Всякий разный постпроцессинг. Например, можно натянуть полигональную модель на облако точек, для получения гладких поверхностей.
Как побочный продукт работы такого алгоритма, мы получаем облако точек, где каждой 3D точке соответствует несколько её 2D положений (проекций) на кадрах сцены. Вот такое облако — это как раз тот датасет, который нам нужен. Особо не заморачиваясь тонкостями Structure From Motion, авторы работы взяли пару имеющихся в публичном доступе датасетов для 3D реконструкции, прогнали их через публично доступный инструмент для построения облака точек (VisualSFM), и далее в своих экспериментах пользовались полученным набором данных. Как утверждается, натренированная на таком наборе сетка также обобщается и на другие типы сцен.
Сетки, сетки, сетки
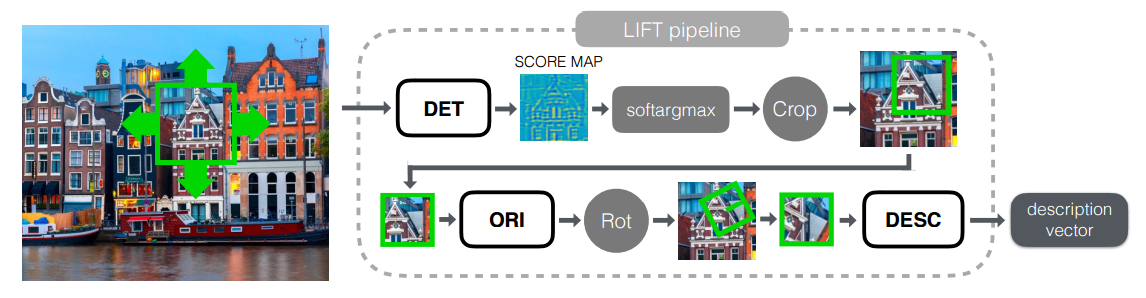
С датасетом мы разобрались, поэтому пора переходить к самому интересному, а именно — изучению сеток. Всю сетку можно разделить на 3 логических блока:
- Detector — отвечает за поиск особых точек на всем изображении в целом.
- Rotation Estimator — определяет ориентацию точки и доворачивает патч вокруг неё так, чтобы угол поворота стал равен нулю.
- Descriptor — принимает на вход патч, по которому строит уникальный (тут как получится) вектор, описывающий этот патч. Эти вектора уже можно использовать, например, для того, чтобы посчитать Евклидово расстояние между парой точек и понять, похожи они или нет.
Сначала рассмотрим инференс для этой модели в целом, а затем все блоки по отдельности и как именно они тренируются.
Inference
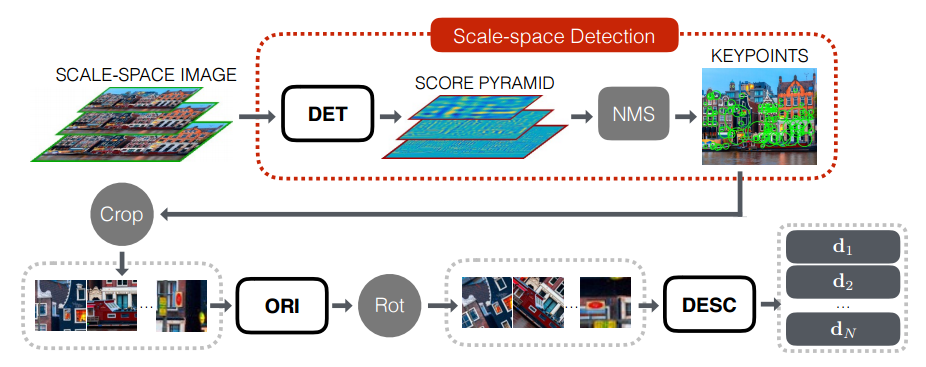
Поиск особых точек и вычисление их дескрипторов происходит в несколько этапов:
- Для начала строим пирамида для исходного изображения.
- Каждый слой пирамиды прогоняем через сеть-детектор и вычисляется пирамида Score Map’ов.
- При помощи процедуры Non-Maximum Suppression находим наиболее сильные кандидаты в особые точки.
- Для каждой особой точки вырезаем патч, включающий в себя особую точку и некоторую её окрестность.
- Выравниваем ориентацию каждого патча при помощи Orientation Estimator’а.
- Вычисляем дескриптор для каждого выровненного патча.
Descriptor
Еще со времен SIFT-фич известно, что даже если мы не особо хорошо умеем находить действительно уникальные точки, но можем построить для каждой из них крутой дескриптор, то скорей всего поставленную задачу мы решить сможем. Поэтому, начнем обзор с конца, а именно с построения дескриптора для уже найденной особой точки. Вообще говоря, любая сверточная сетка, принимая на вход картинку (патч), на выходе выдает некое описание этой картинки, которое уже можно использовать в качестве дескриптора. Но, как показывает практика, нет нужды брать огромную сеть, такую как, например, VGG16, ResNet-152, Inception etc., нам достаточно и маленькой сети: 2–3 сверточных слоя с активациями в виде гиперболических тангенсов
и прочей мелочовки типа батч нормализаций и т.п.
Для определенности, обозначим нашу дескриптор-сеть , где
— сверточная сеть дескриптора,
— её параметры,
— патч с нулевым углом наклона (полученый от Rotation Estimator’а).
Для каждой особой точки составим две пары:
— пара патчей, соответствующих проекциям одной и той-же особой точки.
— пара патчей, где первый принадлежит особой точке, а второй (негативный семпл) нет. При этом, «негативный» патч выбирается из некоторой окрестности, не слишком далекой, от позитива. В процессе тренировки окрестность уменьшается, чтобы негативные семплы становились все сложнее.
В процессе обучения будем минимизировать loss-функцию следующего вида:
Т.е. по сути мы хотим, чтобы Евклидово расстоянием между похожими точками было небольшим, а между не похожими друг на друга точками было далеким.
Rotation Estimator
Так как мы можем наблюдать одну и ту же точку не только из разных точек пространства, но и под разными углами наклона, мы должны уметь строить одинаковый дескриптор для одной и той же особой точки, независимо от того, с какого угла мы её наблюдаем. Но вместо того, чтобы учить Descriptor запоминать все возможные углы наклона для одной и той же точки, предлагается использовать промежуточный вычислительный блок, который будет определять ориентацию патча в пространстве (Rotation Estimator) и «доворачивать» патч до некоторого своего инвариантного к повороту состояния (Spatial Transform). Конечно, можно было бы воспользоваться блоком вычисления ориентации патча в пространстве, взятым из алгоритма построения SIFT фич, но за окном 21 век и теперь принято всякую задачу компьютерного зрения сводить к машинному обучению. Вот и мы воспользуемся еще одной сверточной нейронной сетью для решения этой задачи.
Итак, обозначим нашу нейронную сеть как: , где
— параметры сети, а
— исходный патч.
В качестве обучающе выборки возьмем пары патчей ,
, принадлежащих одной особой точке, но имеющие разные углы наклона, а так-же их пространственные координаты
,
.
В процессе обучения будем минимизировать следующую loss-функцию:
где — патч, полученный после процедуры коррекции его ориентации,
.
Т.е. при обучении сети, мы доворачиваем патчи, с разным углом наклона, так, чтобы Евклидово расстояние между их дескрипторами стало минимальным.
Detector
Осталось рассмотреть последний шаг, а именно непосредственное детектирование особых точек на исходном изображении. Суть этой сети в том, что через неё прогоняется все изображение целиком, и на выходе ожидается некоторая карта особенностей (feature map), для которой сильным откликам соответствуют особые точки на исходном изображении.
Несмотря на то, что при инференсе модели, детектор запускается на всем изображении сразу, в процессе тренировки мы будем прогонять его только для отдельных патчей.
Вычисление детектора состоит из двух шаго: сначала мы должны вычислить Score Map для патча, по которой далее будет определяться позиция особой точки:
а затем, вычислить положение особой точки:
где — это функция, вычисляющая взвешенный центр масс с весами, являющимися результатом вычисления
:
где y — позиция внутри Score Map’ы, — гиперпараметр, отвечающий за коэффициент «размытия» softmax-функции.
При тренировке детектора будем брать по четыре патча , где
— проекции одной и той-же особой точки,
— проекция другой особой точки,
— патч не принадлежащий особой точке. Для набобра таких патчей будем минимизировать следующую loss-функцию:
где — параметр балансировки для двух членов loss-функции.
Член лосса, отвечающий за корректную классификацию на позитивы и негативы:
Член лосса, отвечающий за точную локализацию особых точек:
Тренировка
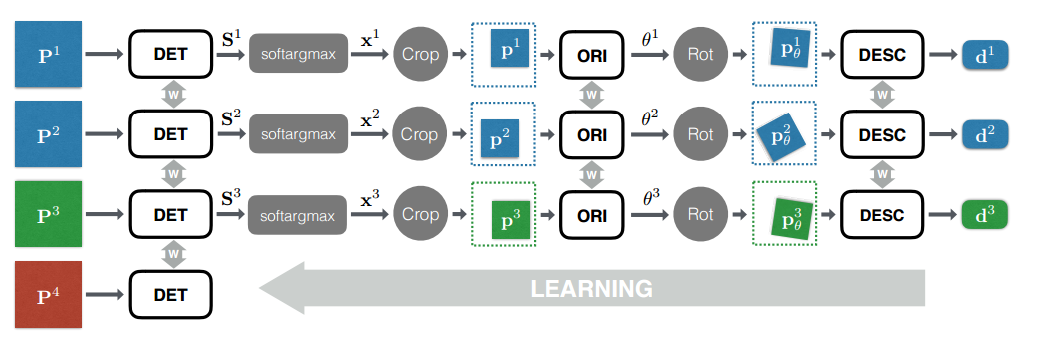
Вся сеть тренируется в модной нынче манере End-To-End, т.е. сразу учатся все части сети параллельно как сиамские сети. При этом для каждого из 4-х, используемых при тренировке, патчей создается отдельный бранч сети с шаррингом весов между ними.
Эксперименты
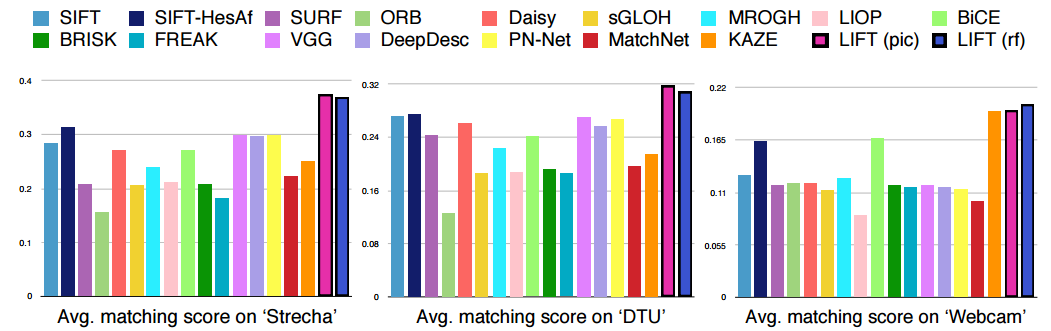
Сравнив с имеющимися ранее методами нахождения особых точек, авторы пришли к выводу, что их подход является state of the art.
А результаты работы их сети можно посмотреть на следующем видео:
Заключение
Представленая работа — очередное подтверждение того, что уходит время традиционных методов компьютерного зрения, а на смену ему приходит эпоха дата сайнса. И в очередной раз придумывая остроумную эвристику, решающую некоторую сложну задачу, стоит задуматься:, а можно ли сформулировать задачу так, чтобы компьютер мог самостоятельно перебрать миллионы эвристик и выбрать ту, которая решает поставленную задачу наилучшим образом.
Спасибо за внимание.
