Лень двигатель прогресса. Генератор задач. Часть 2
О том, как сделать свой генератор простых задач на нахождение пределов/производных/интегралов и пойдёт речь после ката.
P.s. Опыт создания похожей программы описан в предыдущей части
Как можно увидеть из картинки, задачи будем генерировать в pdf при помощи LaTex. О нем было уже много разных статей, так что вводную часть опущу. Реализовывать и создавать задачи будем через Pascal (но общий алгоритм опишу и спрячу весь код в спойлеры).
Приступим
Для начала нужно определить понятие полинома (многочлена), так как тригонометрические функции опираются именно на многочлен. В составе стандартных операций нужно ввести:
- Сложение многочленов
- Вычитание многочленов
- Перемножение многочленов
- Возведение в натуральную степень
- Перевод в текст Tex-а
- Производная
- Интеграл
st: integer;//степень многочлена
kof: array of real;//коэффициенты при x^i
function into (x: real): real;
class function operator+(a, b: polynomial): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength (rez.kof, stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if (i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if (i<=b.st)then
rez.kof[i]:=rez.kof[i]+b.kof[i];
end;
rez.st:=stn;
result:=rez;
end;
class function operator-(a, b: polynomial): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength (rez.kof, stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if (i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if (i<=b.st)then
rez.kof[i]:=rez.kof[i]-b.kof[i];
end;
while (rez.kof[stn]=0)do
begin
setlength (rez.kof, stn);
stn:=stn-1;
end;
rez.st:=stn;
result:=rez;
end;
class function operator*(a, b: polynomial): polynomial;
var i, j, stn: integer;
rez: polynomial;
begin
stn:=a.st+b.st;
setlength (rez.kof, stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to a.st do
for j:=0 to b.st do
begin
rez.kof[i+j]:=rez.kof[i+j]+a.kof[i]*b.kof[j];
end;
while (rez.kof[stn]=0)do
begin
setlength (rez.kof, stn);
stn:=stn-1;
end;
rez.st:=stn;
result:=rez;
end;
class function operator*(a: integer; b: polynomial): polynomial;
var i: integer;
begin
for i:=0 to b.st do
b.kof[i]:=a*b.kof[i];
result:=b;
end;
class function operator in (a: polynomial; n: integer): polynomial;
var i: integer;
rez: polynomial;
begin
rez.st:=0;
setlength (rez.kof,1);
rez.kof[0]:=1;
for i:=1 to n do
rez:=rez*a;
result:=rez;
end;
procedure nw (x: integer);
function pltostr: string;//в строковую переменную
procedure derivative;//производная
procedure integral;//интеграл
end;
procedure polynomial.nw (x: integer);
var
i: integer;
begin
st:=x;
setlength (kof, st+1);
for i:=0 to st do
kof[i]:=random (-10,10);
while (kof[st]=0)do
kof[st]:=random (-10,10);
end;
procedure polynomial.integral;
var
i: integer;
begin
setlength (kof, st+2);
for i:=st downto 1 do
kof[i+1]:=kof[i]/i;
kof[0]:=0;
st:=st+1;
setlength (kof, st+1);
end;
procedure polynomial.derivative;
var
i: integer;
begin
for i:=1 to st do
kof[i-1]:=kof[i]*i;
st:=st-1;
setlength (kof, st+1);
end;
Вслед за обычным многочленом потребуется ввести многочлен с корнями (чтобы можно было искать корни или сокращать дроби).
Но тут будет особенность, так как нужно сделать те же самые свойства не только для того же класса, но и для обычного многочлена.
st: integer;//степень многочлена
root: array of integer;//корни многочлена
kof: array of integer;//коэффициенты при x^i
class function operator+(a, b: polynomialwithroot): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength (rez.kof, stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if (i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if (i<=b.st)then
rez.kof[i]:=rez.kof[i]+b.kof[i];
end;
rez.st:=stn;
result:=rez;
end;
class function operator+(a: polynomialwithroot; b: polynomial): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength (rez.kof, stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if (i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if (i<=b.st)then
rez.kof[i]:=rez.kof[i]+b.kof[i];
end;
rez.st:=stn;
result:=rez;
end;
class function operator+(b: polynomial; a: polynomialwithroot): polynomial;
// var i: integer;
// rez: polynomial;
begin
result:=a+b;
end;
class function operator-(a, b: polynomialwithroot): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength (rez.kof, stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if (i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if (i<=b.st)then
rez.kof[i]:=rez.kof[i]-b.kof[i];
end;
while (rez.kof[stn]=0)do
begin
setlength (rez.kof, stn);
stn:=stn-1;
end;
rez.st:=stn;
result:=rez;
end;
class function operator-(a: polynomialwithroot; b: polynomial): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength (rez.kof, stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if (i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if (i<=b.st)then
rez.kof[i]:=rez.kof[i]-b.kof[i];
end;
while (rez.kof[stn]=0)do
begin
setlength (rez.kof, stn);
stn:=stn-1;
end;
rez.st:=stn;
result:=rez;
end;
class function operator-(b: polynomial; a: polynomialwithroot): polynomial;
var i, stn: integer;
rez: polynomial;
begin
if (a.st>b.st)then stn:=a.st
else stn:=b.st;
setlength (rez.kof, stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to stn do
begin
if (i<=a.st)then
rez.kof[i]:=rez.kof[i]+a.kof[i];
if (i<=b.st)then
rez.kof[i]:=rez.kof[i]-b.kof[i];
end;
while (rez.kof[stn]=0)do
begin
setlength (rez.kof, stn);
stn:=stn-1;
end;
rez.st:=stn;
result:=rez;
end;
class function operator*(a, b: polynomialwithroot): polynomialwithroot;
var i, j, stn: integer;
rez: polynomialwithroot;
begin
stn:=a.st+b.st;
setlength (rez.kof, stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to a.st do
for j:=0 to b.st do
begin
rez.kof[i+j]:=rez.kof[i+j]+a.kof[i]*b.kof[j];
end;
while (rez.kof[stn]=0)do
begin
setlength (rez.kof, stn);
stn:=stn-1;
end;
rez.st:=stn;
setlength (rez.root, rez.st);
for i:=0 to a.st-1 do
rez.root[i]:=a.root[i];
for i:=0 to b.st-1 do
rez.root[a.st+i]:=b.root[i];
result:=rez;
end;
class function operator*(a: polynomialwithroot; b: polynomial): polynomial;
var i, j, stn: integer;
rez: polynomial;
begin
stn:=a.st+b.st;
setlength (rez.kof, stn+1);
for i:=0 to stn do
rez.kof[i]:=0;
for i:=0 to a.st do
for j:=0 to b.st do
begin
rez.kof[i+j]:=rez.kof[i+j]+a.kof[i]*b.kof[j];
end;
while (rez.kof[stn]=0)do
begin
setlength (rez.kof, stn);
stn:=stn-1;
end;
rez.st:=stn;
result:=rez;
end;
class function operator*(b: polynomial; a: polynomialwithroot): polynomial;
// var i, j, stn: integer;
// rez: polynomial;
begin
result:=a*b;
end;
class function operator in (a: polynomialwithroot; n: integer): polynomialwithroot;
var i: integer;
rez: polynomialwithroot;
begin
rez:=a;
for i:=2 to n do
rez:=rez*a;
result:=rez;
end;
procedure nw;
procedure roots (x: integer);
function pltostr: string;
end;
procedure polynomialwithroot.roots (x: integer);
var i: integer;
begin
st:=x;
setlength (root, st);
for i:=0 to st-1 do
begin
root[i]:=random (-5,5);
end;
nw;
end;
procedure polynomialwithroot.nw;
var
i, j, sum: integer;
tk: array of integer;
dop: integer;
begin
setlength (kof, st+1);
setlength (tk, st+1);
for i:=0 to st-1 do
kof[i]:=0;
for i:=0 to st-1 do
begin
for j:=0 to st do
tk[j]:=0;
while (tk[st]=0)do
begin
sum:=0;
for j:=0 to st-1 do
sum:=sum+tk[j];
if (sum=(i+1))then
begin
dop:=1;
for j:=0 to st-1 do
if (tk[j]=1)then
dop:=dop*root[j];
for j:=0 to i do
dop:=-dop;
kof[st-i-1]:=kof[st-i-1]+dop;
end;
tk[0]:=tk[0]+1;
for j:=0 to st-1 do
begin
tk[j+1]:=tk[j+1]+(tk[j] div 2);
tk[j]:=tk[j] mod 2;
end;
end;
end;
kof[st]:=1;
end;
А дальше по однотипному примеру работаем с тригонометрическими функциями (включая логарифм и e^x).
x: polynomial;
s: string;
procedure nw;
procedure derivative;//производная
end;
type cosx= record
x: polynomial;
s: string;
procedure nw;
procedure derivative;//производная
end;
type tgx= record
x: polynomial;
s: string;
procedure nw;
procedure derivative;//производная
end;
type ctgx= record
x: polynomial;
s: string;
procedure nw;
procedure derivative;//производная
end;
type lnx=record
s: string;
x: polynomial;
procedure nw;
procedure derivative;
end;
type ex=record
s: string;
f, x: polynomial;
procedure nw;
procedure derivative;
end;
Заранее оговорюсь, что не буду использовать никаких тригонометрических формул дальше. Это увеличит сложность не только для решения, но и для составления схем задач.
Немного о TeX
Для упрощения работы с TeX был создан отдельный класс, чтобы потом вынести все в отдельный модуль.
Класс отвечает за:
- Создание нового tex файла (создание и вводный блок)
- Построчного добавления текста (в конце строки будет переход на новую строку)
- Создание нового tex файла
- Закрытия tex файла (закрывающий блок и прекращение работы с файлом)
- Создание pdf через установленный на компьютер Tex
- Открытие pdf файла
namefl: string;
procedure newtex (s: string);
procedure add (s: string);
procedure closetex;
procedure createpdf;
procedure openpdf;
end;
implementation
procedure tex.newtex (s: string);
var
t: text;
begin
namefl:=s;
assign (t, s+'.tex');
rewrite (t);
writeln (t,'\documentclass[12pt]{article}');
writeln (t,'\usepackage{amsmath}');
writeln (t,'%\usepackage[rus]{babel}');
writeln (t,'%\usepackage[cp1251]{inputenc}');
writeln (t,'\begin{document}');
close (t);
end;
procedure tex.add (s: string);
var
t: text;
begin
assign (t, namefl+'.tex');
append (t);
writeln (t,'\[');
writeln (t, s);
writeln (t,'\]');
close (t);
end;
procedure tex.closetex;
var
t: text;
begin
assign (t, namefl+'.tex');
append (t);
writeln (t,'\end{document}');
close (t);
end;
procedure tex.createpdf;
var
p: System.Diagnostics.Process;
begin
p:=new System.Diagnostics.Process ();
p.StartInfo.FileName:='pdflatex';
p.StartInfo.Arguments:=namefl+'.tex';
p.Start ();
end;
procedure tex.openpdf;
var
p: System.Diagnostics.Process;
begin
p:=new System.Diagnostics.Process ();
p.StartInfo.FileName:=namefl+'.pdf';
p.Start ();
end;
Схема задач
Заранее оговорюсь, что задача на производную и интеграл обратные, так что нужна только одна схема на две задачи.
Пределы
В начале курса математического анализа чаще всего всплывают пределы (при x→ inf): inf/inf, 0/0, inf-inf, a/inf и a/b.
Значит и схемы таких задач должны проверять на вшивость понимание разницы.
1. Пример, где ответ нуль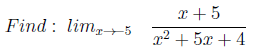
Задание строится по типу P1(x)/P2(x)* при х стремящимся к корню P1(x) (и не является корнем P2(x)).
*P1(x) и P2(x) многочлены с корнями от 1 до 3 (иногда 4-ой) степени (рандомная генерация)
2. Нуль в знаменателе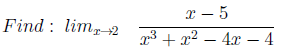
Достаточно просто. По аналогии с первым примером, тут нуль в знаменателе.3. Нули в числителе и знаменателе
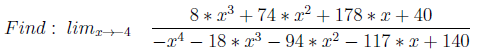
Строятся два многочлена с корнями так, чтобы один корень был у обоих P (x). Тогда при x стремящемся к этому корню будет отношение 0/0. Отсюда необходимость дифференцировать P1(x) и P2(x), чтобы найти правильный ответ.4. Бесконечность минус бесконечность
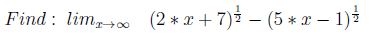
Пример по принципы inf-inf я решил демонстрировать на примере корней (часто встречалось в книжках, но есть и другие примеры).
Тут в основе лежит то, что P3(x)* и P4(x)* одной степени, а решение состоит в том, чтобы домножить и поделить на сопряженное.
*P3(x), P4(x) — многочлены под корнем первой степени
Производные и интегралы
«Берешь и считаешь»

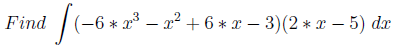
Примеры строятся следующим образом: берется производная функции (многочлен/тригонометрическая функция) и нужно найти её интеграл (по сути первоначально взятую функцию).Метод хитрого взгляда
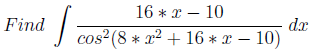
Задачу можно строить различными способами. Один из них взять тригонометрическую функцию T (P (x)) (P (x) многочлен второй или более высокой степени) и перемножить T (P (x)) на производную P (x). Такой прием нужно уметь замечать, чтобы не использовать разложение интеграла.
interface
uses mathUnit;
type taskderivative=record
task: string;
answer: string;
end;
type tasklimits=record
task: string;
answer: string;
end;
function taskintegral1(var s: string): string;
function tasklimits1(var s: string): string;
function tasklimits2(var s: string): string;
function tasklimits3(var s: string): string;
function tasklimits4(var s: string): string;
function taskderivative1(var s: string): string;
function taskderivative2(var s: string): string;
procedure rand (var x: taskderivative);
procedure rand (var x: tasklimits);
implementation
function correct (s: string): string;
var i: integer;
begin
for i:=1 to length (s) do
case s[i] of
'{': s[i]:='(';
'}': s[i]:=')';
end;
result:=s;
end;
function tasklimits1(var s: string): string;
var
p1, p2: polynomialwithroot;
i: integer;
x: integer;
rez: string;
k1, k2, r1, r2: integer;
begin
randomize;
p1.roots (random (1,3));
p2.roots (random (1,3));
i:=random (p1.st)-1;
for i:=i downto 0 do
p2.root[random (p2.st)]:=p1.root[random (p1.st)];
i:=random (p1.st)+random (p2.st);
if (i>p1.st-1)then
begin
x:=p2.root[i-(p1.st-1)];
end
else
x:=p1.root[i];
p1.nw;
p2.nw;
rez:='Find:\; lim_{x\to\!'+inttostr (x)+'}\quad \frac{'+p1.pltostr+'}{'+p2.pltostr+'}';
k1:=0;
k2:=0;
r1:=1;
r2:=1;
s:='При\; сокращении\;(x-'+inttostr (x)+')\; получается\;';
for i:=0 to p1.st-1 do
if (p1.kof[i]=x)then
inc (k1)
else
r1:=r1*(x-p1.kof[i]);
for i:=0 to p2.st-1 do
if (p2.kof[i]=x)then
inc (k2)
else
r2:=r2*(x-p2.kof[i]);
if (k1>k2)then
s:='0';// s:=s+'нуль';
if (k2>k1)then
s:='inf';//s:=s+'нуль\; в\; знаменателе\; и\; получается\; бесконечность';
if (k1=k2)then
s:=inttostr (r1)+'/'+inttostr (r2);//s:=s+'число\;'+floattostr (r1/r2);
s:=correct (s);
result:=rez;
end;
function tasklimits2(var s: string): string;
var
f: polynomialwithroot;
g, x: polynomial;
st: integer;
rez, answ: string;
begin
f.roots (random (1,2));
g.nw (random (1,2));
x.nw (random (1,2));
st:=f.root[random (0, f.st-1)];
rez:='Find:\; lim_{x\to\!'+inttostr (st)+'}\quad \frac{'+(f*g).pltostr+'}{'+(f*x).pltostr+'}';
s:=floattostr (g.into (st))+'/'+floattostr (x.into (st));
s:=correct (s);
result:=rez;
end;
function tasklimits3(var s: string): string;
var
f, g: sqrnpolynomial;
x: polynomial;
rez, answ: string;
begin
f.nw (random (1,4),2);
g.nw (f.x.st,2);
x:=f.x-g.x;
rez:='Find:\; lim_{x\to\infty}\quad '+f.s+'-'+g.s;
if (x.st+1=f.x.st)then
s:=floattostr (x.kof[x.st])+'/'+floattostr (g.x.kof[g.x.st]+f.x.kof[g.x.st])
else
s:='0';
s:=correct (s);
result:=rez;
end;
function tasklimits4(var s: string): string;
var
f, g: polynomialwithroot;
kf1, kf2: polynomial;
a, i, j, num: integer;
rez, add: string;
begin
f.roots (random (1,2));
g.roots (random ((f.st),3));
num:=random (1, f.st-1);
for i:=0 to num-1 do
g.root[i]:=f.root[i];
g.nw;
// writeln (num);
sleep (1000);
num:=0;
for i:=0 to f.st-1 do
for j:=0 to g.st-1 do
if (f.kof[i]=g.kof[j])then num+=1;
// writeln (num);
// sleep (1000);
kf1.nw (random (1,2));
kf2.nw (0);
a:=random (2,5);
add:='\frac{'+(kf1+kf2).pltostr+'}{'+kf1.pltostr+'}';
for i:=1 to length (s) do
if (add[i]='x')then add[i]:='n';
rez:='Find \; x,\; when: \; lim_{n\to\infty}\quad '+
add+'\frac{('+f.pltostr+')^{n^'+inttostr (a)+'}}{('+g.pltostr+')^{n^'+inttostr (a)+'}}=e^{'+floattostr (kf2.kof[0])+'}';
s:=inttostr (num);
result:=rez;
end;
function taskintegral1(var s: string): string;
var
tr1: sinx;
tr2: cosx;
tr3: tgx;
tr4: ctgx;
f, g: polynomial;
r: integer;
rez: string;
begin
rez:='Find\;\int ';
r:=random (1,5);
case r of
1: begin
tr1.x.nw (random (1,3));
tr1.nw;
s:=tr1.s;
tr1.derivative;
rez:=rez+tr1.s+'\; dx';
end;
2: begin
tr2.x.nw (random (1,3));
tr2.nw;
s:=tr2.s;
tr2.derivative;
rez:=rez+tr2.s+'\; dx';
end;
3: begin
tr3.x.nw (random (1,3));
tr3.nw;
s:=tr3.s;
tr3.derivative;
rez:=rez+tr3.s+'\; dx';
end;
4: begin
tr4.x.nw (random (1,3));
tr4.nw;
s:=tr4.s;
tr4.derivative;
rez:=rez+tr4.s+'\; dx';
end;
5: begin
r:=random (1,2);
f.nw (random (1,3));
rez:=rez+'('+f.pltostr+')';
while (r<>0)do
begin
g.nw (random (1,3));
f:=f*g;
rez:=rez+'('+g.pltostr+')';
r:=r-1;
end;
f.integral;
s:=correct (f.pltostr);
rez:=rez+'\; dx';
end;
end;
s:=correct (s);
result:=rez;
end;
function taskderivative1(var s: string): string;
var
sinx1, sinx2: sinx;
cosx1, cosx2: cosx;
tgx1, tgx2: tgx;
ctgx1, ctgx2: ctgx;
f, g: polynomial;
r: integer;
rez: string;
bg, answ: string;
begin
randomize;
sinx1.x.nw (random (1,3));
sinx1.nw;
sinx2:=sinx1;
sinx2.derivative;
tgx1.x.nw (random (1,3));
tgx1.nw;
tgx2:=tgx1;
tgx2.derivative;
cosx1.x.nw (random (1,3));
cosx1.nw;
cosx2:=cosx1;
cosx2.derivative;
ctgx1.x.nw (random (1,3));
ctgx1.nw;
ctgx2:=ctgx1;
ctgx2.derivative;
r:=random (1,4);
case r of
1: begin
rez:=rez+sinx1.s;
answ:=sinx2.s;
end;
2: begin
rez:=rez+cosx1.s;
answ:=cosx2.s;
end;
3: begin
rez:=rez+tgx1.s;
answ:='('+tgx2.x.pltostr+')/(cos ('+tgx1.x.pltostr+')^2)';
end;
4: begin
rez:=rez+ctgx1.s;
answ:='('+(-1*ctgx2.x).pltostr+'))/(sin ('+ctgx1.x.pltostr+')^2)';
end;
end;
bg:=rez;
rez:='Find\; \frac{d}{dx}\;('+rez;
rez:=rez+')';
r:=random (1,2);
f.nw (random (1,3));
while (r>0)do
begin
g.nw (random (1,3));
rez:=rez+'(';
rez:=rez+g.pltostr;
rez:=rez+')';
f:=f*g;
r:=r-1;
end;
rez:=rez+')';
answ:='('+answ+')*('+g.pltostr+')+(';
g.derivative;
answ:=answ+bg+')*('+g.pltostr+')';
s:=answ;
s:=correct (s);
result:=rez;
end;
function taskderivative2(var s: string): string;
var
sinx1, sinx2: sinx;
cosx1, cosx2: cosx;
tgx1, tgx2: tgx;
ctgx1, ctgx2: ctgx;
f, g, st: polynomial;
r: integer;
rez: string;
answ, bg: string;
begin
randomize;
sinx1.x.nw (random (1,3));
sinx1.nw;
sinx2:=sinx1;
sinx2.derivative;
tgx1.x.nw (random (1,3));
tgx1.nw;
tgx2:=tgx1;
tgx2.derivative;
cosx1.x.nw (random (1,3));
cosx1.nw;
cosx2:=cosx1;
cosx2.derivative;
ctgx1.x.nw (random (1,3));
ctgx1.nw;
ctgx2:=ctgx1;
ctgx2.derivative;
r:=random (1,4);
case r of
1: begin
rez:=rez+sinx1.s;
answ:=sinx2.s;
end;
2: begin
rez:=rez+cosx1.s;
answ:=cosx2.s;
end;
3: begin
rez:=rez+tgx1.s;
answ:='('+tgx2.x.pltostr+')/(cos ('+tgx1.x.pltostr+')^2)';
end;
4: begin
rez:=rez+ctgx1.s;
answ:='('+(-1*ctgx2.x).pltostr+'))/(sin ('+ctgx1.x.pltostr+')^2)';
end;
end;
bg:=rez;
rez:='Find\; \frac{d}{dx}\;('+rez;
rez:=rez+')^{';
f.nw (random (1,3));
rez:=rez+f.pltostr+'}';
st:=f;
st.derivative;
answ:='(('+bg+')^{'+f.pltostr+'})*(('+st.pltostr+')*ln ('+bg+')+('+f.pltostr+')*('+answ+')/('+bg+')';
s:=answ;
s:=correct (s);
result:=rez;
end;
procedure rand (var x: taskderivative);
var
r: integer;
begin
randomize;
r:=random (1,2);
case r of
1: x.task:=taskderivative1(x.answer);
2: x.task:=taskderivative2(x.answer);
end;
end;
procedure rand (var x: tasklimits);
var
r: integer;
begin
randomize;
r:=random (1,4);
case r of
1: x.task:=tasklimits1(x.answer);
2: x.task:=tasklimits2(x.answer);
3: x.task:=tasklimits3(x.answer);
4: x.task:=tasklimits4(x.answer);
end;
end;
end.
Суммируя
Существует большое разнообразие типовых приемов и примеров, но для минимальной оценки понимания материала такой набор меня пару раз выручил. Разумеется этот набор можно расширять и расширять, но это дело каждого.
Ссылка на программу: GitHub
В том проекте есть и другие задачи, не описанные в этой статье по причине их неоднозначной работы (тестируются и обновляются).
Комментарии (5)
10 ноября 2016 в 18:43
0↑
↓
Это вам \cdot так отрисовало или вы действительно применяете звёздочку вместо него и \times?10 ноября 2016 в 18:48
0↑
↓
Если вы про сноски, то да, там звездочка. Пытался применить и \cdot и \times, но не получилось10 ноября 2016 в 18:57
0↑
↓
Я про иллюстрации в статье. Quicklatex.com неплохо справляется: http://quicklatex.com/cache3/e5/ql_2cb67d0875244ab2030c139df04b05e5_l3.pngОтветом же на вопрос «что, если не находишь нужных по уровню задач в книгах, которые есть под рукой?» будет либо составлять примеры вручную, либо искать другие книги, авторы которых не писали генератор однотипных заданий.
10 ноября 2016 в 19:10
0↑
↓
Ещё у Вас как-то странно $\to -5$ в пределе выглядит, конец стрелки сливается с минусом.Кажется, Wolfram Mathematica умеет хорошо генерировать задачи. Надо у OsipovRoman уточнить.
10 ноября 2016 в 22:02
0↑
↓
Вы научитесь вставлять в статью код, а также качественный LaTeX (Tex2Cms в помощь).
