Learn OpenGL. Урок 5.2 — Гамма-коррекция17.04.2018 10:33

Гамма-коррекция

Итак, мы вычислили цвета всех пикселей сцены, самое время отобразить их на мониторе. На заре цифровой обработки изображений большинство мониторов имели электронно-лучевые трубки (ЭЛТ). Этот тип мониторов имел физическую особенность: повышение входного напряжение в два раза не означало двукратного увеличения яркости. Зависимость между входным напряжением и яркостью выражалась степенной функцией, с показателем примерно 2.2, также известным как гамма монитора.

Эта особенность мониторов (по случайному совпадению) очень напоминает то, как люди воспринимают яркость: с подобной же (но обратной) степенной зависимостью. Чтобы лучше это понять, взгляните на следующее изображение:

Верхняя строка показывает как воспринимается яркость человеческим глазом: при увеличении яркости в 2 раза (например, от 0.1 до 0.2) картинка действительно выглядит так, будто она в два раза ярче: изменения видны довольно отчетливо. Однако, когда мы говорим о физической яркости света, как, например, о количестве фотонов, выходящих из источника света, верную картину дает нижняя шкала. На ней удвоение значения дает правильную с физической точки зрения яркость, но поскольку наши глаза более восприимчивы к изменениям темных цветов, это кажется несколько странным.

Поскольку для человеческого глаза более привычен верхний вариант, мониторы и по сей день используют степенную зависимость при выводе цветов, так что исходные, в физическом смысле, значения яркости преобразуются в нелинейные значения яркости, изображенные на верхней шкале. В основном это сделано потому, что так выглядит лучше.

Эта особенность мониторов действительно делает картинку лучше для наших глаз, но когда дело доходит до рендеринга графики появляется одна проблема: все параметры цвета и яркости, которые мы устанавливаем в наших приложениях, основаны на том, что мы видим на мониторе. А это означает что все эти параметры на самом деле являются нелинейными. Взгляните на график:

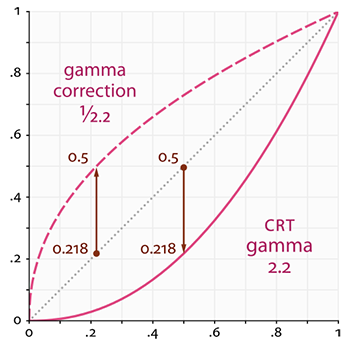
Серая линия соответствует значениям цвета в линейном пространстве; сплошная красная линия представляет собой цветовое пространство отображаемое монитором. Когда мы хотим получить в 2 раза более яркий цвет в линейном пространстве, мы просто берем и удваиваем его значение. Например, возьмем цветовой вектор $inline$\vec L = (0.5,0.0,0.0)$inline$, то есть темно-красный цвет. Если бы мы удвоили его значение в линейном пространстве, он стал бы равным $inline$(1.0,0.0,0.0)$inline$. С другой стороны, при выводе на дисплей, он будет преобразован в цветовое пространство монитора как $inline$(0.218, 0.0,0.0)$inline$, как видно из графика. Вот здесь и возникает проблема: удваивая темно-красный свет в линейном пространстве, мы фактически делаем его более чем в 4.5 раза ярче на мониторе!

До этого туториала мы предполагали, что работали в линейном пространстве, но на самом деле мы работали в цветовом пространстве, определяемом монитором, поэтому все установленные нами цвета и переменные освещения были физически не корректны, а всего лишь выглядели правильными конкретно на нашем мониторе. Руководствуясь данным предположением мы (и художники) обычно устанавливаем значения освещения ярче, чем они должны быть (т.к. монитор затемняет их), что в результате делает большинство последующих вычислений в линейном пространстве неверными. Также обратите внимание, что оба графика начинаются и заканчиваются в одних и тех же точках, затемнению на дисплее подвержены только промежуточные цвета.

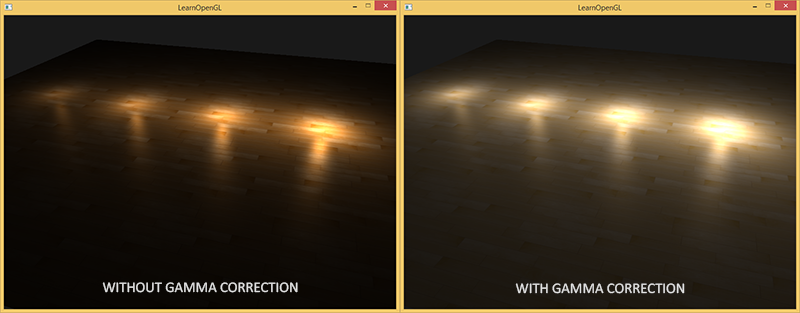
Как я уже говорил, поскольку значения цветов выбраны на основании отображаемой монитором картинки, все промежуточные вычисления освещения, проводимые в линейном пространстве физически некорректны. Это становится все очевиднее, когда мы начинаем использовать более продвинутые алгоритмы освещения. Просто взгляните на изображение:

Как видно, цветовые значения (которые мы предварительно обновили) с использованием гамма-коррекции куда лучше сочетаются между собой, а темные области становятся светлее, что увеличивает их детализацию. Налицо гораздо лучшее качество изображения, при весьма незначительных модификациях.

Без должным образом настроенной гаммы монитора освещение выглядит неправильно, и художникам будет довольно трудно получить реалистичные и красивые результаты. Чтобы решить эту проблему необходимо применять гамма-коррекцию.

Гамма-коррекция

Идея гамма-коррекции заключается в том, чтобы применить инверсию гаммы монитора к окончательному цвету перед выводом на монитор. Снова посмотрим на график гамма-кривой в начале этого урока, обратив внимание на еще одну линию, обозначенную штрихами, которая является обратной для гамма-кривой монитора. Мы умножаем выводимые значения цветов в линейном пространстве на эту обратную гамма-кривую (делаем их ярче), и как только они будут выведены на монитор, к ним применится гамма-кривая монитора, и результирующие цвета снова станут линейными. По сути мы делаем промежуточные цвета ярче, чтобы сбалансировать их затенение монитором.

Приведем еще один пример. Допустим, у нас опять есть темно-красный цвет $inline$(0.5,0.0,0.0)$inline$. Перед отображением этого цвета на монитор мы сперва применяем кривую гамма-коррекции к его компонентам. Значения цвета в линейном пространстве, при отображении на мониторе, возводятся в степень, приблизительно равную 2.2, поэтому инверсия требует от нас возведения значений в степень 1 / 2.2. Таким образом, темно-красный цвет с гамма-коррекцией становится $inline$(0.5,0.0,0.0)^{½.2}$inline$ = $inline$(0.5,0.0,0.0)^{0.45}$inline$ = $inline$(0.73,0.0,0.0)$inline$. Затем этот скорректированные цвет выводится на монитор, и в результате он отображается как $inline$(0.73,0.0,0.0)^{2.2}$inline$ = $inline$(0.5,0.0,0.0)$inline$. Как видите, когда мы используем гамма-коррекцию монитор отображает цвета, точно такими, какими мы задаем их в линейном пространстве в нашем приложении.

Гамма равная 2.2 это дефолтное значение, которое приблизительно выражает среднюю гамму большинства дисплеев. Цветовое пространство в результате применения этой гаммы называется цветовым пространством sRGB. Каждый монитор имеет свои собственные гамма-кривые, но значение 2.2 дает хорошие результаты на большинстве мониторов. Из-за этих небольших отличий многие игры позволяют игрокам изменять настройку гаммы.

Существует два способа применения гамма-коррекции к вашим сценам:

• Использовать встроенную в OpenGL поддержку sRGB для кадрового буфера.
• Выполнять гамма-коррекцию вручную, в фрагментных шейдерах.

Первый вариант проще, но дает вам меньше контроля. Установив флаг GL_FRAMEBUFFER_SRGB, вы сообщаете OpenGL, что каждая следующая за этим команда рисования должна выполнить гамма-коррекцию в цветовое пространство sRGB, прежде чем записать данные в цветовой буфер. После включения GL_FRAMEBUFFER_SRGB OpenGL автоматически выполнит гамма-коррекцию после запуска каждого фрагментного шейдера для всех последующих кадровых буферов, включая дефолтный кадровый буфер.

Включение флага GL_FRAMEBUFFER_SRGB выполняется при помощи обычного вызова glEnable:

glEnable(GL_FRAMEBUFFER_SRGB);

Теперь отрендеренные вами буферы цвета будут иметь скорректированную гамму и, поскольку это делается аппаратно это ничего нам не стоит. Единственное, о чем вы должны помнить при таком подходе (хотя и при другом подходе тоже), что гамма-коррекция преобразует цвета из линейного пространства в нелинейное, поэтому очень важно, чтобы вы выполняли гамма-коррекцию только на последнем, заключительном этапе. Если вы примените гамма-коррекцию до окончательного вывода, все последующие операции над этими цветами будут работать с неправильными значениями. Например, если вы используете несколько кадровых буферов, вы, вероятно, хотите, чтобы промежуточные результаты оставались в линейном пространстве и только последний буфер применял гамма-коррекцию перед отправкой на монитор.

Второй подход требует немного больше работы, но зато дает нам полный контроль над операциями с гаммой. Мы применяем гамма-коррекцию на соответствующем этапе фрагментного шейдера, так что к результирующим цветам применяется гамма-коррекция непосредственно перед отправкой на монитор:

void main()
{
    // делаем супер классное освещение
    [...]
    // применяем гамма-коррекцию
    float gamma = 2.2;
    FragColor.rgb = pow(fragColor.rgb, vec3(1.0/gamma));
}

Последняя строка кода возводит каждый компонент цвета fragColor в степень $inline$1.0 / gamma$inline$, корректируя результат работы данного шейдера.

Проблема этого подхода заключается в том, что вы должны применять гамма-коррекцию для каждого фрагментного шейдера, который вносит свой вклад в окончательный вывод, поэтому, если у вас есть дюжина фрагментных шейдеров для нескольких объектов, вам придется добавить код гамма-коррекции в каждый из них. Более разумным решением было бы добавить этап пост-обработки в ваш цикл рендеринга и применять гамма-коррекцию на финальном кваде в качестве последнего шага. Тогда вам нужно будет сделать это всего один раз.

Собственно, эти 2 строчки кода и представляют собой технические реализации гамма-коррекции. Не слишком впечатляет, правда? Подождите, есть еще пара нюансов, которые вы должны учитывать при гамма-коррекции.

sRGB текстуры

Всякий раз, когда вы рисуете или редактируете изображение на своем компьютере, вы выбираете цвета на основе того, что видите на мониторе. Фактически, это означает, что все созданные или редактируемые вами изображения находятся не в линейном пространстве, а в пространстве sRGB, то есть удвоение темно-красного цвета на экране, основанное на воспринимаемой вами яркости, на деле не равно удвоению красной составляющей цвета.

В результате, художники, рисующие текстуры, создают их в пространстве sRGB, и если мы используем эти текстуры в нашем приложении как они есть, мы должны учитывать это. До того как мы применили гамма-коррекцию это не создавало проблем, поскольку текстуры выглядели хорошо в пространстве sRGB, и без гамма-коррекции мы также работали в этом пространстве, так что текстуры отображались именно так, как задумано. Однако теперь, когда мы отображаем все в линейном пространстве, цвета текстуры передаются неверно, как видно на следующем изображении:

Текстура пересвечена, и это происходит потому, что гамма-коррекция, фактически, была применена к ней дважды! Посудите сами: когда мы создаем изображение на основе того, что видим на мониторе, мы корректируем гамму цветовых значений изображения, чтобы они выглядели верно на экране. Поскольку мы снова выполняем гамма-коррекцию при рендере, изображения становятся слишком яркими.

Чтобы решить эту проблему, мы должны убедиться, что художники, рисующие текстуры, работают в линейном пространстве. Однако, поскольку большинство художников даже не знают, что такое гамма-коррекция, и им проще работать в пространстве sRGB, это, скорее всего, не вариант.

Еще одно решение состоит в том, чтобы скорректировать или преобразовать эти sRGB-текстуры обратно в линейное пространство, прежде чем делать какие-либо манипуляции над их цветами. Мы можем сделать это следующим образом:

float gamma = 2.2;
vec3 diffuseColor = pow(texture(diffuse, texCoords).rgb, vec3(gamma));

Тем не менее проделывать это для каждой текстуры в пространстве sRGB довольно хлопотно. К счастью, OpenGL дает нам еще одно решение наших проблем, предоставляя нам внутренние форматы текстур GL_SRGB и GL_SRGB_ALPHA.

Если мы создадим текстуру в OpenGL с любым из указанных двух текстурных форматов sRGB, OpenGL автоматически преобразует их цвета в линейное пространство, как только мы их используем, что позволит нам правильно работать в линейном пространстве со всеми извлеченными из текстуры значениями цвета. Мы можем объявить текстуру как sRGB следующим образом:

glTexImage2D(GL_TEXTURE_2D, 0, GL_SRGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, image);

Если вы хотите использовать альфа-компонент в своей текстуре, вам нужно будет обозначить внутренний формат текстуры как GL_SRGB_ALPHA.

Вы должны быть осторожны при объявлении своих текстур как sRGB, поскольку не все текстуры будут находиться в пространстве sRGB. Текстуры, используемые для окраски объектов, такие как диффузные карты, почти всегда находятся в пространстве sRGB. Текстуры, используемые для извлечения параметров освещения, такие как бликовые карты и карты нормалей, наоборот, почти всегда находятся в линейном пространстве, поэтому, если вы объявите их как sRGB, освещение поедет. Будьте внимательны, при указании типов текстур.

Объявив наши диффузные текстуры как sRGB, вы снова получите ожидаемый результат, но на этот раз гамма-коррекцию достаточно применить всего 1 раз.

Затухание

Еще один момент, который будет иным при использовании гамма-коррекции — затухание освещения. В реальном физическом мире освещение затухает почти обратно пропорционально квадрату расстояния от источника света. На человеческом языке это означает, что сила света уменьшается при удалении от источника света, как показано ниже:

float attenuation = 1.0 / (distance * distance);

Однако при использовании этого уравнения эффект затухания слишком силен, и световое пятно получает небольшой радиус, что выглядит физически не слишком достоверно. Поэтому мы использовали другие уравнения для затухания (мы обсуждали это в туториале, посвященном основам освещения), которые дают больше возможностей настройки, или вообще линейный вариант:

float attenuation = 1.0 / distance;

Без гамма-коррекции линейный вариант дает гораздо более правдоподобные результаты, чем квадратичный, но когда мы включаем гамма-коррекцию, линейное затухание выглядит слишком слабым, и физически верное квадратичное неожиданно дает лучшие результаты. На рисунке ниже показаны различия между вариантами:

Причиной этого различия является то, что функции затухания света меняет яркость, и поскольку мы отображали нашу сцену не в линейном пространстве, мы выбрали функцию затухания, которая выглядела лучше всего на нашем мониторе, хоть и не была физически правильной. Когда мы использовали квадратичную функцию затухания без гамма-коррекции, фактически она превращалась в $inline$(1.0 / distance^2)^{2.2}$inline$ при отображении на мониторе, что давало гораздо больший эффект затухания. Это также объясняет, почему линейный вариант дает лучшие результаты без гамма-коррекции, ведь при нем $inline$(1.0 / distance)^{2.2}$inline$ = $inline$1.0 / distance^{2.2}$inline$, что намного больше напоминает физически правильную зависимость.

Более продвинутая функция затухания, которую мы обсуждали в основах освещения, по-прежнему полезна и в сценах с гамма-коррекцией, поскольку она дает гораздо больший контроль для более точной реализации затухания (но, конечно, требует других параметров при использовании гамма-коррекции).

Я написал простую демо сцену, исходный код которой вы можете найти здесь. Нажимая клавишу пробел, вы можете переключаться между сценами с гамма-коррекцией и без, каждая из которых использует свои текстуры и функции затухания. Это не самая впечатляющая демонстрация, но она показывает, как применять данные техники.

Подведем итоги: гамма-коррекция позволяет вам работать с цветами в линейном пространстве. Поскольку физическому миру присуще линейное пространство, большинство физических вычислений будут давать лучшие результаты, например расчет затухания света. Использование гамма-коррекции позволяет гораздо легче достигать реалистичных результатов по мере усложнения применяемых техник освещения. Именно поэтому рекомендуется сразу же настроить параметры освещения для работы с гамма-коррекцией.

Дополнительные материалы

• Что каждый разработчик должен знать о гамме — хорошо написанная, подробная статья Джона Новака (John Novak) о гамма-коррекции.
• www.cambridgeincolour.com — еще о гамме и гамма-коррекции.
• blog.wolfire.com — пост в блоге Дэвида Роузена (David Rosen) о преимуществах гамма-коррекции при рендере графики.
• renderwonk.com — еще некоторые практические соображения.

© Habrahabr.ru