Laplace Blur

Можно ли блюрить Лапласом вместо Гаусса, во сколько раз это быстрее, и стоит ли того потеря 1/32 точности.
(Laplace Blur — Предлагаемое оригинальное название алгоритма)
Сегодня мой внутренний демосценер пнул меня и заставил таки написать статью, которую нужно было написать уже полгода назад. Как любитель на досуге разрабатывать оригинальные алгоритмы эффектов, хотел бы предложить общественности алгоритм «почти гаусиан блюра», отличающийся применением исключительно быстрых процессорных инструкций (сдвигов и масок), а потому доступный к реализации вплоть до микроконтроллеров (чрезвычайно быстрый в ограниченном окружении).
По сложившейся у меня традиции написания статей на хабр, я буду приводить примеры на JS, как на языке максимально популярном, и хотите верьте хотите нет, очень удобном для целей быстрого прототипирования алгоритмов. К тому же, возможность реализовать это эффективно на JS пришла вместе с типизированными массивами. На моем не шибко мощном ноуте фулскрин изображение обрабатывается со скоростью 30fps (многопоточность воркеров задействована не была).
Сразу же скажу, что я перед вами снимаю шляпу, потому что сам считаю себя не достаточно подкованным в фундаментальной математике. Однако я всегда руководствуюсь общим духом фундаментального подхода. Поэтому перед тем как хейтить мой, в некоторой мере «наблюдательный» подход к аппроксимации, озаботьтесь подсчетом битовой сложности алгоритма, который, как вы думаете, может быть получен методами классической аппроксимации полиномами. Я угадал? Ими вы хотели быстро аппроксимировать? С учетом того, что они потребуют плавающей арифметики, они будут значительно медленнее, чем один битовый сдвиг, к которому я приведу пояснение в итоге. Одним словом, не торопитесь с теоретическим фундаментализмом, и не забывайте про контекст в котором я решаю задачу.
Данное описание присутствует здесь скорее для того, чтобы пояснить ход моих мыслей и догадок, которые привели меня к результату. Для тех кому будет интересно:
Оригинальная Функция Гаусса:
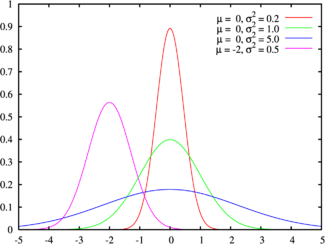
g (x) = a * e ** ( — ((x-b)**2) / c), где
а — амплитуда (если цвет у нас восемь бит на канал, то она = 256)
e — постоянная Эйлера ~2.7
b — сдвиг графика по х (нам не нужен = 0)
с — параметр влияющий на ширину графика связанный с ней как ~w/2.35
Наша частная функция (минус из показателя степени убран с заменой умножения делением):
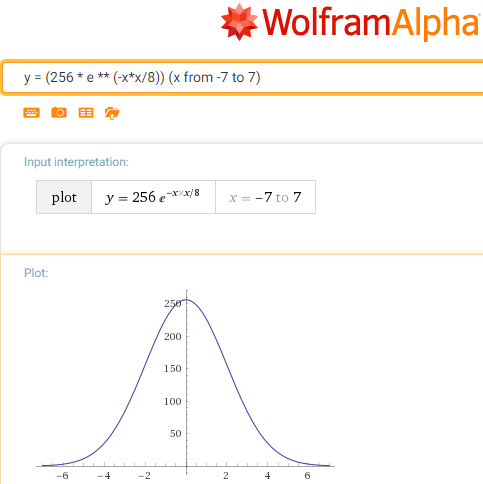
g (x) = 256 / e ** (x*x / c)
Да начнется грязное аппроксимационное действо:
Заметим, что параметр c — очень близок к полуширине и поставим 8 (это связано с тем, за сколько шагов можно сдвинуть по одному 8 бит канала).
Также грубо заменим e на 2, отметив однако, что это влияет больше на кривизну «колокола» нежели на его границы. На самом деле влияет в 2/e раз, но сюрприз в том, что эта ошибка компенсирует внесенную при определении параметра с, так что граничные условия у нас все еще в порядке, а погрешность появляется лишь в слегка некорректном «нормальном распределении», для графических алгоритмов это будет сказываться на динамике градиентных переходов цветов, но это почти невозможно заметить глазом.
Итак, теперь наша функция такова:
gg (x) = 256 / 2 ** (x*x / 8) или gg (x) = 2 ** (8 — x*x / 8)
Заметим, что показатель степени (x*x/8) имеет ту же область значения [0–8], что и функция меньшего порядка abs (x), потому последняя является кандидатом на замену. Быстро проверим догадку, глянув как меняется график при ней gg (x) = 256/ (2 ** abs (x)):
GaussBlur vs LaplasBlur:
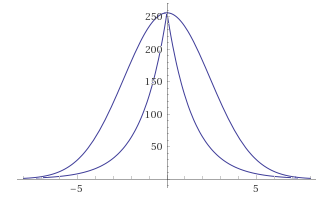
Кажется, отклонения слишком велики, к тому же функция, потеряв гладкость, теперь имеет пик. Но погодите.
Во первых, не будем забывать, что гладкость получаемых при размытии градиентов зависит не от функции плотности вероятности (коей является функция Гаусса), а от ее интеграла — функции распределения. На тот момент я этого факта не знал, но на самом деле, проведя «губительную» аппроксимацию относительно функции плотности вероятности (Гаусса), функция распределения при этом осталась достаточно похожей.
Было: 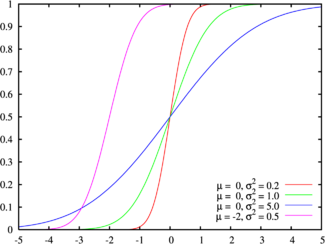
Стало: 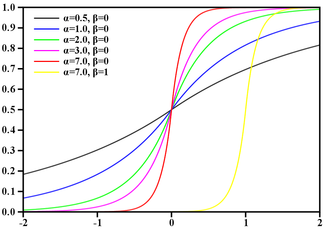
Пруф, снятый с готового алгоритма, совпадает: 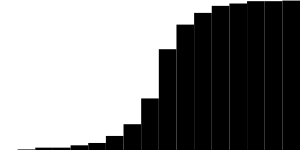
(забегая вперед скажу, что ошибка размытия моего алгоритма относительно Gausian x5 составила всего 3%)
Итак, мы перешли гораздо ближе к функции распределения Лапласа. Кто бы мог подумать, но им можно мыть изображения на 97% не хуже.
Пруф, разницы гаусиан блюра х5 и «Лаплас блюра» х7:

(это не черное изображение! Можете поизучать в редакторе)
Допущение этого преобразования позволило перейти к идее получения значения итеративной фильтрацией, к которому я планировал свести изначально.
Перед повествованием конкретного алгоритма будет честно, если я забегу вперед и сразу опишу его единственный недостаток (хотя реализацию можно исправить, с потерей скорости). Но данный алгоритм реализован с использованием сдвиговой арифметики, и степени 2ки являются его ограничением. Так оригинальный сделан для размытия х7 (что в тестах ближе всего соотноситься с Gausian x5). Связано это ограничение реализации с тем, что при восьмибитном цвете, сдвигая за шаг значение в накопителе фильтра на один бит, всякое воздействие от точки заканчивается максимум за 8 шагов. Я также реализовал чуть более медленную версию через пропорции и дополнительные сложения, которая реализует быстрое деление на 1.5 (получив в итоге радиус х15). Но с дальнейшим применением такого подхода погрешность растет, а скорость падает, что не позволяет его так использовать. С другой стороны, стоит заметить, что х15 уже достаточно, что бы не сильно замечать разницу, получен результат с оригинала или с даунсемплированого изоображения. Так что метод вполне годен, если нужна чрезвычайная скорость в ограниченном окружении.
Итак, ядро алгоритма простое, совершается четыре однотипных прохода:
1. Половина значения накопителя t (изначально равное нулю) складывается с половиной значения очередного пикселя, результат присваивается в него же. Продолжаем так до конца строки изображения. Для всех строк.
По завершению первого прохода изображение оказывается смазано в одну сторону.
2. Вторым проходом делаем то же самое в обратную сторону для всех линий.
Получаем изображение, полностью размытое по горизонтали.
3–4. Теперь делаем то же самое по вертикали.
Готово!
Изначально я использовал двухпроходный алгоритм с реализацией обратного размытия через стек, но он сложен для понимания, не грациозен, и к тому же на нынешних архитектурах оказался медленнее. Возможно, однопроходный алгоритм будет быстрее на микроконтроллерах, плюсом так же станет возможность выводить результат прогрессивно.
Текущий четырехпроходный способ реализации я подглядел на хабре у предыдущего гуру по алгоритмам размытия. habr.com/post/151157 Пользуясь случаем, выражаю ему свою солидарность и глубокую благодарность.
Но на этом хаки не закончились. Теперь по поводу того, как вычислять все три канала цвета за одну инструкцию процессора! Дело в том, что использованный в качестве деления на два битовый сдвиг позволяет очень хорошо контролировать позиции бит результата. Единственной проблемой становится то, что младшие разряды каналов сползают в соседние старшие, но можно просто обнулить их, чем исправить проблему, с некоторой потерей точности. А согласно описанной формуле фильтра, сложение половины значения накопителя с половиной значения очередной ячейки (при условии обнуления съехавших разрядов) никогда не приводит к переполнению, так что беспокоиться за него не стоит. И формула фильтра для одновременного вычисления всех разрядов становиться такой:
buf32[i] = t = (((t >> 1) & 0×7F7F7F) + ((buf32[i] >> 1) & 0×7F7F7F);
Однако требуется еще одно дополнение: опытным путем было выяснено, что потеря точности в данной формуле слишком значительна, визуально ощутимо прыгает яркость картинки. Стало понятно, что теряемый бит нужно округлять до целого, а не отбрасывать. Простым способом сделать это в целочисленной арифметике является прибавление половины делителя перед делением. Делитель у нас двойка, значит прибавлять нужно единицу, во все разряды, — константу 0×010101. Но с любым сложением нужно опасаться получить переполнение. Так что мы не можем использовать такую коррекцию для вычисления половинного значения очередной ячейки. (Если там белый цвет, мы получим переполнение, потому ее мы корректировать не будем). Но оказалось, что основную ошибку вносило многократное деление накопителя, который мы как раз скорректировать можем. Потому что, на самом деле, даже с такой коррекцией, значение в накопителе не поднимется выше 254. Зато при сложении с 0×010101 переполнения гарантировано не будет. И формула фильтра с коррекцией приобретает вид:
buf32[i] = t = ((((0×010101 + t) >> 1) & 0×7F7F7F) + ((buf32[i] >> 1) & 0×7F7F7F);
На самом деле формула достаточно хорошо выполняет коррекцию, так что при многократном повторном применении данного алгоритма к изображению, артефакты начинают виднеться только на втором десятке проходов. (не факт что повторение гаусиан блюра не даст подобных артефактов).
Дополнительно, есть замечательное свойство, при множестве проходов. (Являющееся заслугой не моего алгоритма, а самой «нормальности» нормального распределения). Уже на втором проходе Лаплас блюра функция плотности вероятности (если я правильно все прикинул) будет выглядеть как-то так:
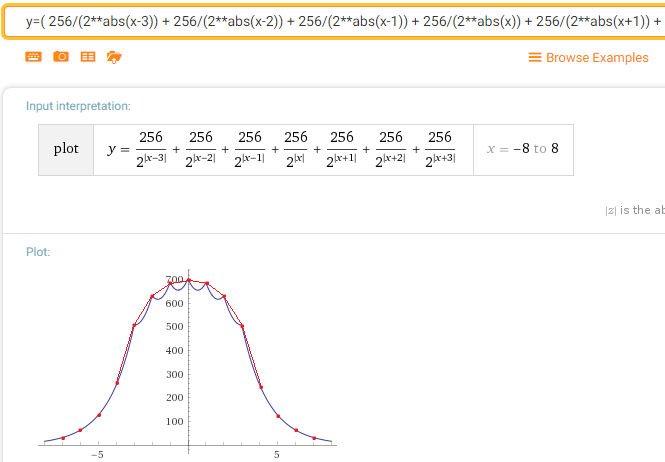
Что, согласитесь, уже очень близко к гаусиане.
Опытным путем я нашел, что использовать модификации с большим радиусом допустимо в паре, т.к. описанное выше свойство компенсирует ошибки, если последний проход является более точным (самый точный это описанный здесь алгоритм х7 блюра).
демо: impfromliga.github.io/LaplaceBlur
реп: github.com/impfromliga/LaplaceBlur
кодпен: codepen.io/impfromliga/pen/brXZjJ
Воззвание для крутых математиков:
Что было бы интересно узнать, насколько корректно использовать такой фильтр сепарабельно, не уверен получается ли там симметричная картина распределения. Хотя на глаз неоднородностей и не видно.
Предложения, комментарии, конструктивная критика — приветствуются!
