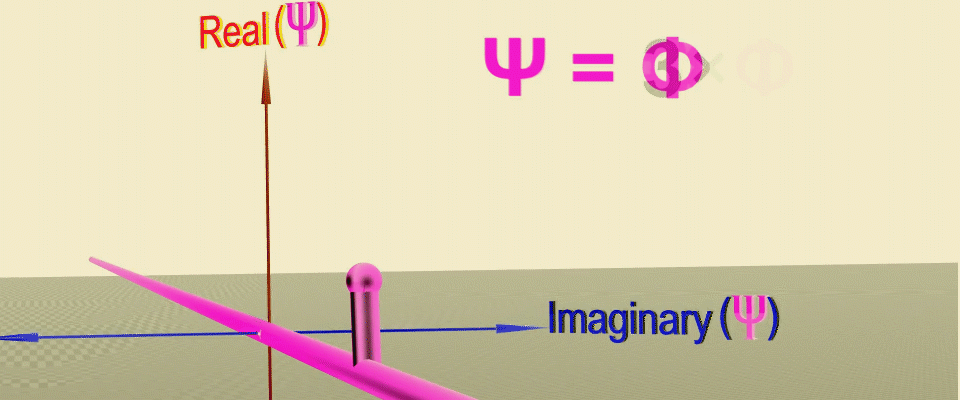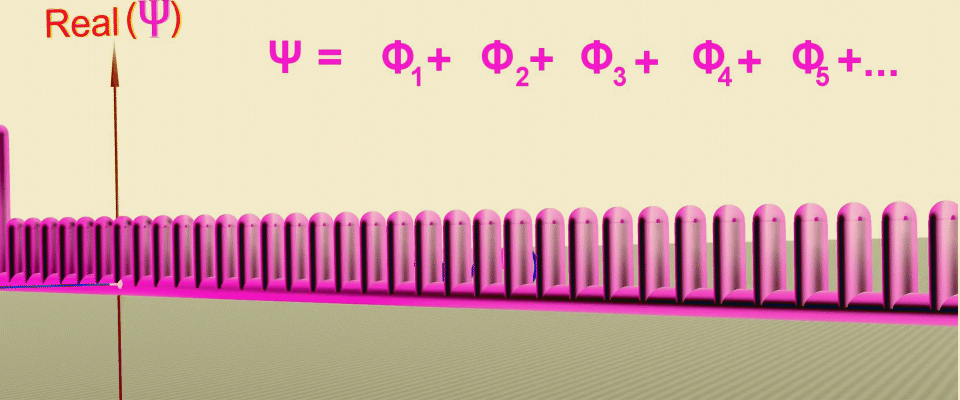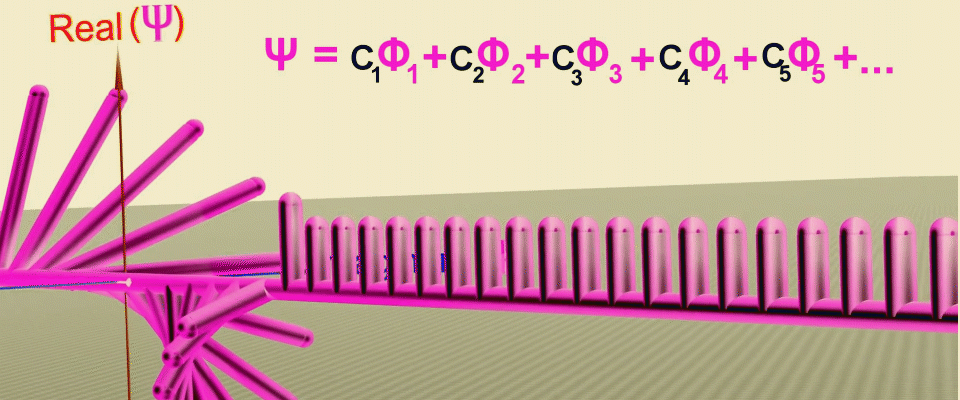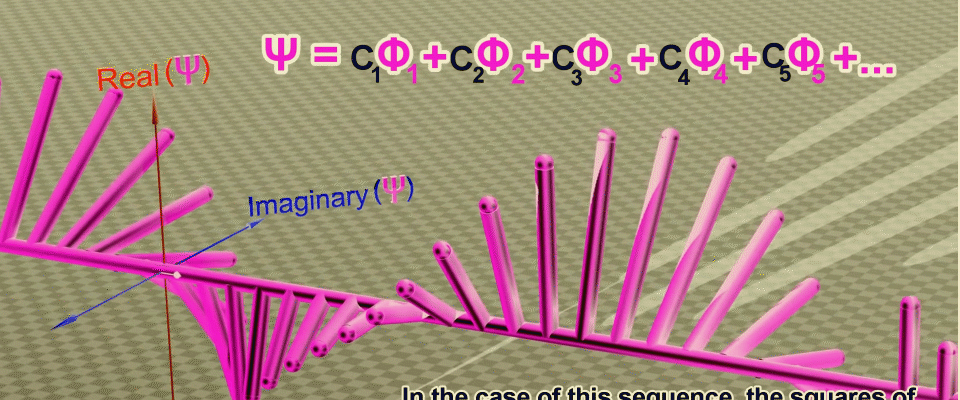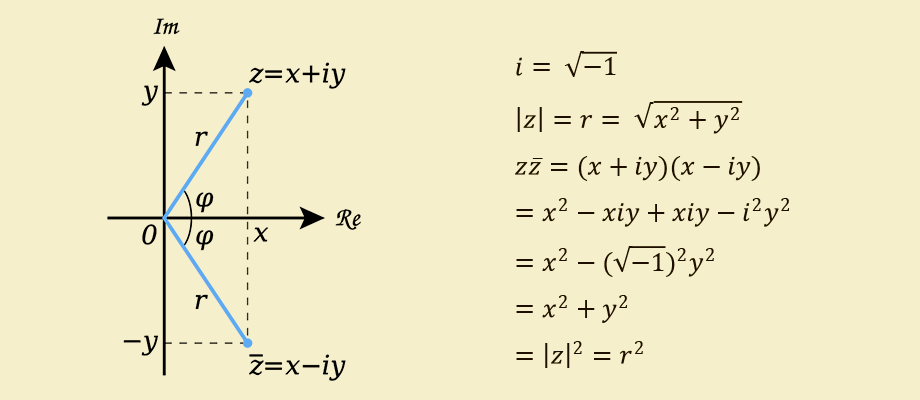Квантовая теория. Вселенная из волн вероятностей18.10.2020 10:03

Квантовая теория является одной из самых точных моделей, описывающих окружающий нас мир, а технические решения, разработанные благодаря применению аппарата квантовой механики, прочно вошли в повседневную жизнь современного общества. И тем удивительнее, что понимание даже базовых концепций этой сферы знаний вступает в серьезные противоречия с интуицией, не только людей далеких от науки, но и самих исследователей, подтверждением чему является большое количество различных интерпретаций. В этой статье, предлагаю рассмотреть основные понятия квантовой теории с показавшейся автору наиболее интуитивно-понятной точки зрения, несколько модифицированной теории вероятностей.

Что будет, если по аналогии с двущелевым опытом, все пространство на пути частицы до экрана будет заполнено щелями?

«Теория вероятности — единственный доступный математический инструмент, помогающий составить карту неизвестного и неконтролируемого.»
«Фрактальная геометрия природы» — Бенуа Мандельброт

Cодержание:

Введение: Демон Лапласа и Бог Эйнштейна
Принцип неопределенности, татуировка и каллиграфия
Волны материи и их амплитуды
Комплексные числа и фаза вероятности
Реальный мир и мнимые единицы
Волновая функция и плотность вероятности
Квантовый шлагбаум декогеренции
Немного квантовой криптографии
Заключение

Введение: Демон Лапласа или Бог Эйнштейна

В начале 19-го века, в научной картине мира доминировал детерминизм — учение о том, что начальные параметры системы полностью определяют её дальнейшее развитие. Ньютоновская механика, позволяла очень точно предсказывать поведение не слишком больших тел, двигающихся со скоростями намного меньшими скорости света, а появившиеся затем специальная и общая теория относительности сделали возможным подобные расчёты и для очень массивных объектов, двигающихся со скоростями близкими к скоростям света.

И только вопросом времени казалось создание демона Лапласа — гипотетического вычислительного устройства, которое будет способно получить на вход изначальные параметры любой системы и вычислить её стояние в любой момент. Ученые уже начали предвкушать практически полную победу над неопределенностью и торжество человеческого разума, хотя парадоксы, связанные с самой возможностью существования демона Лапласа, уже тогда вызывали большие сомнения.

Но примерно в тоже время попытки исследователей проникнуть в устройство природы на крайне малых пространственных и временных масштабах принесли плохие новости для детерминизма. Так, одно из основных утверждений новой квантовой теории — принцип неопределенности, гласил, что если у системы существуют связанные (коммутирующие) параметры, то, чем точнее мы измеряем один из них, то тем с меньшей определенностью мы можем определить другой.

Исходя из этих представлений, ни одно событие нельзя было предсказать с абсолютной точностью, поскольку в любых измерениях оставалась некоторая неточность и этот факт пришелся не по душе многим участникам научного сообщества того времени. Лагерь критиков возглавлял, уже имевший в то время мировой авторитет, Альберт Эйнштейн, который в переписке со своим оппонентом и коллегой Гейзенберга — Максом Борном, так отозвался о возможности существования принципа неопределенности:»… Во всяком случае, я убеждён, что [Бог] не играет в кости.»

Принцип неопределенности, татуировка и каллиграфия

Действие принципа неопределенности часто списывают на свойства самого процесса измерения, но есть и более фундаментальные причины и проще всего их продемонстрировать на примере двух параметров: импульса и координаты частицы. Подобно тому, как один и тот же рисунок можно выполнить двумя принципиально разными способами: векторным и растровым, то есть либо в виде линий, как, например, в каллиграфии, либо в виде набора точек, как в случае с татуировкой. Также и движение частицы можно описать двумя альтернативными способами: с помощью импульса — вектора массы-скорости $\vec p=m\vec v$ или с помощью набора пространственно-временных координат ${(x_1,t_1);(x_2,t_2);...;(x_n,t_n)}$ .

Слева: мастер каллиграфии рисует символ Энсо (яп. 円相,), источник. Справа: процесс нанесения татуировки на кожу человека, источник.

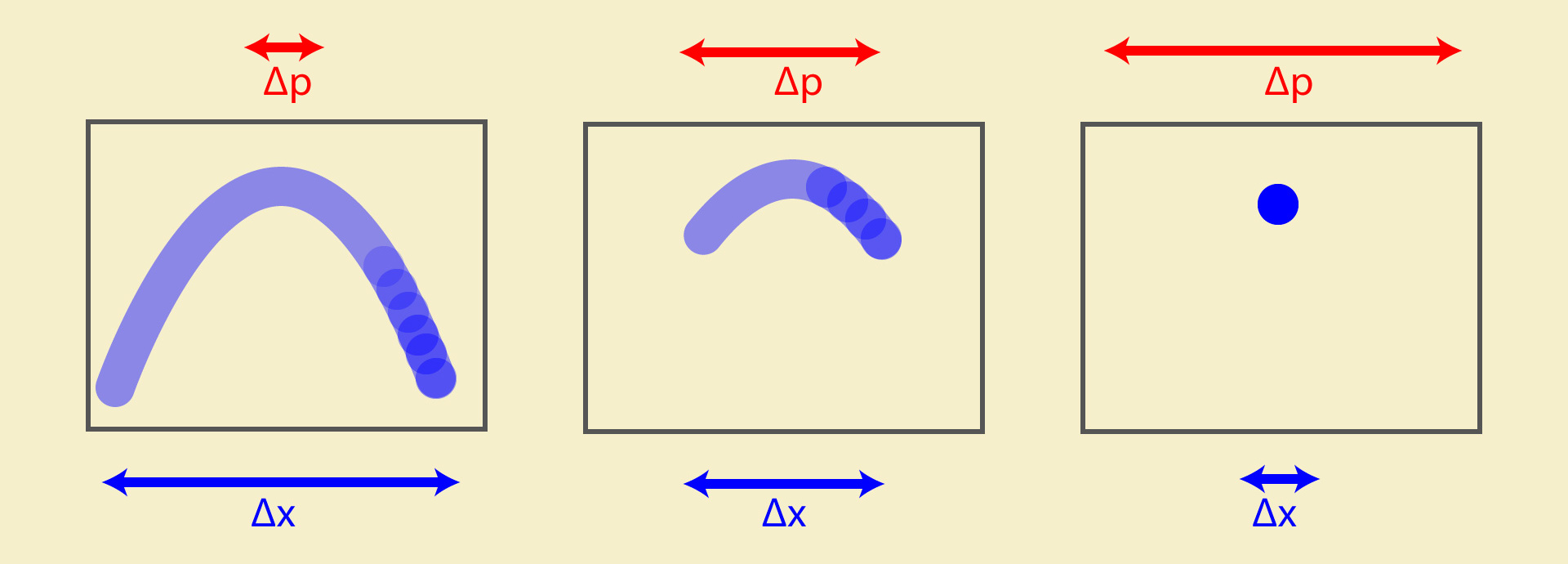
И согласно принципу неопределенности, чем точнее мы будем фиксировать координату объекта в пространстве-времени $Δx$ , тем меньше информации мы сможем получить о его импульсе. Представьте, что подброшенный вверх мячик, фотографируют несколько фотографов, у каждого на фотоаппарате стоит разная выдержка. Если выдержка большая, то на фотографии положение мяча получится смазанным, но зато будет хорошо виден вектор его движения. А чем меньше будет выдержка, тем чётче будет локализация объекта съемки и в пределе мы получим четкий подвешенный в воздухе мяч и совершенно ничего не сможем сказать о том, по какой траектории он двигался.

Три альтернативных снимка движущегося объекта, слева на право, показано как с увеличением пространственно-временного интервала (выдержки фотоаппарата), уменьшается количество информации об импульсе (траектории частицы).

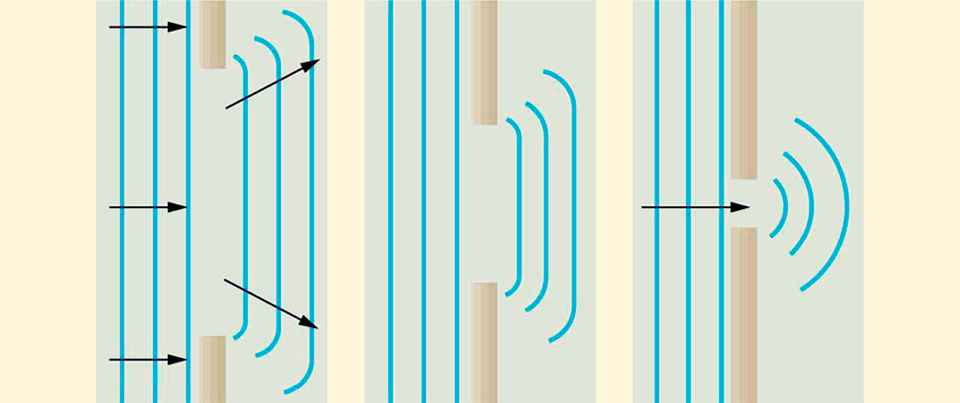
В мире макроскопических объектов, этот эффект не составляет большой проблемы, и если мы захотим задать координату автомобиля с точностью, сопоставимой с размерами самого автомобиля, то никаких проблем не будет — машина может спокойно заехать в тоннель и при этом сохранить свою предсказуемую траекторию. Но если мы попробуем проделать тоже самое, например, с фотонами и начнем пропускать их через уменьшающуюся щель, то сначала пятно света ожидаемо будет становится все более узким, но когда размер щели станет сопоставим с длиной волны фотона, то траектории фотонов на выходе из щели станут все менее предсказуемыми и световое пятно начнет расплываться в ширину. Иными словами, чем точнее мы будем знать где пролетела частица, тем меньше мы будем знать о том, куда она двинется дальше.

Вверху, слева на право: интерференционные картины получаемые при последовательном уменьшении щели, источник. Внизу: схема экспериментальной установки, источник.

Волны материи и их амплитуды

Но интерференцией луча света сложно кого-то удивить, ведь все и так знают, что свет — это волна, а каждая точка волнового фронта тоже будет являться источником волны и уменьшая щель мы, согласно принципу Гюйгенса — Френеля, получаем вторичный фронт, который с уменьшением размера щели все больше будет походить на волну от точечного источника.

Дифракция прямого волнового фронта, проходящего через отверстие, источник.

Действительно, любая волна по своей геометрической природе не локализуется в одной точке, ведь для создания даже у самой простой волны всегда будет два измерения — амплитуда и длина. И если мы начнем сжимать волну по высоте, то она будет расползаться в длину и наоборот. Но более интересно, что подобные эксперименты были поставлены и с частицами материи: электронами, атомами и даже с органическими молекулами и все они также демонстрировали волновую дифракцию.

Впервые идею о том, что не только фотоны, а вообще любая материя обладает волновыми свойствами высказал в 1923 году, французский физик Луи де Бройль в своей работе «Волны и кванты». Эта гипотеза была частично подтверждена уже в 1927 году, в результате опыта Дэвиссона-Гермера, который показал волновую дифракцию электронов, что принесло Луи де Бройлю заслуженную нобелевскую премию по физике в 1929 году.

Позднее с электронами был поставлен и известный двущелевой опыт который показал, что волны частиц материи могут не только испытывать дисперсию, образуя вторичные волновые фронты, но и эти вторичные волны могут усиливать друг друга, встречаясь в одной фазе или наоборот, взаимно гасится, встречаясь в противофазе, создавая интерференционную картину, подобно тому как ведут себя макроскопические волны на воде или акустические звуковые волны.

Слева: интерференция волн на воде, источник. Справа: интерференционная картина, полученная в результате регистрации одиночных электронов, проходящих через двойную щель источник.

Но если волны на воде — это колебательные движения частиц воды вверх и вниз, звуковые волны — это аналогичные движения молекул воздуха, то колебанием чего является волна материи, которая может быть фотоном, атомом, молекулой, человеком? Формально, ученые так и не пришли к единому мнению на этот счет, тем не менее научились вычислять функцию, которая эту волну описывает в зависимости от координаты или любого другого параметра, который можно измерить и обнаружили, что квадрат модуля этой функции являет собой точную оценку вероятности результатов измерения. Поэтому многие учёные, в числе которых был и выдающийся физик Ричард Фейнман, так и называли волновые функции — амплитудами вероятности. И это может показаться довольно странным, что вся материя и излучение являются волнами каких-то абстрактных математических понятий, но как мы постараемся показать далее, приняв это утверждение можно получить довольно понятное объяснение многих квантовых эффектов.

Комплексные числа и фаза вероятности

Из экспериментов с одной и двумя щелями мы уже знаем, что во многом амплитуды вероятностей ведут себя как самые обычные волны и даже могут, проходя через двойную щель накладываться друг на друга, усиливая или наоборот уменьшая вероятность появления частицы в точке, что создает интерференционную картину.

Демонстрация принципа интерференции волн. Слева: конструктивная интерференция — встреча пиков волн совпадающей фазе даёт более высокую результирующую амплитуду. Справа: деструктивная интерференция при встрече пиков волн в противоположной фазе. Источник.

И если мы определим вероятность события, как отношение количества исходов, приводящих к событию, к общему количеству всех возможных исходов, то получим, что вероятность — это положительное число, на отрезке от нуля до единицы, но тогда, если мы возьмем два любых графика плотности вероятности нахождения частицы в точке, то увидим, что сложение амплитуд этих графиков всегда будет больше, чем каждый из них по отдельности и никакой деструктивной интерференции не получится.

А что, если мы добавим волнам вероятности такое свойство, благодаря которому они смогут интерферировать? Представим прямую и каждая точка на ней будет соответствовать координате частицы, тогда от каждой точки перпендикулярно будем откладывать вероятность соответствующую нахождению частицы в этой точке. Соединив точку $x$ и соответствующую ей вероятность мы получим вектор — чем больше длина вектора, тем больше вероятность, нахождения частицы в этой точке, а чтобы эти векторы могли взаимодействовать, к длине еще добавим угол поворота и будем учитывать его при сложении.

Наверное, вы уже догадались что такая конструкция очень напоминает комплексные числа, которые так же имеют модуль — длину и фазу — угол. Тогда каждой координате будет соответствовать комплексная плоскость, в которой вектора вероятностей будут крутится как стрелки часов и если они будут смотреть в одном направлении, то они будут складываться, а если в противоположных, то наоборот вычитаться. Соединив концы этих стрелок, мы получим форму волновой функции или амплитуду вероятности для движения частицы по прямой в одном измерении.

Анимация последовательных преобразований, которые позволяют получить волновую функцию как сумму амплитуд вероятности в точках на пути частицы (зеленая линия), сначала задается вещественная часть амплитуды, а затем фаза (угол поворота) в комплексной плоскости. Источник.

Комплексные числа имеют вид $z=x+y*i$ , где первая часть — $x$ называется вещественной, а вторая — $y*i$ — мнимой. Эти две компоненты никогда не смешиваются, а в остальном подчиняются тем же правилам, что и обычные вещественные числа, с тем учётом, что $i$ — это мнимая единица и равна $\sqrt{-1}$ .

Одна из основных аксиом квантовой теории, под названием правило Борна, утверждает, что квадрат модуля волновой функции — даёт нам функцию плотности вероятности, то есть в нашем примере — распределение вероятностей нахождения частицы в зависимости от координаты.

Кратко освежим в памяти, модуль комплексного числа — это расстояние от начала координат — $(0, 0i)$ до точки с координатами $(x;yi)$ , то есть: $\sqrt{x^2+(y\sqrt{-1})^2}$ , видно, что $(\sqrt{-1})^2=1$ , но не будем пока списывать мнимую единицу, а найдем квадрат модуля:

$\left(\sqrt{x^2+(y\sqrt{-1})^2}\right)^2=x^2+(y\sqrt{-1})^2=(x+y\sqrt{-1})(x-y\sqrt{-1})$

Получаем, что квадрат модуля комплексного числа — это его произведение на такое же комплексное число, которое отличается только знаком перед коэффициентом мнимой части $z=x-y*i$ . Такие пары чисел называются комплексно сопряженными и представляют собой зеркальные отражения друг друга, соответствующие повороту векторов в комплексной плоскости на равные углы, но в противоположные стороны.

Где: $\overline z$ — комплексно сопряженное число

Реальный мир из мнимых единиц

Вот что мы уже поняли: волновая функция ставит в соответствие каждой координате некоторое комплексное число. Собственно, это и есть то чем занимаются волновые функции — ставят в соответствие какому-то измеряемому параметру комплексное число, угол поворота которого называется фазой. Фазы комлексных чисел отвечают за эффекты интерференции усиления и ослабления вероятностей, которые получаются путем умножения волновой функции на её же зеркальное отражение — комплексное сопряжение.

На вопрос почему квадрат модуля волновой функции даёт плотности вероятности, квантовая теория, обычно отвечает — заткнись и считай потому, что квадрат модуля делает из комплексного числа вещественное. Конечно такой ответ нас совершенно не устраивает, ведь из комплексного числа можно получить вещественное и просто взяв его модуль, поэтому хотелось бы понять смысл возведения модуля в квадрат.

Представим, что мы ничего не знаем ни о волновой функции, ни о функции плотности вероятности, а просто провели много наблюдений и отметили точками где и с какой частотой появляется частица. При этом мы понимаем, что получившееся распределение должно описываться каким-то графиком функции плотности вероятности и было бы крайне полезно узнать саму эту функцию.

Чтобы узнать какая функция соответствует нашим точкам, пойдем самым простым путём и начнем подгонять ответ под данные, то есть подбирать полиномы, которые будут проходить через максимальное количество имеющихся точек. Начнем с двух точек и подберём для них коэффициенты полинома первой степени, то есть линейной функции $y = ax + b$ ведь линия точно пройдет через наши две точки. Если остаются точки которые не лежат на этой прямой, то мы возьмем полином второго порядка $y = ax^2 + bx + c$ графиком которого являются различные параболы, подобрав коэффициенты мы гарантировано попадём, как минимум в три точки, одна из которых будет вершиной, а две других будут лежать на сторонах. Затем снова проверим остались ли еще точки лежащие вне графика если да — повторим увеличив степень полинома еще на единицу и так далее, логика понятна, полином степени $n$ гарантировано проходит через $n+1$ точек и в результате мы можем подобрать полином, который покроет все наши точки. Есть даже специальная теорема — апроксимационная теорема Вейерштрасса, которая подтверждает, что это возможно.

Пример подгонки точек, взятых из функции плотности вероятности нормального распределения, полиномами различной степени, от линейного, до полинома 18-й степени, с использованием функции numpy.polyfit. Можно убедится, что степень полинома соответствует количеству точек, через которые проходит его график.
Код Python:
from numpy import *
from matplotlib.pyplot import *
from mpl_toolkits.axes_grid.axislines import SubplotZero


mu, sigma = 0, 0.1
x = np.arange(-1,1,0.02)
y = 1/(sigma * np.sqrt(2 * np.pi))*np.exp( - (x - mu)**2 / (2 * sigma**2) )

y1 = poly1d(polyfit(x,y,1))	# linear
y2 = poly1d(polyfit(x,y,2))	# quadratic
y3 = poly1d(polyfit(x,y,3))	# cubic
y4 = poly1d(polyfit(x,y,4))	# 4th degree
y5 = poly1d(polyfit(x,y,10))	# 10th degree
y6 = poly1d(polyfit(x,y,18))	# 18th degree

fig = figure(figsize=(20,8), facecolor='#f4efcb', edgecolor='#f4efcb')
ax = SubplotZero(fig,111)
fig.add_subplot(ax)

ax.plot(x,y1(x),'r',label=u'линейный')
ax.plot(x,y2(x),'g',label=u'квадратичный')
ax.plot(x,y3(x),'orange',label=u'кубический')
ax.plot(x,y4(x),'b',label=u'$4$ степени')
ax.plot(x,y5(x),'c',label=u'$10$ степени')
ax.plot(x,y6(x),'m',label=u'$18$ степени')
ax.plot(x,y,'k.',label=u'данные')

ax.set_xlabel(u'x')
ax.set_ylabel(u'y')
ax.set_facecolor('#f4efcb')
ax.minorticks_on()
ax.legend(frameon=False,loc=8,labelspacing=.2)
ax.annotate('коэффициенты полинома 18 степени:'+'\n'+str(y6.coeffs), xy = (-1,1.2))

setp(ax.get_legend().get_texts(), fontsize='large')

fig.savefig("Curve fitting.svg",bbox_inches="tight",pad_inches=.15)

А раз плотность вероятности можно приблизить многочленом, то наверняка у этого многочлена есть и корни и еще одна замечательная теорема основная теорема алгебры говорит, что таки да — любой полином обязательно имеет решения в комплексных числах, а если корни вещественные, то это значит просто, что мнимая часть равна нулю (вектора будут иметь нулевой угол поворота), поскольку множество вещественных чисел полностью содержится во множестве комплексных $\mathbb{R} \subset \mathbb{C}$ .

И если любое комплексное число $z=x+y*i$ является корнем какого-либо полинома, то автоматически корнем этого же уравнения является и сопряженное ему число $\overline z=x-y*i$ , об этом нам говорит еще одна теорема — теорема о комплексно-сопряженных корнях.

Для примера представим, что плотность вероятности описывается полином второй степени $x^2+5*x+6,5$ и найдем его корни. По формуле корней квадратного уравнения $x_{1,2} = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$ , подставив коэффициенты $a=1, b=5, c=6,5$ и получим в виде решения два сопряженных комплексных числа $x_1=-5/2 + i/2$ , $x_2=-5/2 - i/2$ , как нам и утверждала теорема о сопряженных корнях.

С другой стороны, зная корни и воспользовавшись формулами Виета мы можем разложить тот же квадратный трехчлен следующим образом: $x^2+bx+c=(x-x_1)(x-x_2)$ легко проверить, что это верно, подставив полученные значения и раскрыв скобки мы получим исходный полином. Но в тоже время в правой части формулы Виета мы получили произведение двух сопряженных комплексных чисел, что есть квадрат модуля. В принципе эту же логику можно расширить и на остальные степени полиномов, главное, что всегда корни будут идти в паре, а для получения исходного полинома будет использоваться их перемножение.

Конечно это очень нестрогие рассуждения, призванные как-то осмыслить происходящее и на простом примере показать, что комплексные числа вполне обоснованы, а их сопряженные произведения могут давать что-то похожее на плотность вероятности.

Комикс с шуткой на тему действительных чисел (англ. real numbers) и умножения волновой функции на собственное комплексное сопряжение. Источник

Хорошо, будем считать, что у нас появилось некоторое представление о том, как устроены амплитуды вероятностей, почему они комплексные и как из них получаются обычные вероятности. И мы можем перейти к вопросу о том, что нам предсказывают эти вероятности, то есть о результатах измерений.

Волновая функция и плотность вероятности

Получая плотность вероятности нахождения частицы в определенной координате, мы предсказываем то, с какой частотой мы будем наблюдать частицу в разных точках. Например, если плотность вероятности будет описываться гауссовой кривой, как на левой части рисунка ниже, то в $68\%$ случаев мы увидим, что частица появится на отрезке от $-1\sigma$ до $+1\sigma$ , а в $95\%$ случаев на отрезке от $-2\sigma$ до $+2\sigma$ и так далее. Что в случае двумерного симметричного распределения, показанного справа, даст большую плотность обнаружения частицы в некотором круглом участке в центре и низкую плотность по мере удаления от центра:

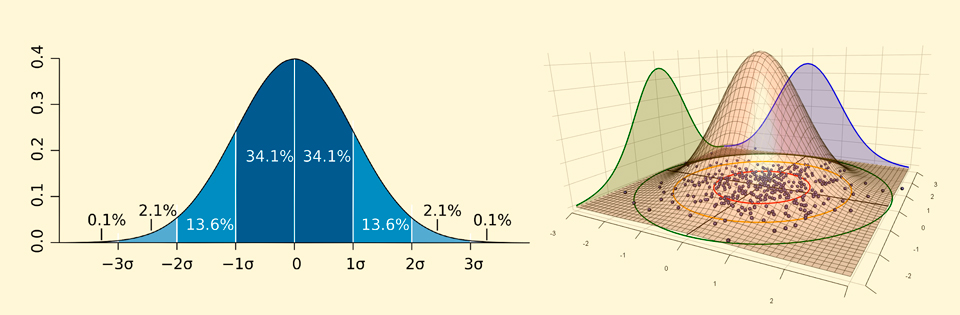
Довольно понятная схема: волновая функция от координаты задаёт форму распределения, которая затем говорит нам вероятности измерения частицы в точке пространства. Тем не менее такая интерпретация может приводить к странным противоречиям и иногда более естественно думать о частицах, как о волнах амплитуд вероятности. Например, на картинке ниже, слева показано, как выглядит плотность вероятности для электрона, находящегося во взаимодействии с ядром водорода. В соответствие с этим графиком можно получить форму, так называемых, электронных орбиталей — областей вокруг ядра атома, в которых взаимодействие с электроном наиболее вероятно, показанных справа:

Слева: кривые плотности вероятности нахождения электрона вокруг единичного протона, для трёх энергетических уровней . Справа: показан пример как выглядели бы распределения точек при проведении измерения координаты электрона. Источник.

На рисунке выше можно заметить, как меняются формы орбиталей в зависимости от энергетического уровня электрона — чем выше энергия электрона, тем, во первых, больше радиус оболочки, что вполне понятно, ведь чем больше энергия, тем сильнее электрон может сопротивляться притяжению ядра и тем дальше от ядра он может взаимодействовать, но вместе с этим, к каждому новому уровню энергии добавляется участок с нулевой вероятностью, называемый узлом (node), так, например, орбиталь электрона на 3 энергетическом уровне имеет форму слоеной сферы, содержащей внутри себя две зоны, вероятность обнаружения электрона в которых равна нулю.

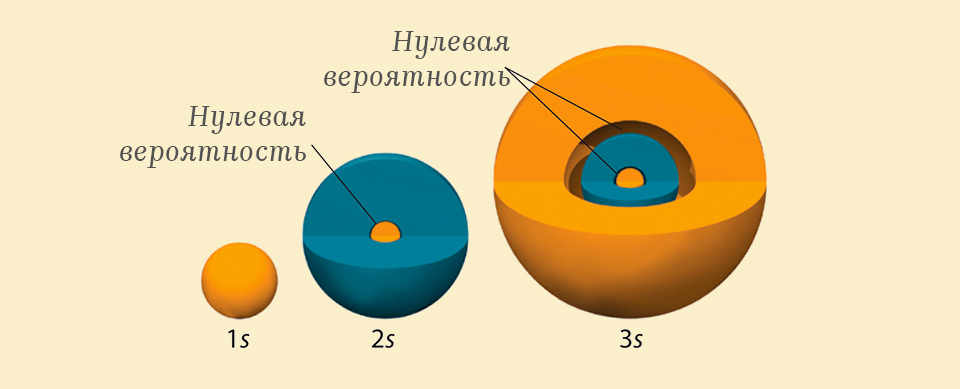
Контур вероятности нахождения электрона в окрестности ядра атома водорода для трех энергетических уровней слева на право: 1s, 2, s 3s. Источник.

Такое распределение вероятности выглядит очень странно, ведь попасть из одной сферы в другую, не пересекая вложенную между ними — невозможно.

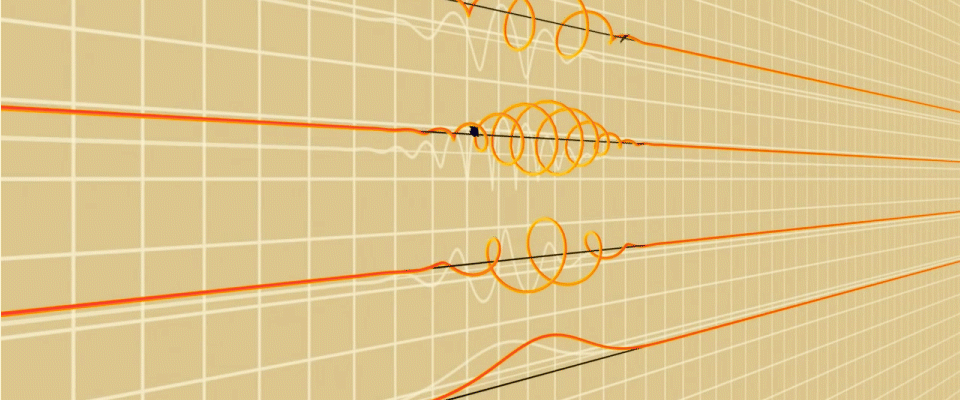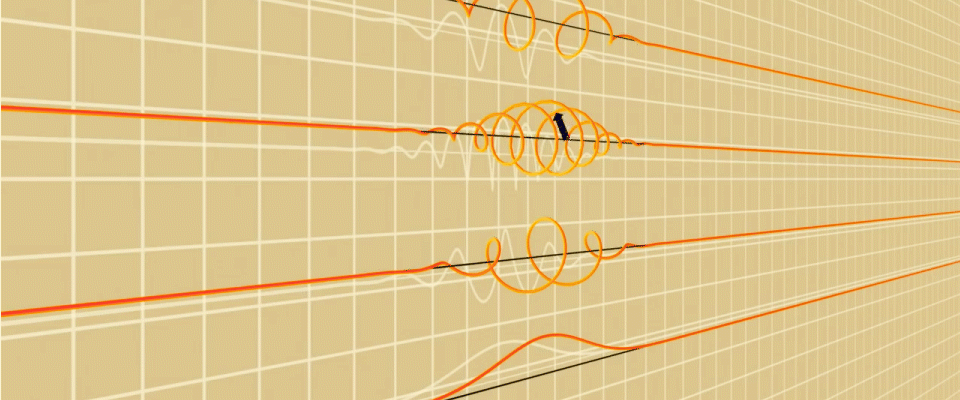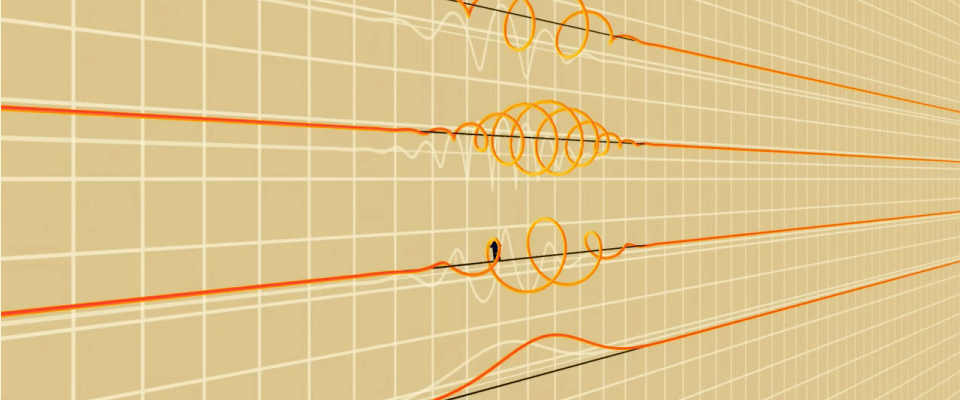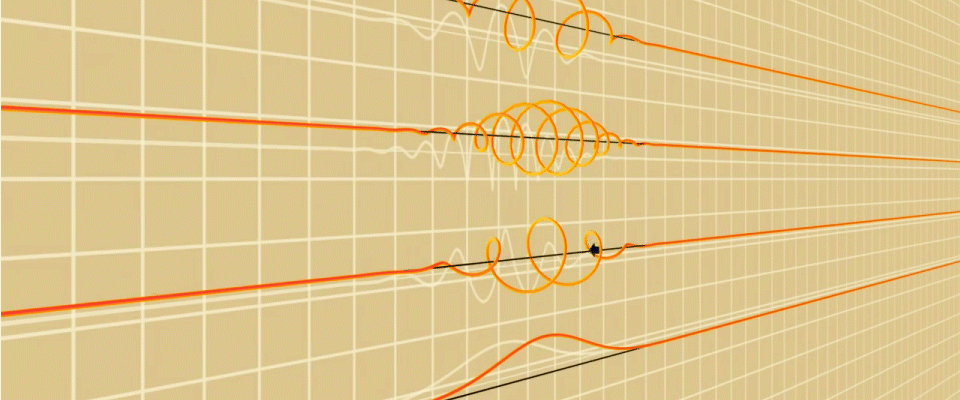
Но если думать об электроне, как об амплитуде вероятности, то все объясняется вполне естественно, на картинке ниже волновая функция от радиуса электрона вокруг ядра водорода, рассчитанная в одном измерении, для трех энергетических уровней.

Глядя на графики волновой функции легче понять, что электрон удерживаемый ядром атома представляет собой стоячую волну и как у любой стоячей волны, у неё будут появляться, так называемые, узлы (node) — зоны где амплитуда в результате интерференции с отраженной волной будет нулевой.

Пример образования узлов интерференции (красные точки) в одномерной стоячей волне, источник.

И если одномерная волна, как на анимации выше, всё еще не напоминает форму слоёной трёхмерной электронной оболочки атома водорода, то предлагаю представить волну на двумерной плоскости, распространяющуюся от точечного источника. Так, чтобы увидеть полную форму такой двумерной волны потребуется смотреть на неё в трех измерениях. А для жителя двумерного мира такая волна будет просто набором расходящихся от центра кругов. Аналогично и с трехмерными волнами — живут они в четырех измерениях, но для нас они будут выглядеть расходящимися трехмерными сферами.

Справа: анимация волны, распространяющейся по двумерной поверхности. Слева: пример того, как будет выглядеть проекция этой волны на плоскость.

Квантовый шлагбаум декогеренции

Авраам Паис (Abraham Pais) — выдающийся физик и историк науки, совместно работавший с целой плеядой из легенд науки 20 века, в числе которых: Джон фон Нейман, Альберт Эйнштейн, Нильс Бор, Макс Борн, Пол Дирак, Вольфганг Паули и многие другие, описывая один из диалогов, касающихся проблемы наблюдателя в квантовой физике, приводил вопрос, заданный ему Эйнштейном:

«Вы правда считаете, что Луна существует только тогда, когда вы на неё смотрите?» (Rev. Mod. Phys. 51, 863–914 (1979), p. 907).

И действительно древняя философская дилемма о существовании объективной реальности, с открытием квантовых свойств нашего мира стала еще актуальнее. Волновая функция даёт возможность с необходимой точностью предсказать результат измерения, но существует ли она в отрыве от контекста измерения и наблюдателя и как это проверить?

Прежде всего необходимо определить, что такое наблюдение и измерение. Чтобы измерить размер объекта, мы прикладываем к нему линейку, чтобы измерить температуру — прикладываем градусник, чтобы измерить скорость — отправляем на встречу электромагнитную волну.

Во всех этих случаях нам необходимо взаимодействие измеряемого объекта с каким-то другим объектом, состояние которого мы можем предварительно подготовить, такой объект назовем измерительной системой. Стряхнули градусник — подготовили измерительную систему, поставили подмышку — произвели взаимодействие, и затем оценили насколько изменилось состояние контрольной системы. Это общий принцип, любое измерение — это взаимодействие измеряемой системы с контрольной.

Любое наблюдение, также является измерением, наблюдая что-либо мы получаем информацию об объекте с помощью встроенных в наше тело измерительных систем, которые также взаимодействуют с объектом. Если мы смотрим на предмет — значит взаимодействуем с фотонами испущенными этим объектом, которые, попадая на сетчатку глаза, приводят к сложному каскаду взаимодействий и запуску нервного сигнала, поступающего в мозг.

«Тогда какова размерность клубка ниток? … С большого расстояния клубок представляет собой не более чем точку с нулевыми размерами. Приближаясь, можно увидеть, что это шар, который заполняет пространство в трех измерениях. Еще ближе можно увидеть саму нить, и объект становится фактически одномерным… Мандельброт без математики апеллировал к теории относительности: «Представление о том, что числовой результат должен зависеть от отношения объекта к наблюдателю, в духе физики нашего столетия и даже является образцовой её иллюстрацией».
«Хаос. Создание новой науки» — Джеймс Глейк

Принцип суперпозиции волн говорит нам, что когда две или более волн встречаются в одной точке пространства, то результатом взаимодействия будет новая волна, являющаяся суммой их амплитуд. Тогда, результатом измерения всегда будет всегда некоторая суперпозиция волновых функций измеряемой и измерительной системы.

Теперь возникает резонный вопрос: если мы примем утверждение о том, что все состоит из волн амплитуд вероятности, то почему мы так скучно живем не наблюдаем волновых свойств таких, как суперпозиция и интерференции у макроскопических объектов, окружающих нас?

Чтобы ответить на этот вопрос, снова взглянем на двухщелевой опыт: электроны по одному пролетают через двойную щель и попадая на экран, отмечаются на нем точкой, при многократном повторении этого процесса, точки образуют интерференционную картину, которая соответствует прохождению волны через две щели.

Слева: анимация интерференционной картины от прохождения волны через двойную щель, источник. Справа: результаты эксперимента по регистрации одиночных электронов после прохождения двойной щели. Источник: New Journal of Physics, Volume 15, March 2013.

Но если мы захотим узнать, через какую из щелей проходит электрон и поставим на против одной из них измерительный прибор, то интерференционная картина на экране пропадет, и мы увидим на экране только два пика. Все это вызывает недоумение, и может сложится впечатление, что существует какое-то особое правило, которое говорит электрону, что если никто не смотрит, то он распространяется в виде волны, а когда его пытаются измерить — превращается в локализованную частицу. Звучит очень странно, ведь держать столько сложных правил, для одного простого электрона — это совсем не в духе природы.

Карикатура, высмеивающая разделение явлений на квантовые и классические. Источник (http://www.bourbaphy.fr/zurek.pdf)

А что если мы применим только принцип суперпозиции, сможем ли мы получить те же наблюдаемые эффекты? Так если сначала мы имеем волновую функцию, которая описывает координату взаимодействия одиночного электрона с экраном $|\psi \rangle$ , то после прохождения через двойную щель, она будет представлять собой сумму двух волновых функций — прошедшей через щель $1$ и через щель $2$ , тогда общее состояние можно записать как суперпозицию этих двух состояний $|\psi \rangle =|\psi_1 \rangle +|\psi_2 \rangle$ .

В случае с одной волновой функцией, чтобы найти вероятность взаимодействия частицы в точке x_j мы находим произведение j-тых компонент бра и кет вектора, мнимые единицы при этом сокращаются, и мы получаем классическую вероятность:

$p(x_j)=|\psi(x_j)|^2= z _j^* z_j= |z_j|^2$

В случае с суперпозицией двух возможных маршрутов мы перемножаем уже сумму волновых функций:

$p(x_j)=|\psi_1(x_j)+\psi_2(x_j)|^2=$

В выражении выше кроме модулей комплексных чисел мы получили еще слагаемые вида: $ z1 _j^*z2 _j$ и $z2 _j^*z1 _j $ произведения разных комплексных чисел, результат которого будет зависеть от угла фазы $φ$ этих комлексных чисел:

$inline$z1z2=|z1|⋅|z2|[cos (φ1+φ2)+isin (φ1+φ2)]$inline$

Чтобы понять, как будут взаимодействовать фазы двух альтернативных маршрутов, представим фазу как стрелку, которая будет вращаться с заданной скоростью, мере распространения волны, один полный оборот стрелки будет соответствовать длине волны, а скорость вращения — частоте.

Черной стрелкой показано сравнение «скорости вращения» фаз двух волновых пакетов с разной частотой источник.

Поскольку две альтернативные волновые функции, получены в результате деления одной исходной, то разумно предположить, что их частота и длина волны будут одинаковыми и стрелки полученных волн будут вращаться с одинаковой скоростью. Исходя из этого, разность фаз, при встрече в точке на экране, будет зависеть только от разности расстояния пройденного волной до этой точки.

А значит, в точке, находящейся на равном удалении от каждого из отверстий, волны будут встречаться с одинаковым положением стрелок, то есть в одной фазе и в этом месте мы увидим пик в интерференционной картине, а в точке, где разность пройденных расстояний составит половину длинны волны — стрелки