Кто же такой этот многорукий бандит?21.09.2022 02:02

1. Поговорим о модели

Представьте на секунду, что вы очень азартный игрок, который только что попал в казино и не может выбрать, за какой игровой автомат ему сесть. Или один муравей из колонии, выбирающий по какому пути ему пойти на поиски пищи. Или даже вы — это целый маркетплейс, который думает, какую же цену, ему поставить на тот или иной товар!

На первый взгляд может показаться, что все эти странные ситуации никак не связаны. Но это только на первый взгляд. Если откинуть все необычность ситуации, то перед нами дилемма исследования-использования. Посудите сами: как азартный игрок, вы хотите найти автомат, дающий больше всего денег — это использование, но вы не знаете, какой это автомат и ищите его, дергая ручки и сравнивая выигрыши — это исследование. Как часто вам нужно подходить к игровому автомату, который, по вашему мнению, самый прибыльный, а как часто нужно сомневаться в этом и пробовать другие? Как часто муравью нужно идти по тому пути, где товарищи-муравьи уже протоптали тропинку, а как часто стоит рискнуть и пойти своей дорогой? Как часто нужно менять цену, чтобы поспевать за инфляцией и спросом пользователей, а еще при этом максимизировать прибыль?

Откинем красивые слова и перед тем, как кинуться в море алгоритмов и сбора данных, и формально опишем нашу модель:

E\left[R\left(a\right)\right]\rightarrow \max_a \\a\ \in \{ a_1,a_2,\ldots,\ a_n \}

Посмотрим на эту формулу внимательнее: во-первых, поскольку мы имеем дело со случайными явлениями (автоматы в казино, объемы продаж), то мы хотим максимизировать математическое ожидание. Это обозначает, что мы хотим найти такое действие a из множества действий {a1, a2, …, an}, которое будучи повторенным большое количество раз давало бы нам выигрыш больше, чем любое другое действие. То есть, если бы существовало много вселенных, в которых мы бы пробовали разные действия, то мы хотим жить в той, где в итоге выиграли больше всего! Но поскольку вселенная у нас только одна, то мы хотим понять, какое действие будет наилучшим за кратчайший срок. То есть, сравнивая различные подходы к этой задаче, мы можем сравнивать их на основе того, как быстро мы поймем какое действие верное, можем сравнивать, какая награда у нас оказалась «на руках» спустя некоторое количество попыток, или сколько мы потеряли из-за того, что выбирали не «оптимальное» действие. Это называется метрики, и о них мы поговорим чуть позже.

Теперь, когда мы избавились от излишних описаний ситуации и перешли к абстрактной (обобщенной) задаче, можно нырнуть в изучение различных подходов к решению этой задачи!

2. Как понять, какой подход лучше?

Как уже было сказано, нам нужны некоторые метрики, которые позволят нам сравнивать различные подходы к решению этой задачи. Больше того — внутри различных подходов к решению этой задачи существуют различные параметры, влияющие на эффективность данного подхода. По этой причине метрики очень важны!

Наиболее популярными являются 4 метрики, которые мы и будем использовать для сравнения подходов. Во-первых, это вероятность выбора оптимального действия:

{w_{opt}}_t=\begin{cases}1,{если\ мы\ выбрали\ оптимальное\ действие} \\ 0 \end{cases}

При первом взгляде на данную метрику кажется немного странным, что мы просто берем единицу или нолик в зависимости от того, какое действие мы выбрали. Но эта метрика начинает быть по-настоящему полезной, когда мы можем очень много раз повторить эксперимент, а затем усреднить полученные результаты (спойлер: так мы и будем делать). В таком случае мы получим реальную скорость нахождения оптимальной ручки, «отчищенную» от случайности, что, конечно же, очень полезно!

Но с другой стороны, мы все еще живем в единственной вселенной и зачастую у нас нет возможности много-много раз повторить эксперимент с нуля (да и не хочется, если от этого зависит наше благосостояние, как в случае с казино). В этом нам помогут еще три метрики. Они конечно тоже зависят от случайности и, если мы их усредним, будут более гладкими и отражающими ситуацию «в среднем», но и в случае с единственным экспериментом они помогут нам что-то понять о результатах этого эксперимента.

Следующие две метрики довольно тесно связаны между собой — это среднее вознаграждение за действие:

{r\_avg}_t=\ \frac{\sum_{i=1}^{t}R_i}{t}\

И суммарное вознаграждение:

{r\_total}_t=\ \sum_{i=1}^{t}R_i\

R­i — это награда, полученная за i-ое действие.

С данными метриками все понятно — первый показывает, сколько в среднем получаем за одно действие (и чем быстрее растет этот показатель — тем для нас лучше). А второй показывает сколько мы уже получили к некоторому моменту времени (и чем он больше в определенный момент времени — тем лучше).

И последняя, но не по значению, метрика — это метрика потерь (иногда английское слово regret переводится как сожаление):

reg_t=\ \sum_{i=1}^{t}{R_{opt}-R_t}\

Ropt — это средняя награда от выбора оптимального действия, то есть сколько бы мы получили, если бы изначально знали, какое действие будет наилучшим. Данная метрика показывает, сколько мы потеряли из-за того, что не знали, какое действие оптимальное. Понятно, как использовать эту метрику, если мы сами придумали эксперимент и знаем какая ручка оптимальная и сколько она дает в среднем. Но что же делать когда мы этого не знаем? Обычно, когда наступает время считать метрики, у нас уже есть некоторое представление, какое действие является оптимальным и какую награду мы в среднем получаем от этого действия. Отмечу так же, что эта метрика не так жестока, если у нас имеется действие очень близкое к оптимальному. В таком случае, если мы сойдемся к неоптимальному, но близкому к нему действию, то получим не сильно отличающееся значение потерь, чего нельзя сказать о вероятности выбора оптимального действия (первая метрика)

Теперь, когда у нас есть целых 4 инструмента для сравнения различных подходов к решению этой задачи, можно начать изучать и сами подходы!

3. Немного кода

Мне очень нравится фраза: «Пока ты не реализовал какой-то алгоритм в коде — ты не понял этот алгоритм». Так что здесь и далее будут приведены куски кода на языке Python, которые помогут лучше разобраться в данной теме!

Во-первых, зададим environment (окружающую среду), которая будет получать от нас действие, а в ответ на это действие будет с некоторой вероятностью выдавать определенную награду. Можно сделать более сложную и похожую на казино окружающую среду, например, чтобы награда выдавалась случайно из некоторого вероятностного распределения). Но такая награда выбрана, во-первых, из-за ее простоты, а во-вторых, потому что при большом количестве действий суммарная награда все равно будет распределена практически нормально. 

import numpy as np

class BanditEnv():
  def __init__(self, probs, reward):
    self.probs = probs
    self.reward = reward
    self._optimal_action = np.argmax(list(map(lambda x,y: x*y, probs, reward)))
    self._optimal_reward = np.max(list(map(lambda x,y: x*y, probs, reward)))

  def step(self, action):
    return self.reward[action] if np.random.rand(1).item() < self.probs[action] else 0

env = BanditEnv([0.3, 0.2, 0.1, 0.2, 0.9], [1, 1, 1, 1, 2])

В данном случае наша среда env создается с помощью класса BanditEnv в котором у нас 5 действий: с вероятностью 0.3 первое действие принесет награду 1, с вероятностью 0.2 второе действие принесет награду 1 и так далее. Очевидно, что наилучшим действием в данном случае является пятое, которое в среднем будет приносить награду 1.8.

Кроме этого, нам надо придумать стратегию, чтобы всегда выигрывать больше (это будет скелет нашего подхода к решению задачи). В этом нам поможет абстрактный класс. Он будет иметь общие для всех стратегий методы (__init__, update, reset), чтобы не переписывать их раз за разом. С помощью декоратора abstractmethod мы опишем метод, который должен быть реализован в каждой стратегии под тем же именем. Это поможет нам переиспользовать один и тот же код для разных методов. 

from abc import ABC, abstractmethod

class Strategy(ABC):
  def __init__(self, n_arms, epsilon):
    self.Q = np.zeros(n_arms)
    self.n = [0 for _ in range(n_arms)]
    self.epsilon = epsilon
    self.n_arms = n_arms
    
  @abstractmethod
  def make_action(self):
    pass
    
  def update(self, action, reward):
    self.n[action] += 1
    self.Q[action] = (self.Q[action] * (self.n[action]-1) + reward)/self.n[action]
        
  def reset(self):
    self.__init__(self.n_arms, self.epsilon)

Мы будем хранить среднюю награду за действие каждого действия в атрибуте Q, количество раз, когда мы предпринимали каждое действие в списке n, а epsilon — это некоторый параметр, который регулирует поведение алгоритма. Для каждого подхода этот параметр свой и мы будем обсуждать его смысл в каждом подходе. Метод update обновляет информацию, полученную в результате действия, а метод reset помогает сбрасывать все знания о среде, для чистоты следующего эксперимента.

Далее идут несколько непримечательных функций, которые прогоняют эпизоды, принимают решения на основе стратегий, собирают статистику и рисуют красивые графики, которые будут использоваться далее.

Технические функции

from tqdm import tqdm
import matplotlib.pyplot as plt

def run_n_episodes(env, strategy, n_episodes):
  w_opt_stat, r_avg_stat, r_total_stat, reg_stat = [],[],[],[]
  w_opt_times, total_reward, reg = 0, 0, 0
  for episode in range(1, n_episodes+1):
    action = strategy.make_action()
    reward = env.step(action)
    strategy.update(action, reward)
    w_opt_stat.append(1 if action==env._optimal_action else 0)
    total_reward += reward
    r_total_stat.append(total_reward)
    r_avg_stat.append(total_reward/episode)
    reg += env._optimal_reward - reward
    reg_stat.append(reg)
  return w_opt_stat, r_avg_stat, r_total_stat, reg_stat

def run_n_times(n_repeat, env, n_episodes, strategy):
  w_opt_stat_full, r_avg_stat_full = [],[]
  r_total_stat_full, reg_stat_full = [],[]
  for _ in tqdm(range(n_repeat)):
    strategy.reset()
    w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_episodes(env, 
                                                                    strategy,
                                                                    n_episodes)
    w_opt_stat_full.append(w_opt_stat)
    r_avg_stat_full.append(r_avg_stat)
    r_total_stat_full.append(r_total_stat)
    reg_stat_full.append(reg_stat)
  return np.array(w_opt_stat_full).mean(axis=0), np.array(r_avg_stat_full).mean(axis=0),\
       np.array(r_total_stat_full).mean(axis=0), np.array(reg_stat_full).mean(axis=0)

def plot_stats(w_opt_stat, r_avg_stat, r_total_stat, reg_stat, legends = False):
    plt.figure(figsize=(12, 7))
    plt.subplot(2, 2, 1)
    for i in w_opt_stat:
        plt.plot(i)
    plt.xlabel('t')
    plt.ylabel('w_opt')
    if legends: plt.legend(legends)
    plt.subplot(2, 2, 2)
    for i in r_avg_stat:
        plt.plot(i)
    plt.xlabel('t')
    plt.ylabel('r_avg')
    if legends: plt.legend(legends)
    plt.subplot(2, 2, 3)
    for i in r_total_stat:
        plt.plot(i)
    plt.xlabel('t')
    plt.ylabel('r_total')
    if legends: plt.legend(legends)
    plt.subplot(2, 2, 4)
    for i in reg_stat:
        plt.plot(i)
    plt.xlabel('t')
    plt.ylabel('reg')
    if legends: plt.legend(legends)

4. Сначала изучим, затем используем

Первой идеей, которая может возникнуть для решения этой задачи — давайте сначала просто случайно изучим все действия (пройдемся по всем игровым автоматам), а затем посмотрим, какой в среднем дает наибольшую награду и потом будем делать это действие не переставая!

И здесь возникает вопрос -, а сколько раз мы будем изучать эти действия до того, как начнем пользоваться? Ну для начала попробуем разное количество попыток. Например, 50 раз будем случайно выбирать действие. Давайте посмотрим, что же из этого получится!

Во-первых, напишем стратегию которая будет первые epsilon раз выбирать действие случайно, а затем выбирать то, которое в среднем нам давало лучшее решение. Для этого мы наследуемся от родительского класса Strategy, чтобы не писать уже готовые методы лишний раз и напишем, как должны приниматься решения в данной стратегии. В коде это выглядит следующим образом: 

class RandomСhoiceStrategy(Strategy):
    
    def make_action(self):
        if sum(self.n) < self.epsilon:
            return np.random.randint(self.n_arms)
        return np.argmax(self.Q)

А затем просто вызываем уже готовые функции для сбора статистики и отрисовки графиков

Код для отрисовки графиков

w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_times(100, env, 250, RandomСhoiceStrategy(5, 50))
plot_stats([w_opt_stat], [r_avg_stat], [r_total_stat], [reg_stat])

В результате получаются очень ожидаемые графики — до 50 действия вероятность выбора оптимального действия 20% или 1 раз из 5. Но потом мы вполне уверенно говорим, какое же действие оптимальное. Наша награда после 50-го действия начинает быстро расти, а потери до 50-го действия линейно растет, а затем становится постоянным, потому что мы перестаем выбирать неоптимальные действия:

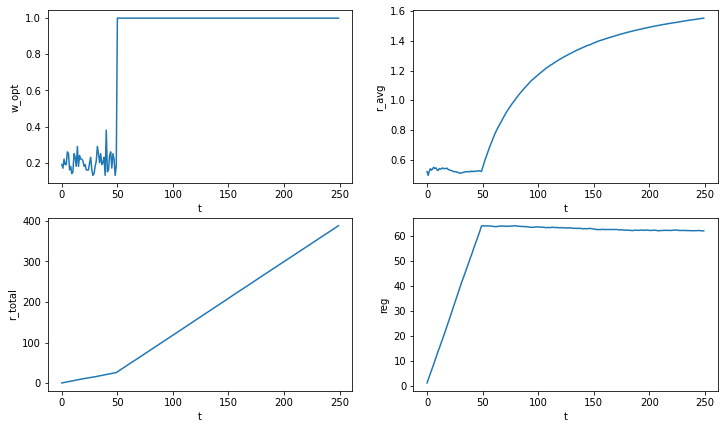Random Choice StrategyRandom Choice Strategy

Но может быть 50 это слишком много? Давайте попробуем разные количества и посмотрим, к чему это приведет.

Код для отрисовки графиков

w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full = [],[],[],[]
epsilons = [5, 10, 20, 30, 50]
for epsilon in epsilons:
  w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_times(500, env, 250, RandomСhoiceStrategy(5, epsilon))
  for f, l in zip([w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full],
                  [w_opt_stat, r_avg_stat, r_total_stat, reg_stat]):
    f.append(l)
plot_stats(w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full, epsilons)

Random Choice Strategy parametersRandom Choice Strategy parameters

Получается, что 5 и 10 — это слишком мало, поэтому не всегда наш алгоритм правильно успевает понять, какое же действие оптимальное. 20 раз тоже не дотягивает до чуть-чуть до 1, зато 30 и 50 оказались достаточными. С другой стороны, 20 первых попыток показывает наименьшую функцию потерь после 250 действий.  С увеличением количества возможных действий это число очевидно будет расти. В теории, зная количество действий и распределение наград за эти действия можно рассчитать оптимальное количество случайных действий. Это уже будет что-то похожее на A/B, A/B/C и тд. тестирование. Но наша проблема в том, что мы изначально не знаем, ничего о распределении наград за каждое действие. Можно усовершенствовать алгоритм — пусть он собирает некоторые знания о наградах, а когда наступит некоторого рода уверенность, полученная из данных, можно только использовать оптимальное действие. Примерно на такой идее строятся более продвинутые варианты решения данной проблемы, о которых мы и поговорим дальше!

5. Жадность не порок

Еще из простых идей сразу напрашивается следующая — давайте будем просто жадно использовать то действие, которое прямо сейчас кажется наилучшим. Ну, а чтобы не зацикливаться исключительно на одном действии — с некоторой вероятностью будем исследовать случайную ручку, вдруг она окажется лучше! Эта идея отражена в эпсилон-жадной стратегии. В виде кода это выглядит вот так: 

class EpsilonGreedyStrategy(Strategy):
    
    def make_action(self):
        if np.random.random() > self.epsilon:
            return np.argmax(self.Q)
        return np.random.randint(self.n_arms)

Попробуем с эпсилон равным 0.1. Это значит, что случайное действие будет выбираться в 10% случаев, а в противном случае будем выбирать действие, которое кажется наилучшим!

Код для отрисовки графиков

w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_times(1000, env, 250, EpsilonGreedyStrategy(5, 0.1))
plot_stats([w_opt_stat], [r_avg_stat], [r_total_stat], [reg_stat])

Epsilon Greedy StrategyEpsilon Greedy Strategy

На графике вероятности выбора оптимального действия видно, что с течением времени мы приближаемся к отметке 0.9. И это логично — когда наш алгоритм уже разобрался что к чему и какое действие оптимальное, он в 90% случаев будет выбирать его. Функция потерь в данном случае чуть хуже, чем у предыдущей стратегии. Но посмотрим, что будет, если попробовать другие параметры эпсилон

Код для отрисовки графиков

w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full = [],[],[],[]
epsilons = [0.1, 0.2, 0.3, 0.5]
for epsilon in epsilons:
  w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_times(500, env, 250, EpsilonGreedyStrategy(5, epsilon))
  for f, l in zip([w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full],
                  [w_opt_stat, r_avg_stat, r_total_stat, reg_stat]):
    f.append(l)
plot_stats(w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full, epsilons)

Epsilon Greedy Strategy parametersEpsilon Greedy Strategy parameters

Видно, что вероятность выбора оптимальной ручки сходится к 1 -эпсилон. То есть даже после большого количества времени мы не будем всегда выбирать только оптимальное действие. С одной стороны это плохо, потому что мы очевидно теряем награду, а с другой стороны вдруг в мире что-то поменялось и наше действие перестало быть наилучшим. В таком случае у нас есть возможность найти новое наилучшее действие. Как говорил Рене Декарт: «сомневаться нужно во всём, кроме собственного существования». Если же судить по метрике потерь — то наилучшим вариантом кажется эпсилон равный 0.2 — к моменту времени 250 она находится где-то на уровне 75, что уже сопоставимо с предыдущей стратегией!

6. Мягкий максимум

Очевидно, что у эпсилон-жадного алгоритма есть недостаток. Во-первых, не пользуемся всей, полученной информацией, а только думаем, какое же на данный момент нам действие кажется нам наилучшим. Во-вторых, не уменьшаем объем исследований после большого числа. Исправить эти недочеты пытается следующее семейство алгоритмов — softmax алгоритмы. Они основаны на функции softmax, знакомой многим исследователям данных. Она принимает на вход вектор и выглядит она вот так:

softmax\left(x\right)_i=\ \frac{e^{x_i}}{\sum_{k=1}^{K}e^{x_k}}\

Ее смысл в том, что она приводит любой вектор к вектору вероятностей и чем больше число в векторе, тем больше соответствующая ему вероятность. Соответственно, чем больше разрыв между числами, тем больше будет разрыв между вероятностями. Этим можно пользоваться, например, умножая или деля весь вектор на число, чтобы получить больший или меньший разрыв в вероятностях. А уже эти сами вероятности использовать для принятия решений о действии. Код новой стратегии выглядит так: 

def softmax(x):
  return np.exp(x)/np.sum(np.exp(x))

class SoftMaxStrategy(Strategy):
  def make_action(self):
    probs = softmax(self.Q/self.epsilon)
    return np.random.choice(self.n_arms, p=probs)

Мы определяем функцию softmax, а затем просто пользуемся ей для нахождений вероятностей действий в зависимости от того, сколько в среднем они нам приносили.

Код для отрисовки графиков

w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_times(200, env, 250, SoftMaxStrategy(5, 0.1))
plot_stats([w_opt_stat], [r_avg_stat], [r_total_stat], [reg_stat])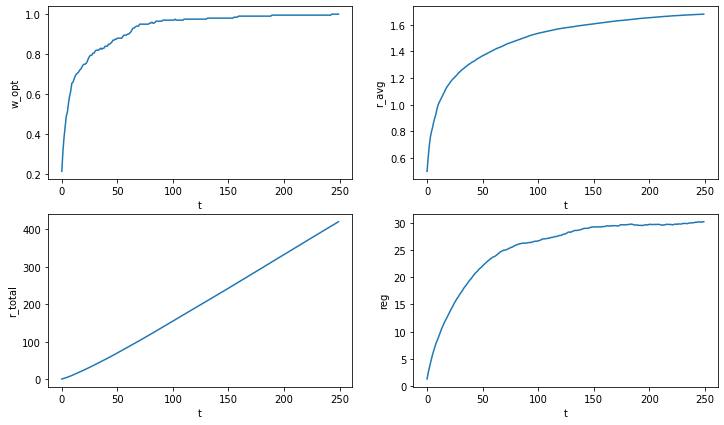

Soft Max StrategySoft Max Strategy

Видно, что такой подход дает результаты лучше чем предыдущие подходы! Вероятность выбора оптимальной ручки стремиться к единице, а наша функция потерь останавливается примерно в районе 30! Но можно изучить влияние различных параметров на результат:

Код для отрисовки графиков

w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full = [],[],[],[]
thetas = [0.1, 0.2, 0.3, 0.5]
for theta in thetas:
  w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_times(100, env, 250, SoftMaxStrategy(5, theta))
  for f, l in zip([w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full],
                  [w_opt_stat, r_avg_stat, r_total_stat, reg_stat]):
    f.append(l)
plot_stats(w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full, thetas)

Soft Max Strategy parametersSoft Max Strategy parameters

Для данного эксперимента наилучшими оказались параметры 0.2 и 0.3. Они показывают похожие результаты, как в вероятности выбора оптимальной ручки, так и для метрики потерь.

Кроме того, существует прием, который называется «симуляция отжига». Это пошло из физики, где функцию softmax (правда под другим именем) использовали для изучения горения и нагревания. Так вот, этот прием предлагает снижать коэффициент исследования в течение времени. Зачем нам исследовать, когда мы уже и так практически все знаем! В таком случае код будет выглядеть вот так: 

class AnnealingSoftMaxStrategy(Strategy):
    def make_action(self):
        theta = 1/np.log(np.sum(self.n)+2)
        probs = softmax(self.Q/theta)
        return np.random.choice(self.n_arms, p=probs)

Код для отрисовки графиков

w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_times(300, env, 250, AnnealingSoftMaxStrategy(5, 0))
plot_stats([w_opt_stat], [r_avg_stat], [r_total_stat], [reg_stat])

Annealing Soft Max StrategyAnnealing Soft Max Strategy

Результат на лицо — мы довольно быстро перестаем исследовать, так как понимаем, что к чему и получаем очень хорошие метрики! И приятный бонус — нам не нужно задумываться о том, какой параметр брать!

7. Доверительные интервалы

Следующий подход к решению нашей задачи является одним из наиболее популярных, потому что у него есть некоторое доказательство его оптимальности. А если быть точнее, то доказано, что метрика потерь растет со скоростью О (log (t)). Здесь я не буду приводить доказательство и выводы, поэтому особо любопытных отсылаю к более академическим и лучше англоязычным источникам.

Данный метод называется — алгоритм верхней доверительной границы или UCB по английский. Его суть заключается в том, что мы выбираем действие с наибольшей верхней доверительной границей, которая рассчитывается по формуле:

UCB_i=q_i\ + \sqrt{c *\ \frac{\log{t}}{n_i} }

В данной формуле:

q — это среднее вознаграждение от использования i-ого действия

c — параметр, отвечающий за ширину доверительного интервала, а значит за то, как часто мы исследуем новые значения

t — момент времени наблюдения

ni — количество раз, когда мы использовали i-ое действие.

Логика такая — чем больше мы используем какое-то действие (знаменатель), тем меньше становится доверительный интервал. Мы становимся уверены, что знаем реальную среднюю награду за данное действие — верхняя доверительная граница снижается. В это же время для действий, которые мы не используем, доверительный интервал растет за счет роста знаменателя, но растет медленно, потому что логарифм. И в один момент может оказаться, что, то действие, которое нам казалось оптимальным, уже нам таким и не кажется, нас привлекают менее исследованные действия. И все по новой. Затем мы можем вернуться обратно к изначальному действию. Колесо Сансары дало оборот.  И вот таким образом мы и решаем дилемму исследования-использования. Код для этой стратегии выглядит так: 

class UBCStrategy(Strategy):
    
    def make_action(self):
        c = np.sqrt(self.epsilon * np.log(np.sum(self.n)+1)/(np.array(self.n)+1))
        upper_bounds = self.Q + c
        return np.argmax(upper_bounds)

Код для отрисовки графиков

w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_times(400, env, 250, UBC1Strategy(5, 2))
plot_stats([w_opt_stat], [r_avg_stat], [r_total_stat], [reg_stat])

UBC StrategyUBC Strategy

На графиках отчетливо видно, в какой момент в среднем наш алгоритм бросает использовать оптимальное действие, которое нашел до этого и довольно быстро, и начинает использовать другие. Это происходит где-то между 50 и 100 моментом времени. Но даже в таком случае он показывает хорошие результаты! А вот как он работает с другими параметрами.

Код для отрисовки графиков

w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full = [],[],[],[]
params = [1, 2, 3, 5]
for param in params:
    w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_times(100, env, 250, UBC1Strategy(5, param))
    for f, l in zip([w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full],
                  [w_opt_stat, r_avg_stat, r_total_stat, reg_stat]):
        f.append(l)
plot_stats(w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full, params)

UBC Strategy parametrsUBC Strategy parametrs

Для данной ситуации лучшим и наиболее стабильным является параметр c равный 1. Иногда параметр выносится в название алгоритма, и тогда пишут UCB1, UCB2 и так далее. И данный подход к решению задачи о многоруком бандите является одним из двух наиболее частых и популярных!

8. Байесовские бандиты

Вторым частым и популярным подходом к решению задачи о многоруком бандите является алгоритм Выборка Томпсона и основан данный алгоритм на байесовской статистике! Он более сложный для глубокого понимания, чем предыдущие, но зато в некоторых случаях дает просто потрясающие результаты. По этой причине нужно сделать лирическое отступление и очень коротко поговорить о байесовской статистике. Если это кажется излишним и хочется увидеть сам алгоритм и результаты, то можно просто пропустить следующую пару абзацев.  Само собой здесь будет очень сжатый разговор про очень объемную тему, поэтому заинтересовавшихся отсылаю к замечательным книгам:

  • Курт Уилл. Байесовская статистика: Star Wars, LEGO, резиновые уточки и многое другое — для начинающих;

  • Освальдо Мартин. Байесовский анализ на Python — для продвинутых

В них дается хорошее понимание что такое байесовская статистика и чем она отличается от классической.

Но вернемся к нашей теме. Во-первых, постараемся понять, на каких идеях строится байесовская статистика. В первую очередь это теорема Байеса:

P\left(H\middle| D\right)=\ \frac{P\left(D\middle| H\right)\ast P\left(H\right)}{P\left(D\right)}

Буквой H обозначается гипотеза, буквой D — данные, полученные в результате наблюдения. Слева от знака равенства — вероятность того, что наша гипотеза верна, при условии полученных данных, или лучше сказать наша уверенность в гипотезе H (потому что байесовская статистика рассматривает вероятность как степень уверенности в чем-либо). Справа в знаменателе — вероятность получить такой результат, при условии, что наша гипотеза верная и наша уверенность в гипотезе до получения результатов. Знаменатель, грубо говоря, в такой интерпретации выступает просто поправочным коэффициентом (если говорить строго, то знаменатель это вероятность получить те результаты, которые мы получили, при всех возможных гипотезах). Вероятность P (H) называется априорной вероятностью — то, что мы думали до опыта, вероятность P (H|D) называется апостериорной вероятностью — то, что мы думаем после опыта, вероятность P (D|H) называется правдоподобием. По факту байесовская статистика предлагает нам формальный метод пересмотра своего мнения на основе полученных данных.

Разберем на примере. Вам на день рождения подарили монетку для принятия решений, но вы слишком хорошо знаете человека, который вам ее подарил — он постоянно пытается разыграть вас! Возможно в этот раз он подарил нечестную монетку, которая всегда будет выпадать орлом и вы решаете ее проверить! До того, как вы начали эксперимент вы совершенно не знаете, что ждать — монетка либо честная и дает орлов в 50% случаев, либо нечестная и орлы выпадают, например, в 90% случаев. Поэтому вероятность, что монетка честная для вас равна 50%. И вот после 5 бросков у вас есть 5 орлов подряд. Казалось бы все понятно — вас хотят разыграть! Но не будем спешить с выводами и воспользуемся теоремой Байеса. Априорная вероятность равна 0.5,  вероятность выпадения 5 орлов при честной монетке равна (0.5)5 тогда числитель равен (0.5)6. Знаменатель равен ((0.5)5 + (0.9)5)*0.5 (Здесь я отсылаю вас к учебникам по теории вероятностей или книгам, которые советовал ранее). В таком случае, вероятность, что монетка честная равна примерно 0,05 или 5%.  Это наша апостериорная вероятность, того, что монетка честная. Конечно, мы почти уверены, что нас пытаются разыграть, но все равно на 5% мы верим нашему другу.

Это был простейший пример применения байесовской статистики. Априорные и апостериорные вероятности могут быть непрерывными, что не сильно меняет общую логику, но сильно усложняет вычисления. В общем случае от этого никуда не деться, но существуют частные случаи, которые помогают сильно упростить вычисления и код, они называются сопряженные вероятности. (отсылаю любопытных к статье в википедии (отсылаю любопытных к статье в Википедии:  Сопряжённое априорное распределение). Если коротко, то при использовании сопряженных вероятностей априорное и апостериорное распределения имеют одну и ту же функцию распределения, но с разными параметрами.

Вернемся к основному объекту нашего разговора — задаче о многоруких бандитах, и на ее примере разберём, как используются сопряженные вероятности. Рассмотрим два вида алгоритма — в первом будем считать, что награда имеет распределение Бернулли (то есть либо 1 с вероятностью p, либо 0 с вероятностью 1-p), а во втором, что награда имеет нормальное распределение.

Итак, в первом случае мы имеем дело с наградой, которая распределена согласно закону Бернулли, а значит сопряженное с ним распределение — бета-распределение (это можно понять из таблички на страничке в википедии, на которую я дал ссылку выше!). Опять же, не буду подробно останавливаться на разговоре о бета-распределении (любопытным — книги), но скажу лишь, что это распределение находится от 0 до 1 (а значит задает вероятность), и зависит от 2 параметров: альфа и бета, которые интерпретируются как количество удачных (в нашем случае мы получили награду 1) и неудачных (получили награду 0) соответственно. Каждому действию присваивается свое распределение (изначально у всех одинаковые параметры), из этих распределений случайно делаем выборку в 1 элемент и сравниваем их между собой. В итоге — выбираем то действие, у которого наибольшее значение случайно выбранного числа, а потом, в зависимости от полученной награды, обновляем параметры распределения. Код выглядит вот так: 

import scipy.stats as stats

class BayesianStrategy_Bin(Strategy):
  def __init__(self, n_arms):
    self.n_arms = n_arms
    self.a = np.ones(n_arms)
    self.b = np.ones(n_arms)
    self.disr = stats.distributions.beta
        
  def make_action(self):
    samples = self.disr.rvs(self.a, self.b)
    return np.argmax(samples)
    
  def update(self, action, reward):
    if reward:
      self.a[action] += 1
    else:
      self.b[action] += 1
        
  def reset(self):
    self.__init__(self.n_arms)

А смысл у этих манипуляций такой: чем больше у бета-распределения параметр альфа (количество успешных действий), тем ближе распределение к 0, и наоборот — чем больше бета (количество неуспешных действий), тем ближе к 1. Кроме того, чем больше сумма альфа и бета, тем меньше дисперсия. Это выливается в то, что выборка из распределения, связанного с лучшим действием довольно быстро начнет выдавать выборку с большими значениями, а значит и выбирать это действие будут чаще!

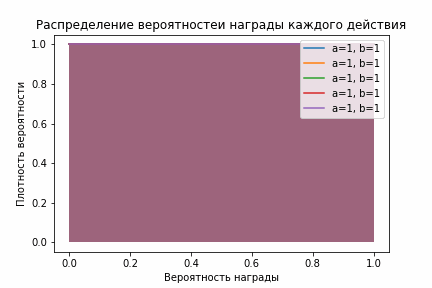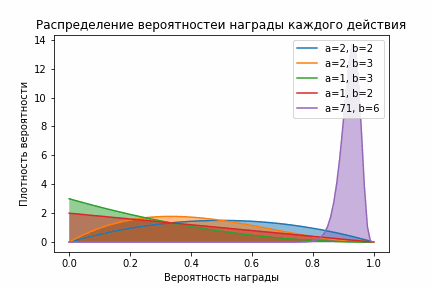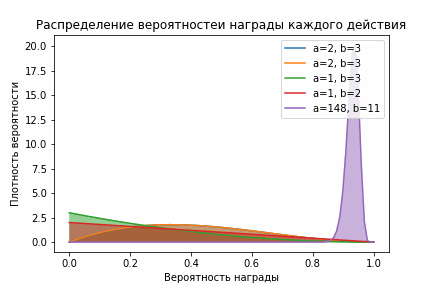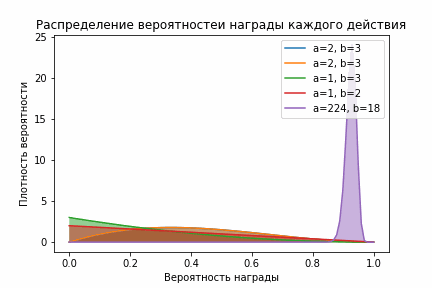Beta-распределениеBeta-распределение

На гифке видно, что, после того как алгоритм немного исследовал все действия, фиолетовое распределении становится сконцентрированным справа, а значит выборки из него стабильно будут больше выборок из остальных распределений.

Для данного алгоритма нам нужно создать другую окружающую среду: 

env = BanditEnv([0.3, 0.2, 0.1, 0.2, 0.9], [1,1,1,1,1])

А метрики работы данного алгоритма выглядят так:

Код для отрисовки графиков

w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_times(150, env, 250, BayesianStrategy_Bin(5))
plot_stats([w_opt_stat], [r_avg_stat], [r_total_stat], [reg_stat])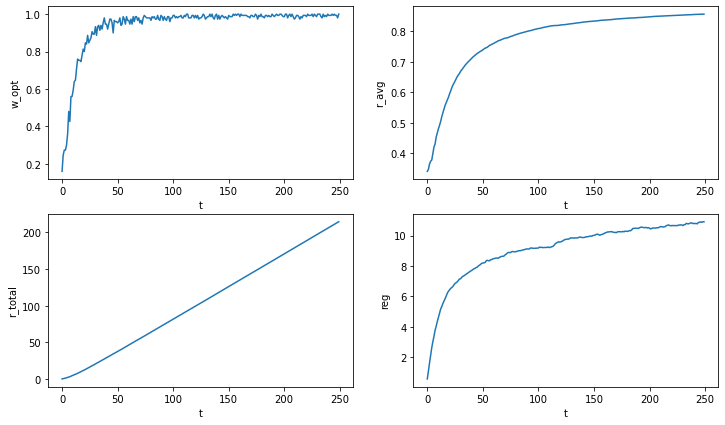

Bayesian Strategy (Binary)Bayesian Strategy (Binary)

Как по мне, очень крутые результаты!

С нормальным распределением очень похожая история: мы предполагаем, что выигрыш распределен нормально, сопряженное распределение для нормального распределение — нормальное (концентрация нормального в одном предложении зашкаливает). Параметры в нормальном распределении отвечают за центр распределение (μ — среднее) и за его ширину (σ — стандартное отклонение). Эти параметры и обновляются от результата эксперимента.

Нормальное распределениеНормальное распределение

Здесь тоже отчетливо видно, как фиолетовое распределение очень быстро стало правее остальных. Кроме этого оно стало быстро стало довольно узким и выборки из него были больше всех остальных. С одной стороны, это здорово, потому что мы быстро перестали исследовать и начали использовать. Но с другой стороны, может быть мы недостаточно исследовали и на самом деле следует поискать еще? Чтобы увеличить время исследования и заставить алгоритм исследовать все действия используют следующий прием — ставят немного завышенное начальное значение. В таком случае в результате исследования мы будем больше узнавать о распределении награды и двигаться влево, давая тем самым алгоритму возможность исследовать другие действия. Визуально это выглядит вот так:

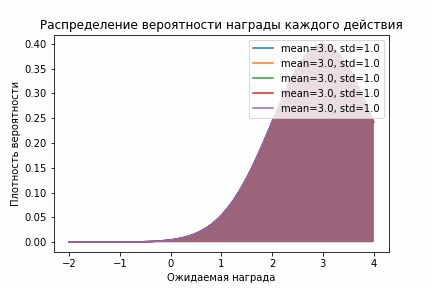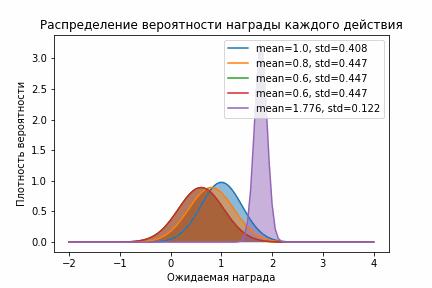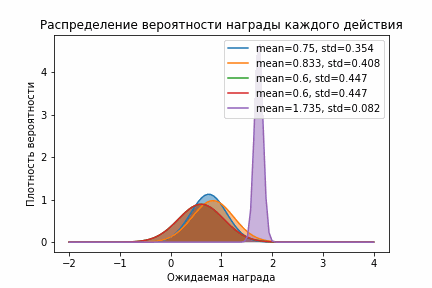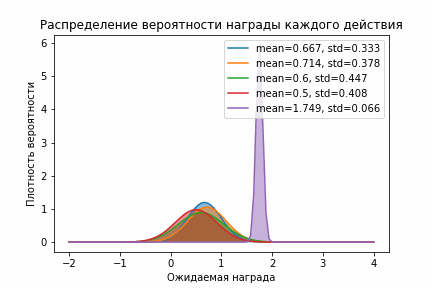Нормальное распределение со смещениемНормальное распределение со смещением

Вот так уверенность в том, что мы ничего не упустили намного больше!

 О том как они обновляются призываю вас почитать на той же страницы в википедии, потому что формулы там дольно объемные. В результате код выглядит вот так: 

class BayesianStrategy_Norm(Strategy):
  def __init__(self, n_arms, sigma):
    self.n_arms = n_arms
    self.means = np.ones(n_arms) * 3
    self.tay = 1/(np.ones(n_arms) * sigma)**2
    self.tay_likelihood = 1/(sigma**2)
    self.disr = stats.distributions.norm
    self.sigma = sigma
        
  def make_action(self):
    samples = self.disr.rvs(self.means, np.sqrt(1/self.tay))
    return np.argmax(samples)
   
  def update(self, action, reward):
    self.means[action] = (self.tay[action]*self.means[action] + self.tay_likelihood*reward)/(self.tay[action] + self.tay_likelihood)
    self.tay[action] = self.tay[action] + self.tay_likelihood
        
  def reset(self):
    self.__init__(self.n_arms, self.sigma)

Здесь используется определение нормального распределения через тау, а не через сигму просто потому, что это упрощает расчёты.

Код для отрисовки графиков

env = BanditEnv([0.3, 0.2, 0.1, 0.2, 0.9], [1,1,1,1,2])
w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_times(150, env, 250, BayesianStrategy_Norm(5, 2))
plot_stats([w_opt_stat], [r_avg_stat], [r_total_stat], [reg_stat])

Bayesian Strategy (Norm)Bayesian Strategy (Norm)

Результаты не такие хорошие, как для распределения Бернулли, но это можно объяснить тем, что здесь и окружающая среда другая, и предположение о нормальности несколько натянуто за уши или параметры подобраны не очень хорошо, поэтому посмотрим на поведение алгоритма при других параметрах.

Код для отрисовки графиков

w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full = [],[],[],[]
params = [0.5, 1, 2, 5]
for param in params:
    w_opt_stat, r_avg_stat, r_total_stat, reg_stat = run_n_times(100, env, 250, BayesianStrategy_Norm(5, param))
    for f, l in zip([w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full],
                  [w_opt_stat, r_avg_stat, r_total_stat, reg_stat]):
        f.append(l)
plot_stats(w_opt_stat_full, r_avg_stat_full, r_total_stat_full, reg_stat_full, params)

Bayesian Strategy (Norm) parametersBayesian Strategy (Norm) parameters

Вот теперь результаты на порядок лучше! Но все познается в сравнении, поэтому посмотрим на метрики различных решений на одном графике!

9. Все познается в сравнении

Теперь, когда мы рассмотрели все наиболее популярные алгоритмы решения задачи о многоруком бандите, настало время сравнить их. Так как в предыдущей части мы исследовали 2 различных окружающих среды. В одной среде награды распределены по закону Бернулли, а во второй предполагали, что награды распределены нормально, значит и сравнивать алгоритмы будем в 2 различных средах. Для начала посмотрим второй вариант:

Код для отрисовки графиков

env = BanditEnv([0.3, 0.2, 0.1, 0.2, 0.9], [1, 1, 1, 1, 2])
w_opt_stat_full, r_
    
            
© Habrahabr.ru