Краткий курс компьютерной графики: задание карт нормалей в касательном пространстве
Дошли руки написать очередное дополнение к моему краткому курсу компьютерной графики. Итак, тема для очередного разговора — использование карт нормалей. В чём основное отличие использования карт нормалей от затенения Фонга? Основная разница в плотности задания информации. Для затенения Фонга мы использовали нормальные вектора, заданные к каждой вершине нашей полигональной сетки, интерполируя нормали внутри треугольников. Использование же карт нормалей позволяет задавать нормали для каждой точки нашей поверхности, а не лишь изредка, что просто драматическим образом влияет на детализацию изображений.
В принципе, в лекции про шейдеры мы уже использовали карту нормалей, но только заданную в глобальной системе координат. Сейчас же разговор пойдёт про касательное пространство. Итак, вот две текстуры, левая задана в глобальном пространстве (RGB напрямую превращается в вектор XYZ), а правая — в касательном.
Чтобы использовать нормаль, заданную в касательном пространстве, для рисуемого пикселя мы вычисляем касательный репер (репер Френе). В этом репере один вектор (z) ортогонален поверхности, а два других задают касательную плоскость к поверхности. Затем читаем нормальный вектор из текстуры, и преобразуем его координаты из только что вычисленного репера в глобальный. Поскольку карта нормалей чаще всего задаёт лишь небольшое возмущение нормали, то доминирующий цвет у текстуры синий.
Казалось бы, зачем такие сложности? Почему не пользоваться простым глобальным репером как раньше? Представьте себе, что мы хотим анимировать нашу модель. Например, я взял нашего старого знакомого негра и открыл ему рот. Очевидно, что у модифицированной поверхности должны быть и другие нормали!
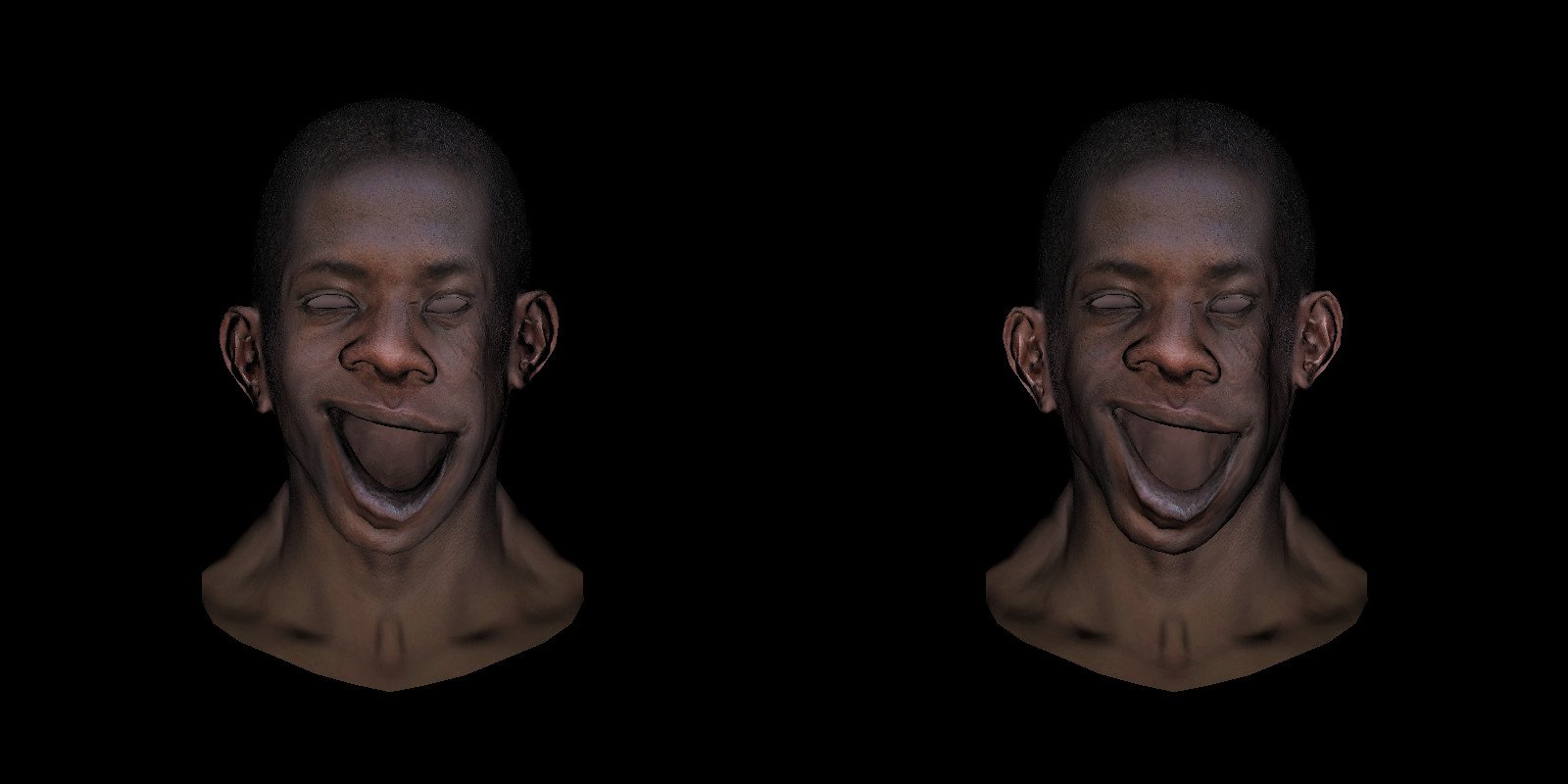
Вот слева модель, в которой рот открыт, а карта нормалей (глобальная) изменена не была. Посмотрите на слизистую нижней губы. Свет бьёт прямо в лицо, у модели с закрытым ртом слизистая, разумеется, не была освещена никак. Рот открылся, а она по-прежнему не освещена… Правая картинка посчитана с использованием карты нормалей, заданной в касательном пространстве.
Итак, если у нас есть анимированная модель, то для задания карты нормалей в глобальном пространстве нам нужна одна текстура на каждый кадр анимации. А поскольку касательное пространство натурально следует за поверхностью, то такой текстуры нам достаточно одной!
Вот второй пример:

Это текстуры для модели Диабло. Обратите внимание, что на текстуре видна только одна рука. И только одна половина хвоста. Художник использовал одну и ту же текстуру для левой и правой руки, и одну и ту же текстуру для левой и правой части хвоста. (К слову сказать, это то, что помешало нам посчитать ambient occlusion.) А это означает, что в глобальной системе координат я могу задать нормальные вектора либо для левой руки, либо для правой. Но никак не для двух разом!
Итак, заканчиваем с мотивацией и переходим непосредственно к вычислениям.
Итак, давайте посмотрим на отправную точку. Шейдер очень простой, это затенение Фонга.
struct Shader : public IShader {
mat<2,3,float> varying_uv; // triangle uv coordinates, written by the vertex shader, read by the fragment shader
mat<3,3,float> varying_nrm; // normal per vertex to be interpolated by FS
virtual Vec4f vertex(int iface, int nthvert) {
varying_uv.set_col(nthvert, model->uv(iface, nthvert));
varying_nrm.set_col(nthvert, proj<3>((Projection*ModelView).invert_transpose()*embed<4>(model->normal(iface, nthvert), 0.f)));
Vec4f gl_Vertex = Projection*ModelView*embed<4>(model->vert(iface, nthvert));
varying_tri.set_col(nthvert, gl_Vertex);
return gl_Vertex;
}
virtual bool fragment(Vec3f bar, TGAColor &color) {
Vec3f bn = (varying_nrm*bar).normalize();
Vec2f uv = varying_uv*bar;
float diff = std::max(0.f, bn*light_dir);
color = model->diffuse(uv)*diff;
return false;
}
};
Вот результат работы шейдера:

Для простоты обучения и отладки я уберу текстуру кожи и применю простейшую регулярную сетку с горизонтальными красными и вертикальными синими линиями:

Давайте посмотрим, как работает наш шейдер Фонга на примере этой картинки:
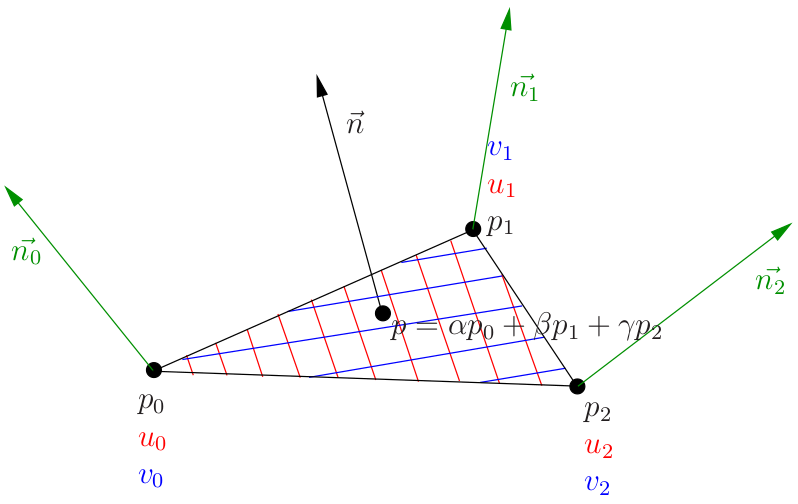
Итак, для каждой вершины треугольника у нас даны её координаты p, её текстурные координаты uv и нормальные вектора к вершинам n. Для отрисовки каждого пикселя растеризатор нам даёт барицентрические координаты пикселя (альфа, бета, гамма). Это означает, что текущий пиксель имеет пространственные координаты p = альфа p0 + бета p1 + гамма p2. Мы интерполируем текстурные координаты ровно так же, затем интерполируем и вектор нормали:
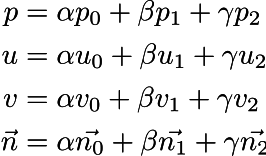
Обратите внимание, что красные и синии линии — это изолинии u и v, соответственно. Итак, для каждой точки нашей поверхности у нас задаётся (скользящий) репер Френе, у которого ось x параллельна красным линиям, ось y параллельна синим, а z ортогональная поверхности. Именно в этом репере и задаются нормальные вектора.
Итак, наша задача — для каждого рисуемого пикселя посчитать тройку векторов, задающую репер Френе. Давайте для начала отвлечёмся и представим, что в нашем пространстве задана линейная функция f, которая каждой точке (x, y, z) сопоставляет вещественное число f (x, y, z) = Ax + By + Cz + D. Единственное, что мы не знаем чисел (A, B, C, D), но знаем значение функции в вершинах некоторого треугольника (p0, p1, p2):
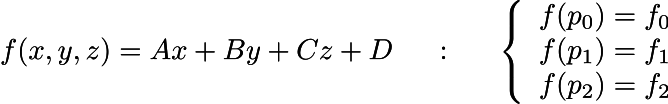
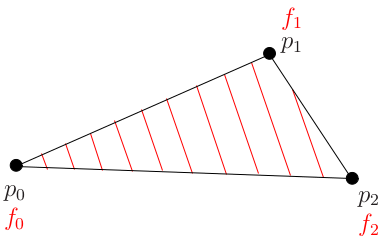
Можно представлять себе, что f — это просто высота некоторой наклонной плоскости. Мы фиксируем три разные точки на плоскости и знаем значения высот в этих точках. Красные линии на треугольнике показывают изолинии высоты: изолиния для высоты f0, для высоты f0+1 метр, f0+2 метра и т.д. Для линейной функции все эти изолинии, очевидно, являются параллельными прямыми.
Что нам интересно это даже не столько направление изолиний, сколько направление, им ортогональное. Если мы передвигаемся вдоль какой-то изолинии, то высота не меняется (спасибо, капитан), если мы отклоняем направление чуть-чуть от изолинии, то высота начинает меняться, а самое большое изменение на единицу высоты будет тогда, когда мы будем передвигаться в направлении, ортогональном изолиниям.
Вспоминаем, что направление наискорейшего подъёма для какой-то функции есть не что иное, как её градиент. Для линейной функции f (x, y, z) = Ax + By + Cz + D её градиент — это постоянный вектор (A, B, C). Логично, что он постоянный, так как любая точка плоскости наклонена одинаково. Напоминаю, что мы не знаем чисел (A, B, C). Мы знаем только значение нашей функции в трёх разных точках. Можем ли мы восстановить A, B и С? Конечно.
Итак, у нас есть три точки p0, p1, p2 и три значения функции f0, f1, f2. Нам интересно найти вектор (A, B, C), дающий направление наискорейшего роста функции f. Давайте для удобства будем рассматривать функцию g (p), которая задаётся как g (p) = f (p) — f (p0):
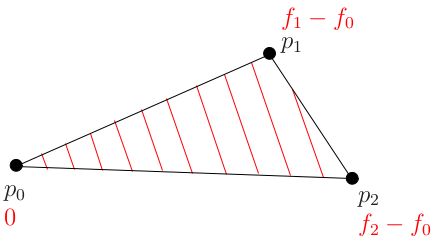
Очевидно, что мы просто переместили нашу наклонную плоскость, не изменив её наклона, поэтому направление наискорейшего роста для функции g будет совпадат с направлением наискорейшего роста функции f.
Давайте перепишем определение функции g:
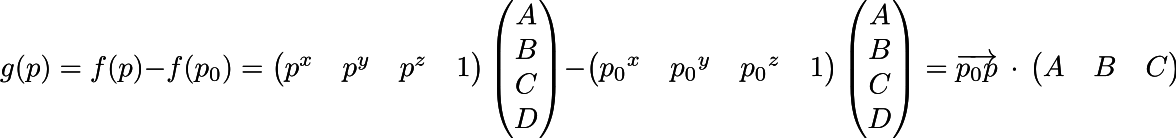
Обратите внимание, что верхний индекс p^x — это координата x точки p, а не степень. То есть, функция g — это всего-навсего скалярное произведение вектора, соединяющего текущую точку p с точкой p0 и вектора (A, B, C). Но ведь мы по-прежнему не знаем (A, B, C)! Не страшно, сейчас их найдём.
Итак, что нам известно? Нам известно, что если от точки p0 мы пойдём в p2, то функция g будет равняться f2-f0. Иными словами, скалярное произведение между векторами p2-p0 и ABC равняется f2-f0. То же самое для dot (p1-p0, ABC)=f1-f0. То есть, мы ищем вектор (ABC), который одновременно ортогонален нормали к треугольнику и имеет эти два ограничения на скалярные произведения:
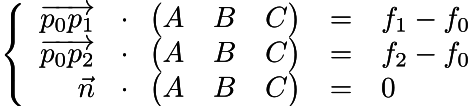
Запишем то же самое в матричной форме:
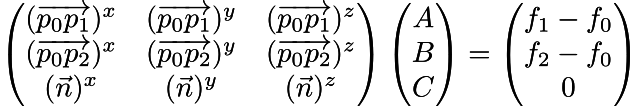
То есть, мы получили матричное уравнение Ax = b, которое легко решается:
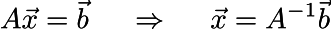
Обратите внимание, что я использовал литеру А в двух смыслах, значение должно быть ясно из контекста. То есть, наша 3×3 матрица A, помноженная на неизвестный вектор x=(A, B, C), даёт вектор b = (f1-f0, f2-f0, 0). Неизвестный вектор находится умножением матрицы, обратной к A, на вектор b.
Обратите внимание, что в матрице A нет ничего, что зависит от функции f! Там содержится только информация о геометрии треугольника.
Итого, репер Френе — это тройка векторов (i, j, n), где n — это вектор нормали, а i и j могут быть подсчитаны следующим образом:
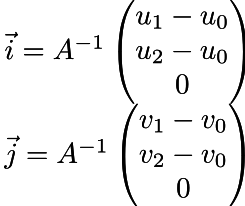
Вот финальный код, использующий карты нормалей, заданные в касательном пространстве, а тут можно найти изменения в коде по сравнению с тонировкой Фонга.
Там всё довольно прямолинейно, я вычисляю матрицу A:
mat<3,3,float> A;
A[0] = ndc_tri.col(1) - ndc_tri.col(0);
A[1] = ndc_tri.col(2) - ndc_tri.col(0);
A[2] = bn;
Затем вычисляю вектора репера Френе:
mat<3,3,float> AI = A.invert();
Vec3f i = AI * Vec3f(varying_uv[0][1] - varying_uv[0][0], varying_uv[0][2] - varying_uv[0][0], 0);
Vec3f j = AI * Vec3f(varying_uv[1][1] - varying_uv[1][0], varying_uv[1][2] - varying_uv[1][0], 0);
Ну, а однажды их вычислив, читаю нормаль из текстуры, и делаю простейшее преобразование координат из репера Френе в глобальный репер.
Если что, то преобразования координат я уже описывал.
Вот финальный рендер, сравните детализацию с тонировкой Фонга:
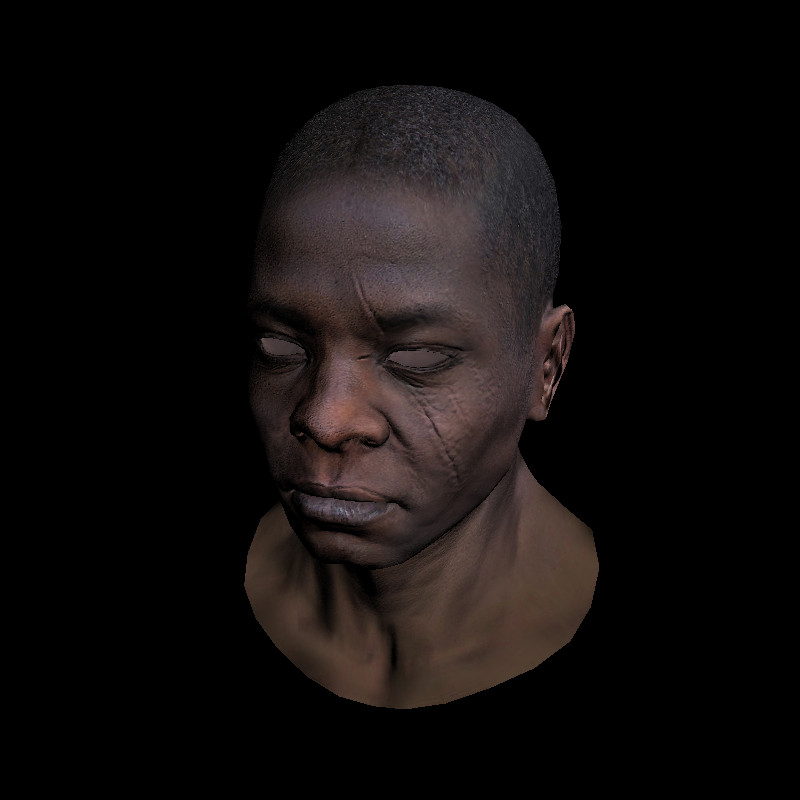
Самое время вспомнить, как отрисовываются линии. Наложите на модель регулярную красно-синюю сетку и для всех вершин отрисуйте полученные вектора (i, j), они должны хорошо совпасть с направлением красно-синих линий текстуры.
Happy coding!
