Космология — Стэнфорд. Конспект. Лекция 1

Эта статья открывает серию статей с конспектами лекций по Космологии Стэнфордского университета. Сами лекции на английском языке доступны по ссылке: Cosmology (2013) — Leonard Susskind — Stanford University. Лектор Leonard Susskind объясняет очень доступно и увлекательно. Талантливый человек и отличный преподаватель.
Стэнфордский университет знаменит еще и тем, что там работает наш выдающийся соотечественник Андрей Линде, который, вероятно, вскоре будет удостоен Нобелевской премии по физике за вклад в современную космологию. Кому интересно, советую посмотреть его публичную лекцию Многоликая Вселенная.
Этот конспект — моя попытка самообразования. Я бы его все равно написал для себя в тетрадке. Но вот решил совмещать приятное с полезным. Надеюсь, что кому-то это будет тоже интересно.
Сразу оговорюсь, что я старался конспектировать близко к оригинальному тексту. Однако, кое-где я позволил себе дополнить или обобщить высказывания лектора, опираясь на свой собственный опыт специалиста физика. Это делалось исключительно для того чтобы способствовать пониманию, осмыслению и усвоению материала.
В этой статье вашему вниманию предлагается конспект лекции 1. Постепенно будут появляться продолжения.
Исторический обзор
Космология — это очень древний предмет. История космологии насчитывает тысячи лет. В особенности, древние греки знали о космологии очень давно.
В этих лекциях освещается период времени не далее чем вторая половина ХХ века, когда Эдвин Хаббл открыл закон расширения Вселенной.
Если говорить о космологии как о науке — то это достаточно новая область знаний. Современная космология берет начало с момента обнаружения микроволнового реликтового излучения и формулировки теории большого взрыва. А это случилось только в 1960-х.
До этого момента космология не была разделом физики, а в большей степени принадлежала к естественным наукам. То есть, в космологии господствовал феноменологический подход: наблюдение, измерение, классификация, составление каталогов и т.д.
В то время точность измерений была невысока. И поэтому невозможно было формулировать точные утверждения. Существовали уравнения, но они были неверными и неточными. Физики были всегда вовлечены в процесс изучения, поскольку звезды, галактики и другие небесные тела обладают физическими характеристиками такими как угловой момент, например. Также были вовлечены и физические химики, поскольку небесные тела имеют химический состав.
Однако, отношение ко Вселенной самой по себе как к физическому объекту, Вселенная как система, которую следует изучать математически с помощью набора физических принципов и соответствующих точных правильных уравнений — это подход сравнительно молодой.
Свойства Вселенной
В этих лекциях Вселенная рассматривается как физическая система. И мы будем изучать ее при помощи уравнений. Мы можем начать изучение Вселенной с некоторых общих наблюдений.
Изотропия
Итак, первое наблюдение, которое, вообще говоря, может и не быть абсолютно точным, так же как и вся физика не является абсолютно точной — это то, что Вселенная изотропна.
Изотропия означает, что Вселенная выглядит одинаково в любом направлении. Конечно, это справедливо лишь для достаточно больших расстояний. Если смотреть слишком близко, то изотропия может не наблюдаться из-за локальных неоднородностей, например из-за формы нашей галактики.
Однородность
Если Вселенная изотропна, то можно утверждать с большой долей уверенности, что Вселенная также должна быть и однородна. Однородность означает одинаковость не в каждом направлении, а в каждом месте. То есть на большом масштабе Вселенная выглядит одинаково независимо от того, где находится наблюдатель — в нашей галактике или же в какой-то другой, которая далеко-далеко от нас.
Галактики
Галактики на масштабе Вселенной эффективно являются точками сосредоточения массы. Мы можем относиться к ним как материальным точкам. Приблизительное число галактик в видимой части Вселенной — сто миллиардов . В свою очередь, каждая галактика содержит также примерно
сто миллиардов звезд. Надо помнить, что это число галактик только внутри той сферы, которую мы можем видеть. Только так далеко, как могут увидеть астрономы при помощи телескопов. То есть, самое далекое, что мы можем видеть находится на расстоянии, откуда свет успел долететь до нас за все время существования Вселенной: порядка 13 миллиардов лет.
Интересный факт. Полное число звезд в видимой части Вселенной
, и если у каждой звезды в среднем имеется по 10 планет, то получается
— число Авогадро планет во Вселенной. Планетарный моль вещества! (лектор смеется)
Аргумент против однородности Вселенной. Опровержение
Рассмотрим кусочек Вселенной, где находимся мы. Мы точно знаем, потому что видим, что Вселенная изотропна. Мы предполагаем, что Вселенная также однородна. Но что было бы, если бы Вселенная не была однородной?
Если Вселенная изотропна, то единственный способ для нее не быть при этом еще и однородной — это иметь структуру в форме своего рода оболочек.

Гипотеза о неоднородной Вселенной. Слева изотропная однородная Вселенная, справа изотропная неоднородная Вселенная. Крест в центре обозначает нас.
Если бы это было так, то в любой другой точке Вселенная бы не выглядела изотропной. То есть, если мы не хотим верить, что каким-то образом мы оказались точно в центре Вселенной, да так, что вся Вселенная имеет сферическую симметрию вокруг нас, то нам придется признать, что Вселенная не только изотропна, но и однородна.
Космологический принцип
Итак, если мы не верим, что находимся точно в центре Вселенной, то Вселенная обязана быть однородной. Однородная Вселенная означает, что Вселенная равномерно заполнена частицами (галактиками) по всему объему. Это называется космологический принцип. Космологический принцип справедлив, потому что наши наблюдения свидетельствуют об этом, разумеется, до некоторой степени аппроксимации.
Некоторые астрономы утверждают, что они наблюдали масштабные неоднородности во Вселенной. Лектор выражает сомнение в надежности этих источников и утверждений.
Конечно, идея об однородности Вселенной не абсолютно точна. Даже тот факт, что существуют галактики, уже говорит о том, что есть неоднородности. Кстати говоря, существуют не только галактики, но и скопления галактик. Однако, на достаточно большом масштабе, приблизительно порядка 1 миллиарда световых лет, Вселенная выглядит однородной.
Сначала космологический принцип был только постулатом. Но с накоплением наблюдательных данных он подтверждался все надежнее, и в конце концов, было открыто реликтовое микроволновое излучение, которое свидетельствует о том, что изначальное распределение материи во Вселенной было в высшей степени однородным.
Постановка физической задачи
Имеется однородный газ из частиц-галактик. И каждая галактика взаимодействует с другими галактиками. Галактики как целое электрически нейтральны. Но они не нейтральны гравитационно. Они взаимодействуют посредством ньютоновской гравитации. И это единственная важная сила на больших масштабах. Гравитация воздействует на галактики и пытается притянуть их все вместе.
Итак, если рассмотреть любую точку во Вселенной и задаться вопросом, куда же она должна двигаться, то можно догадаться, что со всех сторон ее окружает одинаковое количество массы. Следуя этой логике, можно предположить, что никакая галактика не должна двигаться вообще, и Вселенная должна быть статичной, так как результирующая сил, действующих на любую точку во Вселенной, равна нулю. Это абсолютно неверно!
И сейчас мы получим ньютоновские уравнения движения для Вселенной. Вы могли слышать, что расширяющаяся Вселенная хорошо согласуется с общей теорией относительности Эйнштейна, и что до общей теории относительности закон расширяющейся Вселенной был непонятен. Это просто неправда. Возможно, это и было так исторически. Но это лишь исторический факт о датах, а не о логике. Ньютон мог получить уравнения расширяющейся Вселенной. И мы сейчас сделаем это так, как следовало бы сделать Ньютону.
Система координат
В любой физической задаче необходимо первым делом ввести систему координат. Вместо того, чтобы выбирать шаг координатной сетки как расстояние: 1 метр, миллион километров, тысяча световых лет, — мы выберем координатную сетку так, чтобы ее узлы были жестко привязаны к галактикам. Поскольку Вселенная однородна, мы можем это сделать. Тогда галактики будут всегда оставаться примерно в одних и тех же координатах независимо от того, что происходит со Вселенной. То есть, галактики словно «вморожены» в координатную сетку.
Это совсем не очевидно, что можно так сделать. Если бы галактики двигались совершенно случайно и в совершенно разных направлениях, то мы не могли бы этого сделать. Но мы видим, что галактики движутся неслучайно. Мы видим, что галактики движутся согласованно, в точности так, как если бы они были встроены в некую координатную сетку. И то что мы видим, позволяет нам это сделать, потому что скорости галактик относительно друг друга согласованы и неслучайны.
Мы вводим координатную сетку . Эти координаты измеряются не в единицах длины. Если рассмотреть две галактики, разделенные интервалом
, то расстояние
между ними (в метрах) выражается как
где — это масштабный параметр, который может быть константой, а вообще говоря, может и не быть. Масштабный параметр может зависеть от времени
.
Таким образом, по теореме Пифагора расстояние между двумя галактиками в общем случае записывается как
И разумеется, параметр не является константой. Если бы он был константой, то галактики были бы статичны, они бы никуда не двигались. А это не то, что мы наблюдаем. Мы видим, что они разлетаются друг от друга.
Закон Хаббла
Запишем относительную скорость между двумя галактиками. Продифференцируем предыдущую формулу по времени. Учтем то, что — это фиксированный интервал, который не может изменяться по условиям построения системы координат. Тогда
где используем обозначение .
Запишем теперь отношение относительной скорости двух галактик к расстоянию между ними
Отметим, что сокращается, и это соотношение вообще не зависит от координат. То есть данная формула справедлива для любых двух галактик независимо от того, как далеко или близко они находятся.
Это соотношение называется постоянной параметром Хаббла
и оно не зависит от координат. Тогда можно записать то же самое в стандартной форме
Относительная скорость двух галактик пропорциональна расстоянию между ними.
Нужно понимать, что мы бы этого никогда не записали, если бы Хаббл не открыл свой закон. С другой стороны, закон Хаббла не такой уж удивительный. Есть поговорка: «Нет ничего удивительного в том, что самая быстрая лошадь скачет впереди всех.» Чем быстрее вы движетесь, тем дальше вы находитесь. И это факт, который Хаббл и открыл.
Масса вещества во Вселенной
Рассмотрим некоторый объем . Зададим вопрос: какая масса сосредоточена в этом объеме? Пусть
— это масса вещества в элементарном объеме
(в килограммах). Тогда масса в объеме
равна
Каков метрический объем этой области? Так как , можем записать
Какова плотность вещества в этой области? По определению плотность равна , то есть с учетом двух предыдущих формул получим
Это стандартная физическая плотность вещества.
Хотя общее количество массы в объеме не меняется, поскольку галактики «вморожены» в координатную сетку, абсолютная плотность вещества в этом же объеме может изменяться, так как параметр
зависит от времени.
Теорема Ньютона
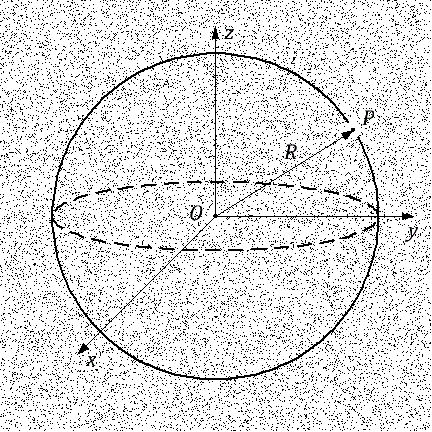
Иллюстрация к теореме Ньютона
Рассмотрим две галактити. Одну из них мы всегда можем поместить в начало координат. Пусть галактика находится в начале координат, а галактика
находится на каком-то удалении от нее.
Теорема Ньютона утверждает, что сила гравитации, действующая на галактику
зависит только от количества массы внутри сферы с центром в начале координат
, и проходящей через галактику
. Второе утверждение теоремы Ньютона состоит в том, что всю массу внутри этой сферы можно считать сосредоточенной в центре в начале координат в точке
, при условии что масса внутри сферы распределена если не однородно, то по крайней мере изотропно.
Иными словами, действие всей массы внутри сферы на галактику эквиваленто тому, как если бы эта масса была сосредоточена в одной единственной точке
, которая является центром сферы.
Ньютоновские уравнения движения
Найдем расстояние между галактиками и
. Галактика
имеет координаты
, то есть расстояние из центра до галактики
равно
Можем ввести обозначение
измеряется не в метрах, а в тех же единицах, что
,
и
и не зависит от времени. Тогда
Запишем теперь скорость и ускорение галактики
Теперь мы должны приравнять ускорение к ускорению связанному со всей гравитирующей массой внутри сферы радиуса
. Обозначим массу галактики
за
, а массу всего вещества внутри сферы за
. Тогда сила гравитации, действующая на галактику
равна
где — гравитационная постоянная. Знак минус в формуле означает, что это сила притяжения.
Теперь можно записать ускорение галактики
Приравниваем два выражения для и получаем
Учтем, что , тогда
Поделим обе части на
Найдем объем сферы
Домножим числитель и знаменатель правой части на
Это уравнение не зависит от , и оно справедливо для любой галактики во Вселенной. Это уравнение — центральное фундаментальное уравнение космологии.
Одно из следствий этого уравнения это то, что невозможно, чтобы Вселенная была статичной, если она не пустая. Из этого уравнения следует, что Вселенная может быть статичной только если она пустая.
Мы можем переписать это уравнение, учитывая что
Это уравнение было впервые получено в контексте общей теории относительности Александром Фридманом. Это уравнение не сообщает нам о том, расширяется ли Вселенная или сжимается. Оно только говорит о том, что вторая производная масштабного фактора отрицательная. То есть если Вселенная расширяется, то она замедляется, а если Вселенная сжимается, то она ускоряется.
На самом деле Вселенная расширяется и не замедляется. Мы лишь только сделали то, что мог бы сделать Ньютон и что все Космологи считали правильным вплоть до примерно 1998 года. Эта модель была общепринятой и называлась стандартной моделью Вселенной до тех пор, пока не было открыто ускоряющееся расширение Вселенной. Пока что в правой части уравнения только одно слагаемое. На самом деле там должно быть несколько слагаемых, которые связаны с общей теорией относительности.
Скорость вылета
Теперь запишем полную энергию галактики как сумму кинетической и потенциальной
Энергия может быть положительно либо отрицательной в зависимости от соотношения между этими двумя слагаемыми. Важно помнить также, что полная энергия частицы сохраняется. Если полная энергия положительна, то частица не может повернуть назад. Частица поворачивает назда, только когда полная энергия отрицательна. Граничный случай — это полная энергия равна нулю. Решим уравнение
для
чтобы найти скорость вылета.
Точно так же как и галактика вся Вселенная может иметь скорость выше скорости вылета, меньше скорости вылета либо равную скорости вылета. Если скорость Вселенной выше скорости вылета, то она расширяется и никогда не начинает сжиматься, если же Вселенная имеет скорость ниже скорости вылета, то рано или поздно начнет сжиматься.
Перепишем уравнение полной энергии
Уравнение Фридмана
Рассмотрим случай, когда скорость Вселенной совпадает со скоростью вылета.
Упростим выражение: поделим, на , домножим на 2, поделим на
Во втором слагаемом домножим числитель и знаменатель на . Тогда в знаменателе получим метрический объем сферы
. Учитывая, что
, получаем
Это называется уравнением Фридмана. Оно эквивалентно ньютоновскому уравнению, полученному выше. Поскольку мы предположили, что полная энергия равна нулю, то такая Вселенная расширяется, замедляясь асимптотически до нуля, но никогда не пересекает ноль и не начинает сжиматься.
Вспомним теперь что . Перепишем уравнение Фридмана
Параметр очень гибкий. Он полностью зависит от нашего выбора координатной сетки. И, вообще говоря, мы могли бы даже выбрать его так чтобы
. Тогда
Правая часть этого уравнения всегда положительна, а следовательно, скорость расширения никогда не становится равной нулю. Вспомним теперь, что
— это постоянная параметр Хаббла. Из уравнения также следует, что параметр Хаббла никогда не изменяет знак. Однако, он все же замедляется. Параметр Хаббла становится все меньше и меньше со временем.
Это уравнение чрезвычайно важно для всей космологии. Простой способ решить его — это искать решение определенного вида, а именно, мы будем искать решение в форме
где и
— некоторые константы.
Мы получили решение уравнения Фридмана.
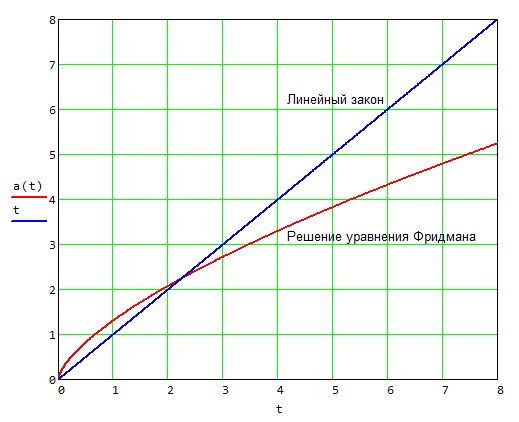
График решения уравнения Фридмана
Реальная Вселенная следует этому решению лишь до некоторого момента времени, а затем начинает ускоряться. Ньютон мог это сделать. Он подошел очень близко. Задал все правильные вопросы. Лектор выражает уверенность, что Ньютон, вполне вероятно, это сделал и получил данное решение. Однако такие сведения о Вселенной шли вразрез с его религиозными взглядами, и поэтому он не стал публиковать свои открытия.
