Контекстные многорукие бандиты для рекомендации контента, или Не Бернулли единым30.06.2022 19:17

Привет, Хабр! Меня зовут Александр Сухочев, я занимаюсь машинным обучением и руковожу командой рекомендаций и развития сервисов ВКонтакте. Сегодня хочу поделиться нашим опытом и результатами внедрения контекстных многоруких бандитов для рекомендации контента на примере игр и стикеров.

Статья состоит из четырёх частей, переходите сразу ко второй или третьей, если знакомы с проблематикой, или читайте по порядку, чтобы составить полную картину:

Введение

Верхнеуровнево обычная рекомендательная система выглядит следующим образом:

Что не так с «классическими» ML-рекомендациями?

Рекомендации, основанные только на опыте предыдущего взаимодействия пользователей с контентом и не байесовском частотном подходе к обучению (например, различные алгоритмы, основанные на матричных факторизациях, бустингах и т. д.), могут быть качественными, но есть недостатки, с которыми в рамках данных подходов сложно бороться:

Алгоритмы учатся на истории, на формирование которой сами же и повлияли. Однако этот факт нигде не учитывается и может приводить к нежелательным смещениям в обучении.
Усложняется поиск ниши для потенциально качественного, но самобытного контента.
В рекомендациях в основном показывается контент на темы, которые когда-то интересовали пользователя, а новые темы платформа не предлагает.
Непонятно, что делать с перманентным появлением на платформе нового контента, который потенциально может быть качественным и достойным большой аудитории. Крайним случаем является запуск новой платформы рекомендаций или появление на сайте нового типа контента. Тогда в нашем распоряжении вообще нет никакой истории взаимодействия, на которой можно учиться.

Все они требуют решения, но последние три могут особенно повлиять на отношение пользователей к сервису. Мы точно не хотим тратить время и нервы пользователей на новый и не обязательно качественный и (или) подходящий им контент.

В литературе такая проблема называется exploitation-exploration trade-off:

с одной стороны, мы хотим получить пользу от рекомендательной системы, применяя уже имеющиеся знания — это exploitation;
с другой стороны, действуя таким «жадным» образом, мы будем медленно получать новые знания, которые потенциально могли бы помочь нам извлекать ещё больше пользы в будущем. Поэтому хотелось бы иногда рисковать и пробовать новые паттерны поведения, предлагать новый контент или рекомендовать контент нестандартной для него группе пользователей — это exploration.

Что за бандиты такие, многорукие?

В машинном обучении задача о многоруком бандите — это задача о грамотном комбинировании exploration и exploitation. Своё название она получила из-за сходства с игрой в казино:

игрок приходит в казино со слот-машинами (также известными как однорукие бандиты) и, естественно, хочет выиграть как можно больше;
слот-машина с некоторой вероятностью выдаёт фиксированный выигрыш на каждую попытку игрока дёрнуть за ручку автомата, но у каждого однорукого бандита своя вероятность выигрыша;
достоверно известно, что есть однорукий бандит с вероятностью получения выигрыша, ради которой есть смысл его искать;
таким образом, цель игрока — как можно быстрее найти наиболее выгодного однорукого бандита и играть в него.

Так обычно выглядят слот-машины в реальной жизни, отличие только в том, что в нашем случае ответ не состоит из трёх картинок, которые в комбинации дают те или иные значения выигрыша, а является бинарной величиной (выиграл фиксированную сумму или нет)

Так как одноруких бандитов много, то обычно говорят, что мы имеем дело с одним многоруким бандитом, каждой ручкой которого является ручка однорукого бандита.

В прикладных задачах каждая ручка многорукого бандита представляет собой не выбор очередной слот-машины, а выбор действия из какого-то дискретного множества действий, которое должно максимизировать бизнес-метрику. Действия и метрики разнятся в зависимости от области и задачи. Например, в рекомендациях действием может быть как показ пользователю какой-то конкретной единицы контента, так и выбор верхнеуровневого принципа, по которому мы в данный момент будем генерировать рекомендации для пользователя.

Задача состоит в том, чтобы как можно быстрее идентифицировать эффективную стратегию и затем придерживаться её.

Основные алгоритмы решения задачи о многоруком бандите

Чтобы разобрать алгоритмы, сначала формализуем задачу. Существуют разные модели, но в общем случае задачу о многоруких бандитах можно изобразить в виде схемы:

Принцип задачи о многоруком бандите (схема позаимствована из web.stanford.edu/~bvr/pubs/TS_Tutorial.pdf) Принцип задачи о многоруком бандите (схема позаимствована из web.stanford.edu/~bvr/pubs/TS_Tutorial.pdf)

Есть агент (online decision algorithm), среда (system) и потенциально бесконечная последовательность итераций взаимодействия агента и среды, пронумерованная индексом t. На каждом t-ом шаге агент принимает решение совершить действие a_t , среда в ответ на это действие выдаёт ответ y_t , который напрямую или опосредованно через функцию r(y) характеризует выигрыш агента.

В общем случае сигнал y_t носит стохастический (недетерминированный) характер. Можно говорить, что действие агента a_t на t-ом шаге задаёт вероятностное распределение на ответ $\mathbb{Y}_t$ , из которого конкретная реализация ответа y_t получается случайным сэмплированием (то есть берутся частные реализации случайной величины). Далее на основе вновь совершённого действия a_t и полученного сигнала y_t мы обновляем приближения $\hat{\theta}$ параметров $\theta$ модели зависимости ответов среды от совершённых действий (блок supervised learning на диаграмме). В дальнейшем ради краткости будем этот элемент называть моделью среды. Далее на основе очередных приближений алгоритм принятия решения о совершении тех или иных действий (optimizer) выдаёт следующий шаг $a_{t+1}$ , который нужно совершить. Так выглядит каждая итерация взаимодействия агента со средой.

Задача о казино является, пожалуй, одним из простейших примеров задачи о многоруком бандите, а именно — задачей о бернуллиевском многоруком бандите. В этой задаче модель зависимости ответов среды от совершённых действий представляет собой набор из K распределений Бернулли: по одному распределению на ручку $a_k, k \in \{1,...,K\}$ . Каждое k-ое распределение Бернулли представляет собой распределение случайной величины, которая может принимать значение, равное единице (выигрыш) с вероятностью $\theta_k$ и нулю (проигрыш) с вероятностью $1 - \theta_k$ . Набор таких $\theta_k , k \in \{1,...,K\}$ и является параметрами данной модели.

Несмотря на простоту, с помощью такой модели можно решать прикладные задачи, и на её примере мы разберём основные подходы к решению задачи о многоруком бандите. Далее обозначим её недостатки и возможные усложнения, которые позволяют от них избавиться.

Эпсилон-жадный подход

Самым простым подходом является эпсилон-жадный алгоритм. В общем виде он работает следующим образом:

мы с вероятностью $\varepsilon$ выбираем ручку бандита, у которой на основе уже полученных данных наибольший средний выигрыш, а с вероятностью $1-\varepsilon$ — случайную ручку;
обновляем математические ожидания выигрыша у всех ручек;
повторяем с первого пункта.

К задаче бернуллиевских бандитов этот подход применяется тривиальным образом:

для каждой ручки считаем отношение количества выигрышей к количеству попыток;
с вероятностью $\varepsilon$ пробуем ручку с максимальным отношением — это exploitation, а с вероятностью $1-\varepsilon$ пробуем случайную ручку — и реализуем exploration;
получая новые данные, обновляем отношения.

Недостаток этого подхода состоит в нерациональном exploration. По мере поступления данных нам становится понятно, что какие-то ручки более перспективны для исследования, чем другие. Однако они всё равно получают одинаковые шансы быть рекомендованными пользователю на очередной итерации exploration.

Для наглядности давайте представим, что хотим рекомендовать фотографии кошек.

По прошествии какого-то времени мы собрали следующие данные: первая набрала 2 000 лайков и 100 000 просмотров, вторая ни одного лайка и всего 10 просмотров, третья — 1 лайк и 10 000 просмотров. Лайки мы здесь считаем за те самые выигрыши, а просмотры за попытки.

На стадии exploitation будет выбран первый кот — как наиболее перспективный на основе текущей информации.

Теперь поговорим про exploration. Вторая фотография набрала меньше лайков как в абсолютных величинах, так и в отношении к количеству просмотров, чем третья. Однако на основе количества этих самых просмотров мы можем выдвинуть предположение, что исследование востребованности второй фотографии более перспективно, а невостребованность третьей для рекомендаций уже весьма вероятна. При эпсилон-жадном подходе обе картинки будут получать одинаковые шансы быть рекомендованными пользователю на этапе exploration.

Конечно, с такой неоптимальностью можно попробовать побороться различными эвристиками, вроде условий на количество просмотров и отношение количества выигрышей к количеству попыток. Но это ненадёжно.

Байесовский теоретический минимум

Для дальнейшего рассмотрения принципов работы многоруких бандитов нам нужен способ обучения моделей, который позволит:

В потоковом режиме (то есть без сохранения обучающей выборки в памяти и постоянного её переиспользования) комбинировать новые данные с уже имеющимися у нас представлениями о среде, получая новую, более точную модель среды.
Получать не просто точечные оценки параметров модели, но и их вероятностное распределение, которое ещё и помогает понять, насколько мы уверены в текущих оценках.

Этим требованиям удовлетворяет байесовский подход. Весь его смысл можно выразить одной небольшой формулой — собственно формулой Байеса:

$P(B|A) = \frac{P(A|B)P(B)}{\int P(A|B)P(B)dB}$

Чтобы разговор был более предметным, сразу вместо абстрактных A и B подставим актуальные для машинного обучения с учителем понятия A = Y|X (ответы модели при условии факторов) и $B = \theta$ (параметры модели машинного обучения). Получим:

$p(\theta|Y, X) = \frac { p(Y|\theta, X) \cdot p(\theta) } { \int p(Y|\theta, X) p(\theta) d \theta },$

где $p(\theta)$ — текущие представления о модели, выраженные в виде плотности распределения параметров этой модели и построенные на основе предыдущих данных и базовых априорных представлений (либо только априорных представлений, если данных ещё не было). Этот множитель в литературе называется априорным распределением.

$p(Y|\theta, X)$ несёт в себе информацию о вновь полученных данных в виде их функции правдоподобия. Этот множитель так и называется в литературе — правдоподобие.

$p(\theta|Y, X)$ — наши обновлённые представления о модели, полученные на основе старой модели и новых данных. В литературе этот множитель называется апостериорным распределением.

Сомножитель $\frac{1}{\int p(Y|\theta, X) p(\theta) d \theta}$ нужен для нормализации.

Если его убрать, то $p(Y|\theta, X) \cdot p(\theta)$ нельзя рассматривать как плотность распределения параметров, так как интеграл по ней не будет суммироваться в единицу.

Иногда нормализующий множитель удаётся вычислить аналитически, в этом случае будем говорить, что проводим байесовский вывод. Однако, за исключением простейших случаев, вычислить его аналитически крайне сложно или попросту невозможно. Численное же вычисление может быть весьма трудоёмким и тогда пытаются приблизить апостериорное распределение $p(\theta|X)$ каким-нибудь распределением $q(\theta)$ , с которым удобнее работать: оценивать плотность, брать сэмплы, избегая затруднительных подсчётов нормализующих констант. Этот подход называется приближённым вариационным выводом.

На практике используются оба эти способа, их применение мы и рассмотрим в дальнейшем в этой статье. Также возможно использовать Марковские цепи и метод Монте-Карло, но в многоруких бандитах их используют очень редко, поэтому на них останавливаться не будем.

Рассмотрим, как выводится апостериорное распределение в задаче бернуллиевских бандитов посредством аналитического подсчёта нормализующей константы, то есть проведем байесовский вывод. Здесь у нас нет никаких факторов, описывающих контекст, поэтому вместо Y|X рассмотрим просто Y.

Напомню, что параметр $\theta$ — это совокупность параметров $\theta_k$ , каждый из которых в данном случае обозначает вероятность получить награду при использовании k-ой ручки и таким образом задаёт следующую плотность распределения данных:

$p(Y_k| \theta_k) = \prod_i p(y_{ki}|\theta_k) = \prod_i \big( \theta_k^{[y_{ki} = 1]} \cdot (1 - \theta_k)^{[y_{ki} = 0]} \big) \\= \theta_k ^ {\sum_i [y_{ki} = 1]} \cdot (1 - \theta_k) ^ {\sum_i [y_{ki} = 0]}.$

Здесь Y_k — ответы только на попытках использовать k-ую ручку; $y_{ki}$ — ответ на i-ой итерации использования k-ой ручки; [x] — это функция, принимающая значение 1, когда истинно, и 0, когда ложно.

За априорное распределение уже самих параметров $\theta_k$ возьмём бета-распределение:

$p(\theta_k) = \frac{\theta_k ^ {\alpha_k - 1} \cdot (1 - \theta_k) ^ {\beta_k - 1}}{B(\alpha_k, \beta_k)}.$

Здесь $\alpha_k$ и $\beta_k$ — параметры k-ого бета-распределения (то есть параметры распределения параметра $\theta_k$ ). $B(\alpha, \beta)$ — бета-функция, конкретный вид которой в данном случае не важен.

Среди всех семейств распределений мы выбрали именно семейство бета-распределений, потому что:

оно задаёт распределение величины на отрезке от 0 до 1 (а $\theta$ как раз может принимать только значения из данного отрезка);
если использовать такое априорное распределение, то апостериорное распределение вычисляется аналитически (покажу далее).

Виды бета-распределения при различных значениях параметров, картинка из Википедии Виды бета-распределения при различных значениях параметров, картинка из Википедии

Обновление апостериорного распределения при поступлении новых данных проводится очень просто, на самом деле апостериорное распределение, как и априорное, здесь является бета-распределением и имеет параметры

$\alpha^{new}_k=\sum_i [y_{ki} = 1] + \alpha_k\ \text{и}\ \beta^{new}_k= \sum_i [y_{ki} = 0] + \beta_k.$

То есть апостериорное распределение вычисляется аналитически и поэтому крайне быстро.

Краткое доказательство этого факта.

Замечание. В случае, если априорное и апостериорное распределения принадлежат одному семейству, как здесь, говорят, что априорное распределение сопряжено распределению правдоподобия. С такими парами сопряжённых распределений, как было показано выше, легко работать, но часто бывает сложно подобрать априорное распределение, которое было бы сопряжено правдоподобию.

Сэмплирование Томпсона

В общем виде сэмплирование Томпсона работает следующим образом:

из текущего апостериорного распределения параметров среды $\theta$ сэмплируем их значения;
считая результаты сэмплирования за истинные значения параметров среды, выбираем действие, при котором математическое ожидание выигрыша наибольшее;
получив новые данные, пересчитываем обновлённое апостериорное распределение параметров $\theta$ , считая предыдущее апостериорное распределение за априорное;
повторяем всё с первого пункта.

Применительно к задаче бернуллиевских бандитов этот алгоритм выглядит следующим образом. Среда описывается набором параметров $\theta_k$ (по одному на каждую k-ую ручку), каждый такой параметр имеет априорное бета-распределение. На каждой итерации мы:

из каждого бета-распределения параметров $\theta_k$ наших ручек сэмплируем их значение $\Theta_k \sim p(\theta_k)$ ;
просэмплированные значения $\Theta_k$ считаем за вероятность той или иной ручки принести выигрыш, таким образом, оптимальным действием является $\arg\max_k \Theta_k$ ;
получив новую информацию от среды в ответ на наши действия, пересчитываем значения бета-распределения параметров по схеме, описанной выше;
повторяем всё с первого пункта.

Сэмплирование Томпсона реализует гораздо более грамотную стратегию exploration-exploitation trade-off. Интуитивно её можно понять так: когда мы сэмплируем $\Theta_k$ из распределений $p(\theta_k)$ , то наибольшие значения получаются либо из распределений с большим математическим ожиданием (в этом случае мы ближе к exploitation), либо из распределений с большой дисперсией (в этом случае мы ближе к exploration).

Если объяснять на котах, то в ситуации, описанной выше, при подобном подходе скорее всего будут выбраны:

Третья же картинка будет иметь весьма небольшие шансы быть выбранной, так как у неё и небольшое математическое ожидание $\frac{2}{2 + 10000} \approx 0,0002,$

и небольшая дисперсия $\frac {2 * 10000}{(2 + 10000)^2 (2 + 10000 + 1)} \approx = 0,00000002.$

В статьях же алгоритмы принятия решений, частным случаем которых является задача о многоруком бандите, обычно оцениваются с помощью

$Regret(T) = \sum_{t=1}^{T} \Big( E(y_t|a^*) - E(y_t|a_t)\Big),$

где T — число итераций принятия решений, t — номер итерации, E(y_t|a^*) — математическое ожидание случайной величины y_t при условии совершения оптимального действия a^* , $E(y_t|a_{t})$ — математическое ожидание случайной величины y_t при условии совершённого нашим алгоритмом действия $a_{t}$ .

Например, в этой работе эмпирически на множестве примеров проведено сравнение сэмплирования Томпсона с эпсилон-жадным алгоритмом с использованием Regret .

Upper Confidence Bound

Ещё одним популярным алгоритмом решения задачи о многоруком бандите является алгоритм Upper Confidence Bound (UCB). Кратко его смысл состоит в том, чтобы на каждом этапе выбирать ручку с наибольшей взвешенной суммой математического ожидания выигрыша и слагаемого, отвечающего за неуверенность прогноза.

$a_t = \arg\max_{a_t} expected\_return + w \cdot uncertainty$

Такой принцип выбора действий на каждом шаге интуитивно похож на принцип в сэмплировании Томпсона. Для UCB-алгоритма есть теоретические оценки производительности (regret), но более подробно мы его разбирать не будем, так как на практике в условиях побатчевого обновления параметров среды и генерации контента алгоритм сэмплирования Томпсона позволил нам проводить больший exploration.

Алгоритм контекстных многоруких бандитов

На практике редко одно действие лучше другого при любом раскладе, обычно очень многое зависит от контекста. В рекомендательных системах таким контекстом, который необходимо учитывать, обычно являются признаки пользователя.

Наивный подход

Самый простой способ учесть контекст — разделить признаковое пространство пользователя на отдельные ячейки разбиением по значениям признаков и считать «бандитские» статистики в каждой такой ячейке.

Ниже на иллюстрации пространство пользователя нарезано на ячейки, в которые помещаются те случаи взаимодействия пользователя с контентом, когда пользователь имел признаковое описание, соответствующее данной ячейке.

Кружки обозначают взаимодействия пользователя с контентом в истории. Для простоты берём пока только два фактора: пол и возраст.

Далее в каждой ячейке независимо от других на основе данных пересчитывается свой набор из k бета-распределений параметров $\theta_k$ . Можно сказать и наоборот: для каждой ручки мы считаем M бета-распределений, где M — количество ячеек.

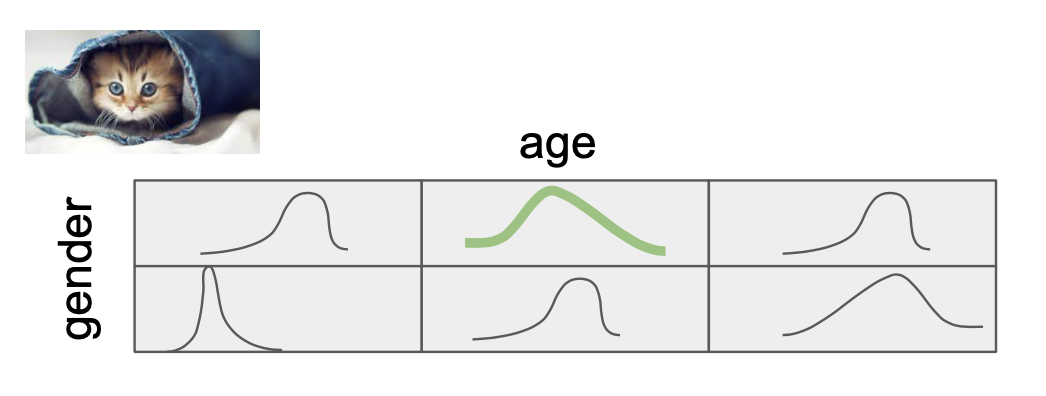
Таким образом, вместо K распределений в случае, когда мы не учитываем контекст, нам приходится рассматривать и пересчитывать K*M распределений.

Этот подход имеет несколько недостатков:

непонятно, как корректно разбивать пространство по признакам
(в примере выше разбиение по возрасту можно сделать экспертно или на основе принятой классификации, но если добавить, например, тематические описания пользователя, то задача станет сложнее);
когда мы увеличиваем количество учитываемых признаков, мы бьём пространство на большее количество ячеек и в каждой ячейке остаётся меньше прецедентов для обучения.

Логистическая регрессия + вариационный вывод

Пришло время глобально поменять модель среды. Если раньше вероятность бинарного выигрыша при использовании k-ой ручки зависела от одного параметра $\theta_k$ , то сейчас мы вводим для каждой ручки вектор параметров $\theta_k = (\theta_k^1, ..., \theta_k^v)$ . Пусть контекст характеризуется вектором признаков x = (x^1, ..., x^v) , тогда вероятность выиграть при использовании k-ой ручки будет равна

$\sigma(\theta_k^T \cdot x) = \frac{1}{1 + e^{-\theta_k^T \cdot x}},$

где сигмоида гарантирует, что значение, которое мы получаем от модели будет между 0 и 1.

Правдоподобие для каждой k-ой ручки будет считаться также отдельно и будет выглядеть как:

$p(Y_k|\theta_k, X_k) = \prod_i \sigma( \theta_k^T \cdot x_{ki})^{y_{ki}} \cdot (1 - \sigma( \theta_k^T \cdot x_{ki}))^{1 - y_{ki}}.$

Здесь Y_k — ответы только на попытках использовать k-ую ручку, $y_{ki}$ — ответ на i-ой итерации использования k-ой ручки, $x_{ki}$ — контекст на i-ой итерации использования k-ой ручки.

В данном случае уже сложно подобрать априорное распределение, которое бы сопрягалось с распределением правдоподобия и позволяло аналитически вычислять апостериорное распределение.

Поэтому в качестве априорного распределения возьмём просто самое популярное — многомерное нормальное распределение:

$p(\theta_k) = Normal(\theta_k|\mu_k, \Sigma_k) = \det(2 \pi \Sigma_k )^{-\frac{1}{2}} \exp\big(-\frac{1}{2}(\theta_k - \mu_k)^T \Sigma_k^{-1}(\theta_k - \mu_k)\big),$

а апостериорное распределение получим с помощью приближённого вариационного вывода, а именно аппроксимации Лапласа.

Этот подход состоит в том, что если мы имеем дело с унимодальным дважды дифференцируемым распределением, в котором весомая часть вероятностной массы сосредоточена вокруг моды, то может быть разумно такое распределение приблизить нормальным распределением.

Математическим ожиданием этого приближения будет мода апостериорного распределения, которую можно легко найти любым алгоритмом оптимизации: $\mu\_new_k = \theta_k^*$ , где $\theta_k^* = \arg\max_{\theta_k} p(Y_k|\theta_k, X_k)p(\theta_k).$

Ковариационная матрица приближённого апостериорного распределения находится по формуле:

$\Sigma\_new_k = \bigg(- \Big(\log\big(p(Y_k|\theta^*_k, X_k)p(\theta^*_k)\big)\Big)''\bigg)^{-1}$

Вывод формул под спойлером.

Hidden text

Заметки о практической реализации и наши результаты

Мы применили метод многоруких контекстных бандитов с лапласовской аппроксимацией и сэмплированием Томпсона для продвижения игр и стикеров на второй вкладке.

В обеих задачах ручками многоруких бандитов были рекомендуемые объекты.

Контекст принятия решений

Контекстом были признаки пользователя: пол, возраст и признаки интересов.

Остановимся подробнее на интересах. Они, с одной стороны, крайне важны, так как наиболее явно характеризуют пользователя, с другой — есть определённые ограничения на их применение.

Во-первых, признаки должны быть довольно небольшими по размеру, потому что в формуле пересчёта $\Sigma$ нужно инвертировать матрицу с длиной стороны, равной количеству признаков. Во-вторых, темы в этих признаках должны быть закодированы в явном виде, без всяких запутанностей, которые свойственны эмбеддингам, потому что далее они подаются на вход не нейронной сети, а обычной логистической регрессии.

Как вариант, можно проводить тематическое моделирование пользователя, в котором пользователь является документом, а группы, на которые он подписан, словами. Но мы избрали другой подход.

Дело в том, что у нас в распоряжении были качественные эмбеддинги сообществ, полученные в ходе решения задачи их рекомендаций и хорошо описывающие их тематику. Мы кластеризовали сообщества в этом пространстве эмбеддингов с помощью адаптивного EM-алгоритма с ограничением на количество кластеров. Получились достаточно хорошо интерпретируемые кластеры. Например, ниже представлены примеры из кластера про IT и популярную науку.

Далее мы разложили пользователя по принадлежности к кластерам групп и это разложение использовали как признаки интересов пользователя.

Что считать положительными и отрицательными взаимодействиями?

Рекомендации стикеров и игр в мобильных приложениях показываются пользователю в виде горизонтального скролл-виджета на вкладке «Сервисы».

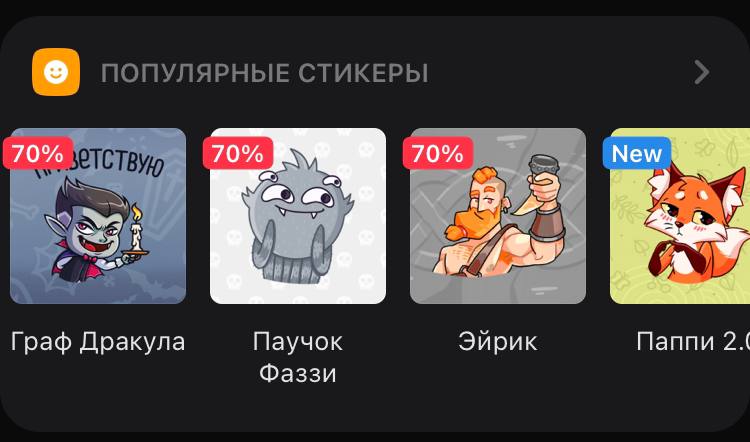
Если дело касается стикеров, то кандидаты на положительный сигнал — это просмотр всех стикеров в наборе и покупка набора.

Для игр положительным сигналом можно считать тап по игре с последующим проведением в ней какого-то значимого времени (чтобы убирать кликбейт или мисклики) и добавление этой игры в любимые.

С отрицательными сигналами всё интереснее, так как явно пользователь их обычно не даёт. Но считать неудачными просто все рекомендации, с которыми пользователь не провзаимодействовал, не стоит, потому что он мог их просто не заметить (тем более это легко в скролл-виджете, в котором изначально не показываются все объекты).

Мы решили считать, что взаимодействие носило отрицательный характер в том случае, когда пользователь точно увидел рекомендуемый объект и при этом сознательно не проявил к нему интереса. Для этого в качестве примеров отрицательного взаимодействия мы берём все объекты в горизонтальных скролл-виджетах, которые расположены слева от объекта, нажатого пользователем. На рисунке ниже такими примерами отрицательных взаимодействий являются «Граф Дракула» и «Эйрик».

Разная значимость сигналов

Естественно, не все положительные действия равнозначны: просмотр набора стикеров и его покупка — не одно и то же. При этом отрицательные взаимодействия в нашей постановке дают не такой явный сигнал, как положительные. Хотелось бы учитывать и те, и другие действия и желательно в рамках одной модели. Мы решили эту задачу назначением весов определённым видам сигналов. В формуле правдоподобия множители возводятся в степень, равную весу соответствующего сигнала:

$p(Y_k|w_k, \theta_k, X_k) = \prod_i \sigma( \theta_k^T \cdot x_{ki})^{w_{ki} \cdot y_{ki}} \cdot \big(1 - \sigma( \theta_k^T \cdot x_{ki})\big)^{w_{ki} \cdot (1 - y_{ki})}$

Квазислучайное сэмплирование

Эксперименты показали, что новые объекты до равноправного участия в сэмплировании Томпсона стоит сначала порекомендовать квазислучайно.

Это значит, что мы не просто случайно выбираем момент, когда поместить в рекомендации новый объект, а делаем это таким образом, чтобы он был порекомендован в как можно более разнообразных контекстах. Это позволяет лучше понять, где этот объект будет впоследствии более востребованным, и обеспечить ему хороший старт.

Существует много способов квазислучайного сэмплирования. Самым популярным, пожалуй, является квазислучайное сэмплирование на основе последовательности Соболя. Мы же используем самописный сэмплер.

Результаты

Первым делом мы протестировали алгоритм на играх на Android. Сравнивали качество классических ML-рекомендаций с подмешанными «бандитскими» рекомендациями против чистых классических ML-рекомендаций с помощью A/B-теста.

Сначала метрики в тестовой группе незначительно упали относительно контроля, но через две недели начали уверенно расти. Через два месяца эффект составил +8% установок игр, +2% запусков, после чего мы раскатили новые рекомендации на всю аудиторию. Результаты на стикерах против классических ML-рекомендаций дали +5% к выручке от их продажи.

В обоих случаях большее количество объектов — игр и стикеров — начали получать внимание пользователей.

Сейчас внедряем этот подход в рекомендации других сущностей, а также разрабатываем новые подходы для случаев, когда фидбэк приходит не сразу (reinforcement learning решения) и когда мы всё-таки хотим не ограничиваться небольшим количеством факторов, а использовать всю доступную информацию по максимуму (deep learning модификации наподобие описанной в этой статье).

У нас много разных ML-проектов, они интересные, сложные и высоконагруженные. И если при мысли о возможности учить свои reinforcement learning алгоритмы в реальном врем