Комплексные числа и геометрические узоры06.07.2021 12:31

Когда речь заходит о комплексных числах, в первую очередь вспоминают о преобразовании Фурье и прочих аспектах цифровой обработки сигналов. Однако у них есть и более наглядная интерпретация, геометрическая — как точки на плоскости, координатам которой соответствуют действительная и мнимая часть комплексного числа. Рассматривая некоторую кривую как совокупность таких точек, можно описать её как комплексную функцию действительной переменной.

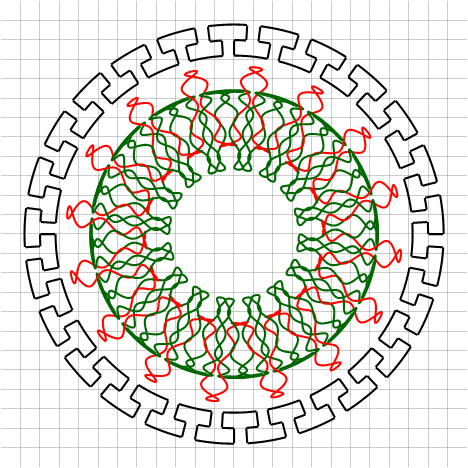
▍ Окружность

Когда нам нужно начертить окружность в реальной жизни — мы берём циркуль и, уперев его одним (острым) концом, а другим (с грифелем) постепенно вращая, оставляем след на бумаге. В математике это делается аналогично — в роли циркуля выступает мнимая единица $i$

, а в роли вращения — возведение её в степень переменной $t$

, которую можно интерпретировать как момент времени (а в данном конкретном случае — как угол поворота). Здесь вектор описывает полный круг при изменении значения $t$

от

до

— что также удобно интерпретировать как четверти на координатной плоскости, когда при изменении целой части $t$

одна из проекций на координатную ось меняет свой знак.

$f(t)=i^t$

Возможно, выражение $i^t$ кому-то может показаться несколько непривычным, поскольку оно не употребляется в традиционных учебниках математики. В таком случае можно использовать каноническую запись, перейдя к основанию $e$ : $i^t = e^{\frac{i \pi t}{2}}$ .

Также в качестве основания можно использовать минус единицу: $i^t=(-1)^{t/2}$ , что часто используется в Wolfram Mathematica для описания единичных комплексных констант.

Разница между функциями $e^{i t}$ , $(-1)^t$ и $ i^t$ состоит лишь в периоде $t$ для полного оборота вектора по окружности — $2 \pi$ , $2$ или $4$ . Запись с экспонентой является исторически первой, однако её сложно назвать наглядной — возведение в комплексную степень несколько контринтуитивно. В этой же статье вариант $ i^t$ выбран по причине его большей компактности и наглядности.

▍ Эллипс

Эллипс можно начертить растягиванием окружности вдоль одной из осей. Но в таком случае это получится самый обычный параметрический график с участием тригонометрических функций, но без участия комплексных чисел. В комплексных же числах эллипс можно представить как сумму двух векторов разной длины и вращающихся с одной частотой, но в противоположные стороны:

$f(t) = i^{-t}+3 i^t$

Поскольку в комплексных числах результат суммы тоже не зависит от порядка слагаемых, эту же анимацию можно представить чуть по-другому:

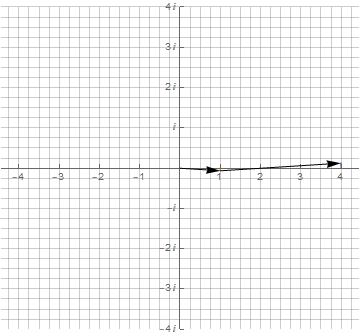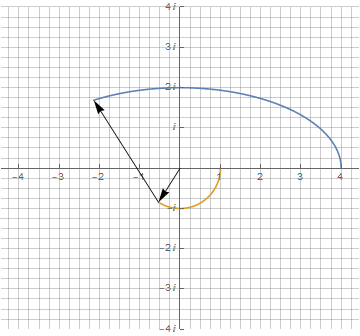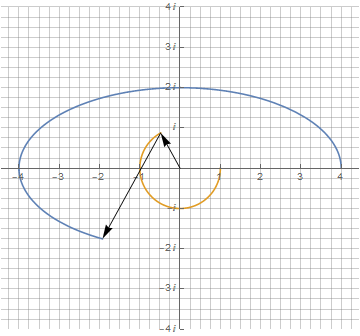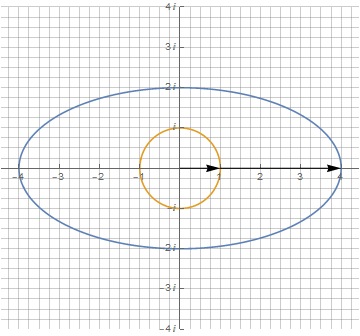
Используя формулу в полярных координатах, можно начертить эллипс одним вектором, но с динамически изменяемой длиной:

$f(t)=i^t \sqrt{\frac{2 a^2 b^2}{\left(b^2-a^2\right) \cos \left(\frac{2 \pi t}{2}\right)+a^2+b^2}},a\to4,b\to2$

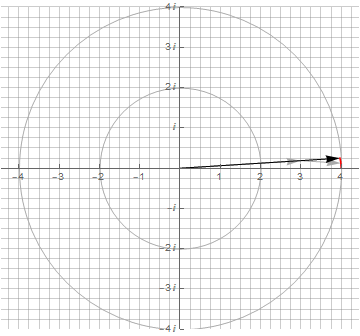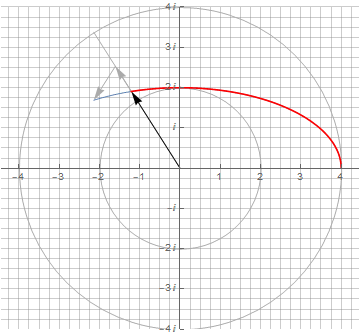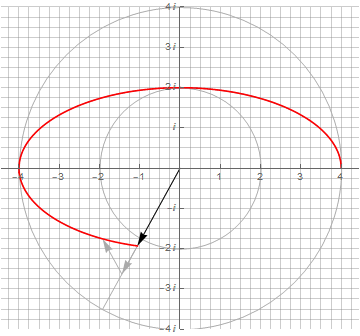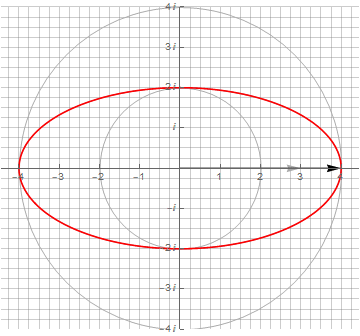
Несмотря на то, что фигуры получаются одинаковыми, положение точки (и скорость) в каждый момент времени не совпадают, что хорошо видно на анимации. Поэтому производные этих эллипсов совпадать не будут:

формулы производных

Примечательно, что производная от эллипса, задаваемого суммой двух векторов, осталась тем же эллипсом с теми же пропорциями. Ну, а теперь — самое главное преимущество комплексных чисел: чтобы повернуть эллипс на произвольный угол, достаточно просто умножить его на единичный вектор с необходимым углом поворота (phi):

$f(t)=i^{\text{phi}} \left(i^{-t}+3 i^t\right)$

▍ Гипотрохоида и прочее

Усложнение получаемых фигур достигается усложнением их мат.модели. Достаточно изменить частоту второго вектора, и можно получить нечто более интересное, а именно — математическую модель спирографа:

$f(t) = i^{-t}+3 i^{t/3}$

$f(t)=i^{-t}+3 i^{\frac{3 t}{4}}$

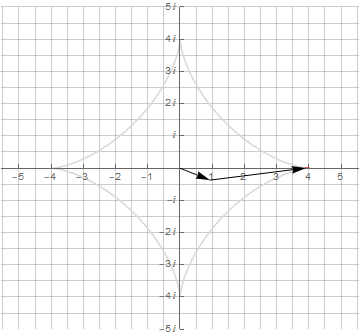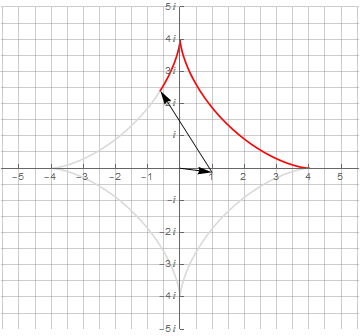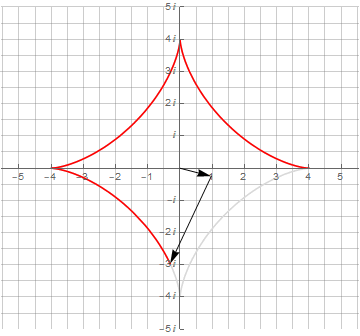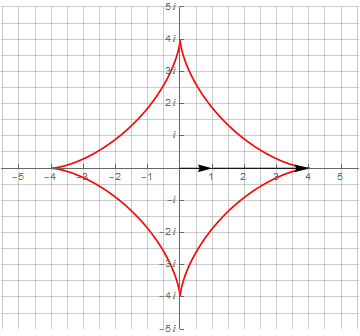
Здесь необходимо обратить внимание на то, что для получения замкнутой кривой одного оборота по окружности оказалось недостаточно — их потребовалось уже 3 и 4 соответственно. Это явилось следствием того, что период второго вектора не укладывается нацело в период первого вектора.

Можно и дальше добавлять векторы и получать всё более и более сложные фигуры:

$f(t)=i \left(i^{-t}+1.9 i^{\frac{2 t}{3}}+i^{-2 t}\right)$

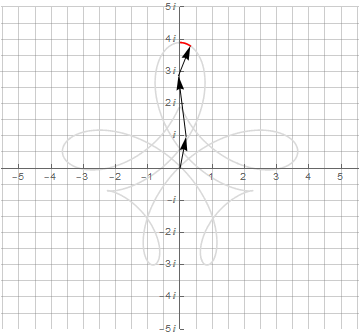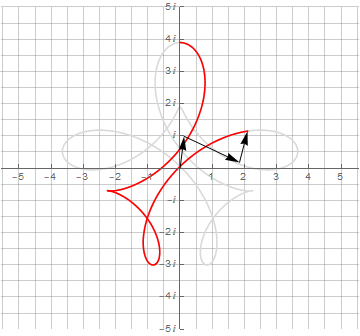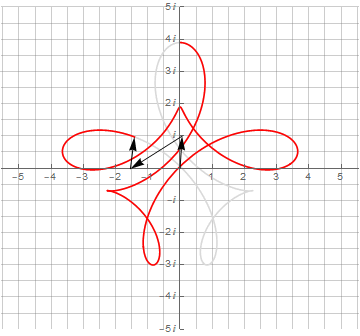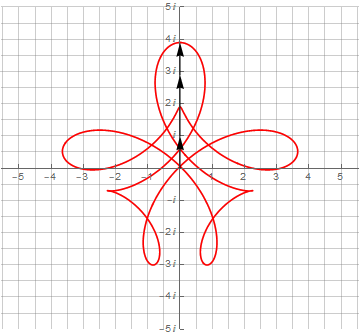
▍ Синусы и синусоидные ленты

Давайте немного отвлечёмся от окружностей и начертим синус. Традиционная запись синусоиды выглядит так:

$y=\sin (x)$

В комплекcном виде формула для синусоды выглядит не намного сложнее

$f(t)=t+i \sin (t)$

а график, естественно, выглядит аналогично:

Легко видеть, как была получена это формула — правую часть равенства мы умножили на мнимую единицу, знак равенства заменили на плюс, а $x$ и $y$ заменили на одну и ту же параметрическую переменную — $t$ . Принципиальная разница между этими формулами получилась в том, что теперь можно взять и повернуть синусоиду, просто умножив её на единичный вектор с нужным углом наклона (здесь 45°). Подобные трансформации синусодиды могут потребоваться для того, чтобы направлять её вдоль заданных кривых:

В параметрической форме записи можно модулировать координаты, получая таким образом различные деформации синусоиды, на первый взгляд не имеющих ничего общего с оригиналом:

$f(t)=t+\frac{3}{8} \sin (2 \pi t)+i \cos (\pi t)$

$f(t)=3 t+i^t-\frac{7}{5} i^{3 t}+3 i^t$

$f(t) = 3 t+i^t+\frac{39}{20} i^{3 t}+3 i^t$

$f(t) = t+2 \sin (t)+\sin (2 t)+i \left(3 \cos \left(\frac{3 t}{2}\right)\right)$

Количество синусоид можно увеличивать, добиваясь эффекта заполнения пространства за счёт равномерного сдвига фаз между ними:

$f(t) = t+i \cos \left(\frac{2 \pi j}{n}+\pi t\right)$

Здесь $n$ — количество синусоид, а $j$ — порядковый номер синусоиды.

Смещение можно задавать и просто смещением координат — как по одной координате, так и по двум:

$f(t) =t+\frac{3}{8} \sin (2 \pi t)+\frac{2 j}{n}+i \cos (\pi t)$

$f(t) =t+\frac{3}{8} \sin (2 \pi t)+\frac{4 j}{n}+i \cos (\pi t)+i j$

▍ Розетты

Теперь можно попробовать и более сложные варианты — добавить фигурам заполнения. Есть два пути для этого:
1) взять центральную кривую, от которой в обе стороны осциллирует синусоида. Это творческий метод, поскольку внутренняя и внешняя огибающие будут зависеть от множества параметров и могут оказаться весьма неожиданными. Здесь также дополнительной сложностью будет вычисление нормали для синусоидной ленты. Несмотря на то, что её легко вычислить дифференцированием нашей кривой (и умножением на мнимую единицу) с последующей нормировкой функцией $sgn(x)$

, более интересные варианты получаются заданием её явным образом, в простейшем случае — нормалью к окружности.
2) явно задать внутреннюю и внешние огибающие, а конкретную точку между ними находить интерполяцией всё той же синусоидой. Этот вариант чуть сложнее, зато более предсказуемый.

Начнём с простого:

$f(t) =i^{-t}+3 i^t+i^t \sin \left(\frac{8 \pi t}{5}\right)$

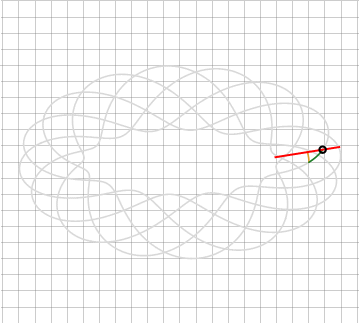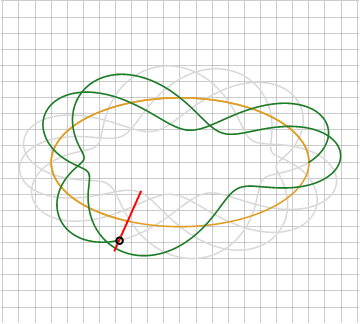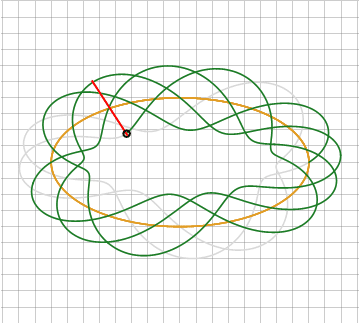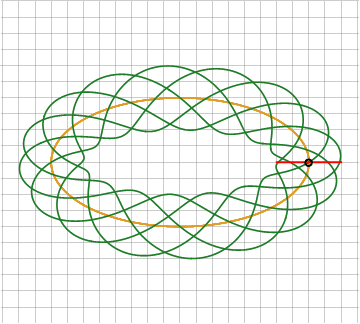
Обратите внимание: здесь мы не использовали синусоидную ленту —, а обошлись лишь одной синусоидой, с некратным периодом 8/5. Для того, чтобы она замкнулась, потребовалось 5 полных оборотов (да, совпадение со знаменателем периода не случайно). Также обратите внимание, что направляющая для синусоиды не перпендикулярна центральной линии — потому что это условие в неё и не закладывалось. А если мы захотим его заложить — то потребуется продифференцировать кривую и повернуть её на 90° умножением на мнимую единицу:

$(i^{-t}+3 i^t)'=\frac{\pi i^{-t}}{2}-\frac{3 \pi i^t}{2}$

Как видно, получился тоже эллипс, только с другим масштабом (и сдвигом фазы на 90° что в нашем случае значения не имеет). Используя эту функцию (с коррекцией масштаба) в качестве направляющей для синусоидной ленты получим следующую формулу:

$f(t) = \frac{1}{4} \left(i^{-t}-3 i^t\right) \sin \left(\frac{2 \pi j}{n}+4 \pi t\right)+i^{-t}+3 i^t$

Последний штрих — нормировать длину направляющей к единице, чтобы ширина заполняющей ленты была одинаковой (или явно заданной амплитуды). Сделать это можно функцией $sgn$ или, что то же самое, через деление на абсолютное значение (которое считается как квадратный корень суммы квадратов мнимой и действительной части).

$f(t) = i^{-t}+3 i^t+\frac{\left(i^{-t}-3 i^t\right)}{\left| i^{-t}-3 i^t\right| }\sin \left(\frac{2 \pi j}{n}+4 \pi t\right)$

Ну и напоследок — несколько примеров «творческих» орнаментов, полученных просто случайным подбором параметров:

$f(t) = \left(2 i^t-i^{-t}\right) \left(\cos \left(5 \pi \left(k+\frac{t}{2}\right)\right)+\frac{1}{2} \cos \left(11 \pi \left(k+\frac{t}{2}\right)\right)\right)+8 i^t+i^{-t}$

$f(t) = \left(3 i^t+i^{-3 t}\right) \left(\cos \left(7 \pi \left(k+\frac{t}{2}\right)\right)+\frac{1}{2} \cos \left(7 \pi \left(k+\frac{t}{2}\right)\right)\right)+8 i^t+i^{-3 t}$

$\small f(t) = (3 \cos (\pi t)+2 i \sin (\pi t)) (3 \cos (11 \pi (k+t))+\cos (7 \pi (k+t)))+9 (4 \cos (\pi t)+2 i \sin (\pi t))$

$f(t) = i^t \left(\cos \left(20 \pi \left(k+\frac{t}{2}\right)\right)+\cos \left(16 \pi \left(k+\frac{t}{2}\right)\right)\right)+4 i^t$

▍ Розетты с интерполяцией

Для второго подхода, интерполяцией между двумя явно заданными огибающими, потребуется вспомогательная функция для изменения масштаба:

$f(x) = \frac{y_{\max } \left(x-x_{\min }\right)+\left(x_{\max }-x\right) y_{\min }}{x_{\max }-x_{\min }}$

в которой при изменении $x$ в диапазоне от $x_{\min}$ до $x_{\max}$ результат функции изменяется соответственно в диапазоне от $y_{\min}$ до $y_{\max}$ . Во многих системах компьютерной алгебры существуют уже предопределённые функции для этого, и в частности в Wolfram Мathematica ею является функция $Rescale\left[x,\left\{x_{\min },x_{\max }\right\},\left\{y_{\min },y_{\max }\right\}\right]$ . Далее мы будем пользоваться таким же синтаксисом — группируя входные и выходные границы в фигурные скобки, для наглядности.

Итак, если в качестве границ взять эллипс и круг, то получится что-то вроде этого:

$f(t) = Rescale\left[\cos \left(\frac{13 \pi t}{5}\right),\{-1,1\},\left\{i^t,i^{-t}+3 i^t\right\}\right]$

Эту формулу можно записать явным образом без использования функции $Rescale$ , подставив аргументы в её определение и упростив:

$f(t) = \frac{1}{2} i^{-t} \left(4 i^{2 t}+\left(1+2 i^{2 t}\right) \cos \left(\frac{13 \pi t}{5}\right)+1\right)$

Однако в таком случае логика работы этой формулы становится намного менее очевидной, и вносить в неё изменения исходя из изначальной логики построения становится намного сложнее.

Поскольку огибающие нам точно известны, то такие фигуры можно комбинировать, использовав одну и ту же огибающую для соседних фигур:

$f_1(t) = Rescale\left[\cos \left(\frac{13 \pi t}{5}\right),\{-1,1\},\left\{i^t,8 i^t \sqrt{\frac{2}{20-12 \cos (\pi t)}}\right\}\right]$

$f_2(t) = Rescale\left[\cos \left(\frac{13 \pi t}{5}\right),\{1,-1\},\left\{3i^t,8 i^t \sqrt{\frac{2}{20-12 \cos (\pi t)}}\right\}\right]$

Или чуть сложнее:

$\small f_1(t) =Rescale\left[\cos \left(\frac{24 \pi t}{5}\right),\{-1,1\},\left\{i^t-\frac{2 i^{5 t}}{35}+\frac{i^{9 t}}{189},2 \left(\frac{3 i^{-5 t}}{70}+\frac{i^{-t}}{4}+i^t+\frac{i^{9 t}}{252}\right)\right\}\right]$

$\small f_2(t) =Rescale\left[\cos \left(\frac{24 \pi t}{5}\right),\{-1,1\},\left\{3 \left(-\frac{1}{12} i^{-3 t}+\frac{i^{-t}}{4}+i^t\right),2 \left(\frac{3 i^{-5 t}}{70}+\frac{i^{-t}}{4}+i^t+\frac{i^{9 t}}{252}\right)\right\}\right]$

Огибающие, вообще говоря, не обязаны быть гладкими. Используя ранее выведенную формулу, в качестве огибающих можно использовать и многоугольники:

$f(t) = Rescale\left[\cos \left(\frac{33 \pi t}{5}\right),\{-1,1\},\left\{2 i^t,\frac{i^t \left(i^{n t}\right)^{1/n}}{1+\left(i^{n t}\right)^{2/n}}\right\}\right],n \to 3$

Огибающие можно сделать более выраженными, если синусоиду немного «оквадратить»:

$f(t) = \sin \left(\frac{1}{2} \pi \sin (t)\right)$

$f(t) = -i \text{Rescale}\left[\sin \left(\frac{1}{2} \pi \sin \left(\frac{31 \pi t}{5}\right)\right),\{-1,1\},\left\{\frac{i^t \left(i^{4 t}\right)^{1/4}}{1+\left(i^{4 t}\right)^{2/4}},\frac{2 \left(i^t \left(i^{5 t}\right)^{1/5}\right)}{1+\left(i^{5 t}\right)^{2/5}}\right\}\right]$

Можно пойти ещё дальше по пути выпрямления и вместо заполнения синусоидой просто использовать прямые отрезки:

$f(t) = i^t \csc \left(\frac{1}{5} \left(\pi -\sin ^{-1}\left(\sin \left(\frac{5 \pi t}{2}\right)\right)\right)\right)$

▍ Бордюры

Вместо того, чтобы строить синусоидные ленты очевидным способом, их тоже можно получать интерполяцией между двумя прямыми:

$f(t) = Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\{t-i,t+i\}\right]$

Если эту формулу символьно вычислить и упростить, то получим уже известную формулу синусоиды в параметрическом виде: $f(t)=t+i \cos \left(\pi \left(\frac{j}{n}+t\right)\right)$

Запись через функцию $Rescale$ позволяет более просто контролировать границы ленты для того, чтобы их можно было собирать как пазл. Например, сделав одну сторону короче другой, можно получить угол в 45° и собрать рамку:

$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\{2 t,t+i\}\right],-1\leq t\leq 1$

В качестве границ интерполяции можно брать и любые другие кривые:

$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\left\{t,t+\frac{1}{2} i \cos (\pi t)+i\right\}\right]$

$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\left\{t-\frac{1}{5} \sin (\pi t),t+\frac{1}{2} i \cos (\pi t+\sin (\pi t))+i\right\}\right]$

$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\left\{t-\frac{1}{2} i \cos \left(\frac{\pi t}{3}\right)-i,t+\frac{1}{2} i \cos (\pi t)+i\right\}\right]$

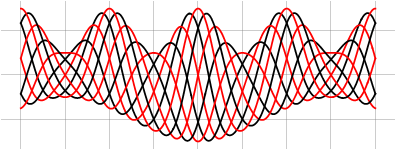
Можно добавить вариативности и заполнению, модулируя либо координаты границ интерполяции

$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\left\{t+\frac{1}{5} \sin (\pi t),t+\frac{1}{2} i \cos (\pi t)+i\right\}\right]$

$f(t) =Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\left\{t-\frac{1}{5} \sin (\pi t),t+\frac{1}{2} i \cos (\pi t)+i\right\}\right]$

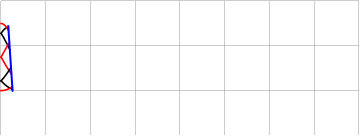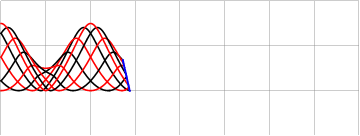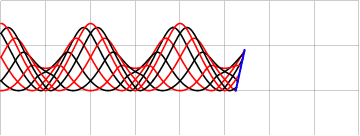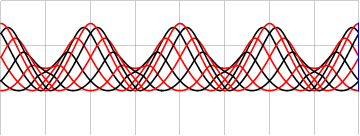
либо частоту заполняющей синусоиды

$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)+\cos (\pi t)\right),\{-1,1\},\{t,t+i\}\right]$

$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)+2 \cos ^3(\pi t)\right),\{-1,1\},\{t,t+i\}\right]$

▍ Заключение

Здесь были рассмотрены самые простые, базовые техники и фигуры. В качестве дальнейшего развития можно использовать и более сложные математические модели для описания огибающих, в том числе кусочно-непрерывные функции типа кривых Безье, и различные варианты их заполнения. Также комплексные числа можно использовать не только для графики как таковой, но и для описания траекторий различных механизмов типа механизма Чебышёва, что позволит аналитически находить оптимальные параметры и свойства таких механизмов. А если с комплексных чисел перейти на кватернионы — то можно рассматривать подобные построения и в 3Д-пространстве.

Разумеется, подобные задачи можно решать и без комплексных чисел — используя векторы и матричное исчисление, как собственно в основном все и делают. Однако комплексные числа представляются более подходящим инструментом для этого — как минимум более компактным, наглядным и с бОльшим простором для манипуляций, включая интегрирование/дифференцирование, разложение в ряд, преобразование Фурье и прочие инструменты функционального анализа. Впрочем, тема «комплексные числа vs. матрицы» выглядит довольно холиварной — поэтому и продолжить её предлагается уже в комментариях.