Коммивояжёр за полином*

Всегда много путей достичь цель есть. Испробовать их все должны вы.
Магистр Йода, из книги «Ученик джедая. Битва за истину», Джуд Уотсон
Задача коммивояжёра, пожалуй самая известная задача комбинаторной оптимизации. Сводится она к поиску самого короткого маршрута проходящего через все заданные пункты. Долгое время задача коммивояжёра считалась трансвычислительной задачей. Нахождение точного решения методом перебора на классическом компьютере размером с Землю уже при n > 66 вершин, требовало бы время большее, чем время существования вселенной.
Однако есть способы, как значительно ускорить нахождение минимального решения за разумное время. Мы будем говорить о точном решении, но всё же стоит помнить о том, что используя в расчётах арифметику с плавающей запятой хоть и двойной точности, мы можем получить накопление ошибки. Данные ошибки вычислений в некоторых ситуациях могут немного повлиять на конечный результат, но мы с вами постараемся избежать таких узких мест.
В данной работе хочу предложить вам быстрые open-source решения, которые вы можете применять в своих проектах.
Ранее мы уже говорили о способах нахождения точного решения методом динамического программирования и методе ветвей и границ, а также методе целочисленного линейного программирования. Последний и стал основой для текущего решения.
И так приступим.

Нет, это не реплика знаменитого квадрата, так выглядит полносвязный граф всего на 200 вершин
Вы можете видеть полносвязный симметричный граф на плоскости. Полносвязный означает, что каждая вершина данного графа связана с другой вершиной ребром. Из всего множества данных рёбер мы должны выбрать только n рёбер, где n — число вершин, которые и будут составлять минимальный Гамильтонов цикл.
Каждое ли из рёбер этого графа может входить в минимальный путь? Если допустить, что некоторые рёбра никак не могут войти в оптимальный путь, то можно значительно уменьшить число комбинаций необходимых для нахождения точного решения. В предыдущей работе мы уже пытались найти такую эвристику, но она не давала сто процентного результата. Теперь же предлагаю рассмотреть новый подход, который гарантированно отсекает невозможные условия, позволяя ускорить поиск решения.
Мы будем производить разбиение исходного множества вершин на симплексы (треугольники для плоскости), то есть осуществим триангуляцию графа. Процедуру разбиения мы будем проводить не случайным образом, а используя триангуляцию Делоне.
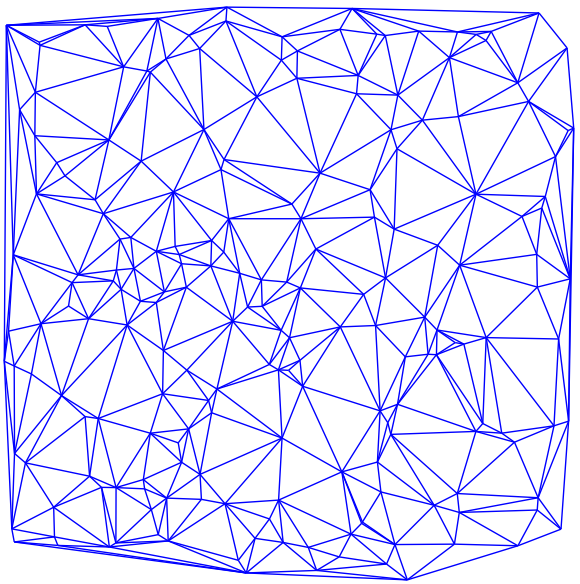
Триангуляция Делоне
Триангуляция Делоне очень мощный метод, который позволяет покрыть исходный граф симплексами, имеющими максимальное значение минимального угла, что в свою очередь позволяет избегать тонких треугольников. Трудоёмкость данной задачи в худшем случае не превышает O (N log N), что играет нам на руку.
Далее мы будем создавать «каркас» графа, используя триангуляцию Делоне, в котором и будем искать минимальное решение. Некоторые исследователи используют полученный граф для быстрого нахождения приближённого решения, но оно редко бывает оптимальным, так как зачастую не включает лучшее решение. Мы же пойдём дальше, добавив к множеству «каркаса» дополнительный набор рёбер. Процедура будет звучать следующим образом:
Для каждой пары смежных рёбер графа, образованного посредством триангуляции Делоне добавляется ещё одно ребро, соединяющее не смежные вершины данных рёбер.

Граф для поиска минимального решения
В результате получается граф, который точно содержит минимальное решение. Данный факт получен эмпирическим путём, а затем многократно подтверждён численным моделированием. Однако чёткого математического доказательства у меня пока нет. Возможно кто-то из читателей сможет доказать данную теорему. Укажем, что одно из рёбер для произвольной вершины всегда будет входить во множество «каркаса», так как оно будет минимальным текущим для вершины, а вот второе необязательно.
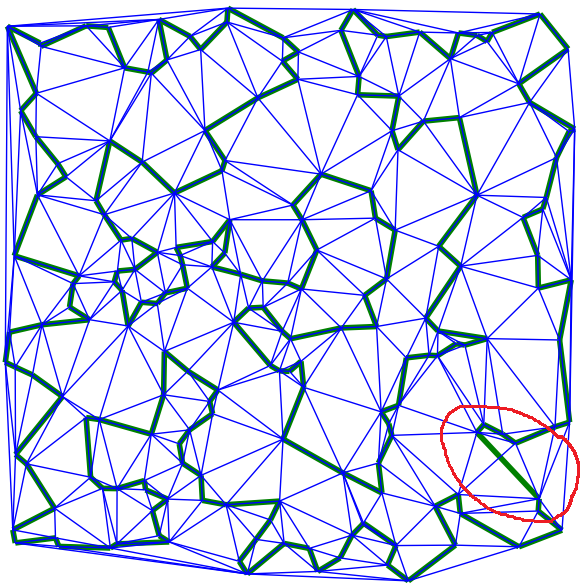
Минимальный Гамильтонов цикл
Обратите внимание, как раз тот случай, когда для построения точного минимального пути рёбер графа образованных только триангуляции Делоне недостаточно.
Что нам даёт подход описанный выше?
В полносвязанном симметричном графе содержится (n^2 — n) / 2 рёбер, а в итоговом графе по схеме выше только ~ O (c * n), где с < 10 константа – приближённая верхняя оценка для Евклидовой плоскости, реально несколько меньше 10.
Пример: для n ≤ 20: эффекта нет, но уже при n = 200: нужно приблизительно в десять раз меньше рёбер, а при n = 2000: нужно, примерно, в сто раз меньше рёбер, как если бы мы использовали полносвязный граф. Любое отброшенное ребро значительно уменьшает количество вычислений для любого алгоритма поиска оптимального пути.
В итоговом графе мы можем искать минимальное решение любым известным нам методом. Например, перебором грубой силой, ветвями и границами, муравьиным и др. Однако самый лучший эффект дают методы, использующие линейное программирование.
Читателям незнакомых с линейным программированием скажу, что это невероятно мощный инструмент для нахождения решения систем линейных уравнений. Я бы даже поставил его на середину пути между классическими комбинаторными и квантовыми вычислениями. К сожалению, из-за ограничений метода только малый класс сложных задач можно решать с помощью линейного программирования. Концептуально суть линейного программирования сводится к построению вычислительного поля, в рамках которого ищется решение с минимальной (максимальной) суммой энергии связей, удовлетворяющих граничным условиям.
Метафорически решение системы линейных уравнений можно представить следующим образом. Представьте себе футбольный мяч, швы которого это связи между решеними, а углы швов — это сами решения.

В решении целочисленных задач используются вариации симплекс-метода. Алгоритм начинает решение из некой вершины и «шагает» по швам в том направлении, которое соответствует минимальному решению и игнорирует другие не оптимальные направления. Решение находится за конечное число шагов.
Однако метафора с мячом не совсем верная, так как мяч имеет единичный радиус для любой вершины. Нужно упомянуть о том, что есть ещё целевая функция, которая дополнительно задаёт неровности в вершинах мяча, что-то вроде гор и каньонов. Поиск оптимального решения ведётся уже с учётом данной топологии. Иногда выгоднее обойти гору, чем подниматься на неё.
В нецелочисленном линейном программировании часто алгоритм не желает двигаться именно по «швам мяча», часто он сокращает путь по «целине», хотя и строго линейно. Целочисленное же программирование, за счёт дополнительных усилий (вычислительно не дешёвых) не позволяет отклоняться от прямых маршрутов.
Метафора с мячом будет вполне адекватна, если только уточнить, что такой гипермяч находится в многомерном пространстве и выбора направлений на каждом шаге может быть больше, чем два.
Знающий читатель может возразить, что в метафоре должен быть многомерный гиперкуб, мы же будем исходить из того, что мяч проще представить.
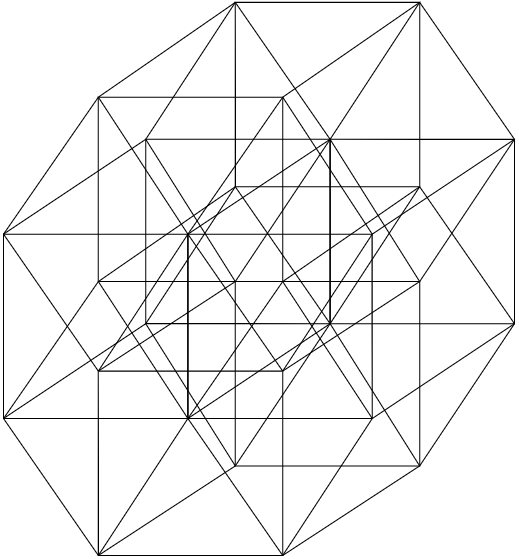
Пятимерный гиперкуб (Пентеракт).
Даже страшно представить, как должен выглядеть тысячемерный гиперкуб, а именно с такими структурами и работает линейное программирование. Каждая новая переменная (ребро) в задаче добавляет ещё одну мерность к гиперкубу, в котором производится поиск решения.
Раз уж мы высказались за open-source решения, то было бы уместно использовать только те инструменты при реализации, которые с одной стороны были бы в открытом доступе, а с другой имели достаточно высокую производительность.
Ваш покорный слуга сделал ставку на распространённые инструменты, которые показались ему наиболее удобными для реализации текущей задачи:
1. NetworkX — библиотека, для работы с графами и иными сетевыми структурами. Является свободным программным обеспечением, распространяемым по лицензии BSD.
2. SciPy — библиотека с открытым исходным кодом, предназначенная для выполнения научных и инженерных расчётов.
3. Matplotlib — библиотека для визуализации данных двумерной и трёхмерной графикой, распространяется на условиях BSD-подобной лицензии. Она не нужна для расчётов, а используется только для визуализации графов.
4. Pulp — Открытая библиотека предназначенная для решения задач линейного программирования.
Для решения задач целочисленного (смешанного) линейного программирования, автором применялись следующие решатели:
Все указанные солверы подходят для нахождения решения задачи коммивояжёра. Однако решатели CBC и ORTOOLS, хоть и не являются самыми быстрыми в предложенном списке, имеют бóльшую точность при нахождении решения. А так как автор утверждает, что может получить именно точное решение, то это критично. Хотя решатель ORTOOLS от Google и задействует все ядра процессора, на конкретно этой задаче в разы проигрывает однопоточному консольному решателю CBC от COIN-OR. CBC входит в поставку по умолчанию Pulp, где является основным решателем.
Несколько замечаний по поводу текущего алгоритма:
В текущей реализации мне показалось более удачным задавать только список вершин, длину ребра алгоритм рассчитывает самостоятельно (через Евклидову норму). На больших размерностях графа, матрица смежности становится просто монструозной. В данном случае мы используем networkx.Graph (), который сохраняет только нужные рёбра в виде списков смежности.
Не допускается задавание задание вершин в виде одной линии, так как для триангуляции Делоне требуется минимум двумерное пространство.
Не допускаются две вершины с одинаковыми координатами, так как это не имеет смысла и мешает расчётам. Такие вершины нужно считать, как одну.
Алгоритм способен решать задачу, в трёхмерном или выше пространствах. Для этого требуется внести небольшие правки. Однако от увеличения метрики пространства сильно ухудшается качество отсева рёбер, а следовательно и прирост производительности.
Сам метод решения симметричной задачи коммивояжёра мы уже рассматривали в прошлых статьях и здесь только очень кратко повторим основные тезисы:
Каждое ребро задающего графа это целочисленная переменная решателя линейных уравнений. Сколько рёбер в графе, столько и переменных. Каждая из таких переменных может принимать только два значения 1 или 0. (Выбираем данное ребро в граф результат или нет). В результате решения количество единиц должно быть равно числу вершин графа.
Каждое ребро имеет свою длину и эта длина указывается в целевой функции при соответствующей переменной.
Для каждой вершины существует строго два пути: по одному мы приходим в вершину, через другой покидаем её. Мы отражаем это условие в виде линейного условия, что сумма всех рёбер для каждой из вершин равно двум.
После решаем систему линейных уравнений. Если в результате решения граф разваливается на несколько подциклов, то вносим дополнительные условия нераспадаемости и снова решаем полученную систему уравнений.
Условие нераспадаемости можно задать двумя эквивалентными способами. Первый заключается в том, что сумма переменных подцикла не должна превышать количества вершин его составляющих минус один. Второй говорит о том, что сумма внешних связей для каждого из подцикла больше или равна двум. Мы выбираем то из условий, что задействует меньшее число переменных, чтобы помочь решателю найти решение быстрее.
Простой пример решения, модель PuLP
[[ 0 8 34 40 50 71]
[ 8 0 42 44 50 74]
[34 42 0 26 54 58]
[40 44 26 0 30 34]
[50 50 54 30 0 32]
[71 74 58 34 32 0]]tsp:
MINIMIZE
8*x00 + 34*x01 + 40*x02 + 50*x03 + 71*x04 + 42*x05 + 44*x06 + 50*x07 +
74*x08 + 26*x09 + 54*x10 + 58*x11 + 30*x12 + 34*x13 + 32*x14 + 0
SUBJECT TO
_C1: x00 + x01 + x02 + x03 + x04 = 2
_C2: x00 + x05 + x06 + x07 + x08 = 2
_C3: x01 + x05 + x09 + x10 + x11 = 2
_C4: x02 + x06 + x09 + x12 + x13 = 2
_C5: x03 + x07 + x10 + x12 + x14 = 2
_C6: x04 + x08 + x11 + x13 + x14 = 2
VARIABLES
0 <= x00 <= 1 Integer
0 <= x01 <= 1 Integer
0 <= x02 <= 1 Integer
0 <= x03 <= 1 Integer
0 <= x04 <= 1 Integer
0 <= x05 <= 1 Integer
0 <= x06 <= 1 Integer
0 <= x07 <= 1 Integer
0 <= x08 <= 1 Integer
0 <= x09 <= 1 Integer
0 <= x10 <= 1 Integer
0 <= x11 <= 1 Integer
0 <= x12 <= 1 Integer
0 <= x13 <= 1 Integer
0 <= x14 <= 1 Integerx00 (1, 0) = 1.0 weight = 8
x01 (2, 0) = 1.0 weight = 34
x05 (2, 1) = 1.0 weight = 42
x12 (4, 3) = 1.0 weight = 30
x13 (5, 3) = 1.0 weight = 34
x14 (5, 4) = 1.0 weight = 32
Result = 180
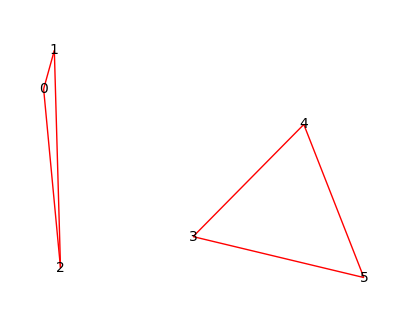
Шаг 1
tsp:
MINIMIZE
8*x00 + 34*x01 + 40*x02 + 50*x03 + 71*x04 + 42*x05 + 44*x06 + 50*x07 +
74*x08 + 26*x09 + 54*x10 + 58*x11 + 30*x12 + 34*x13 + 32*x14 + 0
SUBJECT TO
_C1: x00 + x01 + x02 + x03 + x04 = 2
_C2: x00 + x05 + x06 + x07 + x08 = 2
_C3: x01 + x05 + x09 + x10 + x11 = 2
_C4: x02 + x06 + x09 + x12 + x13 = 2
_C5: x03 + x07 + x10 + x12 + x14 = 2
_C6: x04 + x08 + x11 + x13 + x14 = 2
_C7: x00 + x01 + x05 <= 2
_C8: x12 + x13 + x14 <= 2
VARIABLES
0 <= x00 <= 1 Integer
0 <= x01 <= 1 Integer
0 <= x02 <= 1 Integer
0 <= x03 <= 1 Integer
0 <= x04 <= 1 Integer
0 <= x05 <= 1 Integer
0 <= x06 <= 1 Integer
0 <= x07 <= 1 Integer
0 <= x08 <= 1 Integer
0 <= x09 <= 1 Integer
0 <= x10 <= 1 Integer
0 <= x11 <= 1 Integer
0 <= x12 <= 1 Integer
0 <= x13 <= 1 Integer
0 <= x14 <= 1 Integerx00 (1, 0) = 1.0 weight = 8
x01 (2, 0) = 1.0 weight = 34
x07 (4, 1) = 1.0 weight = 50
x09 (3, 2) = 1.0 weight = 26
x13 (5, 3) = 1.0 weight = 34
x14 (5, 4) = 1.0 weight = 32
Result = 184

Шаг 2
Евклидова задача коммивояжёра подходит для расчёта маршрута полёта квадрокоптеров. Использование кратчайшего маршрута вполне применимо в движении в автоматическом режиме. Например, посещение определённых точек местности при аэрофотосъёмке с малой высоты, доставка большого числа небольших объектов множеству адресатов (почта).
Так же эффект даст нахождение кратчайшего пути в промышленном производстве. На рабочей поверхности (печатной плате) нужно нанести множество точечных технологических операций, например, сверление отверстий, установка заклёпки, установка скобы пневмостеплером, нанесение монтажного клея, точечная сварка и др. Использование кратчайшего пути позволит ускорить технологический процесс, за счёт уменьшения времени перемещения инструмента между точками технологических операций.
Как привило, такие операции наносятся последовательно вдоль одной из осей, с последовательным переходом от одной точки контакта к другой, как в струйном принтере.
Проиллюстрируем:
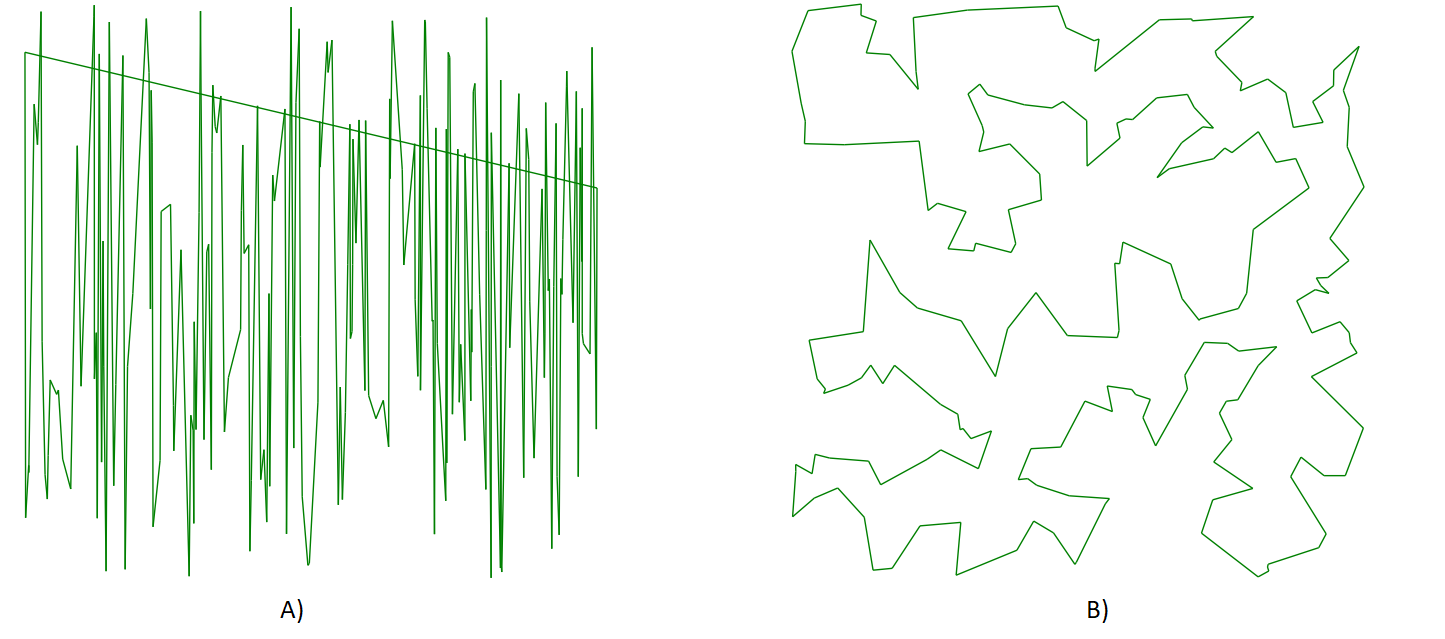
Обход графа на 200 вершин: A) вдоль оси x; B) минимальный Гамильтонов цикл;
На приведённом выше изображении путь, полученный благодаря решению задачи коммивояжёра, примерно в 6 раз короче. Чем больше вершин в графе, тем выше данное соотношение.
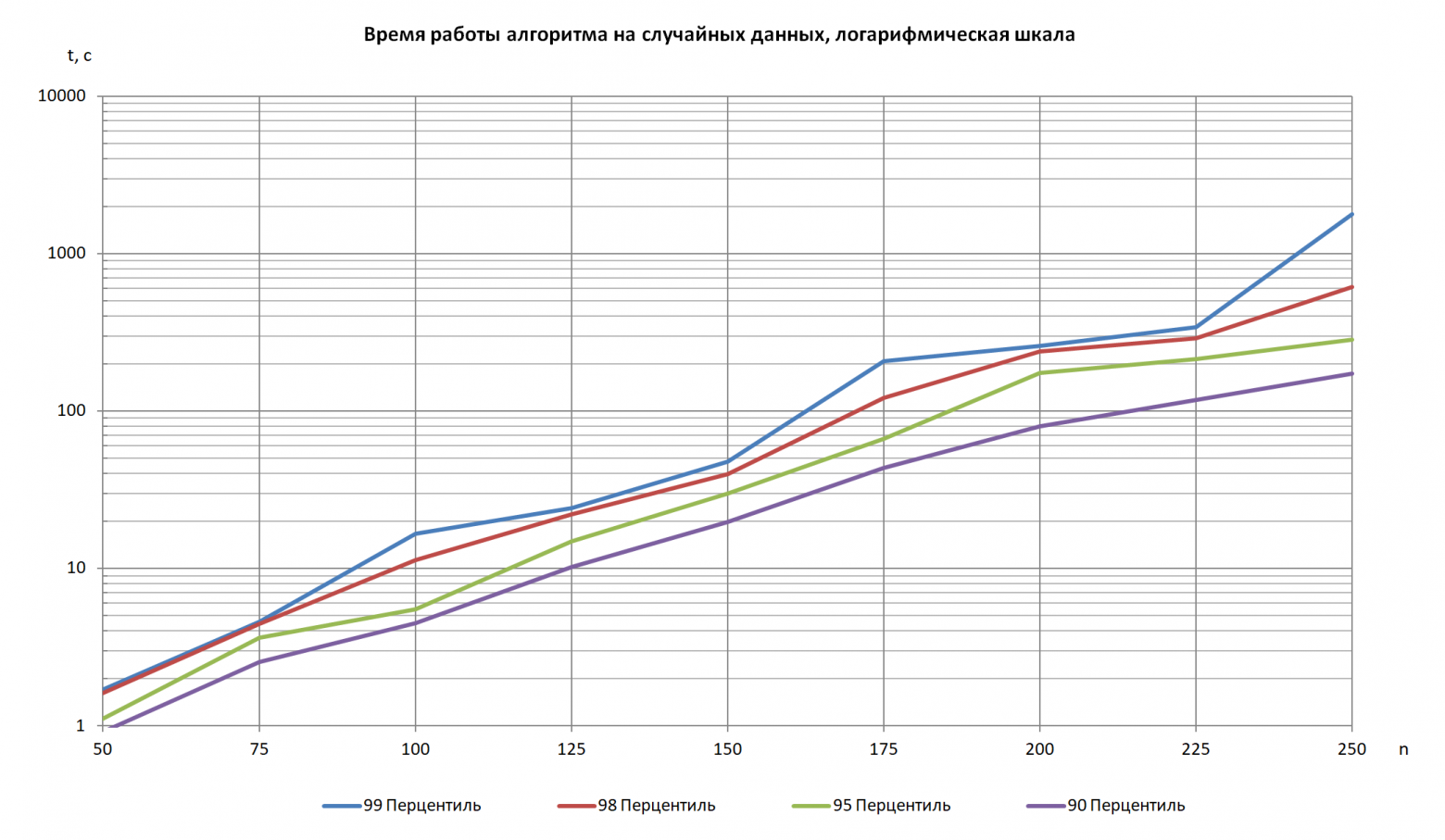
Зависимость времени работы алгоритма от размера входных данных
Существует важное применение задачи коммивояжёра, где не подходит описанный симметричный алгоритм — это расчёт дорожных расстояний. Так как дорожная сеть, как правило, состоит из криволинейных участков местности, а также односторонних участков пути, мы не можем использовать Эвклидову задачу коммивояжёра. В таком случае нужно использовать ассиметричную задачу коммивояжёра.
Ассиметричная задача примеяется так же для поиска кратчайшей общей суперпоследовательности, которая в сою очередь используется при секвени́ровании ДНК, а так же в сжатии данных.
Асимметричная задача коммивояжёра
Мы будем использовать описание задачи в формулировке Данцига, Фултона, Джонсона.

Решать будем так же с помощью целочисленного линейного программирования.
От себя добавим только одно изменение: мы не будем закладывать все условия, гарантирующие исключение подтуров. Если мы укажем в условии решения сразу все ограничения, а их число близко к 2^n, то задача становится практически не решаемой при сколько-нибудь значимых n.
Вместо этого предлагаю разбить задачу на ряд более простых подзадач, последовательное решение которых приведёт нас к результату гораздо быстрее. То есть мы будем добавлять только те ограничения, которые будут необходимы на текущем этапе для конкретной задачи. После чего будем перезапускать решатель с вновь добавленными ограничениями до получения финального результата. Собственно, этот же подход мы уже применяли для нахождения решения симметричной задачи.
Основная мысль подхода: Несколько мелких задач решаются намного быстрее одной большой!
Линейные условия задаются практически точно так же как в симметричной задаче. Однако нужно понимать, что в ассиметричной задаче прямой и обратный пути не обязательно равны. Более того, прямой или (и) обратный путь может отсутствовать.
Потому для каждой вершины мы задаём сразу два условия:
Сумма исходящих рёбер для каждой вершины должна быть равна единице.
Сумма входящих рёбер для каждой вершины должна быть равна единице.
А в условии нераспадаемости, альтернативы звучат так:
Сумма переменных каждого найденного подцикла не должна превышать количества вершин, его составляющих минус один.
Сумма внешних исходящих связей для каждого найденного подцикла не меньше единицы.
Сумма внешних входящих связей для каждого найденного подцикла не меньше единицы.
Мы так же выбираем условие с наименьшим числом задействованных переменных.
В отличие от Эвклидовой задачи коммивояжёра, достаточно сложно подобрать адекватные тестовые данные для визуализации процесса решения ассиметричной задачи. Но так как данная задача является более общей для симметричного алгоритма, то можно использовать те же наборы исходных данных. Результаты получаются аналогичные, но гораздо медленнее. Думается, что удаление части рёбер и загрубление рёбер до целого значения является вполне удачным примером демонстрации работы алгоритма.
Пошаговый пример решения:
В сети довольно сложно найти датасеты для проверки предложенного ассиметричного алгоритма. Примеры, что мне удавалось найти в основном на соединение точек на карте, но там симметричные наборы. Наиболее подходящий набор получен на ветхой страничке Гейдельбергского университета. Самый большой граф из их набора на 443 вершины обработался за 9 минут на домашнем компьютере в одном потоке.
Буду рад, если сообщество в комментариях поможет с поиском иных источников релевантных данных.
Любопытным следствием подхода к нахождению решения задачи коммивояжёра, через линейное программирование, является тот факт, что нам не всегда нужно досчитывать программу до финала, если нам нужно только ответить на вопрос:
Возможно ли получить решение длиной меньше L?
На каждом шаге алгоритм возвращает величину, меньше которого невозможно построить минимальный Гамильтонов цикл. С каждым шагом постепенно увеличивая это значение. То есть, если на каком-то шаге алгоритм вернёт минимальную нижнюю оценку больше L, то это означает, что невозможно получить решение короче этой оценки.
Это следствие говорит о том, что получить ответ на данный вопрос иногда проще, чем найти точное решение задачи коммивояжёра.
Благодарю за внимание!
Мне бы хотелось, чтобы подходы и алгоритмы, описанные в данной работе, не исчезли за горизонтом событий орбит крупных корпораций. Поэтому я публикую данную работу под открытой лицензией, и вы можете использовать код по своему усмотрению.
Ссылка GitHub
* Заголовок статьи содержит заявку на то, что задачу коммивояжера, возможно решать за полиномиальное время от числа вершин. Целочисленное линейное программирование является NP-трудной задачей. В среднем разрешается за полиномиальное время, но у неё есть и плохие случаи, когда решение вырождается в O (2^n). Однако в практических задачах такое не происходит, кроме как в специально подобранных условиях. Сложности с решением возникают только в задачах с регулярными повторяющимися элементами одинаковыми по величине. На случайных или слегка рандомизированных выборках время решения стремится к полиному по времени от размера входных данных.
P.S. Таков путь!
