Коды Рида-Соломона. Часть 2 — арифметика полей Галуа02.11.2017 08:18

Здравствуйте, друзья! В прошлый раз мы с вами начали говорить о том, как коды Рида-Соломона помогают обеспечивать необходимый уровень надежности хранения данных. Сегодня остановимся немного подробнее на арифметике полей Галуа, которая используется в расчётах.

Сначала краткий экскурс в прошлую часть. Мы выяснили — чтобы иметь возможность восстанавливать потерянные данные, необходимо сначала определенным образом сгенерировать «избыточные данные». Причем, с математической точки зрения, эта задача (кодирования) сводится к построению некоторой порождающей матрицы и выполнению операции умножения этой матрицы на вектор исходных данных. Процедура восстановления (декодирования), в свою очередь, заключается в обращении порождающей матрицы и умножения её на вектор сохранившихся данных. Схематически это можно изобразить следующим образом.

Процедура кодирования:

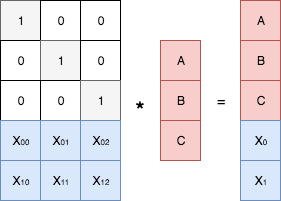
Процедура декодирования:

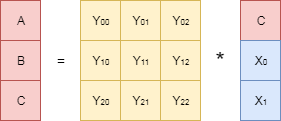
Ограничения арифметики рациональных чисел

Мы уже отмечали некоторые трудности, с которыми приходится сталкиваться при реализации процедур кодирования/декодирования на конкретных аппаратных платформах. Так, например, числа в памяти ЭВМ обычно представлены фиксированным количеством байтов. Как следствие, при умножении элементов порождающей матрицы, можно получить переполнение разрядов. Или при обращении порождающей матрицы в качестве ее элементов могут возникнуть рациональные числа, которые проблематично хранить с произвольной точностью. Поэтому, сегодня мы с вами поговорим о том, как можно реализовать данные процедуры, избегая вышеуказанных проблем. В этом нам поможет теория полей Галуа, о которой мы уже немного говорили в прошлой статье.

Сразу сделаю несколько замечаний. Во-первых, статья прежде всего рассчитана на инженерную аудиторию, поэтому я старался избегать строгих математических определений. Тем, кому хочется более формального введения в данную область, имеет смысл сразу обратиться к соответствующей литературе. Со своей стороны, могу порекомендовать книгу Эрнеста Борисовича Винберга «Курс алгебры». Во-вторых, непосредственно для реализации алгоритмов избыточного кодирования достаточно лишь базового понимания теории конечных полей. Можно просто считать, что заданы некоторые непротиворечивые таблицы умножения, деления, сложения, вычитания и все вычисления происходят с использованием этих таблиц. Это намек для тех, кому не очень хочется глубоко погружаться в данный раздел алгебры.

Поля и арифметические операции в конечных множествах

Прежде чем перейти непосредственно к обсуждению полей Галуа, давайте повторим еще раз, чего мы хотим достичь. Мы хотим иметь возможность умножать матрицы на вектора, обращать матрицы. А самое главное, мы хотим иметь дело только с целыми числами и не переживать за переполнение при выполнении операций умножения и сложения.

Также, во избежание путаницы, имеет смысл сразу разобраться с терминологией. Прежде всего, что такое поле с точки зрения общей алгебры? Как сообщает нам Википедия,»поле — множество, для элементов которого определены операции сложения, вычитания, умножения и деления (кроме деления на нуль), причём свойства этих операций близки к свойствам обычных числовых операций». Что такое поле Галуа? Поле Галуа — это произвольное поле, состоящие из конечного числа элементов. $GF(p)$ , $GF(p^n)$ — стандартное обозначение полей Галуа, где в скобках указывается количество элементов поля.

В современных ЭВМ для хранения чисел обычно используется фиксированное число бит. Нетрудно посчитать, что всего существует $2^n$ различных n-битовых чисел, от 0 и до $(2^n – 1)$ . Другими словами, мы имеем некоторое конечное множество чисел. На этом множестве мы сейчас попытаемся непротиворечивым образом определить операции умножения, деления, сложения и вычитания. Причем так, чтобы результат любой операции также был $n$ -битовым числом! В этом случае говорят, что множество замкнуто относительно введенных операций.

Операция вычитания в системах конечных множеств обычно вводится через понятие нулевого и противоположного элементов. Нулевой элемент $0$ — это такой элемент, для которого справедливо равенство: $a + 0 = a$ , где $a$ — произвольный элемент множества. Элемент $b$ является противоположным для $a$ , если верно равенство $a + b = 0$ . Обычно противоположный элемент обозначается как $-a$ . Если мы хотим из $x$ вычесть $y$ , мы находим противоположный элемент $-y$ и складываем его с $x$ . Соответственно, для того, чтобы иметь возможность вычитать произвольные элементы конечного множества, каждый элемент этого множества должен обладать противоположным.

Аналогичным образом обстоят дела и с операцией деления. Вводится понятие единичного и обратного элементов. Единичный элемент $1$ — это такой элемент, для которого верно равенство $a * 1 = a$ , где $a$ — произвольный элемент множества. Элемент $b$ (обозначается как $1/a$ ) называется обратным к $a$ , если $a * b = 1$ . Как и при вычитании, если мы хотим $x$ разделить на ненулевой $y$ , мы должны найти обратный элемент $1/y$ и умножить его на $x$ . Для того, чтобы иметь возможность делить произвольные элементы, каждый элемент множества (за исключением нулевого) должен обладать обратным.

Построение полей Галуа GF (p)

Каким образом мы можем определить на конечном множестве чисел указанные арифметические операции, причём так, чтобы множество было замкнуто относительно них? Другими словами, мы хотим произвольное конечное множество элементов превратить в поле Галуа. Первое что приходит в голову, это воспользоваться модульной арифметикой. Тогда если наше множество содержит $p$ элементов, то результатом произведения чисел $a * b$ будет является число $(a * b) mod p$ . Сумма чисел определяется как $(a + b) mod p$ .

В качестве упражнения, давайте составим таблицы сложения и умножения для множества, состоящего из $p = 5$ элементов $\{0, 1, 2, 3, 4\}$ .

На нижних двух таблицах представлены противоположные и обратные значения для каждого элемента нашего множества. Вооружившись этими таблицами, мы можем выполнять все необходимые нам арифметические операции. Ура!

Построение полей Галуа

Кажется, что мы на верном пути к успеху. Единственное, что нас может пока не устраивать, так это размер нашего поля — 5. Понятно, что для упрощения программной реализации, имеет смысл работать с множествами, содержащими $2^n$ чисел. Тогда мы сможем оперировать полубайтами, байтами, словами и т.д.

На первый взгляд кажется, какая разница, — 5 или 256 элементов в множестве, берём результат операции умножения или сложения по соответствующему модулю и готово. Давайте снова попробуем составить таблицу умножения для множества, но на этот раз содержащего $4 = 2^2$ элемента — $\{0, 1, 2, 3\}$ . Вот что получилось:
Таблица умножения для {0,1,2,3}

Если пристально посмотреть на полученную таблицу, можно обнаружить в ней один серьезный недостаток. Обратите внимание на строчку для элемента 2. В этой строчке нет единичного элемента! Это означает, что мы не сможем делить другие элементы на 2, поскольку для него не существует обратного! Значит, необходимо производить построение таблиц сложения и умножения каким-либо другим способом. Модульная арифметика, к сожалению, больше не работает.

Итак, мы выяснили, что если множество содержит $4 = 2^2$ объекта, то модульная арифметика не позволяет задавать непротиворечивые операции умножения. На самом деле, подобные проблемы возникнут для любого множества, количество элементов $p$ которого не является простым числом. Но что ещё можно придумать?

Сложение в GF (p^n)

Давайте пока для простоты считать, что множество, на котором мы хотим определить арифметические операции содержит $2^n$ элементов. Это, собственно говоря, числа $\{0, 1, 2, 3, …, 2^n - 1\}$ . Любое число $a$ из этого множества можно представить в виде разложения:

$a=a_0+a_12^1+a_22^2+...+a_{n-1}2^{n-1}, a_i\in\{0,1\}$

По сути дела, это обычное двоичное представление числа. Таким образом, любое число из нашего множества мы можем также рассматривать как вектор длины $n$ , элементы которого нули и единицы:

$a=[a_0,a_1,a_2,...,a_{n-1}], a_i\in\{0,1\}$

Введём операцию сложения двух любых чисел через сложение соответствующих векторов двоичного разложения. Причем сложение компонентов векторов мы будем вести по модулю 2 (в общем случае, если количество элементов $p^n$ , по модулю $p$ ). Таким образом, результирующий вектор также будет двоичным представлением некоторого числа и, как следствие, будет принадлежать нашему множеству (множество будет замкнуто относительно операции сложения).

$a=[a_0,a_1,a_2,...,a_{n-1}], a_i\in\{0,1\}\\ b=[b_0,b_1,b_2,...,b_{n-1}], b_i\in\{0,1\}\\ c=a+b=[(a_0+b_0)mod2,...,(a_{n-1}+b_{n-1})mod2]$

Несложно заметить, что введенная нами операция сложения эквивалентна битовой операции «исключающее ИЛИ» (XOR). Что очень хорошо, поскольку современные процессоры могут выполнять данную операцию чрезвычайно быстро. Но это еще не все. Очевидно, что $a \oplus a = 0$ для произвольного числа $a$ . Это означает, что противоположным элементом к $a$ является сам $a$ . Таким образом, в поле $GF(2^n)$ сложение совпадает с вычитанием!

Умножение в GF (p^n)

Осталось ввести на нашем множестве операцию умножения. Делается это следующим образом. Давайте на время представим, что любое число $a$ из нашего множества — это многочлен следующего вида:

$a(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1},a_i\in{0,1}$

Здесь коэффициенты многочлена берутся из двоичного разложения числа $a$ . При таком подходе, например, числу $100 = 01100100b$ будет поставлен в соответствие многочлен $x^6 + x^5 + x^2$ .

Операцию умножения двух чисел мы можем определить через умножение многочленов, соответствующих данным числам:

$a×b=(a_0+a_1x+...+a_{n-1}x^{n-1})×(b_0+b_1x+...+b_{n-1}x^{n-1})$

Причем при перемножении все операции с коэффициентами многочленов выполняются по модулю 2.

Но теперь, очевидно, может возникнуть другая проблема. При перемножении двух многочленов степени $n-1$ , может получиться многочлен более высокой степени, который не будет соответствовать ни одному из чисел нашего множества. Это решается следующим образом. Выбирается неприводимый многочлен степени $n$ . Грубо говоря, это такой многочлен, который нельзя представить в виде произведения других многочленов, подробнее в статье. После это, используя алгоритм деления многочленов столбиком, который многие могут помнить еще по школьной программе, мы делим результат произведения на неприводимый многочлен. Еще раз напоминаю, что при делении столбиком, операции с коэффициентами многочленов также выполняются по модулю 2. В итоге, получаем многочлен степени, не выше чем $n-1$ , который мы и принимаем за результат произведения двух чисел. Вот пример выполнения умножения двух чисел над полем $GF (2^8)$ с использованием неприводимого многочлена $x^8 + x^4 + x^3 + x + 1$ . Данный многочлен используется в алгоритме шифрования AES/Rijndael.

Мы рассмотрели поле $GF(2^n)$ . Произвольные поля $GF(p^n)$ строятся аналогичным образом, только вместо двоичного представления числа используется $p$ -ичное и все вычисления проводятся по модулю $p$ .

Изоморфизм полей и поля Галуа произвольного размера

А что будет, если выбрать другой неприводимый многочлен? Можно даже поставить более общий вопрос. Предположим, мне вообще не нравятся все эти многочлены и деления столбиком, поэтому я лучше придумаю свою непротиворечивую таблицу умножения используя какой-нибудь другой принцип. Будет ли это чем то, принципиально новым? Ответ — нет. Все эти полученные поля будут изоморфны.

Переводя с «математического» языка, изоморфизм означает, что отличия только в обозначении элементов полей и одно можно свести к другому, выбрав соответствующее правило отображения.

Конечные множества элементов, которые мы рассматривали до сих пор, были двух типов. Первый тип множеств имел число элементов, равное некоторому простому числу $p$ . На таких множествах нам удалось задать таблицы умножения и сложения, используя лишь модульную арифметику. Ко второму типу относятся множества, имеющие $p^n$ , $p$ — простое, , где $p$ простое число, а $n$ любое натуральное.

Все поля размера $p^n$

изоморфны.

Заключение

Вторая статья цикла подходит к концу. В первых двух статьях были представлены краткие теоретические сведения, связанные с кодами Рида-Соломона и полями Галуа. В следующей части планирую более подробно остановиться на особенностях программной реализации упомянутых выше алгоритмов. Спасибо.