Ко-кластеризация: cегментирование данных вдоль и поперёк
Обычно кластеризация подразумевает выделение нескольких групп объектов со схожими характеристиками внутри группы, а между группами — различными. Особенность ко-кластеризации — группирование не только объектов, но и самих характеристик этих объектов. То есть, если данные представлены в виде матрицы, то кластеризация — это перегруппировка строк или столбцов матрицы, а ко-кластеризация — перегруппировка и строк и столбцов матрицы данных.
Как и в предыдущих моих публикациях, примеры использования методов и визуализация решений показаны на данных результатов опросов. Типичная область применения алгоритмов ко-кластеризации — биоинформатика, сегментирование изображений, анализ текстов.

Для ко-кластеризации данных, как и в случае кластеризации, существует много алгоритмов. Википедия сообщает по крайней мере о 22 методах ко-кластеризации. В этой статье будут продемонстрированы возможности только одного из них. Этот метод называют блочной кластеризацией. Его суть лучше всего выразить картинкой, взятой из статьи авторов этого подхода [1].
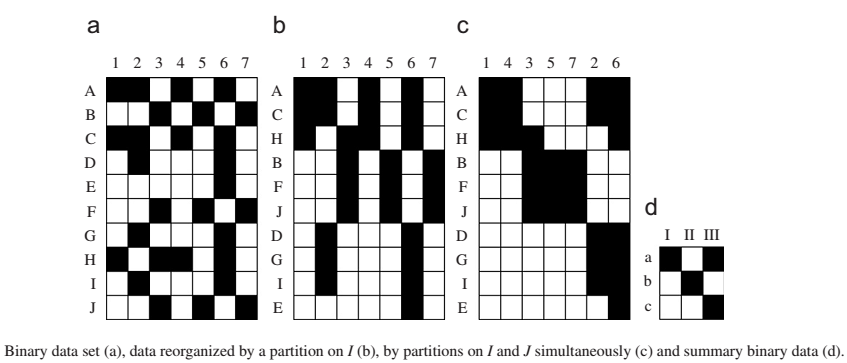
Иными словами задача состоит в том, чтобы из мозаики данных собрать картинку блочного вида. Математически этот метод можно формализовать с помощью процедуры три-факторизации неотрицательных матриц. Пусть V матрица входных данных размера n x m. Требуется представить ее в виде
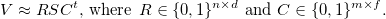
Каждая строка матриц R и C содержит ровно одну единицу, остальные элементы — нули. Единичный элемент (i j) матрицы R указывает, что строка i матрицы V принадлежит j-ому горизонтальному кластеру. Единичный элемент (k l) матрицы С указывает, что столбец k матрицы V принадлежит l-ому вертикальному кластеру.
Матрицы R и C выбираются таким образом, чтобы минимизировать функцию потерь:  В этом случае D определяется через норму Фробениуса
В этом случае D определяется через норму Фробениуса

Эта формализация восходит к работе [2], в которой была предложена ортогональная три-факторизация неотрицательных матриц. Такая постановка задачи позволяет применять итерационные методы нахождения указанного разложения входной матрицы, похожие на методы факторизации неотрицательных матриц.
Но в этой публикации будут рассмотрены примеры блочной кластеризации полученные с помощью метода максимального правдоподобия. Детали алгоритма можно найти в работе [1]. Такой подход, как правило, требует больших вычислительных затрат для нахождения решения. Но есть и преимущества. Во-первых, с помощью такого метода можно автоматически определять оптимальное, с точки зрения алгоритма, число горизонтальных и вертикальных кластеров для категориальных данных [3]. Во-вторых, алгоритм позволяет учитывать тип входных данных — категориальные (в частности, бинарные) или непрерывные (в этом случае не требуется ограничения на то, что входные данные неотрицательны). Для расчетов будет использован пакет blockcluster [4] среды R.

Основной целью этой публикации является демонстрация возможностей визуализации решения кластеризации. Отличительная черта блочной кластеризации, помимо сегментирования данных в обоих направлениях, — при этом виде кластеризации значения входных данных не преобразуются. Производится лишь перестановка строк и столбцов входной матрицы. Это дает возможность наглядно представить as is результат кластеризации, который легко интерпретировать. Оговорюсь, что если число столбцов в матрице измеряется сотнями или тысячами, то, вероятно, понадобится предварительная обработка полученного результата. Но в задачах анализа результатов опросов, о чем пойдет речь ниже, обычно не требуется кластеризация по очень большому числу переменных.
Что делать, если в вашей задаче не нужно выделять группы переменных, но вы желаете получить представление о блочном виде ваших данных? Ко-кластеризация вовсе не требует обязательной группировки переменных. Как раз с такого примера мы и начнем.
Пример 1: Freedom in the World (Freedom House 2015 data)
Данные Freedom in the World (FIW) — сравнительная оценка политических прав и гражданских свобод в 195 странах мира на основе опросов экспертов проводимых организацией Freedom House. Данные за 2015 год, агрегированные до 7 под-категорий, доступны здесь.
По результатам этих 7 переменных каждой из 195 стран присваивается два рейтинга — политических прав и гражданских свобод, и итоговый статус страны — свободна, частично свободна и несвободна (всего 3 группы) по результатам этих рейтингов.
library(data.table)
library(blockcluster)
fiw.2015 <- fread("FIW 2015.csv")
fiw.2015.clusters <- cocluster(as.matrix(fiw.2015[,LETTERS[1:7],with=FALSE]),
datatype = "categorical",model = "pik_rhol_multi", nbcocluster = c(4,1),
strategy = cocluststrategy(nbinititerations=100, nbxem = 20, nbtry = 20 ))
Для объектов класса blockcluster реализована поддержка функции plot (), но я использую свой вариант отображения решения кластеризации.
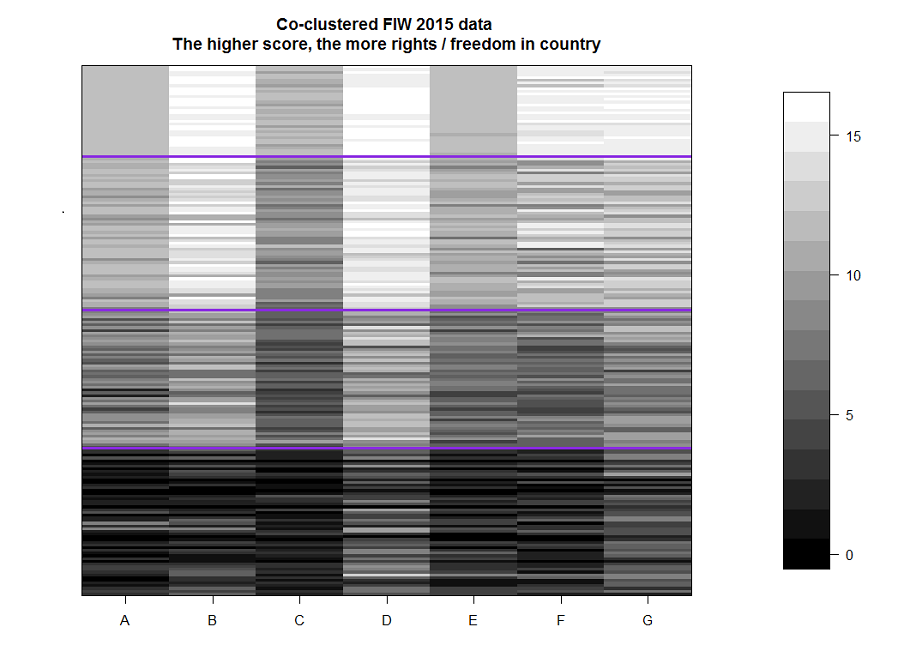
Результат кластеризации всех стран, за исключением нескольких случаев, соответствует статусу предложенному Freedom House, с поправкой на то, что 2 верхних кластера в их отчете имеют одинаковый статус — Free. Тем не менее, легко видно, что второй кластер явно отличается от первого, особенно по переменным «F» и «G». Также этот результат показывает, что в целом каждый кластер «темнее» предшествующего по всем переменным сразу. Результат блочной кластеризации представленный на географической карте в tableau public (ссылка)
В моем представлении задача кластеризации в большей степени предназначена для маркетинговых исследований, нежели социологических. Сегментирование и выделение особенностей аудиторий очень важный элемент анализа таких данных. Но в открытый доступ маркетинговые базы никто не выкладывает. Поэтому рассмотрим иллюстрацию блочной кластеризации на примере социологических данных, разумеется тип исследования на суть метода не оказывает никакого влияния.
Пример 2: Democracy module (European social survey 2012 data)
Исследования проекта ESS упоминается во всех моих предыдущих публикациях. Здесь сообщается где можно взять данные и как загрузить их в R. Мы будем группировать целевую аудиторию и переменные по блоку исследования с вопросами о демократии.
Респондентам предлагалось выставить оценки (от 0 до 10) о степени важности для демократии некоторых 16 базовых ценностей и оценить (от 0 до 10) степень применения в стране респондента 14 утверждений о гражданских институтах и правах в настоящее время. Полярные значения:
0 — «совсем не важно» / «полностью не соответствует действительности»;
10 — «крайне важно» / «полностью отвечает действительности».
Подробная информация о модуле и сами вопросы доступны по этой ссылке.
Это ссылка на pdf файл с анкетой на русском языке для респондентов из Эстонии.
Задаем целевую аудиторию: мужчины возрастом от 15 лет из Франции или России.
# block.e.names are names of Democracy module variables that were taken from questionnaire.
data <- subset(srv.data, cntry %in% c("FR", "RU") & gndr =='Male', select = c('cntry', block.e.names[1:30]))
command <- paste("data.m <- data[,as.numeric(c(",
paste(block.e.names[1:30], collapse = ","), ")) - 1]")
eval(parse(text=command))
dim(data.m) <- c(length(data.m)/30, 30)
data.clusters <- cocluster(data.m, datatype = "categorical",model = "pik_rhol_multi", nbcocluster = с(5,3),
strategy = cocluststrategy(nbinititerations=100, nbxem = 40, nbtry = 40 ))
При выводе результатов на блочную карту заменяем пропущенные значения (NA) на -5, чтобы они сильнее отличались от 0.
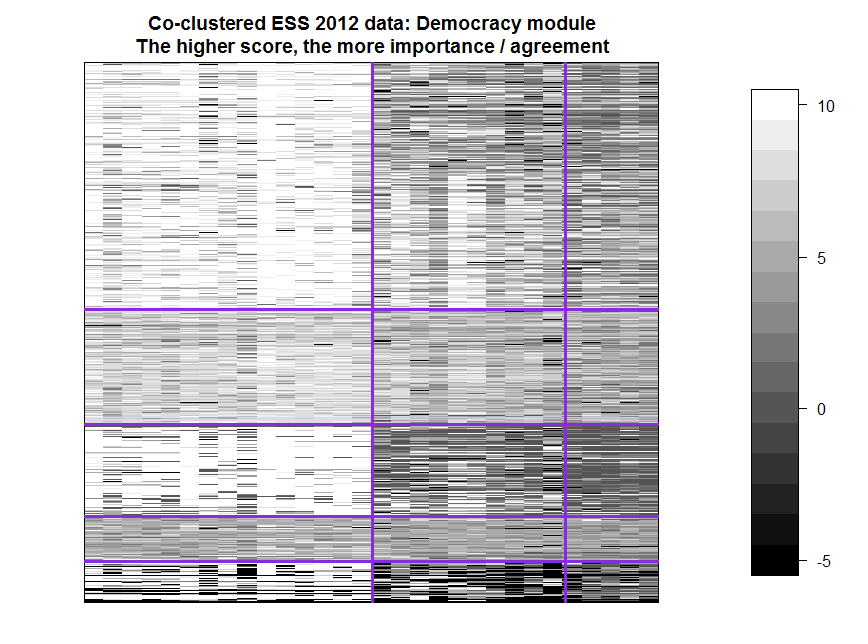
Кластеры нумеруем слева направо и сверху вниз.
Сперва о вертикальных кластерах. В первый (светлый) кластер попали первые 15 вопросов об общих (гипотетических) ценностях для демократии. Единственный из 16 вопросов о базовых ценностях для демократии не попавший в первый кластер — вопрос о консолидации («Важно ли, чтобы перед принятием решений политики учитывали мнения правительств других европейских стран»), он попал во второй кластер. Третий вертикальный кластер темнее второго в первую очередь для первого и третьего горизонтальных кластеров. Этот третий кластер состоит из следующих суждений

Те респонденты, которые подчеркивают важность для демократии базовых гражданских и политических ценностей — 1 и 3 горизонтальные кластеры, критичнее относятся к действительности — 2 и 3 вертикальные кластеры. Третий горизонтальный кластер более пессимистичен по сравнению с первым.
Горизонтальные кластеры 2 и 4 более однотонные по вертикальным составляющим, но четвертый темнее второго, особенно в первой вертикальной составляющей. Респонденты четвертого кластера не считают важным наличие каких-либо ценностей для демократической жизни страны.
В пятом горизонтальном кластере много респондентов, которые не дали ответы на ряд вопросов, большей частью из второго и первого вертикальных кластеров. Левый нижний угол очень контрастен — либо нет ответа на вопрос, либо заявляется высокая степень важности определенной ценности.
Еще о примерах. В этом pdf, в самом конце статьи, представлены примеры результатов блочной кластеризации изображения и текстов аннотаций научных статей.
Литература:
[1] G. Govaert, M. Nadif, Block clustering with Bernoulli mixture models: Comparison of different approaches, Computational Statistics & Data Analysis, Volume 52, Issue 6, 20 February 2008, Pages 3233–3245.
[2] C. Ding et al. Orthogonal nonnegative matrix t-factorizations for clustering //Proceedings of the 12th ACM SIGKDD international conference on Knowledge discovery and data mining. — ACM, 2006. — С. 126–135.
[3] C. Keribin et al. Estimation and selection for the latent block model on categorical data //Statistics and Computing. — 2014. — С. 1–16.
[4] P.S. Bhatia et al. blockcluster: Coclustering package for binary, contingency, continuous and categorical data-sets. R package version 3.0.2
