Книга «Тайная жизнь программ. Как создать код, который понравится вашему компьютеру»27.06.2023 17:47

Привет, Хаброжители!

Знакомы ли вы с технологиями, лежащими в основе вашей собственной программы? Почему «правильный» код не хочет работать? Истина проста и банальна — нужно сразу создавать код, который будет работать хорошо и не будет прятать в себе трудноуловимые ошибки.
Для этого Джонатан Стейнхарт исследует фундаментальные концепции, лежащие в основе работы компьютеров. Он рассматривает аппаратное обеспечение, поведение программ на определенных устройствах, чтобы показать, как на самом деле должен работать ваш код.

Узнайте, что на самом деле происходит, когда вы запускаете код на компьютере, — и вы научитесь программировать лучше и эффективнее.

Рекурсивное деление

Я мельком коснулся темы рекурсивного деления в разделе «Стеки» на с. 166. В этом разделе мы рассмотрим эту широко используемую технику более подробно и узнаем, как она помогает сократить объем выполняемой работы.

Спирали

Код для рисования линий, который мы написали ранее, можно изменить так, чтобы рисовать более сложные линии путем нанесения на сетку нескольких точек и их соединения.

Наверняка из школьных уроков математики вы помните что-то об измерении углов в градусах и о том, что полный круг составляет 360 градусов. Помимо градусов, существуют и другие системы измерения углов, например радианы. Круг соответствует 2π радианам. Соответственно, 360 градусов — это 2π радиан, 180 градусов — π радиан, 90 градусов — π/2 радиан, 45 градусов — π/4 радиан и т. д. Я так подробно говорю об этом сейчас потому, что многие тригонометрические функции из математических библиотек, в том числе в JavaScript, подразумевают измерение углов в радианах, а не в градусах.

В наших примерах мы будем использовать кривые, нарисованные в полярной системе координат, — просто потому, что они красиво выглядят. На всякий случай упомяну, что в полярной системе координат используются радиус r и угол θ вместо x и y. Значения легко перевести в декартову систему координат: x = r cosθ и y = rsinθ. В первом примере нарисуем спираль при помощи уравнения r = θ × 10. Рисуемая точка удаляется от центра по мере изменения углов. Большинству людей нелегко переключиться в уме с градусов на радианы, поэтому для примера используем входные данные в градусах. В листинге 11.13 представлена разметка для элементов управления.

Листинг 11.13. Разметка для элементов управления спиралью

  Градусы: 
  
  Нарисовать
  Стереть

Вместо кода для рисования сетки уделим внимание другим деталям. В листинге 11.14 точка с координатами (0, 0) представляет собой центр спирали, поскольку мы используем полярную систему координат.

Листинг 11.14. Рисование спирали из точек в JavaScript

canvas.scale(1, -1);
canvas.translate(width / 2, -height / 2);
$('#erase').click(function() {
  canvas.clearRect(-width, -height, width * 2, height * 2);
});

$('#draw').click(function() {
  if (parseFloat($('#degrees').val()) == 0)
    alert('Градусы должны быть больше 0');
  else {
    for (var angle = 0; angle < 4 * 360; angle += parseFloat($('#degrees').val())) {
      var theta = 2 * Math.PI * angle / 360;
      var r = theta * 10;
      canvas.beginPath();
      canvas.arc(r * Math.cos(theta), r * Math.sin(theta), 3, 0, 2 * Math.PI, 0);
      canvas.fill();
    }
  }
});

Введите 10 (значение в градусах) и нажмите кнопку «Нарисовать». В результате должно получиться изображение, как на рис. 11.15.

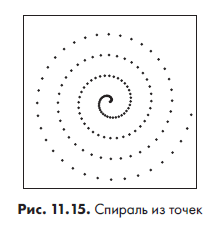
Обратите внимание, что по мере удаления от центра спирали расстояние между точками становится все больше — в самом центре точки даже перекрывают друг друга. Можно ввести очень маленькое значение и получить практически идеальную кривую, но в этом случае точки перекроют друг друга еще больше. Рисование займет больше времени, и будет сложнее рассчитать значения произвольной функции.

Попробуем соединять точки линиями — замените фрагмент кода для рисования спирали на код из листинга 11.15.

Листинг 11.15. Рисуем спираль, соединяя точки линиями в JavaScript

canvas.beginPath();
canvas.moveTo(0, 0);

for (var angle = 0; angle < 4 * 360; angle += parseFloat($('#degrees').val())) {
  var theta = 2 * Math.PI * angle / 360;
  var r = theta * 10;
  canvas.lineTo(r * Math.cos(theta), r * Math.sin(theta));
}
canvas.stroke();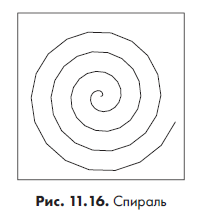

Введите 20 (значение в градусах) и нажмите кнопку «Нарисовать». Результат показан на рис. 11.16.

Спираль все еще не очень ровная. Опять же, она неплохо выглядит в центре, но ближе к краям линия становится все менее и менее плавной. Нужно найти способ вычислять координаты для дополнительных точек — и для этого пригодится уже знакомое рекурсивное деление. Сейчас мы рисуем линии, используя функцию для спирали между двух углов, θ1 и θ2, — вместо этого будем опираться на некоторый критерий достаточной близости. Он означает, что, если две точки не находятся достаточно близко друг к другу, мы будем делить разницу между углами пополам и заново проверять критерий, пока не найдем достаточно близкую точку. Используем формулу

чтобы рассчитать расстояние между точками, как показано в листинге 11.16.

Листинг 11.16. Рекурсивное рисование спиральной линии в JavaScript

var close_enough = 10;

function
plot(theta_1, theta_2)
{
  var r;

  r = theta_1 * 10;
  var x1 = r * Math.cos(theta_1);
  var y1 = r * Math.sin(theta_1);

  r = theta_2 * 10;
  var x2 = r * Math.cos(theta_2);
  var y2 = r * Math.sin(theta_2);

  if (Math.sqrt(((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1))) < close_enough) {
    canvas.moveTo(x1, y1);
    canvas.lineTo(x2, y2);
  }
  else {
    plot(theta_1, theta_1 + (theta_2 - theta_1) / 2);
    plot(theta_1 + (theta_2 - theta_1) / 2, theta_2);
  }
}

$('#draw').click(function() {
  if (parseFloat($('#degrees').val()) == 0)
    alert('Градусы должны быть больше 0');
  else {
    canvas.beginPath();

    for (var angle = 0; angle < 4 * 360; angle +=
                        parseFloat($('#degrees').val())) {
      var old_theta;
      var theta = 2 * Math.PI * angle / 360;
      if (angle > 0)
        plot(old_theta, theta);
      old_theta = theta;
    }
  }

  canvas.stroke();
});

Пока значение переменной close_enough достаточно мало, увеличение значения в градусах несущественно, поскольку код автоматически сгенерирует нужное количество промежуточных углов. Попробуйте ради интереса подставить разные значения переменной close_enough. Для удобства добавьте в разметку соответствующее поле ввода.

В некоторых случаях определение достаточной близости весьма важно. Хотя это и выходит за рамки данной книги, вспомните, как в кино выглядят разные изогнутые объекты — при хорошей подсветке они кажутся более реалистичными. Теперь представьте зеркальную сферу, которую можно условно разбить на некоторое количество плоских граней. Наша спираль также разбивается на несколько отрезков. Если плоские грани слишком большие, вместо сферы мы получим что-то вроде диско-шара, который будет отражать свет совсем иначе.

Конструктивная геометрия

В главе 5 я кратко упомянул квадродеревья, или деревья квадрантов, показав, как с их помощью можно представлять различные формы. Они, очевидно, используют рекурсию вкупе с иерархическим механизмом разделения пространства.

Над квадродеревьями можно выполнять булевы операции. Например, нам нужно спроектировать что-то вроде прокладки ГБЦ (головки блока цилиндров) в двигателе автомобиля, как на рис. 11.17.

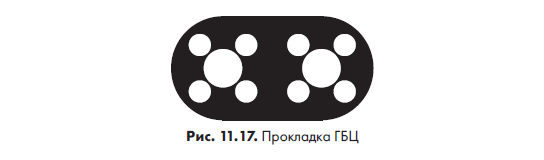
Для узла квадродерева нам понадобятся структура данных и два специальных значения листьев: один — для 0 (белый цвет на рисунке), второй — для 1 (черный цвет). На рис. 11.18 показана подобная структура данных. Каждый узел ссылается на четыре других узла — хороший пример использования указателей в языках наподобие С.

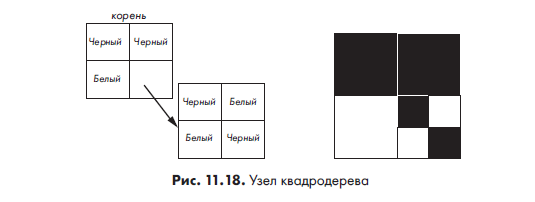
В данном случае размер узла неважен. Все операции начинаются с корня дерева заданного размера, а каждый дочерний узел имеет размер, равный четверти родительского узла. На рис. 11.19 представлена схема для получения значения выбранного узла дерева.

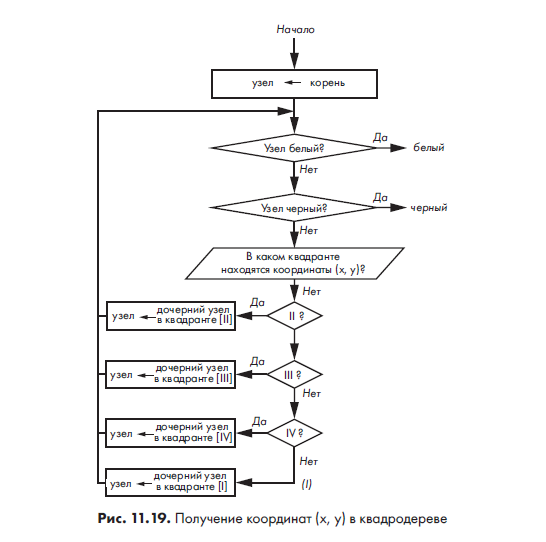
На рис. 11.20 показано, как задаются значения (то есть обозначаются черным цветом) для точек квадродерева с координатами (x, y). «Выполнено» означает «выход из функции», так как функция рекурсивная.

Подобным образом мы получали координаты точки на рис. 11.19. Алгоритм проходит по дереву в направлении сверху вниз, до тех пор пока не достигнет квадрата размером 1 × 1 с координатами (x, y) и не окрасит его в черный цвет. Если на пути встречается узел белого цвета, алгоритм заменяет его на новый узел с четырьмя дочерними узлами белого цвета. Таким образом создается дерево для продвижения сверху вниз. На обратном пути вверх все узлы с дочерними узлами черного цвета заменяются на отдельный черный узел. Это происходит каждый раз, когда в узле с тремя дочерними узлами черного цвета последний белый дочерний узел меняет цвет на черный, как показано на рис. 11.21.

Объединение узлов не только экономит память для хранения дерева, но и положительно сказывается на скорости операций, поскольку глубина дерева уменьшается.

Нужно найти способ очистить (то есть окрасить в белый цвет) значение координаты (x, y) в квадродереве. Решение этой задачи очень похоже на уже известный нам алгоритм задания цвета. Разница заключается в том, что теперь разделяются не белые, а черные узлы, а белые — наоборот, объединяются.

На основе функции задания значения можно создавать более сложные функции рисования. К примеру, задав необходимые координаты точек, можно нарисовать прямоугольник. Эта же функция пригодится и при рисовании эллипсов — мы лишь добавим принципы симметрии и алгоритм из раздела «Кривые линии» на с. 362.

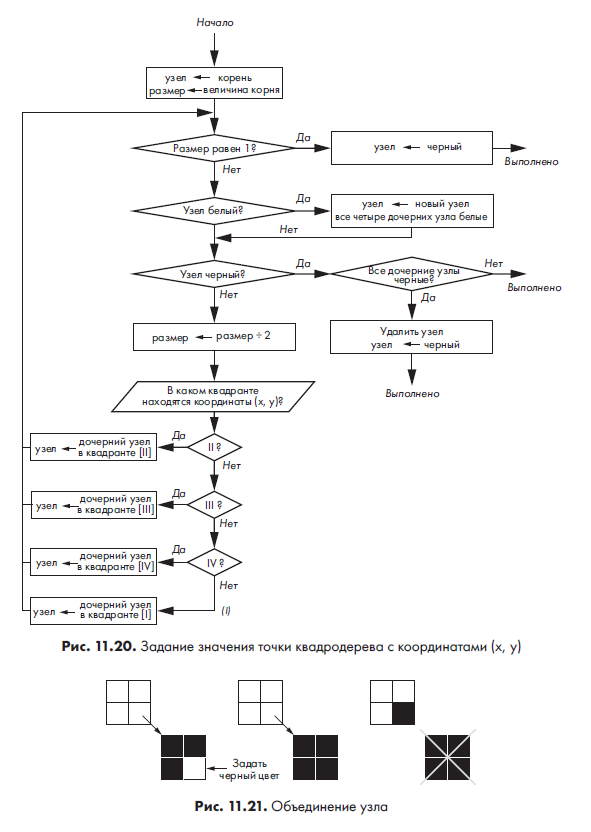
Забавы ради напишем версии функций булевой логики из главы 1 для квад­родеревьев. Функция НЕ самая простая: спускаемся по дереву и заменяем все черные узлы белыми, а все белые — черными. Функции И и ИЛИ на рис. 11.22 требуют больше внимания. Эти алгоритмы не предназначены для вычисления эквивалентов выражений C = a AND b и C = a OR b. Вместо этого вычисляются выражения dst & = src и dst |= src, как в случае с используемыми во многих языках операторами присваивания. При этом изменяется только операнд dst.

Собрав все инструменты, перейдем к созданию прокладки ГБЦ. Разрешение возьмем низкое, чтобы были видны все детали. Начнем с квадродерева для пустой прокладки слева и начального квадродерева в центре, где нарисуем большой круг. Начальное квадродерево соединяется с прокладкой при помощи операции ИЛИ, в результате чего получим вариант справа на рис. 11.23. Обратите внимание: количество делений сведено к минимуму благодаря объединению узлов.

Создадим новый круг в другом месте и объединим его с начальной версией прокладки, как показано на рис. 11.24.

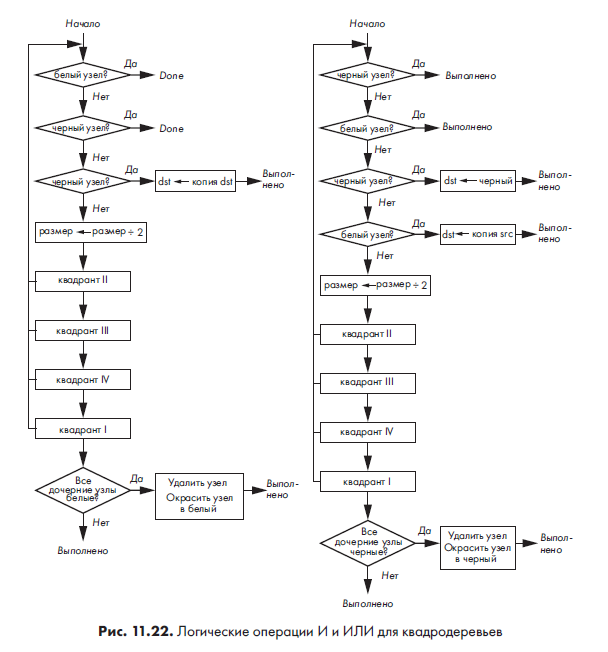
Продолжим, создав черный прямоугольник и объединив его с прокладкой, как показано на рис. 11.25.

Следующий шаг — проделать в прокладке отверстие. Для этого нужно создать черный круг, а затем инвертировать его при помощи операции НЕ, получив круг белого цвета. Результат объединим с текущей версией прокладки, воспользовавшись операцией И. Так мы получим прокладку с отверстием, как показано на рис. 11.26.

К этому моменту уже может стать скучно. Тем же способом нужно добавить еще одно отверстие, как на рис. 11.26, и восемь новых мелких отверстий. Результат показан на рис. 11.27.

Как видим, в квадродеревьях мы использовали булевы функции, чтобы создать объекты сложной формы из геометрически простых частей. В примере мы ограничились двумерной прокладкой, но обычно такие вещи создаются в трех измерениях. Для трех измерений понадобится в два раза больше узлов, поэтому вместо квадродерева мы перейдем к октодереву, пример которого изображен на рис. 11.28.

Построение сложных трехмерных объектов на основе рассмотренных техник называется конструктивной блочной геометрией. Трехмерный аналог двумерного пикселя называется воксел (voxel — сокращение от volume pixel («объемный пиксель»)).

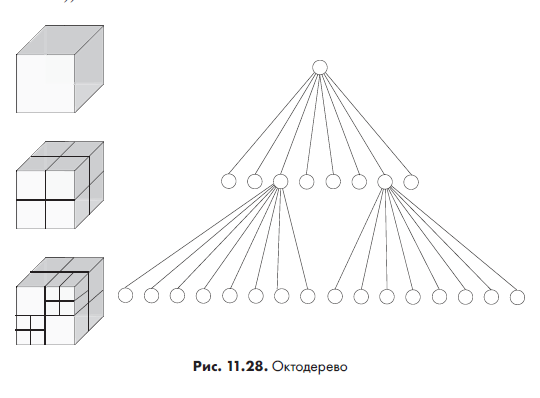
Октодеревья часто используются для хранения данных, полученных от аппаратов компьютерной томографии и МРТ. Эти устройства генерируют стопки 2D-срезов, которые легко разделить, тем самым получив нужный вид в разрезе.

Сдвиг и наложение масок

Один из недостатков квадродеревьев — расположение данных в памяти. Данные разбросаны по разным уголкам памяти, и отследить их местоположение очень сложно. Даже если два узла квадродерева находятся рядом друг с другом, это не означает, что в памяти они расположены так же близко. Особенно остро эта проблема проявляется, когда нужно перевести данные из одной системы организации памяти в другую. Конечно, всегда можно перенести данные бит за битом, но для этого потребуется очень часто обращаться к памяти. Такой способ займет много времени, и потому он нам не подходит.

С подобной проблемой можно встретиться при выведении данных на экран. Организация памяти экрана зависит от аппаратного обеспечения. Как я уже упоминал в разделе «Растровая графика» на с. 230, каждый ряд растрового изображения рисуется на экране последовательно, в заданном порядке. Растровый ряд называется строкой развертки, а весь набор строк развертки — кад­ровым буфером.

Предположим, что нам нужно вывести изображение готовой прокладки ГБЦ на экран компьютера. Простоты ради ограничимся монохромным дисплеем с памятью шириной в 16 бит из расчета 1 бит на 1 пиксель. Это означает, что верхние левые 16 пикселей будут относиться к первому слову, следующие 16 пикселей — ко второму и т.д.

Квадрат слева вверху на рис. 11.27 имеет размеры 4×4 пикселя и окрашен в белый цвет — то есть нужно очистить биты кадрового буфера. Будем использовать координаты и размер квадрата в квадродереве для создания маски, как показано на рис. 11.29.

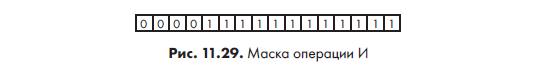
Затем к полученной маске и всем связанным рядам можно применить операцию И, для чего потребуется всего по два обращения к памяти для каждого ряда: одно — для чтения, второе — для записи. Нечто подобное выполним и для битов кадрового буфера, только в этом случае маска будет содержать единицы, и мы применим операцию ИЛИ вместо И.

Еще один пример, где может пригодиться данный алгоритм, — рисование текстовых символов. Большинство текстовых символов хранятся в виде битовых мат­риц — двумерных массивов битов, как показано на рис. 11.30. Битовые матрицы нескольких символов объединяются и хранятся вместе в целях экономии памяти. Ранее все текстовые символы были организованы таким образом, сейчас же мы перешли к использованию геометрических описаний. Однако ради улучшения производительности описания символов часто переводятся в битовые матрицы перед использованием, и повторно используемые символы кэшируются.

Заменим изображенный выше символ B на C, как показано на рис. 11.31.

Символ C хранится в битах 10–14, и теперь его нужно переместить в биты 6–10. Для этого потребуется взять символ C в каждом ряду и наложить маску на оставшиеся символы в слове. Затем необходимо сдвинуть символ C в заданную позицию. Место назначения должно быть прочитано, а на перезаписываемые позиции предварительно должна быть наложена маска. Затем сдвинутый символ C объединяется с остальными позициями и записывается, как показано на рис. 11.32.

В данном примере на каждый ряд приходится три обращения к памяти: одно — для получения источника, второе — для получения места назначения, третье — для записи результата. Если выполнять все то же самое с каждым отдельным битом, это займет в пять раз больше времени.

В некоторых случаях могут возникнуть дополнительные сложности — например, если символ переносится за границы начального слова.

Более подробно с книгой можно ознакомиться на сайте издательства:
» Оглавление
» Отрывок

По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
Для Хаброжителей скидка 25% по купону — Код

© Habrahabr.ru