Книга «Совершенный алгоритм. Графовые алгоритмы и структуры данных»
 Привет, Хаброжители! Алгоритмы — это сердце и душа computer science. Без них не обойтись, они есть везде — от сетевой маршрутизации и расчетов по геномике до криптографии и машинного обучения. «Совершенный алгоритм» превратит вас в настоящего профи, который будет ставить задачи и мастерски их решать как в жизни, так и на собеседовании при приеме на работу в любую IT-компанию.
Привет, Хаброжители! Алгоритмы — это сердце и душа computer science. Без них не обойтись, они есть везде — от сетевой маршрутизации и расчетов по геномике до криптографии и машинного обучения. «Совершенный алгоритм» превратит вас в настоящего профи, который будет ставить задачи и мастерски их решать как в жизни, так и на собеседовании при приеме на работу в любую IT-компанию.
Во второй книге Тим Рафгарден — гуру алгоритмов — расскажет о графовом поиске и его применении, алгоритме поиска кратчайшего пути, а также об использовании и реализации некоторых структур данных: куч, деревьев поиска, хеш-таблиц и фильтра Блума.
В данном посте представлен отрывок «Фильтры Блума: основы»
О чем эта книга
Вторая часть книги «Совершенный алгоритм» — это вводный курс в основы грамотности по следующим трем темам.
Графовый поиск и приложения. Графы моделируют ряд разных типов сетей, включая дорожные, коммуникационные, социальные сети и сети зависимостей между задачами. Графы могут быть сложными, однако существует несколько невероятно быстрых примитивов для рассуждения о структуре графа. Мы начнем с линейно-временных алгоритмов графового поиска, с приложений в диапазоне от сетевого анализа до построения последовательности выполнения операций.
Кратчайшие пути. В задаче о кратчайшем пути цель состоит в том, чтобы вычислить наилучший маршрут в сети из точки A в точку B. Данная задача имеет очевидные применения, такие как вычисление маршрутов движения, а также встречается в замаскированном виде во многих других универсальных задачах. Мы обобщим один из наших алгоритмов графового поиска и придем к знаменитому алгоритму поиска кратчайшего пути Дейкстры.
Структуры данных. Эта книга сделает вас высокообразованным пользователем нескольких разных структур данных, предназначенных для поддержания эволюционирующего множества объектов с ассоциированными с ними ключами. Основная цель состоит в развитии интуиции о том, какая структура данных является правильной для вашего приложения. Дополнительные разделы содержат рекомендации по реализации этих структур данных с нуля.
Сначала мы обсудим кучи, которые могут быстро идентифицировать хранимый объект с наименьшим ключом, а также полезны для сортировки, реализации очереди с приоритетом и реализации почти линейно-временного алгоритма Дейкстры. Деревья поиска сохраняют полную упорядоченность ключей хранимых объектов и поддерживают еще более широкий спектр операций. Хеш-таблицы оптимизированы для сверхбыстрых операций поиска и широко распространены в современных программах. Мы также рассмотрим фильтр Блума, близкого родственника хеш-таблицы, который использует меньше пространства за счет случайных ошибок.
Более подробно ознакомиться с содержанием книги можно в разделах «Выводы», которые завершают каждую главу и вычленяют наиболее важные моменты. Разделы книги, помеченные звездочкой, являются наиболее продвинутыми по уровню изложенной информации. Если книга рассчитана на поверхностное ознакомление с темой, то читатель может пропустить их без потери целостности написанного.
Темы, затронутые в трех других частях. Первая часть книги «Совершенный алгоритм. Основы» охватывает асимптотические обозначения (форму записи О-большое и ее близких родственников), алгоритмы «разделяй и властвуй» и основную теорему о рекуррентных соотношениях — основной метод, рандомизированную быструю сортировку и ее анализ, а также линейно-временные алгоритмы отбора. В третьей части речь идет о жадных алгоритмах (планирование, минимальные остовные деревья, кластеризация, коды Хаффмана) и динамическом программировании (задача о рюкзаке, выравнивание последовательности, кратчайшие пути, оптимальные деревья поиска). Четвертая часть посвящена NP-полноте, тому, что она означает для проектировщика алгоритмов, и стратегиям решения вычислительно неразрешимых задач, включая эвристический анализ и локальный поиск.
12.5. Фильтры Блума: основы
Фильтры Блума являются близкими родственниками хеш-таблиц. Они очень компактны, но взамен периодически делают ошибки. В данном разделе дается описание того, чем хороши фильтры Блума и как они реализуются, в то время как раздел 12.6 излагает кривую компромисса между объемом используемого фильтром пространства и его частотой ошибок.
12.5.1. Поддерживаемые операции
Причина существования фильтров Блума по существу такая же, как и у хеш-таблицы: сверхбыстрые операции вставки и просмотра, благодаря которым вы можете быстро вспомнить, что вы видели, а что нет. Почему нас должна беспокоить другая структура данных с тем же множеством операций? Потому что фильтры Блума предпочтительнее хеш-таблиц в приложениях, в которых пространство ценится на вес золота, и случайная ошибка не является помехой для сделки.
Как и хеш-таблицы с открытой адресацией, фильтры Блума гораздо проще реализовать и представить в уме, когда они поддерживают только операции Вставить и Просмотреть (и без операции Удалить). Мы сосредоточимся на этом случае.
ФИЛЬТРЫ БЛУМА: ПОДДЕРЖИВАЕМЫЕ ОПЕРАЦИИПросмотреть: по ключу k вернуть «да», если k был ранее вставлен в фильтр Блума, и «нет» — в противном случае.
Вставить: добавить новый ключ k в фильтр Блума.
Фильтры Блума являются очень пространственно-эффективными; в типичном случае они могут потребовать всего 8 бит на вставку. Это довольно невероятно, так как 8 бит совершенно недостаточно, для того чтобы запомнить даже 32-битный ключ или указатель на объект! По этой причине операция Просмотреть в фильтре Блума возвращает только ответ «да» / «нет», тогда как в хеш-таблице данная операция возвращает указатель на искомый объект (если он найден). Именно поэтому операция Вставить теперь принимает только ключ, а не (указатель на) объект.
В отличие от всех других изученных нами структур данных фильтры Блума могут ошибаться. Существует два вида ошибок: ложные отрицания, когда операция Просмотреть возвращает «ложь», даже если запрашиваемый ключ был уже вставлен ранее, и ложные утверждения (или срабатывания), когда операция Просмотреть возвращает «истину», хотя запрашиваемый ключ еще не был вставлен в прошлом. В разделе 12.5.3 мы увидим, что базовые фильтры Блума никогда не страдают от ложных отрицаний, но они могут иметь «фантомные элементы» в виде ложных утверждений. В разделе 12.6 показано, что частотой ложных утверждений можно управлять, соответствующим образом настраивая использование пространства. Типичная реализация фильтра Блума может иметь частоту ошибок около 1% либо 0,1%.
Времена выполнения операций Вставить и Просмотреть являются такими же быстрыми, как и в хеш-таблице. И даже лучше, эти операции гарантированно выполняются в постоянном времени, независимо от реализации фильтра Блума и набора данных1. Однако реализация и набор данных влияют на частоту ошибок фильтра.
Подведем итоги преимуществ и недостатков фильтров Блума над хеш-таблицами:
ФИЛЬТР БЛУМА ПРОТИВ ХЕШ-ТАБЛИЦЫ1. Плюсы: более пространственно-эффективный.
2. Плюсы: гарантированно постоянно-временные операции для каждой совокупности данных.
3. Минусы: не может хранить указатели на объекты.
4. Минусы: более сложные удаления в сравнении с хеш-таблицей со сцеплением.
5. Минусы: ненулевая вероятность ложного утверждения.
Перечень показателей для базовых фильтров Блума выглядит следующим образом.
Таблица 12.4. Базовые фильтры Блума: поддерживаемые операции и время их выполнения. Знак кинжала (†) указывает на то, что операция Просмотреть имеет управляемую, но ненулевую вероятность ложных утверждений

Фильтры Блума следует использовать вместо хеш-таблиц в приложениях, в которых имеют значение их преимущества, а их недостатки не являются помехой для сделки.
КОГДА ИСПОЛЬЗОВАТЬ ФИЛЬТР БЛУМАЕсли приложению требуется быстрый поиск с динамически эволюционирующим множеством объектов, пространство ценится на вес золота и приемлемо малое число ложных утверждений, то фильтр Блума обычно является предпочтительной структурой данных.
12.5.2. Применения
Далее идут три применения с повторными просмотрами, где экономия пространства может быть важной, а ложные утверждения не являются помехой для сделки.
Спеллчекеры. Еще в 1970-х годах фильтры Блума использовались для реализации средств проверки орфографии — спеллчекеров. На этапе предобработки каждое слово в словаре вставляется в фильтр Блума. Орфографическая проверка документа сводится к одной операции Просмотреть на слово в документе, помечая любые слова, для которых данная операция возвращает «нет».
В этом приложении ложное утверждение соответствует недопустимому слову, которое спеллчекер непреднамеренно принимает. Такие ошибки не делали спеллчекеры идеальными. Однако в начале 1970-х годов пространство ценилось на вес золота, поэтому в то время использование фильтров Блума было беспроигрышной стратегией.
Запрещенные пароли. Старое приложение, которое остается актуальным до сего дня, отслеживает запрещенные пароли — пароли, которые слишком распространены либо их слишком легко угадать. Изначально все запрещенные пароли вставляются в фильтр Блума; дополнительные запрещенные пароли могут быть вставлены позже, по мере необходимости. Когда пользователь пытается установить либо сбросить свой пароль, то система ищет предложенный пароль в фильтре Блума. Если поиск возвращает «да», то пользователю предлагается повторить попытку с другим паролем. Здесь ложное утверждение транслируется в прочный пароль, который система отклоняет.
При условии, что частота ошибок не слишком велика, скажем не более 1% либо 0,1%, это не имеет большого значения. Время от времени некоторым пользователям потребуется одна дополнительная попытка найти пароль, приемлемый для системы.
Интернет-маршрутизаторы. Ряд сногсшибательных сегодняшних применений фильтров Блума имеют место в глуби интернета, где пакеты данных проходят через маршрутизаторы с потоковой скоростью. Существует много причин, почему маршрутизатор мог бы захотеть быстро вспомнить то, что он видел в прошлом. Например, маршрутизатор может захотеть найти истоковый IP-адрес пакета в списке заблокированных IP-адресов, отследить содержимое кэша, для того чтобы избежать паразитных просмотров кэша, или вести статистику, помогающую в идентификации сетевой атаки «отказ в обслуживании». Скорость поступления пакетов требует сверхбыстрых просмотров, а ограниченная память маршрутизатора делает пространство на вес золота. Эти применения находятся в прямом ведении фильтра Блума.
12.5.3. Реализация
Заглянув внутрь фильтра Блума, можно увидеть элегантную реализацию. Структура данных поддерживает n-битовую строку или, равным образом, массив A длины n, в котором каждый элемент равен 0 или 1. (Все элементы инициализируются нулем.) Данная структура также использует m хеш-функций h1, h2, …, hm, при этом каждая отображает универсум U всех возможных ключей в множество {0, 1, 2, …, n — 1} позиций в массиве. Параметр m пропорционален числу бит, используемых фильтром Блума для вставки, и, как правило, является малой константой (например, 5).
Всякий раз, когда ключ вставляется в фильтр Блума, каждая из m хеш-функций ставит флаг, устанавливая соответствующий бит массива A равным 1.
ФИЛЬТР БЛУМА: ВСТАВИТЬ (ПО КЛЮЧУ k)for i = 1 to m do A[hi(k)] := 1
Например, если m = 3 и h1(k) = 23, h2(k) = 17 и h3(k) = 5, вставка k приводит к тому, что 5-й, 17-й и 23-й биты массива устанавливаются равными 1 (рис. 12.5).

В операции Просмотреть фильтр Блума отыскивает отпечаток, который мог бы остаться при вставке k.
ФИЛЬТР БЛУМА: ПРОСМОТРЕТЬ (ПО КЛЮЧУ k)for i = 1 to m do if A [hi (k)] = 0 then return «нет» return «да»
Теперь мы можем увидеть, почему фильтры Блума не могут страдать от ложных отрицаний. Когда ключ k вставляется, соответствующие m бит устанавливаются равными 1. За время жизни фильтра Блума биты могут менять свое значение с 0 на 1, но не наоборот. Тем самым эти m бит остаются 1 навсегда. Каждая последующая операция Просмотреть k гарантированно возвращает правильный ответ «да».
Мы также можем увидеть, как возникают ложные утверждения. Предположим, что m = 3 и четыре ключа k1, k2, k3, k4 имеют следующие хеш-значения:
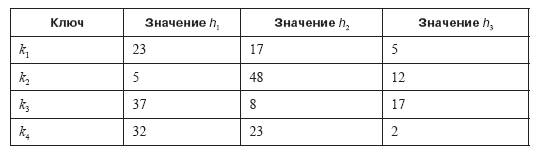
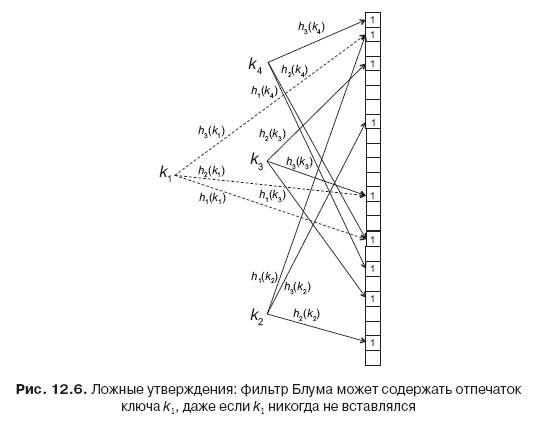
Предположим, что мы вставляем k1, k2, k3 и k4 в фильтр Блума (рис. 12.6). Эти три вставки в общей сложности приводят к тому, что девять бит устанавливаются равными 1, включая три бита в отпечатке ключа k1 (5, 17 и 23). На этом этапе фильтр Блума больше не может различать, был или нет вставлен ключ k1. Даже если k1 не был вставлен в фильтр, поиск вернет «да», что является ложным утверждением.
Интуитивно можно предположить, что с увеличением размера n фильтра Блума число наложений между отпечатками разных ключей должно уменьшаться, что, в свою очередь, приводит к меньшему числу ложных утверждений. Но первоочередная цель фильтра Блума — экономить пространство. Существует ли золотая середина, где и n, и частота ложных утверждений одновременно малы? Ответ не очевиден и требует некоторого математического анализа, предпринятого в следующем далее разделе.
» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 20% по купону — Алгоритмы
По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
