Классические алгоритмы генерации лабиринтов. Часть 2: погружение в случайность

Предисловие
→ Первая часть
Итак. Оценив отклик аудитории Хабра и разобравшись с делами, я принялся за написание второй статьи из цикла. Реакция публики оказалась значительно позитивнее моих предположение, а значит, мы продолжаем разговор на одну из любопытнейших тем процедурной генерации — создание лабиринтов.
В этой части мы поговорим о том, что же такое случайная и псевдослучайная генерации, какие алгоритмы могут дать нам равновероятно ничем не похожие друг на друга лабиринты и в чем их минусы. Героями нашего сегодняшнего приключения станут алгоритм Уилсона и алгоритм Олдоса-Бродера для создания случайного остовного дерева (Uniform Spanning Tree). ОСТОРОЖНО ТРАФИК.
Давайте вспомним, что такое идеальные лабиринты, о которых идет речь. Если из каждой вершины графа в любую другую имеется ровно один путь и нельзя пройти все вершины, не пройдя по одному и тому же ребру дважды, то мы называем такой граф остовным деревом. Если в рассматриваемом лабиринте из каждой клетки в любую другую имеется ровно один проход и нельзя посетить все клетки, не пройдя через один и тот же коридор дважды, то мы говорим, что такой лабиринт идеальный. Смысл не меняется по одной простой причине — лабиринты и есть графы, о чём я писал в прошлой статье. Если Вы её ещё не читали, настоятельно советую пролистать немного выше, перейти по ссылке и ознакомиться с ней, прежде чем идти дальше.
И хотя представленные в этой части алгоритмы весьма медленные и «глупые», с ними необходимо разобраться, так как они являют собой фундамент для всей нашей темы и для всех моих статей. Главная причина, почему я сразу не начал с них — Уилсон не очень прост в реализации и понимании для начинающих, что не мешает быть ему крайне любопытным.
Позволяет программе получить все поля таблицы. Первый параметр — это таблица, второй — индекс в этой таблице. next возвращает следующий индекс в таблице и соответствующее ему значение. Если второй параметр nil, next возвращает начальный индекс и связанное с ним значение. При вызове последнего индекса, или с nil в пустой таблице, next возвращает nil. Если второй параметр отсутствует, он интерпретируется как nil. В частности, Вы можете использовать next (t) для проверки пустая таблица или нет.
Следовательно, вместо того, чтобы выбирать клетку с помощью math.random и проверять, обработана ли она или использовать связку стэк-клеток вместе с хэш-таблицей для отслеживания местоположения в нем, можно использовать лишь одну хэш-таблицу, ключи в которой будут захэшироваными координатами и брать элементы из неё с помощью next.
key = next(cellsHash, nil)
local start_x, start_y = aux.deHashKey(key)
cellsHash[key] = nil — Напомню, присваивание nil удаляет элемент/полеСмещение и случайность
Что мы подразумеваем под случайной генерацией? Можем ли мы сказать, что если во втором лабиринте, в отличии от первого, отсутствует две стенки на юге, то они полностью случайны? Или если первый лабиринт имеет на два горизонтальных коридора больше? И да, и нет.
Говоря о случайности в лабиринтах, мы должны четко осознавать, что имеем в виду. Давайте посмотрим на результат работы алгоритма двоичного дерева:


Как видим, хотя лабиринты сами по себе совершенно разные, смещение у них практически идентичное. Разница лишь в нескольких коротких горизонтальных проходах в правой половине.
Мы получили случайный результат? Да. Можем ли мы его таковым считать? Ну, по-моему мнению, нет.
Проблема в смещении (bias), которое во многом определяет «случайность». Алгоритмы, которые по определению должны создавать случайные лабиринты, в итоге создают похожие. Если «похожесть» ярко выражена, как в двоичном дереве, мы говорим, что такой лабиринт легко решается. Если же при сравнении нескольких лабиринтов нам трудно однозначно сказать, к чему тяготеет алгоритм, мы говорим, что такой лабиринт решается сложнее. Для нахождения смещение, нам нужно сравнить несколько результатов генерации и построить статистическую модель, по которой бы мы могли написать более умный поиск пути или самим, «более умно» решать лабиринты такого типа. Например, мы можем сказать, что алгоритм двоичного дерева имеет в n раз больше горизонтальных проходов, чем вертикальных. Значит, можно будет учесть данные и ускорить процесс нахождения выхода.
А что если мы хотим, чтобы смещения вообще не было? Чтобы из, к примеру, 9 не связанных точек графа, каждый раз мы получали совершенно непохожее на остальные остовное дерево? Тогда нам нужно, чтобы каждое из направлений для алгоритма было равноценно. Значит, мы разрешаем проходить по уже пройденным вершинам, следовательно, в каждой итерации цикла будем случайно выбирать одно из четырех направлений вне зависимости от того, были ли мы там или нет. Единственное условие — не выходить за рамки поля.
К слову о термине Uniform Spanning Tree. Мы уже знаем, что такое остовное дерево. Соединив все вершины графа ребрами так, чтобы из любой вершины в другую нельзя было попасть, не пройдя одно и то же ребро дважды, мы получим остовное дерево. Но ведь если вершин в графе более двух, то и вариаций деревьев может быть больше, верно? Так вот, Uniform Spanning Tree — одна равновероятно выбранная вариация остовного дерева в некотором графе.
И так. Мы хотим совершенно случайные, совершенно непохожие друг на друга лабиринты, и даже готовы пожертвовать скоростью. Тогда давайте познакомимся с алгоритмами Олдоса-Бродера и Уилсона.
Алгоритм Олдоса-Бродера



Описание
Помните я говорил, что алгоритм двоичного дерева самый простой в понимании? Так вот, я лукавил. Он действительно проще в реализации, так как там мы имеем дело всегда только с одним направлением и c одним рассматриваемым рядом, но в примитивности и «глупости» алгоритм Олдоса-Бродера ушел далеко вперед. Весь его смысл заключается в том, чтобы бесцельно блуждать по полю в надежде наткнуться на вершину создаваемого остовного дерева и присоединить еще одну, а потом снова случайно выбрать точку в лабиринте и гулять, пока не попадем в одну из соединенных.
Олдос-Бродер избавлен от какого-либо смещения. Совершенно. Все лабиринты, получаемые с его помощью, абсолютно случайны и не похожи друг на друга. Алгоритм не имеет предпочтений по направленности, запутанности или ещё каким-либо характеристикам. Результирующие лабиринты случайны и равновероятны.
Проблемой может стать несовершенство генераторов случайных чисел, которые сами могут тяготеть к каким-либо значениям и выдавать их чаще. Но если использовать, к примеру, генератор случайности на основе природного шума (ветра, распада урана), то, пожалуй, вы сможете, наконец, в полной мере насладиться работой алгоритма.
Надо признать, наблюдение за его работой поистине даёт осознание всей тленности и бессмысленности бытия. Чтобы записать гифку с его анимацией, я потратил очень немало времени, так как укладываться в 30 секунд в поле 5×5 он упорно не хотел. Когда оставалось соединить всего одну последнюю непроверенную клетку к остовному дереву, Олдос-Бродер уходил в другой угол и наматывал там круги. Пришлось значительно увеличить скорость анимации и уменьшить поле, чтобы, наконец, он успел обойти все клетки лабиринта.
Его создали два независимых исследователя, изучавших равновероятные варианты остовных деревьев: Дэвид Олдос, профессор Калифорнийского университета Беркли и Андрей Бродер, учёный, ныне работающий в Google. Однозначно сказать, в какой сфере данные исследования были бы полезны, трудно. Однако, кроме лабиринтов, алгоритм часто всплывает в работах о математической вероятности, что, впрочем, неудивительно, учитывая принцип его работы.
Формальный алгоритм:
- Выбрать случайную вершину (клетку). Абсолютно случайную;
- Выбрать случайную соседнюю вершину (клетку) и перейти в неё. Если она не была посещена, добавить её в дерево (соединить с предыдущей, убрать между ними стену);
- Повторять шаг 2, пока все клетки не будут посещены.
Начинаем с левого верхнего угла. Тут ничего необычного.
Случайным образом решаем пойти направо и убрать стенку между двумя клетками. Хорошо, делаем.
Неповезло. Наш ГСЧ говорит, чтобы мы пошли обратно, то есть налево.
А теперь вниз. Попутно соединяем все непосещенные клетки и убираем между ними стены.
Еще раз повезло. Вниз!

Ладно, один возврат назад можно простить.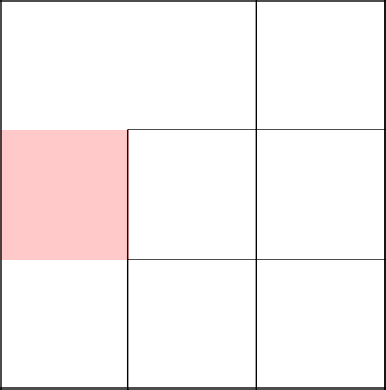
Выбираем пойти направо и убираем стену.
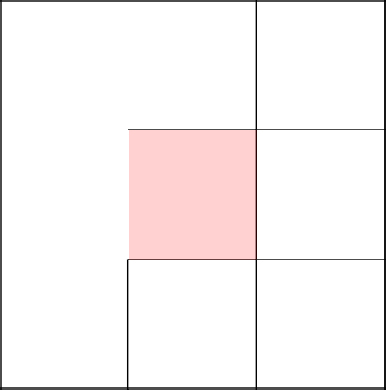
А тут нам дважды невезет и мы возвращаемся в самое начало.
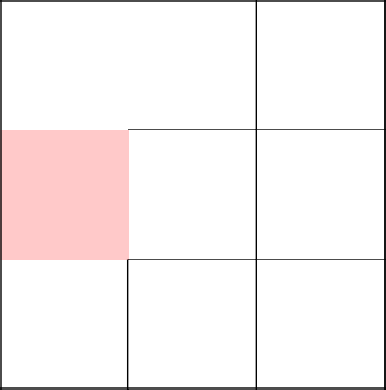

Выбор дважды пал пойти направо. Отлично, хоть какое-то разнообразие.
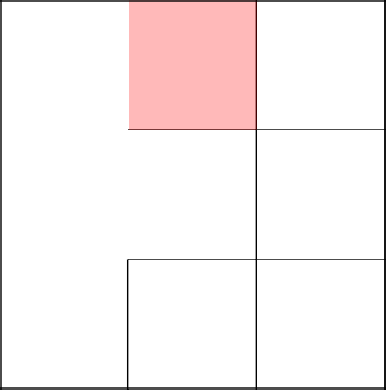

Спускаемся ниже и убираем стену.
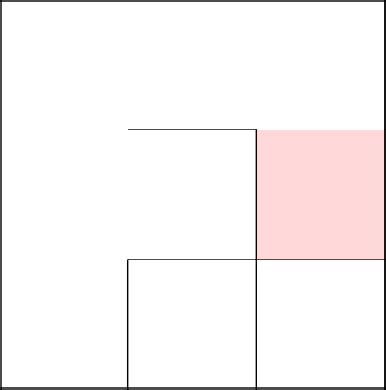
А вот тут мы хоть и перемещаемся в соседнюю клетку, стену не убираем, так как они уже в одном и том же дереве.
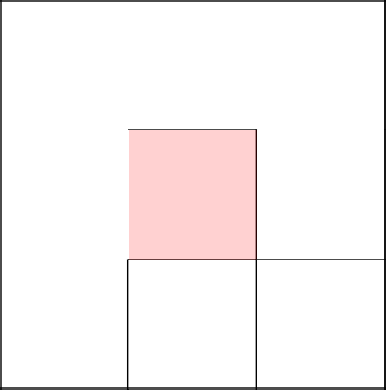
Пришло время бесцельно поблуждать, погулять.
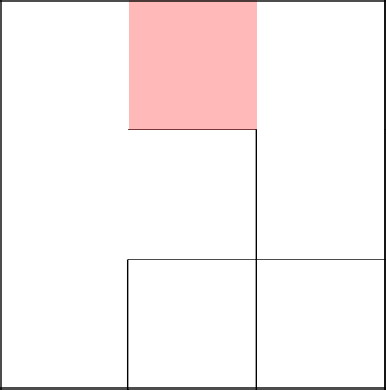



Возвращаемся к клетке 2–2 и спускамся ниже, убирая стенку.
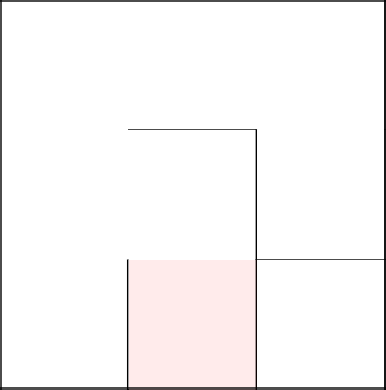
Завершаем нашу проголку и получаем сгенерированный лабиринт.

Плюсы:
- Отсутствует какое-либо смещение;
- Лабиринты абсолютно случайны, поэтому невозможно создать определенный алгоритм их решения;
- Сложность решения для человека;
- Простая реализация;
Минусы:
- Скорость. Пока будет генерироваться лабиринт, Вы успеете состариться и умереть;
- Не позволяет генерировать бесконечные лабиринты;
- Сильное падение эффективности под конец генерации;
local mod = {}
local aux = {}
aux.width = false
aux.height = false
aux.sx = false
aux.sy = false
aux.grid = false
aux.dirs = {"UP", "DOWN", "LEFT", "RIGHT"}
function aux.createGrid (rows, columns)
local MazeGrid = {}
for y = 1, rows do
MazeGrid[y] = {}
for x = 1, columns do
MazeGrid[y][x] = {visited = false, bottom_wall = true, right_wall = true}
end
end
return MazeGrid
end
function mod.createMaze(x1, y1, x2, y2, grid)
aux.width, aux.height, aux.sx, aux.sy = x2, y2, x1, y1
aux.grid = grid or aux.createGrid(y2, x2)
aux.aldous_broder()
return aux.grid
end
function aux.aldous_broder()
local unvisited_cells = aux.width * aux.height
local ix = math.random(aux.sx, aux.width)
local iy = math.random(aux.sy, aux.height)
aux.grid[iy][ix].visited = true
unvisited_cells = unvisited_cells - 1
while unvisited_cells ~= 0 do
local dir = aux.dirs[math.random(1, 4)]
if dir == "UP" then
if iy-1 >= aux.sy then
if aux.grid[iy-1][ix].visited == false then
aux.grid[iy-1][ix].bottom_wall = false
aux.grid[iy-1][ix].visited = true
unvisited_cells = unvisited_cells - 1
end
iy = iy-1
end
elseif dir == "DOWN" then
if iy+1 <= aux.height then
if aux.grid[iy+1][ix].visited == false then
aux.grid[iy][ix].bottom_wall = false
aux.grid[iy+1][ix].visited = true
unvisited_cells = unvisited_cells - 1
end
iy = iy+1
end
elseif dir == "RIGHT" then
if ix+1 <= aux.width then
if aux.grid[iy][ix+1].visited == false then
aux.grid[iy][ix].right_wall = false
aux.grid[iy][ix+1].visited = true
unvisited_cells = unvisited_cells - 1
end
ix = ix+1
end
elseif dir == "LEFT" then
if ix-1 >= aux.sx then
if aux.grid[iy][ix-1].visited == false then
aux.grid[iy][ix-1].right_wall = false
aux.grid[iy][ix-1].visited = true
unvisited_cells = unvisited_cells - 1
end
ix = ix-1
end
end
end
end
return mod
Алгоритм Уилсона



Описание
Поздравляю, мы, наконец, добрались до чего-то посерьезнее. Алгоритм Уилсона значительно сложнее всех предыдущих как в реализации, так и в понимании. Цель Уилсона, как и у своего более глупого напарник Олдоса-Бродера — генерация равновероятного случайного остовного дерева. И хотя принцип работы в чем-то схож, детали сильно различаются.
В основе алгоритма по-прежнему лежит равновероятный случайный выбор стороны перемещения в лабиринте (графе), с двумя важными отличиями:
Перемещаясь по полю мы «запоминаем» все вершины, в которых побывали до момента нахождения вершины остовного дерева. Как только мы натыкаемся на уже добавленную вершину, мы присоединяем получившийся подграф (ветвь) к нашему генерируемому дереву. Если создается цикл в подграфе, то удаляем его. Под циклом я подразумеваю соединение какой-либо вершины, которая уже находится во временном подграф с ним же, но в другой точке. Иначе говоря, не должно быть вершин, у которых больше 2 ребер. Если не понимаете сейчас, не страшно — дальше на примере работы наглядно увидите.
После присоединения подграфа к остовному дереву, выбор следующей случайной точки происходит исключительно из еще не присоединенных вершин. Следовательно, в отличии от Олдоса-Бродера, Уилсон лишен недостатка бесцельного блуждания по уже обработанным вершинам.
Алгоритм Уилсона, как и Олдос-Бродер, генерирует абсолютно случайные лабиринты без какого-либо смещения. Алгоритм не имеет предпочтений по направленности, запутанности или ещё каким-либо характеристикам. К сожалению, для получения наилучших результатов следует использовать аппаратные генераторы случайных чисел, которые не имеют предпочтений в числах.
Сам алгоритм был опубликован Дэвидом Уилсоном в 1996 году в своей работе о генерации равновероятных случайных остовных деревьев. Как и прежде, кроме лабиринтов, материалы всплывают на различных сайтах посвященных математической вероятностям. Более того, мне довелось наткнуться на несколько интересных публикаций, касательно Uniform Spanning Tree и алгоритма Уилсона в частности. Если в одной их них описывается больше сам алгоритм, то в другой в целом само понятие и математическая основа остовных деревьев.
Если читателям будет интересно, возможно, я напишу часть 2a, где приведу сами работы и их частичный перевод. Основная причина, почему я избегаю математического обоснования здесь — мои статьи направлены на новичков и людей, которым программирование интереснее сухой математики.
Формальный алгоритм:
- Выбрать случайную вершину, не принадлежащую остовному дереву и добавить её в дерево;
- Выбрать случайную вершину, не принадлежащую остовному дереву и начать обход графа (лабиринта), пока не придём в уже добавленную вершину дерева; Если образуется цикл, удалить его;
- Добавить все вершины получившегося подграфа в остовное дерево;
- Повторять шаги 2–3, пока все вершины не будут добавлены в остовное дерево.
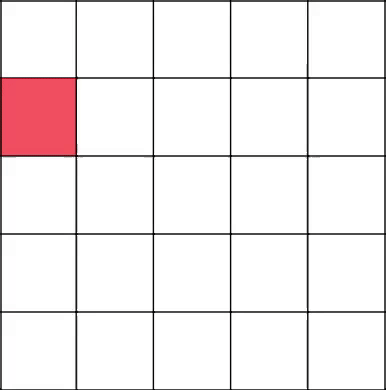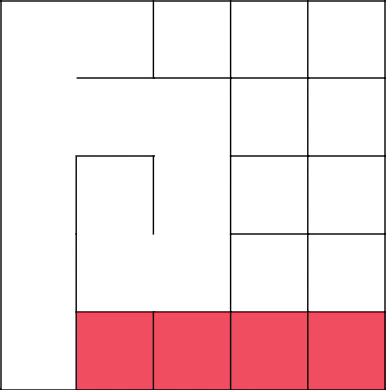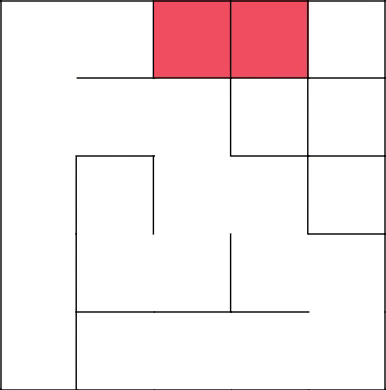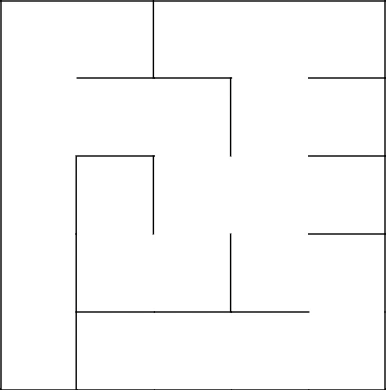
Традиционно, нужно попасть в левый верхний угол. Начинаем строить ветвь с координаты 3–2.
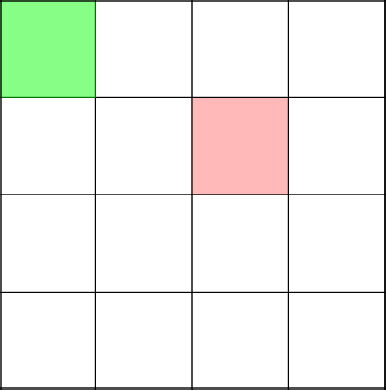

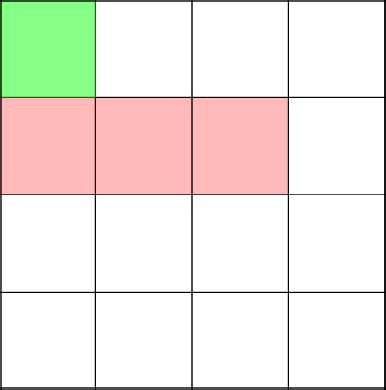

Вот сейчас интересный и важный момент. Алгоритм решает пойти наверх, тем самым замкнув ветвь в координате 2–2.
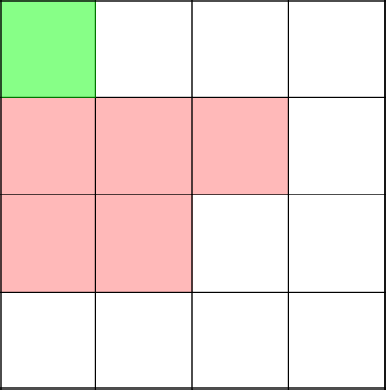
Удаляем получившийся цикл и начинаем с 2–2 строить заново.

habrastorage.org/files/e9c/8e6/46a/e9c8e646af564a42bbb391fbe263044b.png
Отлично, алгоритм решил пойти наверх и тем самым присоединился к основному дереву. Убираем стены на пути и выбираем следующую клетку.
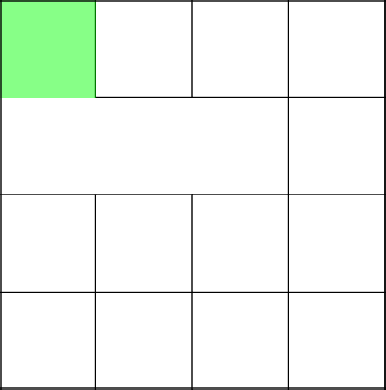
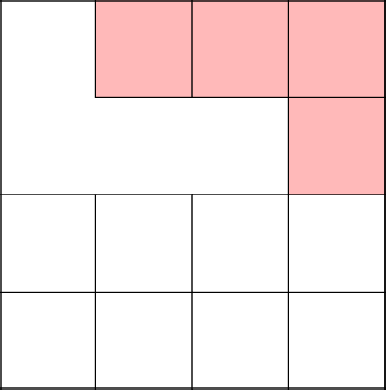
Вновь, коснулись созданного недавно дерева, убрали стены и начали заново.

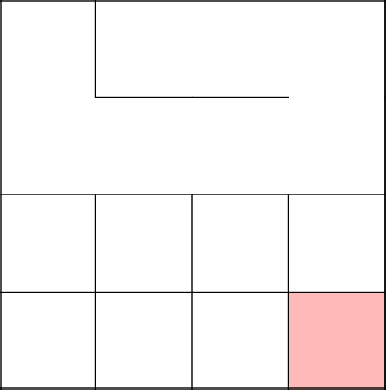
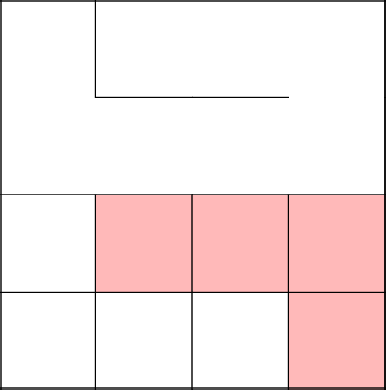
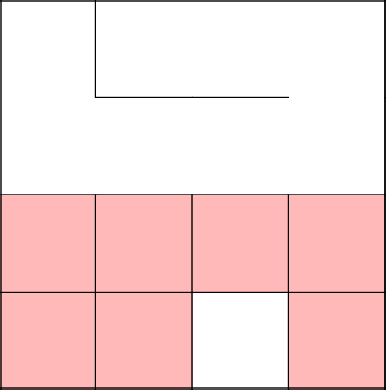
Замкнулись, убрали цикл, продолжили с 2–3 заново.

Соединились с деревом, очистили от стен путь. Продолжили наше путешествие в новой клетке.

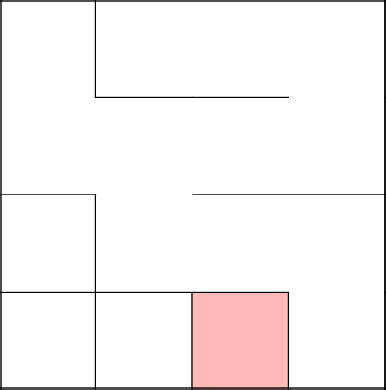
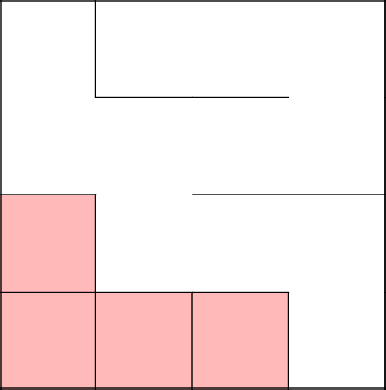
Снова соединились с основным деревом, убрали стены, закончили лабиринт.
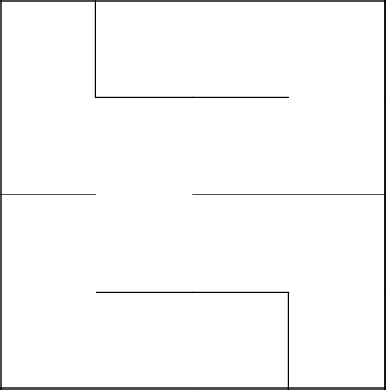
Плюсы:
- Отсутствует какое-либо смещение;
- Лабиринты абсолютно случайны, поэтому невозможно создать определенный алгоритм их решения;
- Сложность решения для человека;
- Нет бессмысленного блуждания;
- Скорость по сравнению с Олдос-Бродером в разы больше;
Минусы:
- Непростая реализация;
- Падения скорости в начале генерации;
- Большие требования к памяти, чем у Олдос-Бродера;
local mod = {}
local aux = {}
aux.width = false
aux.height = false
aux.sx = false
aux.sy = false
aux.grid = false
aux.dirs = {"UP", "DOWN", "LEFT", "RIGHT"}
function aux.createGrid (rows, columns)
local MazeGrid = {}
for y = 1, rows do
MazeGrid[y] = {}
for x = 1, columns do
MazeGrid[y][x] = {visited = false, bottom_wall = true, right_wall = true}
end
end
return MazeGrid
end
local function saveGridState()
local temp = {}
for yk, yv in pairs(aux.grid) do
temp[yk] = {}
for xk, xv in pairs(yv) do
temp[yk][xk] = {bottom_wall = aux.grid[yk][xk].bottom_wall, right_wall = aux.grid[yk][xk].right_wall}
end
end
return temp
end
function mod.createMaze(x1, y1, x2, y2, grid)
aux.width, aux.height, aux.sx, aux.sy = x2, y2, x1, y1
aux.grid = grid or aux.createGrid(y2, x2)
aux.wilson()
return aux.grid
end
function aux.hashKey(x, y)
return x * aux.height + (y - 1)
end
function aux.deHashKey(value)
return math.floor(value/aux.height), value%aux.height + 1
end
function aux.hashCells(grid)
local vtable = {}
for yk, yv in pairs(grid) do
for xk, xv in pairs(yv) do
if xv.visited == false then
vtable[aux.hashKey(xk, yk)] = xv
end
end
end
return vtable
end
function aux.wilson()
local cellsHash = aux.hashCells(aux.grid) -- Вершины, не находящиеся в дереве
local dirsStack = {} -- Стак направлений
local dsHash = {}
local dsSize = 0
-- Создаем дерево
local key, v = next(cellsHash, nil)
v.visited = true
cellsHash[key] = nil
while next(cellsHash) do -- Пока есть необработанные вершины, работает
key = next(cellsHash, nil) -- Получаем ключ и по нему координаты клетки
local start_x, start_y = aux.deHashKey(key)
local ix, iy = start_x, start_y
while not aux.grid[iy][ix].visited do -- Ходим, пока не найдем относящуюся к дереву клетку
local dir = aux.dirs[math.random(1, 4)]
local isMoved = false
key = aux.hashKey(ix, iy)
if dir == "UP" and iy-1 >= aux.sy then iy = iy - 1 isMoved = true
elseif dir == "DOWN" and iy+1 <= aux.height then iy = iy + 1 isMoved = true
elseif dir == "LEFT" and ix-1 >= aux.sx then ix = ix - 1 isMoved = true
elseif dir == "RIGHT" and ix+1 <= aux.width then ix = ix + 1 isMoved = true end
if isMoved then -- Если мы можем двигаться, тогда проверяем на циклы
if dsHash[key] then -- Удаление циклов
dirsStack[dsHash[key]].dir = dir
for i = dsHash[key]+1, dsSize do
local x, y = aux.deHashKey(dirsStack[i].hashref)
dsHash[dirsStack[i].hashref] = nil
dirsStack[i] = nil
dsSize = dsSize - 1
end
else
local x, y = aux.deHashKey(key) -- Добавление в стак направлений
dsSize = dsSize + 1
dsHash[key] = dsSize
dirsStack[dsSize] = {dir = dir, hashref = key}
end
end
end
for i = 1, dsSize do -- Проквапывание пути
aux.grid[start_y][start_x].visited = true
cellsHash[aux.hashKey(start_x, start_y)] = nil
aux.grid[start_y][start_x].point = false
local dir = dirsStack[i].dir
if dir == "UP" then
aux.grid[start_y-1][start_x].bottom_wall = false
start_y = start_y - 1
elseif dir == "DOWN" then
aux.grid[start_y][start_x].bottom_wall = false
start_y = start_y + 1
elseif dir == "LEFT" then
aux.grid[start_y][start_x-1].right_wall = false
start_x = start_x - 1
elseif dir == "RIGHT" then
aux.grid[start_y][start_x].right_wall = false
start_x = start_x + 1
end
end
dsHash, dirsStack, dsSize = {}, {}, 0 -- Обнуление стака направлений
end
end
return mod
Эпилог:
Суммируя всё выше сказаное, стоит отметить, что хотя мы и добрались до более сложных алгоритмов и разобрались с некоторыми новыми (для кого-то) понятиями графов, главные трудности ещё впереди. Неочевидно запутанные алгоритмы Эллера, Краскала и Прима, основанные исключительно на работе с графами и деревьями, готовят нам непростые, пусть и интересные публикации. Однако, прежде чем приступать к их написанию, следует взглянуть на алгоритмы поиска с возвратом и нечто под названием «Поймать&Убить», чья работа по генерации лабиринта сильно отличается от всех остальных. Намёк на тему следующей статьи я дал.
Что ещё. В комментариях к предыдущей части, некоторые люди спрашивали или скидывали свои алгоритмы генерации, что было крайне занимательно и радостно. Если Вы когда-то реализовывали создание лабиринтов своим придуманным способом и можете его сейчас вспомнить — прошу, поделитесь. Может быть, с вашего разрешения, в какой-нибудь из статей я напишу и о нём. Вообще, я рад любым интересным историям и воспоминаниям по теме. Не важно, вспоминаете ли Вы то, как рисовали лабиринты в тетраде в школе или на компьютере в университете.
Ну, и как всегда. Пожелания, критика, замечания всегда приветствуются и если Вам нравится тема и хотите видеть следующую часть, напишите об этом в комментариях.
