Какая ты кривая, или математика вокруг нас
Слово «математика» у кого-то ассоциируется с вечной зубрёжкой и строгим учителем, другие же представляют себе некоторую абстракцию, существующую отдельно от нашего мира, но есть и те, кто видит проявления этой науки в нашей повседневной жизни.
Вот, например, известно ли Вам, что форма зубцов на шестернях в обычных часах имеет гораздо более сложную форму, чем трапеция, и называется она волшебным словом «эвольвента окружности»? Вероятно, вы впервые слышите об этом, хотя каждый знаком и с механическими часами, и с шестернями. Вопрос, почему была выбрана эта форма, мы отдельно рассмотрим позднее. Но почему так много людей уверено, что математика — это нечто скучное и утомительное? Связано это в первую очередь с тем, что в большинстве школ дают только «базу» — основные математические понятия — без привязки к реальной жизни. Полученный таким образом материал кажется сухим и скучным. «Ну и где же я могу в жизни встретить эти тригонометрические уравнения?» — удивляется такой человек. Но стоит взглянуть чуть внимательнее, и откроется удивительный, сверкающий мир, причём хватит даже знаний в рамках школьной программы!
Справедливости ради стоит сказать, что — да, сейчас применяются далеко не все математические открытия и методы, но они уже готовы к использованию и просто ждут своего часа.

Николай Иванович Лобачевский (1792–1856)
Об одном таком случае хотелось бы рассказать. Наш соотечественник, великий математик Николай Иванович Лобачевский, ректор Казанского университета в 1827–1846, живший в XIX веке, много лет усердно разрабатывал новую, неевклидову геометрию. Однако после публикации своих трудов в 1832 году он подвергся жестокой критике и непониманию со стороны авторитетного математического сообщества. В Санкт-Петербургском журнале «Сын отечества» даже появилась обидная заметка: «Для чего же писать, да ещё и печатать, такие нелепые фантазии?». А всё потому, что в своей статье Лобачевский поставил под сомнение вроде бы очевидное утверждение о том, что через точку плоскости можно провести только одну прямую, не пересекающую данную. Николай Иванович в своей модели заменил это утверждение на совершенно противоположное: «Через любую точку можно провести более одной прямой, не пересекающую данную».
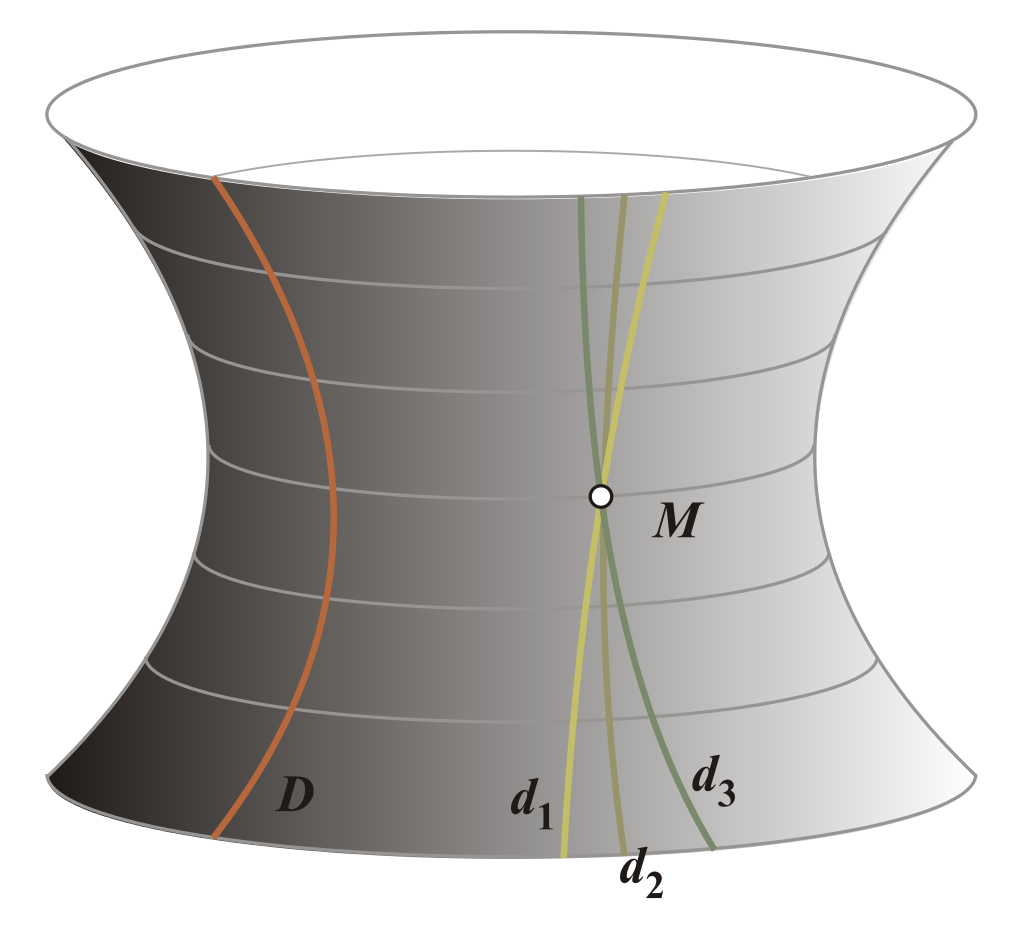
Визуализация геометрии Лобачевского: через точку М проходят 3 прямые, не пересекающие данную.
Даже после второй попытки публикации через 10 лет Лобачевский снова получает отрицательную оценку Михаила Остроградского — члена Санкт-Петербургской академии наук и признанного лидера математиков Российской империи в то время. Тогда Лобачевский решил познакомить со своими идеями иностранных учёных, и эта попытка оказалась вполне успешной. Сам «король математиков» Карл Фридрих Гаусс хорошо отозвался о новой геометрии, над которой и сам тогда работал, но на публикацию не решался также из-за опаски осуждения такой невероятной теории. Но нет пророка в своём Отечестве, и положение Лобачевского не улучшилось. Под конец жизни Николай Иванович и вовсе разорился, продал дом в Казани и имение жены. И лишь спустя 10 лет после смерти его прорывные взгляды были оценены мировым сообществом по достоинству, а труды учёного были переведены на все европейские языки. Что же мы имеем сейчас? Теория относительности утверждает, что даже в нашем реальном мире пространство не такое «ровное», как кажется, что для его описания используется модификация модели Лобачевского. Той самой модели, в которой сумма углов треугольника меньше 180 градусов, в которой плоскость можно замостить правильными десятиугольниками и т.д. Так, казалось бы, совершенно противоестественная и оторванная от реальности математическая теория нашла своё место! Но в своей статье я поведаю о более обыденных вещах — о том, где мы можем встретить разные математические кривые, вероятно, даже не подозревая об этом.
Степенные кривые
Простейшим примером кривой можно назвать, как ни странно, прямую. Что же вообще такое прямая? Вопрос не такой уж простой, ведь если попытаться на него ответить, в нашем ответе возникнут новые понятия, которые так или иначе будут использовать свойства привычной нам прямой. Но в математике всё строго, и, оказывается, что геометрического определения прямой просто не существует! Она вводится без определения. Но, думаю, любому читателю на уровне интуиции понятно, что же это такое. Прямую называют кривой первого порядка или кривой первой степени, то есть она задаётся уравнением первой степени в декартовых координатах, а именно ax + by + c = 0.
Но останавливаться на таком простом случае мы не будем. Наряду с такой «кривой» как «прямая» античные геометры выделяли как «совершенную кривую» окружность. Окружность — это кривая второго порядка, задающаяся всем известным уравнением: x2 + y2 = R2. Её определение уже может быть дано большим количеством способов, в частности, есть геометрическое определение: «Окружность — это множество всех точек плоскости, равноудалённых от данной точки». О важности окружности говорить не приходится — чего только стоит колесо. На этом математические кривые, изучаемые в школе, почти что заканчиваются, хотя есть ещё одна. Это — парабола, известная всем из алгебры как график квадратичной функции. Из такого определения, кстати, следует, что парабола — это кривая тоже второго порядка, как и окружность. Затем школьники сталкиваются с параболой на уроках физики, исследуя броски тела под углом к горизонту, а потом во время изучения вогнутых и выпуклых зеркал и линз. Там уже речь идёт о некоторых геометрических свойствах параболы. Но как вообще можно подходить к изучению геометрии параболы, если всё, что у нас есть — это какая-то там функция? Многим известно, что у параболы есть и классическое геометрическое определение. А именно: «Парабола — это множество всех точек плоскости, равноудалённых от данной прямой и данной точки». Эту точку называют фокусом параболы, а прямую — директрисой параболы.

Визуализация определения параболы с фокусом в точке F и директрисой a.
К примеру, если взять график функции y = x2, фокусом этой параболы будет выступать точка (0; 0.25), а директрисой — прямая y = -0.25. Таким образом, параболу, как и окружность, можно спокойно исследовать на геометрические свойства, которых, на самом деле, немало. Не вдаваясь в подробности, скажу, что совсем неочевиден тот факт, что алгебраическое и геометрическое определения дают одну и ту же геометрическую фигуру. Доказательство можно провести, воспользовавшись методом координат.
Теперь к главному — зачем нужна парабола? Да хотя бы для фонарика! И тем более она необходима в астрономии, при организации спутниковой связи, в военной и гражданской отрасли. Используется самое важное свойство параболы — оптическое, когда параллельный пучок света, отражаясь от параболы, собирается ровно в её фокусе, причём все лучи доходят до фокуса одновременно. Верно и обратное: если поместить источник света в фокусе параболы, то, отразившись от параболы, лучи будут представлять собой параллельный пучок света. Именно это поистине фантастическое свойство лежит в основе работы телескопов, спутниковых антенн и военных радаров. Давайте докажем это свойство.
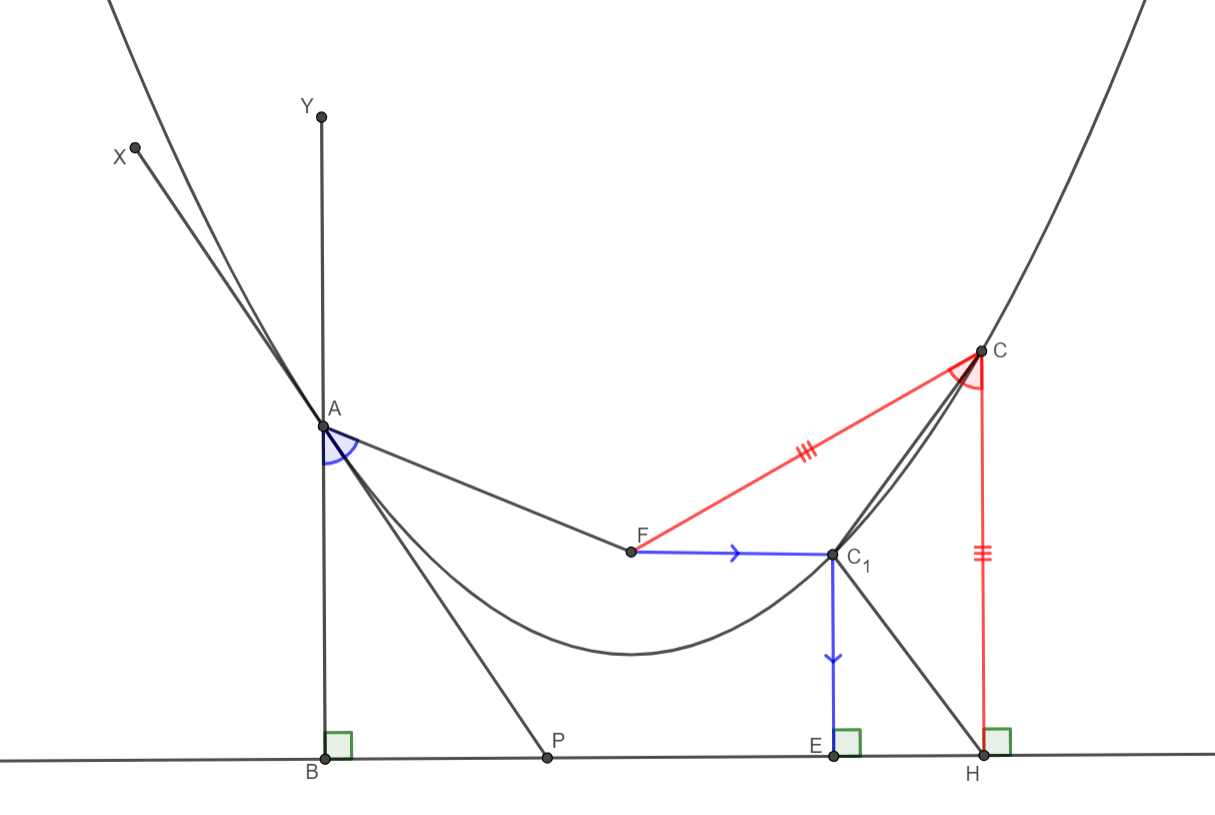
Отражением света от кривой можно считать отражением от касательной кривой в этой точке. Возьмём какую-нибудь точку А на параболе и проведём касательную XP через неё. Из физики известно, что угол падения равен углу отражения, поэтому наша цель — доказать, что угол BAP (который равен углу XAY) равен углу PAF, то есть касательная в точке A является биссектрисой угла BAF. Предположим, что это не так, тогда пусть есть точка C, и биссектриса угла FCH пересекает параболу в какой-нибудь точке C1. Тогда из определения параболы CF=CH, C1F=C1E. Но в то же время треугольники FCC1 HCC1 равны по 2 сторонам и углу, значит, FC1=HC1. Получилось, что в треугольнике EHC1 катет равен гипотенузе, но так не бывает. Значит, биссектриса угла FCH не пересекает параболу во второй раз, то есть касается её.
Интересен тот факт, что в учебниках физики при доказательстве свойств вогнутых и выпуклых зеркал многими несущественными отклонениями пренебрегают, в результате чего изучаемая поверхность имеет как свойства параболы, так и свойства окружности. Из этого можно сделать вывод о том, что, строго говоря, линз и зеркал, обладающих всеми этими свойствами, просто не бывает, их невозможно сделать. Однако на практике этим недостатком иногда действительно можно пренебречь.
Гипербола
Следующая кривая, которая затрагивается в школе — это гипербола — график функции y = k/x. Гипербола — также кривая второй степени, но где эта вторая степень? Она получается домножением обеих частей уравнения на икс:
xy = k — суммарная степень икса и игрека равна двум.
У гиперболы есть своё геометрическое определение: «множество всех точек
плоскости, модуль разности расстояний от которых до двух заданных точек,
называемых фокусами, постоянен».
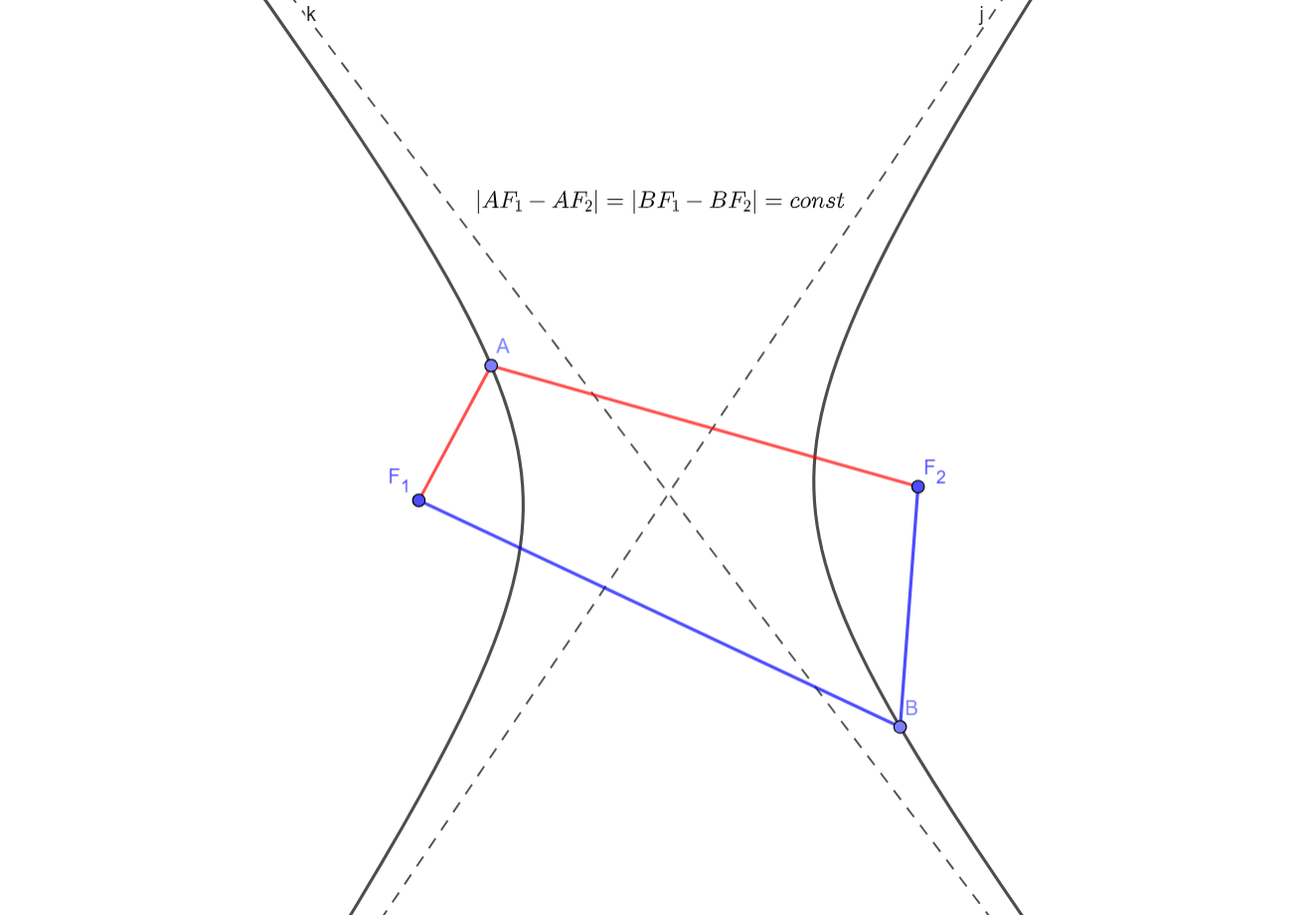
Понятное представление гиперболы с фокусами F1 и F2. Пунктиром проведены асимптоты.
Звучит страшновато, но суть этого определения можно понять из картинки. У любой гиперболы есть 2 асимптоты — прямые, к которым гипербола приближается, но никогда их не пересекает. Если брать гиперболу как график функции y = k/x, то её фокусы будут находиться в точках (√2; √2) и (-√2);- √2), а асимптотами будут оси координат. Но в общем случае для гиперболы асимптоты могут образовывать любой угол. Например, график функции y = x + 1/x — тоже гипербола с асимптотами x = 0 и y = x, угол между которыми равен 45⁰. Гипербола также обладает своим оптическим свойством, которое мы докажем несколько позднее, из-за чего она тоже используется в некоторых телескопах. Но чаще гиперболы, как, и параболы, встречаются в астрономии, ведь под воздействием гравитационных сил именно по гиперболе летят тела, имеющие достаточно высокую скорость. К примеру, гиперболическими траекториями обладают космические аппараты «Вояджер-1» и «Вояджер-2».
Эллипс
Последним примером кривой второго порядка является эллипс, известный как траектория движения планет вокруг солнца. Определять его можно большим количеством способов, даже как «растянутую окружность» в некотором смысле. Но в геометрии обычно используется следующее определение: «Множество всех точек, сумма расстояний от которых до двух заданных точек, называемых фокусами, постоянна». Очень похоже на определение гиперболы, только «разность» заменяется «суммой», что выглядит более естественно, благодаря чему эллипс можно даже нарисовать. Достаточно взять 2 гвоздика или 2 иголочки и зафиксировать их в фокусах предполагаемого эллипса, потом надеть на них ниточку, но так, чтобы она была не натянута, после чего взять карандаш, натянуть им ниточку и, не ослабляя натяжения, провести линию. Тогда этой линией будет эллипс.

Простой способ нарисовать эллипс
Конечно, в тетради таким способом эллипс не нарисовать, но это позволяет чуть лучше представить и прочувствовать эллипс. Конечно же, эллипс тоже обладает своим оптическим свойством. Если поместить источник света в фокусе эллипса, то после отражения от стенок эллипса все лучи сойдутся в другом фокусе, причём одновременно. Безусловно, роль света могут отыгрывать любые волны, например звуковые. Яркий пример использования этого свойства — метод литотрипсии в медицине, при котором возможно удалить камни из почек без хирургического вмешательства. Пациента располагают в эллиптической ванне так, чтобы почка с камнем находилась в одном из её фокусов. В другом фокусе ставят источник ультразвука. Отражаясь от стен, ультразвук собирается в одной точке и разрушает камень до состояния песка, который может выйти из организма естественным путём. Это невероятно полезное свойство эллипса тоже можно легко доказать, не выходя за рамки школьного курса, давайте сделаем это.
Для начала нам потребуется одна вспомогательная задача, известная как задача Герона. Если есть прямая АВ, а так же 2 точки P и Q с одной стороны от неё, то где на прямой AB поместить такую точку X, что сумма PX + QX минимальна? Давайте отразим точку Q относительно AB, получим точку Q'. Тогда искомая точка X находится на пересечении отрезка PQ и прямой AB. Действительно, возьмём любую другую точку Y на AB, тогда из неравенства треугольника PY + Q’Y > PQ' = PX + XQ, то есть для любой другой точки нужная сумма больше, чем для точки X. Из построения видно, что равны углы PXA и QXB. Это значит, что точка X такова, что свет, идущий из точки P, после отражения от AB в точке X, попадает в точку Q.

Решение задачи Герона
Вернёмся к эллипсу. Возьмём на нём какую-нибудь точку A и проведём через неё касательную XY. Мы хотим доказать равенство углов XAF1 и YAF2, то есть что точка A на прямой XY — это та самая точка из задачи Герона. Отметим другую точку на касательной к эллипсу и обозначим её за B. Поскольку эта точка лежит вне эллипса, то сумма BF1 и BF2 больше суммы AF1 и AF2 (это следует из определения эллипса). Значит, точка A на прямой XY такова, что сумма AF1 и AF2 минимальна, то есть это в точности точка из задачи Герона. А из этой задачи нам известно требуемое равенство углов.

Доказательство оптического свойства эллипса
Оптическое свойство гиперболы похоже на свойство эллипса и звучит оно так: «Если поместить точечный источник света в одном из фокусов гиперболы, то после отражения от ветви гиперболы лучи пойдут в таком направлении, что их продолжения пересекутся в другом фокусе». В терминах приведённой картинки нужно доказать равенство углов XAF1 и XAF2. Доказательство этого свойства аналогично случаю с эллипсом, только придётся немного изменить задачу Герона. Если интересно, можете попробовать провести рассуждения самостоятельно.
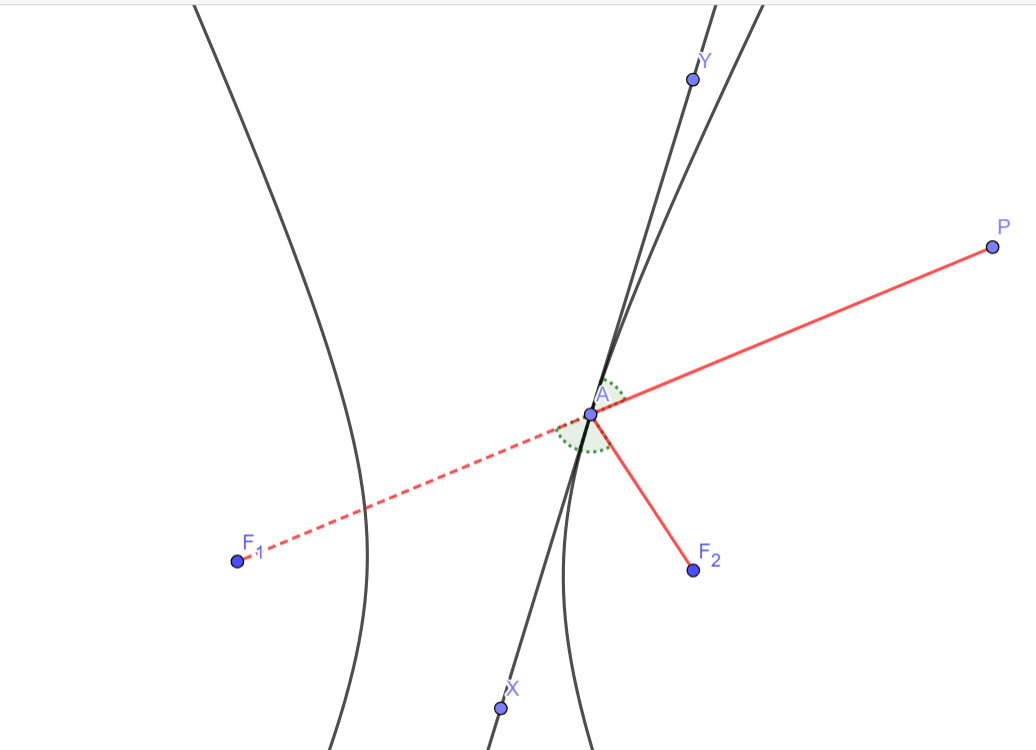
Оптическое свойство гиперболы
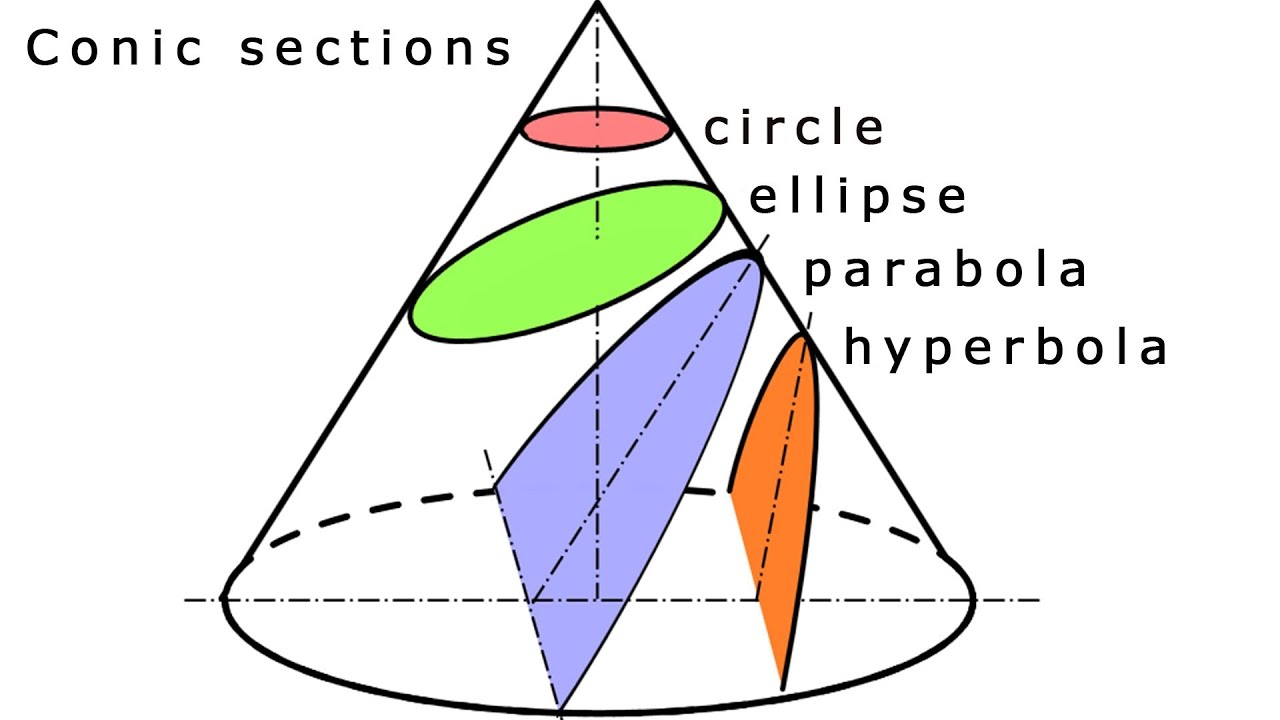
Вот мы и познакомились со каждой кривой второго порядка, но есть ли у них ещё что-нибудь общее? Оказывается, есть. Помимо большого количества общих геометрических свойств, любая из этих кривых может быть получена в сечении конуса (если быть точнее, то конической поверхности) плоскостью, поэтому их часто называют кониками.
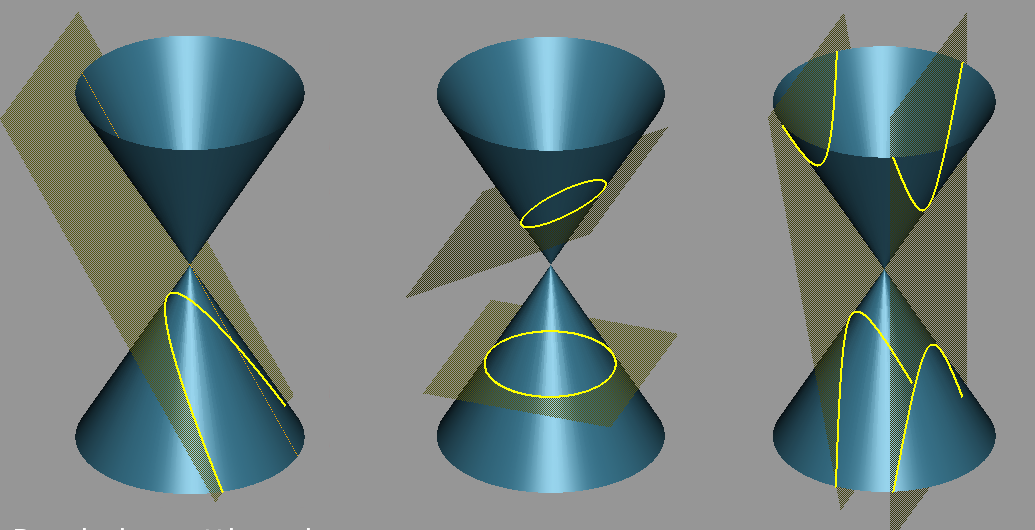
Если секущая плоскость параллельна одной из образующих конуса, то в сечении получается парабола (1-я картинка). Если плоскость пересекает все образующие только в одной «половинке», то получается эллипс (картинка 2). И, наконец, если плоскость пересекает обе «половинки» конуса, то сечение — гипербола, как на 3-й картинке. Окружность же считается эллипсом, у которого фокусы совпадают. Естественным образом коники встречаются и в геометрии, и в нашей жизни. К примеру, кончик стрелки солнечных часов в течение дня описывает гиперболу, движения космических тел часто происходят вдоль определенных коник.
Другие степенные кривые

Что касается коник, то на этом можно остановиться. Возможно, во время чтения статьи у читателя возник вопрос: «Раз есть кривые второй степени, то и более высоких степеней наверное тоже?» Да, кривые могут иметь какую угодно степень, но чем выше степень, тем больше возникает видов кривых и тем менее удобны они для изучения, так что о кривых степени выше четвёртой говорить особого смысла нет. После коник идут кривые третьей степени, или кубики. Простой пример кубики — кривая, являющаяся графиком уравнения y2 + y — 2xy2 = x3 — x2. Как видим, степень каждого слагаемого не превосходит 3.
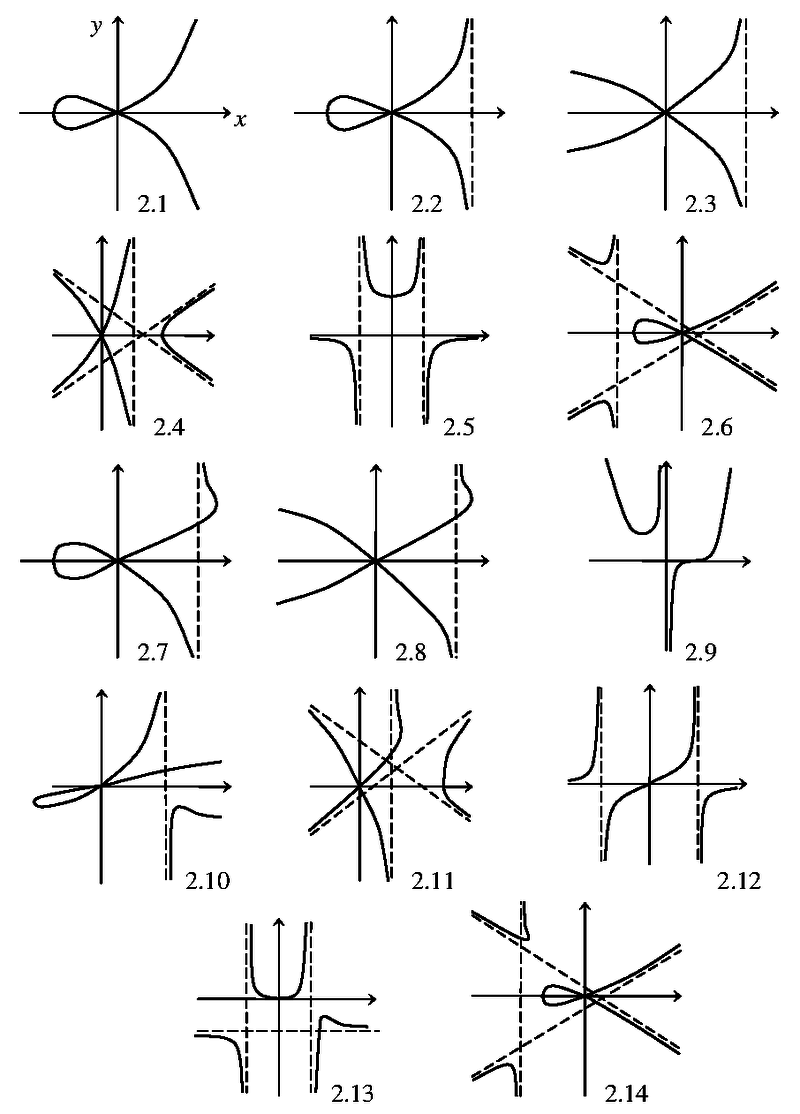
Некоторые виды кубик
Если существует всего 3 вида коник: эллипс, парабола, гипербола, то, поднявшись всего на одну степень вверх, мы получим уже более 50 разных видов кубических кривых! Кубические кривые, как и коники, часто естественным образом возникают в геометрии. Среди них, правда, особенно полезных немного. Особый вид кубических кривых, называемый эллиптическими кривыми, имеет большое значение в криптографии и шифровке данных, но все их свойства очень сложны, так что останавливаться на них я не буду.
Однако есть такая кривая, называемая кубической параболой — график уравнения y = x3. Эту кривую можно встретить на любой улице, ведь именно по кубической параболе часто делают дорожные повороты. Почему? Для ответа на этот вопрос придётся немного углубиться в понятие кривизны кривой. Чем больше кривизна, тем больше перегрузка, которая испытывается при повороте. И у кубической параболы кривизна меняется постепенно, что, хоть и не уменьшает перегрузку, но делает её плавной. На самом деле, кубическая парабола не является идеальной кривой для поворота, она лишь похожа на эту идеальную кривую, о которой мы поговорим несколько позднее, но используется она потому, что все расчёты, связанные с ней, значительно проще.
Сейчас речь пойдёт о способе использования кривых, о которых мы уже поговорили. Существует такое понятие, как сплайн. Если по-простому, то это несколько разных кривых, которые «состыковали» вместе. Часто используют кубические кривые, так как они могут иметь самые разные формы, и, соединив несколько их кусочков, можно получить практически что угодно. Это свойство сплайнов находит применение в компьютерной графике. Сплайнами иногда описываются некоторые физические процессы. Например, как будет выглядеть график зависимости температуры воды от количества приложенной теплоты? Сначала вода будет нагреваться пропорционально количеству тепла, графиком будет наклонённая прямая, затем, при достижении 100 градусов, температура перестанет расти, и вся теплота будет уходить на образование пара, графиком этого процесса уже будет горизонтальная прямая. И, наконец, когда вся вода испарится, пар станет снова нагреваться пропорционально приложенному теплу. График этого процесса — прямая, но имеющая другой угловой коэффициент, отличный от воды. Таким образом, график целого процесса — простейший сплайн, состоящий из 3 прямых. Если же изначально будет дан лёд с отрицательной температурой, то сплайн будет состоять уже из 5 частей.
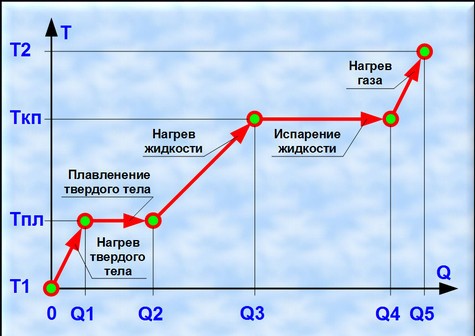
График процесса нагревания твёрдого тела
На этом со степенными кривыми, наконец, покончено. Перед тем, как мы поговорим о некоторых других кривых, хотелось бы немного уточнить понятие кривизны кривой. Вообще, оно тесно связано с понятием производной, но попробуем обойтись без него, пользуясь лишь интуицией. Сначала рассмотрим простой пример. Есть окружность, она вся симметрична, как ни посмотри. Поэтому и кривизна окружности одинакова во всех её точках. Если взять гиперболу, то ближе к центру она будет более «кривая», чем на некотором расстоянии, где она будет почти неотличима от прямой. Но как измерить кривизну кривой в произвольной точке? Достаточно определённым образом приблизить эту кривую окружностью в нашей точке, тогда кривизна кривой в этой точке будет равна кривизне такой окружности. У этой окружности есть хороший физический смысл. Из курса физики известно, что при равномерном движении по окружности тело имеет ускорение, направленное в центр этой окружности, при этом ускорение, скорость тела и радиус окружности связаны следующим соотношением: a * R = v2 или R = v2 / a. Так вот, та самая окружность, которая лучше всего приближает кривую, может быть получена, если подвигать тело вдоль кривой с постоянной скоростью и измерить его ускорение в нужной точке. И, воспользовавшись соотношением для центростремительного ускорения, найти радиус окружности. Этот радиус называют радиусом кривизны кривой в данной точке. А что касается кривизны окружности, то это есть величина, просто напросто обратная её радиусу. Например, у окружности с радиусом 2 см кривизна будет ½ = 0.5 см-1.

Окружности кривизны на примере гиперболы. Видно, что чем «кривее» наша кривая, тем меньше радиус её кривизны.
Мы вплотную подошли к рассмотрению идеальной кривой для дорожных поворотов. Такая кривая называется клотоидой или спиралью Корню. Она замечательна тем, что её кривизна изменяется равномерно. Это значит, что если дорога будет сделана по форме этой спирали, то, проезжая по ней, водитель будет поворачивать руль плавно, и это позволит входить в поворот почти без снижения скорости. Однако даже по виду этой кривой можно сказать, что она не может описываться каким-то примитивным уравнением. И поэтому на практике её обычно заменяют кубической параболой.
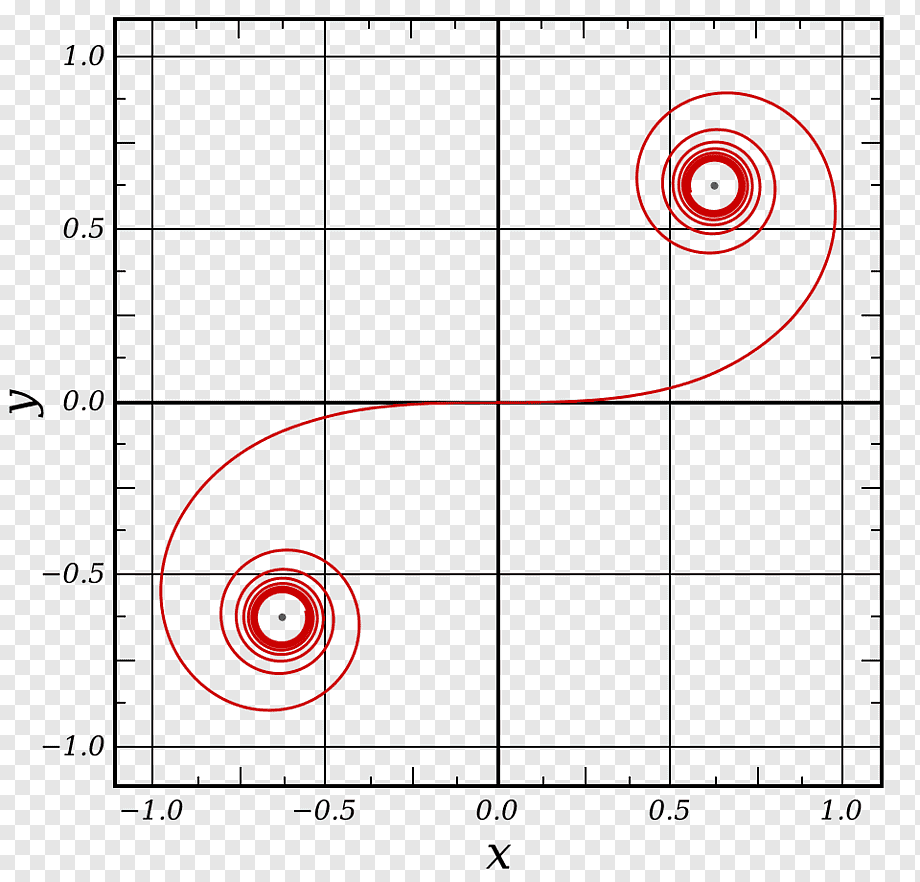
Клотоида
Эволюты и эвольвенты
Наверняка вы когда-нибудь задумывались, какую форму принимает, например, цепочка, подвешенная с двух концов, или верёвка, провисающая между двумя опорами? Эта кривая называется цепной линией. На первый взгляд эта кривая кажется похожей на параболу, но в действительности эта кривая задаётся совсем не интуитивным, хотя и несложным уравнением. А именно:
ch (x) — это функция так называемого гиперболического косинуса (иногда используется обозначение cosh (x)), где e~2.72 — число Эйлера. Какое отношение эта функция имеет к гиперболе, это отдельная и очень интересная тема, связанная с геометрией Лобачевского. В любом случае, совсем не ясно, откуда взялась эта формула. К сожалению, для её доказательства необходимо решить некоторое дифференциальное уравнение, пускай и не очень сложное, так что приводить доказательство я не буду. Но эту кривую можно использовать и в строительстве. Если её перевернуть, то полученная таким образом кривая будет иметь идеальную форму для конструкции моста, то есть если мост имеет такую форму, то нагрузка на поддерживающие его опоры будет минимальна. Если цепную линию вращать вокруг оси симметрии, то получится поверхность, являющаяся идеальной для строительства куполов.
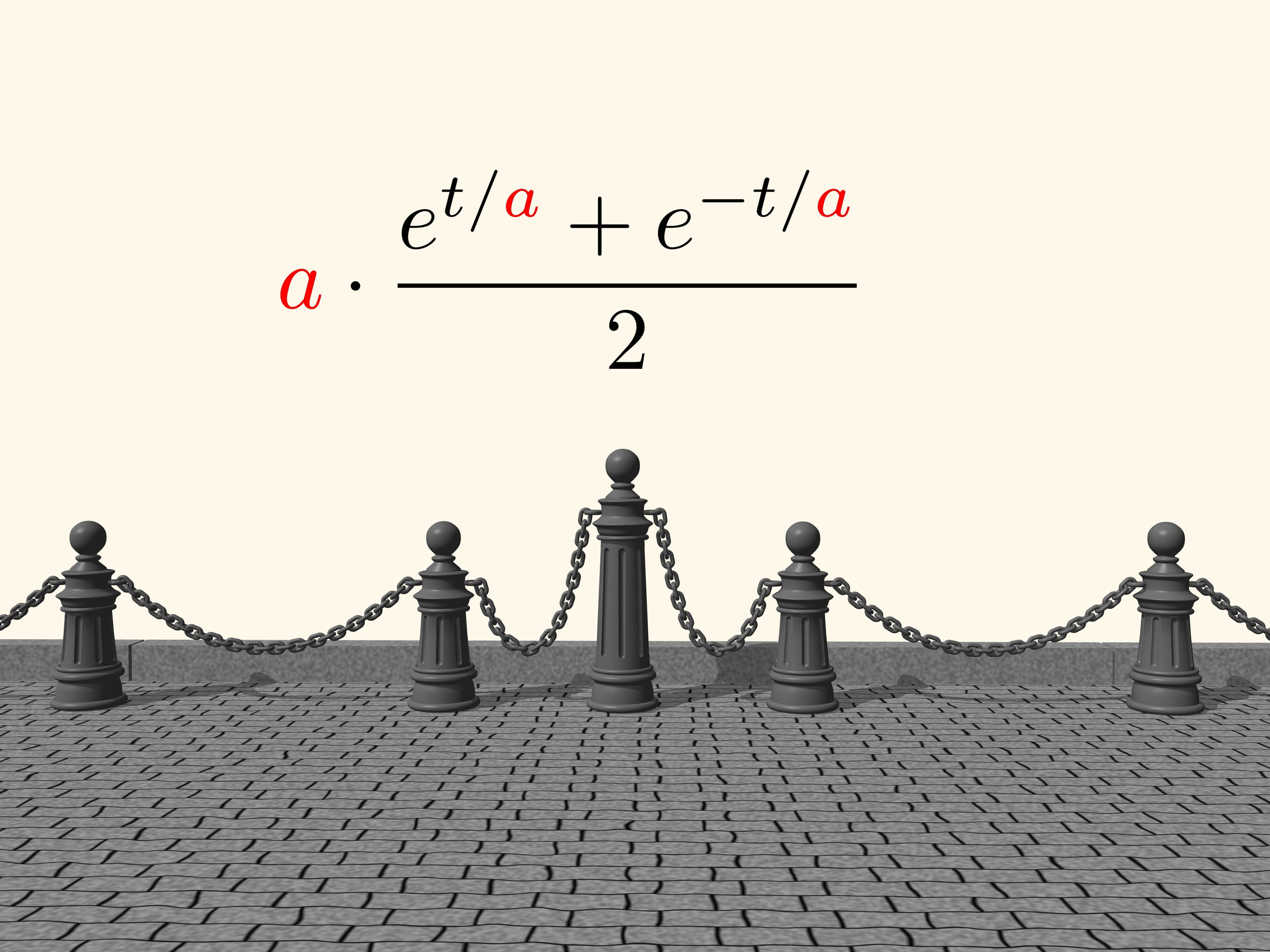
Но всё же с параболой у цепной линии немного больше общего, чем просто внешний вид. Цепную линию можно так же получить как траекторию движения фокуса параболы, катящейся по прямой без проскальзывания. Возможно читатель когда-то задавался вопросом: «Какую форму должна иметь дорога, чтобы по ней можно было ехать на квадратных колёсах без тряски?» Ответ — кочки на дороге должны иметь форму правильно подобранных цепных линий.
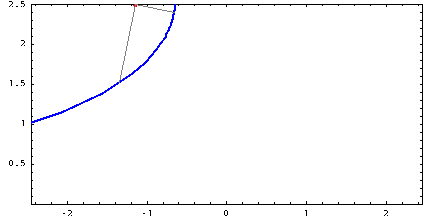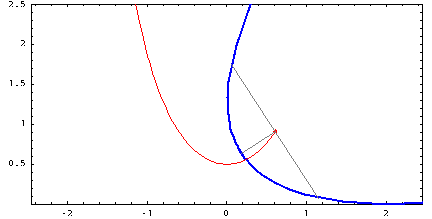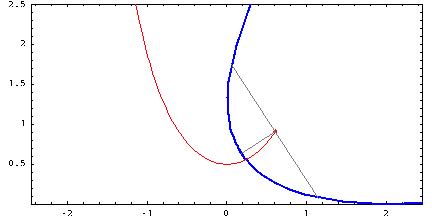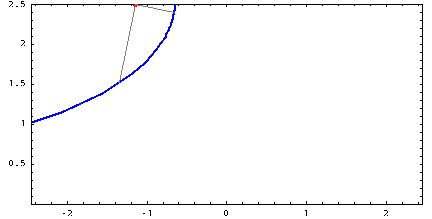
Синяя парабола катится по прямой, а её фокус движется по цепной линии.

Визуализация движения квадратных колёс по бугоркам в форме цепных линий.
С этой замечательной кривой тесно связана ещё одна. Пусть есть какой-то нерастяжимый стержень, лежащий на поверхности стола с достаточно большим трением. Будем медленно тянуть один конец стержня вдоль какой-нибудь прямой не по направлению стержня. Тогда какую траекторию будет описывать другой конец? Такая кривая называется трактрисой. Но есть у неё и другое, очень красивое название — эвольвента цепной линии. Кроме того, если вращать трактрису вокруг асимптоты, мы получим поверхность, называемую псевдосферой. Она замечательна тем, что имеет постоянную отрицательную кривизну, благодаря чему на ней можно реализовать уже не раз упомянутую геометрию Лобачевского.

Физическое построение трактрисы
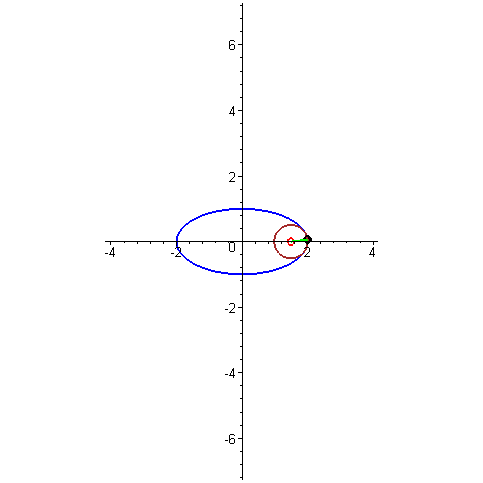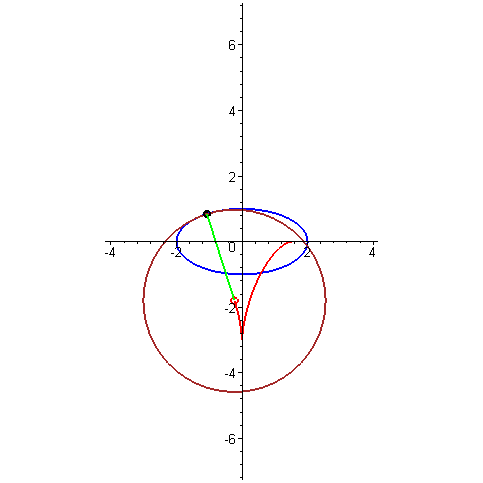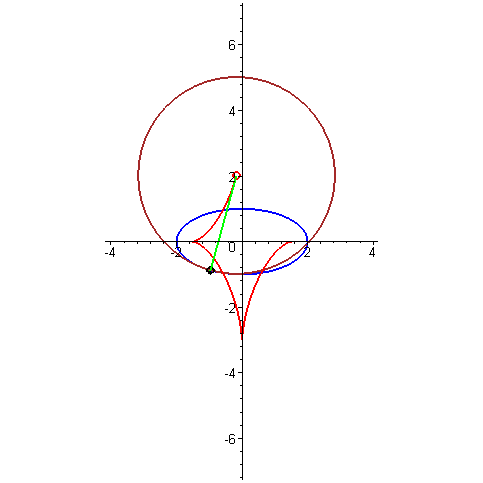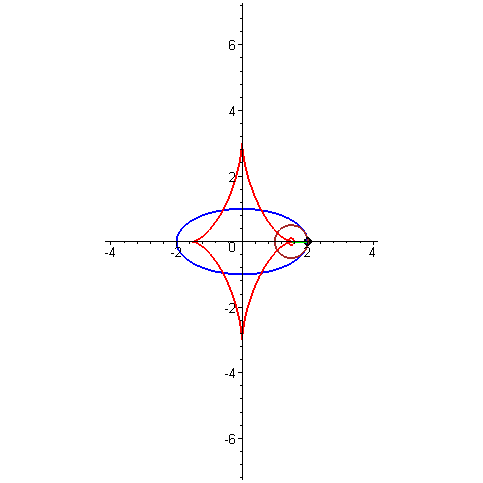
Построение эволюты на примере эллипса
На первый взгляд трактриса с цепной линией никак не связана, ведь их физический смысл совсем разный. Но между этими кривыми есть очень тонкая и красивая математическая связь. Если взять трактрису, отметить на ней какую-нибудь точку, провести через неё касательную к трактрисе, а затем провести перпендикуляр к касательной через эту же точку (этот перпендикуляр называется нормалью к кривой в данной точке), то он будет касаться некоторой цепной линии. Эту связь можно проиллюстрировать и по-другому: для каждой точки трактрисы проведём окружность кривизны (та самая окружность, которая наилучшим образом приближает кривую в этой точке), а затем отметим центры всех таких окружностей. Все эти центры образуют цепную линию. Если проделать такую же операцию, но с произвольной кривой, то получится другая кривая, называемая её эволютой. Таким образом, цепная линия — это эволюта трактрисы. Эвольвента — это то же самое, но в другую сторону. То есть если кривая A является эволютой кривой B, то кривая B является эвольвентой кривой A.
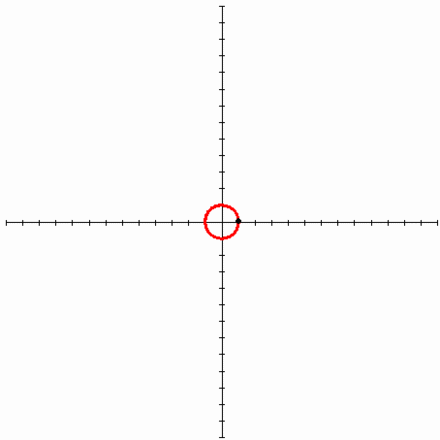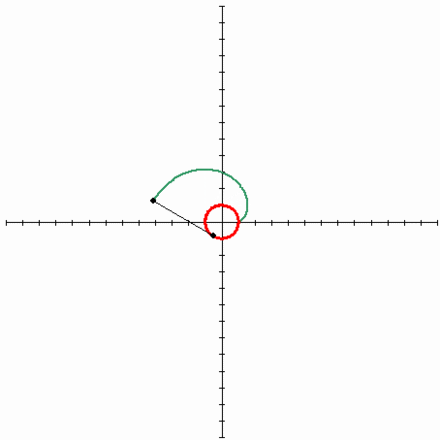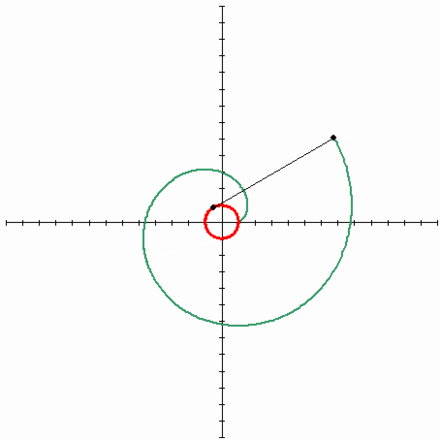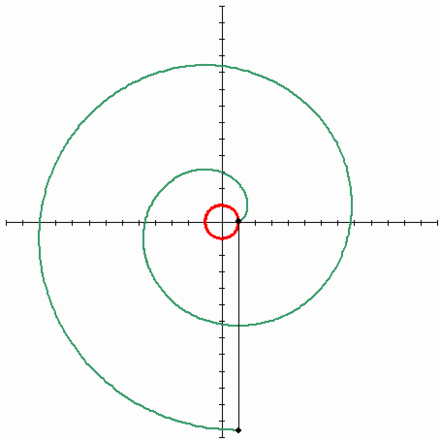
Эвольвента окружности
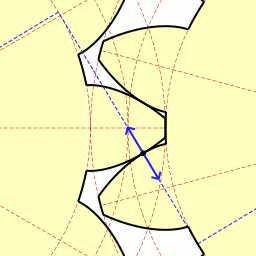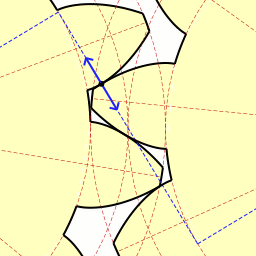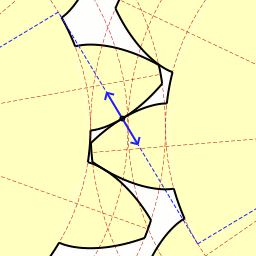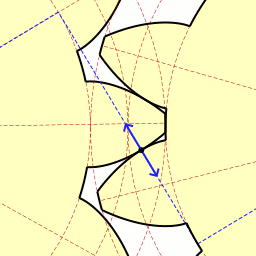
Зубья шестерёнок вырезаны по эвольвенте окружности, из-за чего шестерни всегда соприкасаются.
Наконец пришло время поговорить о такой замечательной кривой, как эвольвента окружности. Мне очень нравится эта кривая, она изящная и её легко построить. Достаточно зафиксировать в вертикальном положении катушку с нитками и начать разматывать нить, держа её натянутой. Тогда тот конец нити, что находится в руке, будет двигаться по эвольвенте окружности. Эта кривая имеет большое значение в зубчатом зацеплении, ведь если выточить зубья на шестернях по эвольвенте окружности и правильно соблюсти расстояние между соседними зубьями, то получится зубчатая передача, работающая без стука. Это означает, что контакт между шестернями всегда сохраняется, и поэтому обе шестерни могут двигаться равномерно. Именно это зацепление известно как эвольвентное.
Заключение
Конечно, существует ещё огромное количество кривых, которые так или иначе фигурируют в нашей жизни: логарифмическая спираль, синусоида, циклоида, лемниската, брахистохрона и т.д. Но о них мы поговорим как-нибудь в следующий раз.
Многие люди даже не подозревают, какой удивительный мир скрывается за порой обыденными вещами, и имя этому миру — математика. В своей статье я постарался познакомить читателя с этой параллельной вселенной, полной красоты и гармонии.
Надеюсь, вам понравилась моя первая статья, буду рад конструктивной критике)
