Как закалялась сталь современной симметричной криптографии. Глава 1. Классическая криптография
Введение
Современные симметричные шифры, которыми мы пользуемся неявно, но повсеместно, появились в ходе своей многовековой эволюции, в ходе продолжительных и постоянных этапов собственного совершенствования. Каждый новый шаг улучшения приводил одновременно к разрушению старых уязвимых шифров и к порождению новых, более качественных и безопасных. Тем не менее, само разрушение старых алгоритмов всегда двояко свидетельствовало как об их недостатках, которые необходимо было искоренять, так и об их достоинствах, которые нужно было наследовать. В следствие этого, каждый новый, более качественный шифр, представлял собой количественный синтез старых, менее качественных алгоритмов шифрования.
Таким образом, для того, чтобы узнать как современные симметричные алгоритмы шифрования стали такими, какими мы их сейчас видим, нам необходимо углубиться в историю шифров, а именно — в классическую криптографию. Основной нашей целью будет являться выявление примитивов шифрования на базе классических шифров и реструктуризация современных шифров по их композиции. Это даст понимание того, что современные симметричные шифры появились не просто из пустого места, а из структур ранее созданных алгоритмов шифрования.
Данный материал также может быть полезен коллегам преподавателям по предмету КСЗИ (криптографические средства защиты информации) и непосредственно самим студентам при изучении классической и современной симметричной криптографии. По ходу статьи будут прикладываться программные коды на языке Си некоторых шифров классической криптографии. В конце данной статьи также будет указан список литературы по классической и современной криптографии, с которым вы сможете ознакомиться.
Классическая криптография
Если начать с самого начала, с понимания того, как мы пришли к такой жизни, как люди научились создавать современные блочные/поточные шифры, нам необходимо углубиться в историю, а именно во времена, когда криптография ещё не являлась наукой, а была порождением искусства — в классическую криптографию.
Классическая криптография ныне является частью общей криптографии и представляет собой скорее исторический характер, нежели математический или информатический (современная криптография), относительно базисных наук. Таким образом, это говорит о том, что шифры которые будут описаны по ходу повествования, с большей долей вероятности не будут являться надёжными, и к ним нужно будет относиться исключительно как к экспонатам, играющим роль причины возникновения современных симметричных шифров.
Эпоху классической криптографии можно датировать периодом: 3000 л.д.н.э — первая половина XX в.н.э. Вторая половина XX века связывает себя с рождением криптографии как науки, где не малую роль сыграли следующие факторы: 1) Работа «Теория связи в секретных системах» (К. Шеннон), где были предложены базовые принципы шифров — конфузия и диффузия, было проведено математическое описание ранее существовавших шифров, доказано существование абсолютной криптостойкости на примере шифра Вернама; 2) Стандартизация шифра DES; 3) Появление нового раздела — асимметричной криптографии; 4) Информация о дешифровании Энигмы; 5) Появление криптографических хеш-функций; 6) Появление концепции ЭЦП; 7) Массовое применение в коммуникациях. Таким образом, всё что было в криптографии до второй половины XX века базировалось исключительно на необходимых мерах конфиденциальности передаваемой/хранимой информации, без признаков применения хеширования, ЭЦП, асимметричного распределения ключей и массового применения в коммуникации.
В классической криптографии, в явном виде, существовало два класса шифров — подстановочные и перестановочные. Суть первых сводится к тому, что один символ или группа символов открытого текста заменяется на один символ или группу символов закрытого текста. Суть вторых сводится к тому, что открытый текст «перемешивается» или «перетасовывается» таким образом, что он становится в конечном счёте закрытым. Вследствие этого, основным отличием перестановочных шифров от подстановочных является использование в закрытом тексте тех же символов открытого текста, в ровно таком же количестве и такой же пропорции. Это можно представить в виде следующей схемы.
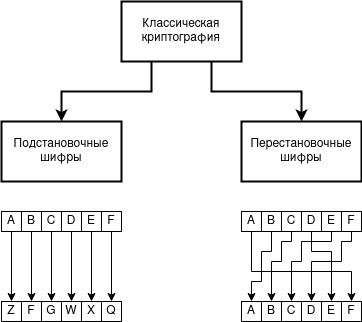
Классы шифров классической криптографии — подстановочные и перестановочные шифры
Подстановочные и перестановочные шифры также делятся на подклассы. Подстановочные шифры содержат пять подклассов, а именно: 1) коды, 2) моноалфавитные, 3) омофонические, 4) полиалфавитные, 5) полиграммные. Перестановочные содержат всего два подкласса: 1) простые и 2) сложные. Всю эту иерархию можно представить в виде следующей схемы.
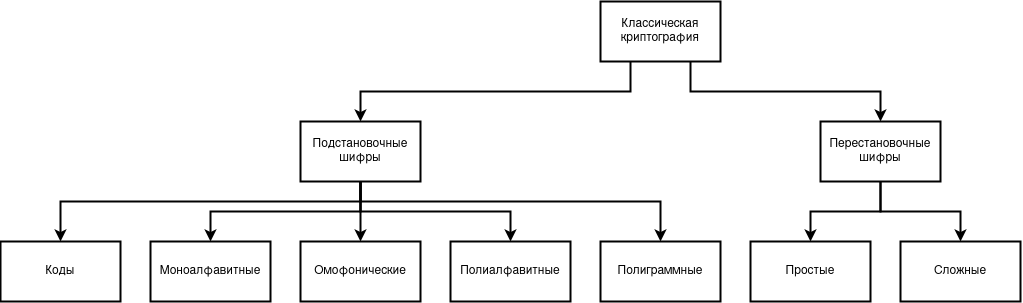
Классы и подклассы шифров классической криптографии
1. Коды
Являются самыми первыми методами шифрования в истории. Известно, что применялись в Древнем Египте, хоть и не в целях скрытия информации. Их суть заключается в замене (шифровании) целых слов на другие слова, группу символов или числа. Данный вид шифров можно видеть и в настоящем времени, где шпионы не говорят свои настоящие имена, а заменяют их псевдонимами. Ключевой особенностью кодов является существование кодовой книги по принципу «ключ-значение», например Алиса=Змея, Боб=Черепаха, Ева=Ящерица, а само сообщение может звучать так: «Змея-Змея, Ящерица вызывает Черепаху».
Коды могут также хорошо синтезироваться со стеганографией, то-есть не только шифровать сообщение, но и скрывать сам факт существования оригинального сообщения посредством другого (нейтрального) сообщения. Так например, сообщение «Я отнесу подарок часовщику в полдень» может трактоваться так: «Я положу бомбу у часовни в полночь». Если кодовая книга достаточно большая, то она может очень сильно искажать первоначальный смысл сообщения, «затмевая» истинное ложным. Хоть коды и представляют собой самый древний способ шифрования, тем не менее, при хорошо продуманной кодовой книге, результирующий шифр может оказаться сложно взламываемым даже в текущих реалиях.
При всём этом, стоит сказать, что коды не являлись основополагающими методами шифрования для развития классической криптографии, т.к. их основной проблемой являлась и продолжает являться прямая зависимость криптостойкости от размера кодовой книги. Для того времени это становилось (простите за мой каламбур) ключевой проблемой, потому как необходимо было иметь как минимум две копии одной и той же кодовой книги у двух людей на большой дистанции.
2. Моноалфавитные шифры
Являются отправной и ключевой точкой отчёта развития классической криптографии. Самыми старыми представителями подобного подкласса являются шифр Атбаш (~ 500 л.д.н.э.), шифр Полибия (~ III в.д.н.э.) и шифр Цезаря (~ I в.д.н.э.). В отличие от кодов, шифрующих целые слова, как элементарную единицу, моноалфавитные шифры нацелены исключительно на посимвольное шифрование. Также как и коды, моноалфавитные шифры имеют прямую связь между открытой элементарной единицей (слово/символ) и закрытой (слово/число/символ). Данную связь мы будем называть 1к1, где например, если открытый символ A преобразуется в закрытый символом B, то он не может ещё и преобразовываться в закрытый символ C, D, E и т.д. И наоборот, если закрытый символ B был получен из открытого символа A, то он не может быть расшифрован как-либо иначе кроме этого же символа A.
В качестве примера, часто приводят шифр Цезаря. Думаю вряд-ли кто-то с ним не знаком, если он хоть когда-нибудь начинал увлекаться криптографией. Основной особенностью шифра Цезаря является его ключ, представленный числом сдвигов оригинального алфавита. Так например, предположим, что у нас присутствует ключ K=1 и сообщение M=HELLO, тогда шифрованный результат будет выглядить как IFMMP. Если ключ K=3, то сообщение становится равным KHOOR. Итого, количество всех возможных ключей в шифре Цезаря выражается мощностью алфавита |A| (количеством символов). Если это английский алфавит, то существует всего |A|=26 ключей, если русский, то |A|=33 ключа и т.д. При этом всегда присутствует ключ равный нулю, в итоге количество «нормальных» ключей равно |A|-1.

Шифр Цезаря со сдвигом равным единице
Часто те кто начинает изучать классическую криптографию, испытывает путаницу в понимании различия между подстановочными и перестановочными шифрами. Иногда (хоть и редко) можно услышать, что шифр Цезаря — это перестановочный шифр. Путаница возникает на моменте вышепоказанной схемы, где действительно происходит обычная перестановка алфавита. Тем не менее, перестановочным шифром является алгоритм, при котором все символы исходного текста также находятся в шифрованном тексте, в ровно такой же пропорции — постоянно, как бы вы часто не меняли ключ шифрования. В контексте же шифра Цезаря, алфавит — это не открытый текст, а полученный алфавит после сдвига — не шифротекст. Можно сказать, более обще, что алфавит в шифре Цезаря — это есть часть ключа, посредством которой мы шифруем все последующие сообщения.
Тем не менее, если подойти к проблеме с другой точки зрения и представить алфавит как открытый текст, то тут уже действительно применяется перестановочный шифр, результатом которого становится ключ для шифра Цезаря. Но само применение перестановочного шифра при генерации ключа для другого шифра (будь то подстановочного или перестановочного) не свидетельствует о том, что другой шифр становится также перестановочным.
Программный код шифра Цезаря
#include "encoder.h"
#include
#include
#include
#include
typedef struct caesar_t {
encoder_t *encoder;
int32_t key;
} caesar_t;
extern caesar_t *caesar_new(encoder_t *encoder, int32_t k);
extern void caesar_free(caesar_t *caesar);
extern uint8_t *caesar_encrypt(caesar_t *caesar, uint8_t *output, uint8_t *input);
extern uint8_t *caesar_decrypt(caesar_t *caesar, uint8_t *output, uint8_t *input);
static uint8_t *encrypt_string(caesar_t *caesar, encmode_t m, uint8_t *output, uint8_t *input);
static int32_t encrypt_code(encoder_t *encoder, int32_t c, int32_t k);
int main(int argc, char *argv[]) {
uint8_t alphabet[] = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
uint8_t size_alph = (uint8_t)strlen((char*)alphabet);
encoder_t *encoder = encoder_new(size_alph);
encoder_set_alphabet(encoder, alphabet);
uint8_t message[BUFSIZ];
uint32_t key = 3;
strcpy((char*)message, "HELLOWORLD");
caesar_t *caesar = caesar_new(encoder, key);
printf("%s\n", (char*)caesar_encrypt(caesar, message, message));
printf("%s\n", (char*)caesar_decrypt(caesar, message, message));
caesar_free(caesar);
encoder_free(encoder);
return 0;
}
extern caesar_t *caesar_new(encoder_t *encoder, int32_t k) {
caesar_t *caesar = (caesar_t*)malloc(sizeof(caesar_t));
caesar->encoder = encoder;
caesar->key = k;
return caesar;
}
extern void caesar_free(caesar_t *caesar) {
free(caesar);
}
extern uint8_t *caesar_encrypt(caesar_t *caesar, uint8_t *output, uint8_t *input) {
return encrypt_string(caesar, MODE_ENC, output, input);
}
extern uint8_t *caesar_decrypt(caesar_t *caesar, uint8_t *output, uint8_t *input) {
return encrypt_string(caesar, MODE_DEC, output, input);
}
static uint8_t *encrypt_string(caesar_t *caesar, encmode_t m, uint8_t *output, uint8_t *input) {
size_t input_len = strlen((char*)input);
int encoded_ch, encrypted, flag;
for (int i = 0; i < input_len; i++) {
encoded_ch = encoder_encode(caesar->encoder, input[i], &flag);
if (flag == 0) {
fprintf(stderr, "undefined char %c;\n", input[i]);
return NULL;
}
encrypted = encrypt_code(caesar->encoder, encoded_ch, m*caesar->key); // m = {-1, 1}
output[i] = encoder_decode(caesar->encoder, encrypted, &flag);
if (flag == 0) {
fprintf(stderr, "undefined code %c;\n", encrypted);
return NULL;
}
}
output[input_len] = '\0';
return output;
}
static int32_t encrypt_code(encoder_t *encoder, int32_t c, int32_t k) {
uint8_t size = encoder_get_size_alphabet(encoder);
return (c+k+size)%size;
}
Файл encoder.h
#ifndef _H_ENCODER
#define _H_ENCODER
#include
typedef enum encmode_t {
MODE_ENC = 1,
MODE_DEC = -1
} encmode_t;
typedef struct encoder_t encoder_t;
extern encoder_t *encoder_new(uint8_t size_alph);
extern void encoder_free(encoder_t *encoder);
extern uint8_t encoder_get_size_alphabet(encoder_t *encoder);
extern void encoder_set_alphabet(encoder_t *encoder, uint8_t *alphabet);
extern uint8_t encoder_encode(encoder_t *encoder, uint8_t ch, int *found);
extern uint8_t encoder_decode(encoder_t *encoder, uint8_t code, int *valid);
#endif
Файл encoder.c
#include "encoder.h"
#include
#include
typedef struct encoder_t {
uint8_t size_alph;
uint8_t *alphabet;
} encoder_t;
extern encoder_t *encoder_new(uint8_t size_alph) {
encoder_t *encoder = (encoder_t*)malloc(sizeof(encoder_t));
if (encoder == NULL) {
return NULL;
}
encoder->size_alph = size_alph;
encoder->alphabet = (uint8_t*)malloc(sizeof(uint8_t)*size_alph);
return encoder;
}
extern void encoder_free(encoder_t *encoder) {
free(encoder->alphabet);
free(encoder);
}
extern uint8_t encoder_get_size_alphabet(encoder_t *encoder) {
return encoder->size_alph;
}
extern void encoder_set_alphabet(encoder_t *encoder, uint8_t *alphabet) {
for (int i = 0; i < encoder->size_alph; ++i) {
encoder->alphabet[i] = alphabet[i];
}
}
extern uint8_t encoder_encode(encoder_t *encoder, uint8_t ch, int *found) {
for (int i = 0; i < encoder->size_alph; ++i) {
if (encoder->alphabet[i] == ch) {
*found = 1;
return i;
}
}
*found = 0;
return 0;
}
extern uint8_t encoder_decode(encoder_t *encoder, uint8_t code, int *valid) {
if (code >= encoder->size_alph) {
*valid = 0;
return 0;
}
*valid = 1;
return encoder->alphabet[code];
}
Компиляция
gcc -Wall -std=c99 main.c encoder.cЗапуск
./a.outРезультат исполнения
KHOORZRUOG
HELLOWORLDТеперь, хоть мы и рассмотрели шифр Цезаря в подробностях, он всё равно является лишь единичным случаем (реализацией) всех моноалфавитных шифров. Благо моноалфавитные шифры можно обобщить. Так например, наивысшая криптостойкость всех моноалфавитных шифров выражается в лице шифра простой подстановки. Можно также в равной степени сказать, что шифр простой подстановки — это и есть целый подкласс в лице моноалфавитных шифров, потому как посредством него могут быть выражены все другие моноалфавитные шифры, будь то шифр Атбаш, шифр Цезаря, шифр Полибия, шифр Бэкона, Аффинный шифр и т.д. Следовательно, если шифр простой подстановки будет обладать определённым рядом уязвимостей, то все они также будут наследоваться побочными шифрами.

Шифр простой подстановки
Ключом в шифре простой подстановки является сам алфавит, а точнее его подстановочная версия. Так например, предположим, что имеется подстановка, которая указана на схеме выше и открытое сообщение M=HELLO. Результатом шифрования станет зашифрованное сообщение C=ITSSG. В отличие от шифра Цезаря, здесь нет вообще никакой перестановки даже на уровне алфавита, потому как могут существовать символы в подстановочной алфавите, которых не существует в оригинальном, и наоборот. Так например, символа @ не существует в оригинальном алфавите, а символа B не существует в подстановочном алфавите.
Шифр простой подстановки поражает количеством всевозможных ключей, потому как таковое количество становится равным факториалу мощности алфавита |A|! . Для английского алфавита количество ключей равно |A|!=26!=403291461126605635584000000, для русского |A|!=33!=8683317618811886495518194401280000000. Если очень грубо выражать данное количество ключей через сложность вычисления в битовом представлении современных симметричных шифров, то получится, что для английского алфавита сложность составляет ~=288, а для русского ~=2122. Для сравнения с текущими реалиями, считается, что длина ключа в 120 бит является вычислительно надёжной к полному перебору подготовленным криптоаналитиком с огромными вычислительными ресурсами.
Но не нужно быть такими наивными. Вышеописанная сложность будет работать лишь при том условии, когда шифр является идеальным в том простом плане, что у него не существует более никаких других уязвимостей, кроме полного перебора. Тем не менее, шифр простой подстановки имеет ряд уязвимостей. Это можно даже доказать на априорных знаниях, где существуют другие методы шифрования, отличные от моноалфавитных. Если бы моноалфавитный шифр являлся бы надёжным, то другие шифры скорее всего бы даже не разрабатывались и не были бы так знамениты в своих применениях. Но всё же, для лучшего понимания уязвимостей, нужно исходить из апостериорных знаний.
У шифра простой подстановки существует два основных вектора нападения — частотный криптоанализ и атака по маске. Первый вектор базируется на том факте, что у каждого алфавита, т.к. он естественный, существует некая избыточность символов, приводящая к тому, что одни символы в тексте встречаются гораздо чаще чем другие. Под текстом нам лучше понимать совокупность всех открытых текстов на выбранном языке. На практике конечно достаточно знать лишь несколько текстов с большим объёмом символов, чтобы выстроить частоту встречаемости каждого отдельного символа приближенную к частотам суммы всех текстов на данном языке. Второй вектор также базируется на факте избыточности символов в открытом тексте, но уже не на уровне каждого отдельного символа, как это предполагает частотный криптоанализ, а на уровне целой группы символов. Под группой символов могут выступать часто повторяемые слова, часто употребляемые приставки, суффиксы, предлоги, окончания, и т.д.
В любом случае, лучше будет попрактиковаться на примере данных векторов нападения. Предположим, что у нас существует следующий шифротекст. Известно, что таковой закрытый текст был получен посредством моноалфавитного шифра. Значит это говорит о том, что сохраняется связь символов между открытым и закрытым текстами 1к1.
Закрытый текст (моноалфавитный шифр)
AFD RPKOA PX AFKU AFPEJFA DSRDVKHDOA NZU AP UFPN AFD HZOT ZYDOEDU
PX ZAAZQC ZJZKOUA Z UTUADH, ZOM FPN XDN PX AFDH KOYPIYD AFD QPHREADV-
KLDM RPVAKPO PX AFD RVPQDUU. ND QZO ZAAZQC AFD AZWEIZAKPO UPXANZVD, ZOM
ND QZO HPEOA Z MDOKZI-PX-UDVYKQD ZAAZQC WT HZCKOJ AFD ZEAPHZAKQ UTUADH
XZKI ZOM XPVQKOJ AFD DIDQAKPO BEMJDU AP XZII WZQC PO ZO PIMDV, HPVD KOUDQEVD,
RVPQDMEVD XPV ZQQPHRIKUFKOJ AFD UZHD AZUC. KO AFD DOM, DIDQAKPOU ZVD ZWPEA
AVEUA. KX AFD DIDQAKPO BEMJDU ZVD AVEUANPVAFT ZOM QPHRDADOA, AFD DIDQAKPO
NKII WD XZKV. KX AFD DIDQAKPO BEMJDU ZVD OPA AVEUANPVAFT, AFDVD ZVD UP HZOT
NZTU AP VKJ AFD DIDQAKPO AFZA KA KUO’A DYDO NPVAF NPVVTKOJ ZWPEA NFKQF
POD KU HPUA IKCDIT.
AFD KOADVODA ZMMU ODN ANKUAU AP AFKU ZIVDZMT AZOJIDM UCDKO, ZOM AFD
VKUCU KOQVDZUD UKJOKXKQZOAIT. ZII AFD PIM ZAAZQCU VDHZKO, ZOM AFDVD ZVD ZII
AFD ODN ZAAZQCU ZJZKOUA AFD YPAKOJ QPHREADVU, AFD ODANPVC, ZOM AFD
YPADVU’ QPHREADVU (NFKQF ZVD OPA AVEUADM KO ZOT NZT). ZOM MDOKZI-PX-
UDVYKQD ZAAZQCU AFZA MPO’A DSKUA ZJZKOUA QDOAVZIKLDM UTUADHU. DYDO NPVUD,
HPMDVO DIDQAKPOU FZYD OP JVZQDXEI NZT AP XZKI. AFD 2000 MDHPQVZAKQ RVK-
HZVT KO ZVKLPOZ ZIIPNDM KOADVODA YPAKOJ. KX AFDVD NZU Z RVPWIDH, PV DYDO
UEURKQKPO PX Z RVPWIDH, NFZA QPEIM ZVKLPOZ MP? VDWPPA AFD DIDQAKPO ZOM
AVT ZJZKO AFD XPIIPNKOJ NDDC? AFKU VDZUPO ZIPOD KU DOPEJF AP QPOYKOQD
ZOT RUDRFPIPJKUA AP DUQFDN KOADVODA YPAKOJ.В исторической действительности же люди понимали (хоть и не сразу), что всеразличные символы точки, двоиточия, запятые, пробелы, абзацы и т.д. могут сыграть плохую роль в скорейшем взломе (дешифровании) закрытого текста. Поэтому они исключались и сам шифртекст выглядил как сплошной набор закрытых символов. Тем не менее, для примера взлома вполне сгодится более легковесная и лёгкая версия.
1) Частотный криптоанализ
Первое, что нам необходимо сделать — это вычислить частоты каждого отдельного символа в шифртексте. Для этого мы можем написать небольшую программу на Си, которая самостоятельно будет вычислять все частоты символов в закрытом тексте.
Программный код вычисления частот встречаемости символов
#include
// Читаем только английские символы большого регистра
#define ALPHA_SIZE 26
int main(void) {
FILE *file = fopen("encrypted.txt", "r");
if (file == NULL) {
return 1;
}
int ch, sum;
int frequency[ALPHA_SIZE] = {0};
while ((ch = fgetc(file)) != EOF) {
if ('A' <= ch && ch <= 'Z') {
frequency[ch-'A']++;
++sum;
}
}
for (int i = 0; i < ALPHA_SIZE; ++i) {
printf("%c = %5.2f%%;\n", 'A'+i, ((double)frequency[i])/((double)sum)*100);
}
fclose(file);
return 0;
}
Данная программа работает исключительно с символами ASCII, то-есть с английским алфавитом. Поэтому, если шифртекст будет написан на русском языке, то данную программу нужно будет переписать под поддержку кириллицы.
Получаем на выходе такие частоты. Здесь стоит помнить, что т.к. наш текст не сказать что большой, то и частоты могут перекрывать друг друга. Поэтому, при таком типе криптоанализа, становится необходимо иметь достаточно обширный текст, чтобы исключить как можно больше неопределённостей.
A = 11.49%;
B = 0.28%;
C = 1.29%;
D = 12.50%;
E = 2.11%;
F = 4.50%;
G = 0.00%;
H = 2.21%;
I = 3.77%;
J = 2.02%;
K = 6.89%;
L = 0.37%;
M = 2.85%;
N = 2.57%;
O = 7.90%;
P = 7.90%;
Q = 3.95%;
R = 1.47%;
S = 0.18%;
T = 1.75%;
U = 5.79%;
V = 5.51%;
W = 0.83%;
X = 1.93%;
Y = 1.29%;
Z = 8.64%;Теперь, второе, что нам необходимо сделать — это сравнить полученные частоты с оригинальными частотами символов английского алфавита.

Из сравнения мы видим, что (с большей долей вероятности) символ открытого текста E либо равен символу A закрытого текста, либо символу D закрытого текста. Оставшийся символ закрытого текста (A или D) должен будет также принадлежать (с большей долей вероятности) одному из первых оставшихся символов оригинального алфавита, то-есть к T, A, O, N или I.
Делаем предположение, что символ E=D по большей частоте встречаемости. На самом деле мы также могли сделать предположение, что символ E=A), потому как расстояние частот между символами A и D невелико. Оставшийся символ A предполагаем следующему символу оригинального алфавита T, иными словами делаем предположение, что T=A. Теперь заменяем все символы A, D в шифротексте на E и T. Получаем следующий текст.
Первая итерация дешифрования моноалфавитного шифра
tFe RPKOt PX tFKU tFPEJFt eSReVKHeOt NZU tP UFPN tFe HZOT ZYeOEeU
PX ZttZQC ZJZKOUt Z UTUteH, ZOM FPN XeN PX tFeH KOYPIYe tFe QPHREteV-
KLeM RPVtKPO PX tFe RVPQeUU. Ne QZO ZttZQC tFe tZWEIZtKPO UPXtNZVe, ZOM
Ne QZO HPEOt Z MeOKZI-PX-UeVYKQe ZttZQC WT HZCKOJ tFe ZEtPHZtKQ UTUteH
XZKI ZOM XPVQKOJ tFe eIeQtKPO BEMJeU tP XZII WZQC PO ZO PIMeV, HPVe KOUeQEVe,
RVPQeMEVe XPV ZQQPHRIKUFKOJ tFe UZHe tZUC. KO tFe eOM, eIeQtKPOU ZVe ZWPEt
tVEUt. KX tFe eIeQtKPO BEMJeU ZVe tVEUtNPVtFT ZOM QPHReteOt, tFe eIeQtKPO
NKII We XZKV. KX tFe eIeQtKPO BEMJeU ZVe OPt tVEUtNPVtFT, tFeVe ZVe UP HZOT
NZTU tP VKJ tFe eIeQtKPO tFZt Kt KUO’t eYeO NPVtF NPVVTKOJ ZWPEt NFKQF
POe KU HPUt IKCeIT.
tFe KOteVOet ZMMU OeN tNKUtU tP tFKU ZIVeZMT tZOJIeM UCeKO, ZOM tFe
VKUCU KOQVeZUe UKJOKXKQZOtIT. ZII tFe PIM ZttZQCU VeHZKO, ZOM tFeVe ZVe ZII
tFe OeN ZttZQCU ZJZKOUt tFe YPtKOJ QPHREteVU, tFe OetNPVC, ZOM tFe
YPteVU’ QPHREteVU (NFKQF ZVe OPt tVEUteM KO ZOT NZT). ZOM MeOKZI-PX-
UeVYKQe ZttZQCU tFZt MPO’t eSKUt ZJZKOUt QeOtVZIKLeM UTUteHU. eYeO NPVUe,
HPMeVO eIeQtKPOU FZYe OP JVZQeXEI NZT tP XZKI. tFe 2000 MeHPQVZtKQ RVK-
HZVT KO ZVKLPOZ ZIIPNeM KOteVOet YPtKOJ. KX tFeVe NZU Z RVPWIeH, PV eYeO
UEURKQKPO PX Z RVPWIeH, NFZt QPEIM ZVKLPOZ MP? VeWPPt tFe eIeQtKPO ZOM
tVT ZJZKO tFe XPIIPNKOJ NeeC? tFKU VeZUPO ZIPOe KU eOPEJF tP QPOYKOQe
ZOT RUeRFPIPJKUt tP eUQFeN KOteVOet YPtKOJ.Третье, что мы делаем — это пытаемся найти в полученном тексте какие-либо похожие слова. Так например, очень часто попадается комбинация символов равная tFe. В английском алфавите, присутствует схожая комбинация и тоже часто встречаемая равная символам THE. Если наши первоначальные предположения на счёт символов T и E оказались верными, то скорее всего сопоставление H=F тоже окажется верным. Это можно проверить на примере косвенных сопоставлений. Так например, в тексте есть ещё комбинация tFeH которая может быть равна THEN или THEM, также слово tFeVe, которое может быть равно THERE или THESE, и tFZt может быть равно THAT. Таким образом, H=F скорее всего точно является верным, т.к. мы нашли достаточно много косвенных совпадений. Заменяем F на H, параллельно заменяем Z на A, и пытаемся поразмыслить теперь над H = N или M, а также V = R или S. Плюс к этому, в полученном тексте начинает вырисовываться слово attaQCU из которого мы можем предположить ATTACKS. Если это верно, то мы расскрываем дополнительные сразу три символа C, K, S, а также ставим однозначную связь V=R (потому как символ S нам стал известен).
Вторая итерация дешифрования моноалфавитного шифра
the RPKOt PX thKs thPEJht eSRerKHeOt Nas tP shPN the HaOT aYeOEes
PX attack aJaKOst a sTsteH, aOM hPN XeN PX theH KOYPIYe the cPHREter-
KLeM RPrtKPO PX the RrPcess. Ne caO attack the taWEIatKPO sPXtNare, aOM
Ne caO HPEOt a MeOKaI-PX-serYKce attack WT HakKOJ the aEtPHatKc sTsteH
XaKI aOM XPrcKOJ the eIectKPO BEMJes tP XaII Wack PO aO PIMer, HPre KOsecEre,
RrPceMEre XPr accPHRIKshKOJ the saHe task. KO the eOM, eIectKPOs are aWPEt
trEst. KX the eIectKPO BEMJes are trEstNPrthT aOM cPHReteOt, the eIectKPO
NKII We XaKr. KX the eIectKPO BEMJes are OPt trEstNPrthT, there are sP HaOT
NaTs tP rKJ the eIectKPO that Kt KsO’t eYeO NPrth NPrrTKOJ aWPEt NhKch
POe Ks HPst IKkeIT.
the KOterOet aMMs OeN tNKsts tP thKs aIreaMT taOJIeM skeKO, aOM the
rKsks KOcrease sKJOKXKcaOtIT. aII the PIM attacks reHaKO, aOM there are aII
the OeN attacks aJaKOst the YPtKOJ cPHREters, the OetNPrk, aOM the
YPters’ cPHREters (NhKch are OPt trEsteM KO aOT NaT). aOM MeOKaI-PX-
serYKce attacks that MPO’t eSKst aJaKOst ceOtraIKLeM sTsteHs. eYeO NPrse,
HPMerO eIectKPOs haYe OP JraceXEI NaT tP XaKI. the 2000 MeHPcratKc RrK-
HarT KO arKLPOa aIIPNeM KOterOet YPtKOJ. KX there Nas a RrPWIeH, Pr eYeO
sEsRKcKPO PX a RrPWIeH, Nhat cPEIM arKLPOa MP? reWPPt the eIectKPO aOM
trT aJaKO the XPIIPNKOJ Neek? thKs reasPO aIPOe Ks eOPEJh tP cPOYKOce
aOT RseRhPIPJKst tP escheN KOterOet YPtKOJ.Из полученного результата мы также начинаем видеть ещё новые слова, например rKsks может быть равно risks (это подкрепляется также thKs => this), Neek может быть равно week (это подкрепляется также Nhat => what и Nas => was), reasPO может быть равно reason (это подкрепляется также RrPcess => process и tP => to, и eYeO => even). Все полученные комбинации также пытаемся заменить. Если будет что-то неверно, может попытаться вернуться назад.
Получаем уже такой текст, где его большая часть читается даже без последующего анализа и сравнения. Мы открыли следующие символы: t, h, e, p, o, i, n, t, o, r, v, w, c, k, s. В сумме 15, что представляет уже большую часть символов английского алфавита, более 50%. Далее, можете продолжить дешифровывать текст самостоятельно.
the point oX this thoEJht eSperiHent was to show the HanT avenEes
oX attack aJainst a sTsteH, anM how Xew oX theH invoIve the coHpEter-
iLeM portion oX the process. we can attack the taWEIation soXtware, anM
we can HoEnt a MeniaI-oX-service attack WT HakinJ the aEtoHatic sTsteH
XaiI anM XorcinJ the eIection BEMJes to XaII Wack on an oIMer, Hore insecEre,
proceMEre Xor accoHpIishinJ the saHe task. in the enM, eIections are aWoEt
trEst. iX the eIection BEMJes are trEstworthT anM coHpetent, the eIection
wiII We Xair. iX the eIection BEMJes are not trEstworthT, there are so HanT
waTs to riJ the eIection that it isn’t even worth worrTinJ aWoEt which
one is Host IikeIT.
the internet aMMs new twists to this aIreaMT tanJIeM skein, anM the
risks increase siJniXicantIT. aII the oIM attacks reHain, anM there are aII
the new attacks aJainst the votinJ coHpEters, the network, anM the
voters’ coHpEters (which are not trEsteM in anT waT). anM MeniaI-oX-
service attacks that Mon’t eSist aJainst centraIiLeM sTsteHs. even worse,
HoMern eIections have no JraceXEI waT to XaiI. the 2000 MeHocratic pri-
HarT in ariLona aIIoweM internet votinJ. iX there was a proWIeH, or even
sEspicion oX a proWIeH, what coEIM ariLona Mo? reWoot the eIection anM
trT aJain the XoIIowinJ week? this reason aIone is enoEJh to convince
anT psephoIoJist to eschew internet votinJ.От куда взят текст?
Книга — Секреты и ложь (Б. Шнайер)
P.S. На данном моменте (или даже раньше) могло возникнуть сомнение, что этот текст я уже знал и поэтому так легко его дешифровывал. На самом деле так и было, примерно пол года назад, пока я не удалил все открытые тексты. На моём ПК (а точнее на сервере) остались лишь самостоятельные работы для студентов, но без оригинальных текстов. Так что можно сказать, что это дешифрование было спонтанным.
2) Атака по маске
Данный вид криптоаналитической атаки схож по своему методу на частотный криптоанализ, но лишь с тем отличием, что таковой смотрит не на частоты встречаемости каждого отдельного символа, а на частоты встречаемости целых слов в тексте, или на частоты появления приставок, суффиксов, предлогов, окончаний и т.д. Следовательно, он заменяет два первых этапа частотного криптоанализа на этап сравнивания групп символов. В некой степени данный вид атаки является более простым и быстрым, если вы знакомы с языком, на котором написан текст.
Предположим, что у нас также существует тот самый текст. Забудем о том, что мы его смогли успешно дешифровать.
Закрытый текст (моноалфавитный шифр)
AFD RPKOA PX AFKU AFPEJFA DSRDVKHDOA NZU AP UFPN AFD HZOT ZYDOEDU
PX ZAAZQC ZJZKOUA Z UTUADH, ZOM FPN XDN PX AFDH KOYPIYD AFD QPHREADV-
KLDM RPVAKPO PX AFD RVPQDUU. ND QZO ZAAZQC AFD AZWEIZAKPO UPXANZVD, ZOM
ND QZO HPEOA Z MDOKZI-PX-UDVYKQD ZAAZQC WT HZCKOJ AFD ZEAPHZAKQ UTUADH
XZKI ZOM XPVQKOJ AFD DIDQAKPO BEMJDU AP XZII WZQC PO ZO PIMDV, HPVD KOUDQEVD,
RVPQDMEVD XPV ZQQPHRIKUFKOJ AFD UZHD AZUC. KO AFD DOM, DIDQAKPOU ZVD ZWPEA
AVEUA. KX AFD DIDQAKPO BEMJDU ZVD AVEUANPVAFT ZOM QPHRDADOA, AFD DIDQAKPO
NKII WD XZKV. KX AFD DIDQAKPO BEMJDU ZVD OPA AVEUANPVAFT, AFDVD ZVD UP HZOT
NZTU AP VKJ AFD DIDQAKPO AFZA KA KUO’A DYDO NPVAF NPVVTKOJ ZWPEA NFKQF
POD KU HPUA IKCDIT.
AFD KOADVODA ZMMU ODN ANKUAU AP AFKU ZIVDZMT AZOJIDM UCDKO, ZOM AFD
VKUCU KOQVDZUD UKJOKXKQZOAIT. ZII AFD PIM ZAAZQCU VDHZKO, ZOM AFDVD ZVD ZII
AFD ODN ZAAZQCU ZJZKOUA AFD YPAKOJ QPHREADVU, AFD ODANPVC, ZOM AFD
YPADVU’ QPHREADVU (NFKQF ZVD OPA AVEUADM KO ZOT NZT). ZOM MDOKZI-PX-
UDVYKQD ZAAZQCU AFZA MPO’A DSKUA ZJZKOUA QDOAVZIKLDM UTUADHU. DYDO NPVUD,
HPMDVO DIDQAKPOU FZYD OP JVZQDXEI NZT AP XZKI. AFD 2000 MDHPQVZAKQ RVK-
HZVT KO ZVKLPOZ ZIIPNDM KOADVODA YPAKOJ. KX AFDVD NZU Z RVPWIDH, PV DYDO
UEURKQKPO PX Z RVPWIDH, NFZA QPEIM ZVKLPOZ MP? VDWPPA AFD DIDQAKPO ZOM
AVT ZJZKO AFD XPIIPNKOJ NDDC? AFKU VDZUPO ZIPOD KU DOPEJF AP QPOYKOQD
ZOT RUDRFPIPJKUA AP DUQFDN KOADVODA YPAKOJ.Первое, на что наше внимание теперь должно быть приковано, так это к структуре самого текста. Нам нужно найти наибольшее количество закономерностей. Так например, группа символов AFD очень часто встречается в начале предложений, что может быть равно группе символов THE английского алфавита. Если это так, то мы сразу сможем узнать три правильных символа. Далее, моё внимание приковывают предложения с вопросами, потому как в английском языке вопросительные предложения строятся немного по другому в сравнении с обычными, а также имеют вспомогательные слова. Предположим, что в этих предложениях могут существовать слова WHAT, WHY, WHERE, HOW и т.д. Под WHAT может подходить шифртекст NFZA, т.к. никакие четыре символа не совпадают и находятся в вопросительном предложении. Далее очень часто в тексте встречается одиночный символ Z, который может быть равен символу A в английском тексте, который также подкрепляет гипотезу о WHAT=NFZA.
После того, как мы открыли несколько слов, нам будет легче продолжиать взламывать шифртекст, но уже посимвольно, как ранее мы это делали в частотном криптоанализе. На данном этапе, нам известны уже следующие символы: t, h, e, a, w. Если взглянуть вновь на частотный криптоанализ, то нам для этого текста было достаточно всего двух открытых символов для взлома всего текста, а именно T и E. Так что с полученным результатом также вполне реально доломать весь оставшийся шифртекст.
Программный код шифра простой подстановки
#include "encoder.h"
#include
#include
#include
#include
typedef struct simple_substitution_t {
encoder_t *orig_encoder;
encoder_t *encr_encoder;
} simple_substitution_t;
extern simple_substitution_t *simple_substitution_new(encoder_t *orig_encoder, encoder_t *encr_encoder);
extern void simple_substitution_free(simple_substitution_t *simple_substitution);
extern uint8_t *simple_substitution_encrypt(simple_substitution_t *simple_substitution, uint8_t *output, uint8_t *input);
extern uint8_t *simple_substitution_decrypt(simple_substitution_t *simple_substitution, uint8_t *output, uint8_t *input);
static uint8_t *encrypt_string(simple_substitution_t *simple_substitution, encmode_t m, uint8_t *output, uint8_t *input);
int main(int argc, char *argv[]) {
uint8_t alphabet_orig[] = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
uint8_t size_alph_orig = (uint8_t)strlen((char*)alphabet_orig);
encoder_t *encoder_orig = encoder_new(size_alph_orig);
encoder_set_alphabet(encoder_orig, alphabet_orig);
uint8_t alphabet_encr[] = "QWERTYUIOPASDFGHJKLZXCVBNM";
uint8_t size_alph_encr = (uint8_t)strlen((char*)alphabet_encr);
encoder_t *encoder_encr = encoder_new(size_alph_encr);
encoder_set_alphabet(encoder_encr, alphabet_encr);
uint8_t message[BUFSIZ];
strcpy((char*)message, "HELLOWORLD");
simple_substitution_t *simple_substitution = simple_substitution_new(encoder_orig, encoder_encr);
printf("%s\n", (char*)simple_substitution_encrypt(simple_substitution, message, message));
printf("%s\n", (char*)simple_substitution_decrypt(simple_substitution, message, message));
simple_substitution_free(simple_substitution);
encoder_free(encoder_orig);
encoder_free(encoder_encr);
return 0;
}
extern simple_substitution_t *simple_substitution_new(encoder_t *orig_encoder, encoder_t *encr_encoder) {
simple_substitution_t *simple_substitution = (simple_substitution_t*)malloc(sizeof(simple_substitution_t));
simple_substitution->orig_encoder = orig_encoder;
simple_substitution->encr_encoder = encr_encoder;
return simple_substitution;
}
extern void simple_substitution_free(simple_substitution_t *simple_substitution) {
free(simple_substitution);
}
extern uint8_t *simple_substitution_encrypt(simple_substitution_t *simple_substitution, uint8_t *output, uint8_t *input) {
return encrypt_string(simple_substitution, MODE_ENC, output, input);
}
extern uint8_t *simple_substitution_decrypt(simple_substitution_t *simple_substitution, uint8_t *output, uint8_t *input) {
return encrypt_string(simple_substitution, MODE_DEC, output, input);
}
static uint8_t *encrypt_string(simple_substitution_t *simple_substitution, encmode_t m, uint8_t *output, uint8_t *input) {
encoder_t *encoder_read, *encoder_write;
size_t input_len = strlen((char*)input);
int encoded_ch, flag;
switch (m) {
case MODE_ENC:
encoder_read = simple_substitution->orig_encoder;
encoder_write = simple_substitution->encr_encoder;
break;
case MODE_DEC:
encoder_read = simple_substitution->encr_encoder;
encoder_write = simple_substitution->orig_encoder;
break;
}
for (int i = 0; i < input_len; i++) {
encoded_ch = encoder_encode(encoder_read, input[i], &flag);
if (flag == 0) {
fprintf(stderr, "undefined char %c;\n", input[i]);
return NULL;
}
output[i] = encoder_decode(encoder_write, encoded_ch, &flag);
if (flag == 0) {
fprintf(stderr, "undefined code %c;\n", encoded_ch);
return NULL;
}
}
output[input_len] = '\0';
return output;
}
Библиотека encoder, а также способ компиляции находятся во вложении с кодом шифра Цезаря.
Результат исполнения
ITSSGVGKSR
HELLOWORLDВ итоге, на заре окончания использования моноалфавитных шифров уже было всем известно, что таковой подкласс шифров ни в коем случае нельзя считать надёжным. Хоть у него и вправду может существовать огромное количество ключей, тем не менее, у него существует и ряд значительных уязвимостей, позволяющих взламывать закрытый текст за считанные минуты. Люди того времени уже понимали на чём зиждется данная уязвимость, а именно на связи 1к1. Если такую связь скрыть, размыть или исключить, то частотный криптоанализ и атака по маске будут уже не такими эффективными орудиями в руках криптоаналитиков.
3. Омофонические шифры
Представляют собой развитие моноалфавитного подкласса, позволяющего шифровать один и тот же символ несколькими способами, тем самым образуя новый тип связи 1кN. Иными словами, теперь становится возможным отождествлять символ A одновременно с несколькими символами, как например B, C и D. При шифровании символа A случайным образом выбирается символ из данного множества, что как следствие, может порождать закрытый текст вида BCDBD из открытого текста AAAAA. Тем не менее, остаётся и в омофоническом шифре «наследие» моноалфавитного, а именно расшифрование становится всегда однозначным относительно множества закрытых символов. Так например, если A способен преобразовываться в B, C или D, то B, C и D не могут расшифровываться никак иначе как символ A. Поэтому связь и является однонаправленной. Представителем подобных шифров является книжный шифр (не путать с книжным шифром из стеганографии).
Главной целью омофонических шифров является сокрытие частот встречаемости каждого отдельного символа посредством их выравнивания. Так предположим, что существует алфавит всего из трёх символов {A, B, C}. Предположим, что в текстах на этом языке, A=X (где X — шифросимвол) встречается в 50% случаев, а символы B=Y и C=Z в 25% случаев каждый. В моноалфавитном шифре частота символа X всегда бы сохранялась и была равна частоте символа A открытого текста, из-за чего могла бы применяться атака частотным криптоанализом. Омофонический же шифр размывает частотную закономерность посредством «деления» символа на несколько символов шифртекста. Так например, если A разделить на два символа Q и W, и при шифровании с равной и случайной вероятностью выбирать один из них, то символы Q и W, вместе с символами Y и Z будут иметь вероятность встречаемости по 25% каждый. Из этого следует, что применять на шифртекст с правильной омофонической заменой атаку частотного криптоанализа более становится невозможно.
Омофонический шифр, искореняя атаку частотным криптоанализом, вдобавок и повышает количество возможных ключей при полном переборе. На первый взгляд кажется, что вот он, идеальный шифр, у которого более не существует уязвимостей, а полный перебор просто неосуществим на практике. Но вы ведь ещё не забыли об атаке по маске? Хоть атака по маске и представляет собой некий частный случай атаки частотного криптоанализа, но за счёт того, что атака по маске анализирует закономерность на уровне групп символов, то и векторы нападения начинают немного отличаться. Эта атака становится губительной для омофонических шифров.
Основная суть атаки сводится к тому, что омофонический шифр (пока не берём в расчёт книжный шифр) име
