Как устроены волны12.04.2021 14:48

Волны — это самое распространённое явление. Физические колебания, звук, свет, радио и рентген, волны вероятности в квантовой механике, гравитационные волны в теории относительности — физика практически состоит из волн. Каждое явление можно изучать отдельно, но есть что-то общее в волнах, универсальное.

Чтобы ухватить это общее предлагаю разбираться в волнах последовательно.

Начнём с вопроса, на первый взгляд не связанного с темой, но ответ на который сразу много прояснит.

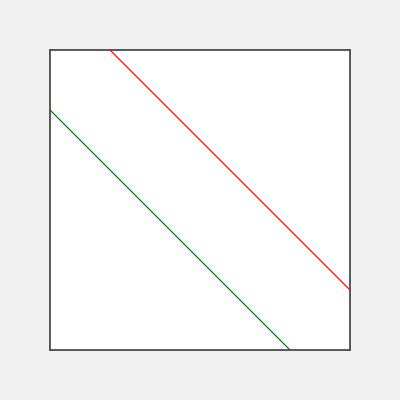Рис. 1. «Две параллельные линии». Канва, браш. Рама.
Перед вами две параллельные линии, с ограниченной областью их просмотра, квадратным окном. Для различия они раскрашены. Вопрос простой: если красная линия это сдвинутая зелёная, то в какую сторону произошел сдвиг?
Варианты:

1. По диагонали вправо-вверх.
2. Вправо.
3. Вверх.
4. Могут быть все три предыдущих ответа.
5. Не только отдельно вверх или вправо, но и все промежуточные направления…
6. Другой ответ, так как некоторые возможности не указаны.

Основы

Представляю вашему вниманию: волна, в самом естественном виде.

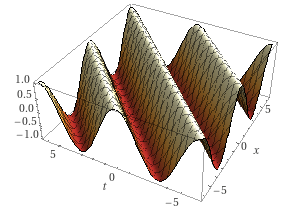
Рис. 2. Волна в движении. (Здесь задумана анимация. Но вместо анимации пространственного среза — функция от пространства и времени)
Что изображено? Пространственный профиль.
Какая особенность? Он движется, и при этом не меняется.
В самом общем смысле волна это соединение пространства и времени через распределённое, но единое содержание.
Разумеется, волна — это больше, чем движение профиля, но для демонстрации этого нужны дополнительные пояснения.

В предваряющей статье о разборе круга рассказывалось о том, как понятие производной дополняет определение круга, это не просто постоянство суммы квадратов координат.

Статья получилось длительной. Было интересно последовательно разобрать одну тему и посмотреть, что получится. Советую читать не торопясь, и только если интересно.

***

Как вам картина (Рис. 1)? Эти две линии напоминают два идущих друг за другом гребня волны. Но правильный ответ на вопрос о направлении сдвига, как ни странно, шестой — «И не только промежуточные». Потому что направление может быть любое, кроме направления вдоль самой линии. Если не допускать отрицательной величины сдвига, то можно, конечно, исключить направления, для которых нужно двигаться в обратную сторону. Но движение по таким направлениям, которые приближены к самой линии больше, чем направление вверх или вправо — тоже вариант.

Например, сдвиг, который складывается из двух шагов вверх и одного шага влево. Сумма коэффициентов при смешивании у шагов вправо и вверх единица, даже если один из коэффициентов отрицательный. Такое, допускающее внутренние варианты, равенство. А с применением комплексный чисел в сумме одно из слагаемых может быть отрицательным, даже если складываются квадраты.

Движение пространственного профиля во времени может быть представлено функцией от двух аргументов, от пространства и времени. Причём, у такой функции значения вдоль диагонали, совпадающей своим направлением с совмещением движения профиля в пространстве и времени, будет сохраняться. Производные такой функции вдоль координаты пространства и вдоль координаты времени будут по абсолютному значению равны, но противоположны по знаку.

Если бы профиль двигался в другом направлении, влево, то производная по пространству осталась бы той же, а производная по времени поменяла бы свой знак, и они стали бы равны.

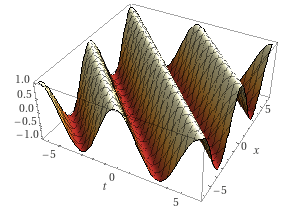По сравнению с предыдущим изображением здесь есть одно простое изменение.
Вторые производные по пространству и по времени будут между собой совпадать. И для функции, сдвиг у которой происходит в противоположную сторону, вторая производная по времени со второй производной по пространству тоже совпадает. В качестве иллюстрации, можно показать, что участок с постоянным ускорением в пространстве выглядит как участок параболы, и если на графике компенсировать постоянную скорость, то относительно точки с этой скоростью график будет симметричен.

Когда говорится о равенстве вторых производных, речь о раздельных направлениях пространства и времени. Направления, совмещающие направления перемещения гребня в пространстве и времени — ведут к неизменности функции, а значит, и нулевым производным вдоль них. Зато, в других совмещениях направлений, в которых пространственное направление противоположно направлению распространения, множитель результата второй производной может доходить до двух.

Если мы возьмём функцию, вторая производная по пространству и вторая производная по времени у которой совпадает, то она позволит существовать не только профилю, движущемуся вправо, или профилю, движущемуся влево, но и функции, которая представляет собой сумму таких профилей. Это и есть дополнительная особенность волны: возможность прохождения через одну точку нескольких профилей в разных направлениях.

Формула волны это равенство второй производной по времени и второй производной по пространству.

Расширение на многомерное пространство выглядит так: для каждого пространственного направления, с различием противоположных направлений, задан свой отдельный профиль, включающий и данные для отрицательных отступов. Такие профили движутся во времени по своим направлениям с одинаковой скоростью.

Где  — все пространственные координаты.
 — направление в пространстве.
 — величина проекции координат на выбранное направление.

Пространственная производная зависит от направления дифференцирования. Общая пространственная производная это вектор, проекция которого говорит о производной в заданном направлении. Вторая производная в прямом и обратном направлении совпадает, общая вторая производная по пространству это число.

Общая вторая производная по пространству это сумма вторых производных по отдельным координатам.

Если отношение значения функции и второй производной для всей области определения постоянно и отрицательно, то функция будет характеризоваться частотой. Коэффициент, отражающий отношение значения и второй производной, будет минус квадрат частоты.

У волн с определённой абсолютной величиной частоты может различаться как знак частоты, так и пространственное направление. В одномерном случае существует четыре вида функций, подходящих под это уравнение, с одним модулем частоты, но с различной зависимостью от времени и от пространства.

Каждый профиль может состоять из набора произвольных комплексных значений, но можно внести дополнительное ограничение. Чтобы профиль, сдвигающийся в положительную сторону, имел в составе только положительные частоты. То есть, сделать так, чтобы знак частоты у каждой составляющей одновременно указывал и сторону распространения, а волн, в которых пространственное направление распространения противоположное, а частота составляющих та же самая, не было.

Другими словами, исключить «сопряжённые волны». И тогда два профиля противоположного направления будут иметь раздельные частотные диапазоны и могут быть совмещены в один профиль, с общим преобразованием по времени.

Частота у частотных составляющих при указания смещения фазы при движении во времени ставится под модуль. Тогда с течением времени части функции, соответствующие положительным и отрицательным частотам, сдвигаются в пространстве в противоположных направлениях.

У движущихся навстречу профилей в одномерном пространстве можно отметить два эффекта:

1. Эффект отражения. Если встречные профили одинаковы вдоль своих собственных направлений, за исключением противоположного знака, то можно найти точку, в которой у профилей совпадают внутренние координаты, сумма в ней приводит к нулю. Эта точка будет приводить к зеркальному эффекту: профиль идущий на эту точку будет как бы отражаться и идти обратно, поменяв знак.

2. Эффект стоячих волн, когда встречные гармонические колебания одной частоты периодически, то гасят друг друга в ноль, то складываются в гребни и впадины, при этом образуя узлы постоянных нулевых значений и пучности колебаний двойной амплитуды, не сдвигаясь ни в одну из сторон. В пространственно-временном распределении это выглядит как сетка из линий нулевых значений вдоль пространства и времени, в квадратных ячейках которой присутствуют гребни, знак которых определяется в шахматном порядке.

При введении ограничения на частоты стоячих волн не будет. Например, такого, чтобы вся плоскость была нулевой, за счёт того, что встречные профили друг друга полностью гасят, а в следующий момент волны появляются — уже не случится. Здесь в отсутствие реальной составляющей о существовании волны будет говорить мнимая составляющая, и наоборот. Общий результат встречных гармонических волн одинаковой амплитуды будет синусоподобная функция, с общим коэффициентом зависимости от времени вида .

Из-за введённого ограничения все пространственные частоты, и положительные и отрицательные, относительно времени становятся отрицательными, вращение в комплексной плоскости частотных составляющих при движении во времени выполняется в одну сторону.

Для положительных частот вращение во времени идёт в обратном направлении по отношению к вращению в пространстве. Пояснить это можно на примере болта. У болтов правосторонняя резьба, и чтобы закрутить, нужно крутить болт вправо, по часовой стрелке. Но при закручивании гребень волны приближается к шляпке болта, вместе с прикручиваемой деталью. Поэтому, для того чтобы гребень волны отдалялся, вращение нужно производить в противоположную сторону. Отрицательные частоты и в пространстве закручиваются, наоборот, против часовой, и во времени вращение идёт против часовой, что приводит к отрицательному направлению движения в пространстве.

Если мы видим отсутствие мнимой составляющей у среза функции на определенный момент, это значит, что мнимые составляющие противоположных частот погасили друг друга. В следующий промежуток времени один профиль разойдётся на два одинаковых, движущихся в противоположных направлениях, с появлением противоположных мнимых составляющих.

Добавление ограничения частот делает производную по времени характеристикой, включённой в пространственное распределение. Вместо содержания отдельно состояния и отдельно данных о его изменении, всё содержится в функции в пространственном распределении, в комплексных значениях. Ограничение возможных состояний приводит к более тесной взаимосвязи составляющих.

Потоки и их столкновение

Перемещение профилей можно воспринимать как поток, как размеренную передачу некоторого ресурса на расстояние. Величина потока больше связана с изменением значения функции, чем с самим значением, так как при постоянном значении можно сказать, что передачи не происходит.

Поток в виде постоянной передачи в случае одномерной функции с действительным значением выглядит как 

Производная и по пространству и по времени с точностью до знака даёт величину . Но в таком случае значение функции с течением времени выходит за любые рамки.

Если для функции использовать комплексные значения, то постоянная скорость изменения может быть постоянной не сама по себе, а с учётом перпендикулярного движения в качестве изменения фазы, вращения. И тогда чистый поворот в комплексном пространстве будет одновременно и постоянным изменением и изменением ограниченным.

Для двумерного пространства постоянное рассеяние ресурса из точечного источника выражается в распределении величины значения и производной по времени обратно пропорционально расстоянию от источника.

Поток можно интегрировать по контуру вокруг источника с учётом локального направления: интегрировать производные отдельно по составляющей вдоль и отдельно по составляющей поперёк контура.

Интеграл по контуру с заданным расстоянием от источника приводит к постоянному суммарному значению функции, постоянному суммарному значению производной по времени и постоянному суммарному значению пространственной производной относительно контура, что значит, что поток при расхождении сохраняется.

Интересно, что не смотря на то, что распространение занимает время, при условном смещении общего уровня на  такое распространение выглядит как мгновенное.

Если величина потока из источника будет зависеть от времени нелинейно, эффекта мгновенности не будет, но интегрально поток на постоянном расстоянии будет равен потоку источника в соответствующий момент.

При действительной функции несколько источников постоянного потока при таком интегрировании по любому контуру, включающему источники, дают сумму величин исходящих потоков.

Если заменить постоянно изменяющиеся действительные потоки на постоянно вращающиеся комплексные, то можно заметить, что при одном источнике для постоянного потока постоянной частоты интеграл по контуру постоянного радиуса даст одно и то же значение, с фазой, которая прямо соответствует фазе источника в момент испускания. То есть, интеграл совпадает с величиной испускания, также, как и в случае действительной функции.

Но если центр у контура интегрирования в виде окружности сместить, то у суммарного потока значение уменьшится, кроме векторного сложения значений произойдёт и комплексное гашение амплитуды, из-за размытия фазы.

Для нескольких разнесённых источников с колебаниями в одинаковой фазе потоки будут накладываться так, что интеграл и значений и производных по окружающему контуру всегда будет меньше, чем сумма потоков самих источников.

Конечно, интересный вопрос, куда исчезает поток, и не стоит ли компенсировать это через различие фаз, а то и изменение амплитуд? Нормировку какую-нибудь произвести… Но есть и более важный вопрос. А ничего, что представленное двумерное рассеяние уже не выполняет волновое уравнение?

Похоже, с двумерным распределением потока волн не так всё просто.

Если взять интеграл по контуру от производной вдоль радиуса, для функции, заданной как распределение волны одной частоты с рассеянием обратно пропорционально расстоянию, получим

При вычислении такой общей для одинакового отступа производной получено дополнительное слагаемое. А это значит, что для соблюдения волнового уравнения рассеяние должно его учитывать, и значит, отличаться от простой зависимости «обратно расстоянию».

Самые простые волны для рассмотрения это плоские. Плоская волна характеризуется тем, что колеблется в пространстве вдоль только одного направления, вдоль всех поперечных направлений она постоянна. Для изучения потоков можно разобрать, как накладывается две плоские волны одной частоты разных направлений.

Первая производная вдоль , вместе с самим значением, будет иметь коэффициент, меняющийся как удвоенный косинус вдоль .

Частота вдоль снижена до . Интеграл у такой производной вдоль будет колебаться около нуля. Похоже, даже частичная встречность потоков требует развития методов расчёта величины суммарного потока.

После расхождения потоки выглядят точно так же, как выглядели бы без наложения, какими сошлись, такими и разошлись. Так что, само распределение потоков при их наложении можно описать как сохранение суммарной величины потока, но с перераспределением отдельных частей вдоль поперечной координаты, в виде коэффициента, создающего области обнуления и области удвоения, обоих знаков. При расхождении это перераспределение возвращает потокам поперечную составляющую.

Рассмотрим ситуацию с двумя точечными источниками волн. Здесь можно предположить, что накладываясь, волны не гасят, а плавно перераспределяют потоки друг друга, изменяют направление распространения, это как мягкая форма такого же перераспределения, которое было в примере с плоскими волнами. На поток будто наложен множитель, оставляющим неизменным суммарное значение по контуру, но производящий перераспределение. И волны в результате даже в некоторой степени концентрируются в общем направлении, подобно лучу лазера, который с расстоянием не рассеивается.

При таком перераспределении суммарная величина потоков должна сохраняться. Наложение колебаний увеличивает удельный поток в месте концентрации, поток переходит туда из мест взаимного гашения. И результат наложения с эффектом концентрации будет превышать результат расчётного наложение волн, рассеянных обратно расстоянию. Но разве амплитуда наложения двух волн может быть больше амплитуд по отдельности? Если рассеяние правильное, то нет.

Правильное — это какое? Суммарно по контуру амплитуда может и не сохраняться.

Самое время разобраться, что именно сохраняется у волны при распространении.

Иллюстрация того, как волны одной частоты от двух источников влияют на максимальную высоту волны в других местах.

Разумеется, при распространении волн сохраняется энергия.

В примере с двумя плоскими волнами энергия двух потоков перераспределяется в энергию двух видов: кинетическую — которая при сложении потоков сложилась не как вектор, а как два числа, и потенциальную, которая в сложенном виде не проявлена, но при расхождении потоков возвращает вклад в поперечное направление.

В гребне волны энергия тоже двух видов: потенциальная, в виде возвышения гребня, и кинетическая, в виде скорости изменения. Скорость входит в энергию как квадрат величины, . У плоской гармонической волны поток энергии постоянный, поэтому там, где скорость нулевая, уже квадрат отклонения компенсирует недостающую часть энергии, но с коэффициентом, равным квадрату частоты.

Энергия это действительная величина, её можно считать отдельно для каждой комплексной составляющей, тогда фаза результата не будет удвоена.

Получается, для получения распределения энергии можно либо возвести в квадрат гармоническую функцию, предварительно умножив на частоту, либо возвести в квадрат вторую производную гармонической функции, предварительно поделив на частоту, либо взять со знаком минус произведение функции и её второй производной, что подходит для любых функций.

Общая амплитуда входит в энергию как квадрат величины. Значит, при складывании одинаковых функций суммарная энергия возрастёт в четыре раза. При этом, совсем не пересекающиеся функции дают вклад в энергию линейно, энергией суммы будет сумма энергий. Это значит, что когда при совмещении двух функций требуется сложить энергию, принцип совмещения самих функций уже не является суммой. В таком совмещении для сохранения энергии требуется сбалансировать не только пару функций, а одновременно пару функций и пару их вторых производных. Или пару первых производных по времени, но в квадрате.

Производная по пространству это две составляющих вектора, каждая из которых комплексное число, а в целом это кватернион. А значит, на одну амплитуду приходится три раздельных фазы. Совмещать квадраты двух кватернионов в квадрат третьего меня жизнь не учила, но вполне можно обнаружить, что октонион, как показатель, что куда переходит, на одну амплитуду имеет семь фаз. Не самое удачное время вернуть сопряжённые волны, ведь тогда на горизонте будут седенионы, а там с делением составляющих на амплитуду и фазу уже не всё так просто.

Аппроксимация точечными источниками

Если точечные источники с одной фазой излучения выстроить в ряд, то из всех направлений будет выделяться одно. Для излучения сразу всем рядом в других направлениях нужно сдвигать фазу, в линейной зависимости от позиции в ряду, иначе для этих направлений одинаковая излучаемая фаза будет восприниматься вразнобой, и от этого суммарные волны погасят свою амплитуду.

Подсчитать, как точечный источник излучает гармоническую волну можно двумя способами.

Первый способ.
Сбор волны через сложение профилей для каждого направления полностью согласуется с уравнением волны. От точечного источника излучение волны идёт сразу во все стороны, во всех профилях точка даёт одинаковый вклад. Смещённые в пространстве и времени профили дают вклад обратно в функцию. Так как профиль влияет на соседние направления как проекция, то есть, с растяжением обратно степени сходства направлений — значит, с умножением аргумента гармонической составляющей на степень сонаправленности — то для получения результата суммирования профилей для выбранной частоты нужно проинтегрировать экспоненту с умножением мнимого аргумента на косинус интегрируемого угла.

Осталось избавиться от отрицательных частот, тогда появится ещё и мнимая составляющая.

Существует формула для вычисления этой функции без интеграла.

Второй способ.
Сначала нужно выяснить, как выглядит вторая производная по отдельной координате от произвольной функции радиуса.

Затем сложить вторые производные для обеих координат.

При выборе одной частоты будет верно, что 

Но, так как выполняется симметрия масштаба, можно решить с единичной частотой, а затем функцию просто масштабировать.

Решая это дифференциальное уравнение Бесселя, получим функции, которые в реальной части совпадают с результатом первого способа. Если исключить из решения встречное направление потока, от двух констант останется одна

Полученная функция затухает пропорционально квадратному корню расстояния, но в точности с таким распределением не совпадает. Неравномерность отношения есть и в амплитуде и в фазе. В представленном виде общий сдвиг фазы , в нуле сдвиг увеличивается ещё на . Амплитуда отношения стремится к . В нормализованном для приближения к  виде функция будет:

Если считать, что волны рассеваются обратно расстоянию, то волны, рассеивающиеся обратно корню от расстояния — на одинаковых расстояниях, начиная с определённого, имеют бо́льшие значения, и их превышающую часть можно считать переизлучением. Правда, тогда вблизи источника обнаруживается и область, где переизлучение отрицательное.

А сами функции Бесселя по модулю в области нуля даже ещё меньше такого рассеяния.

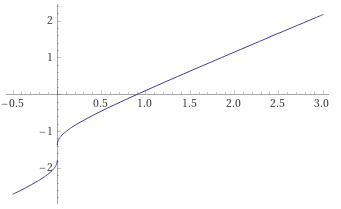
Фаза функции Бесселя.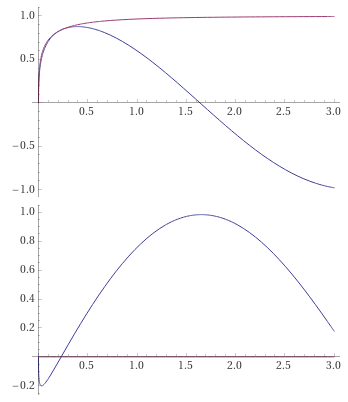

Нормализованная функция Бесселя с компенсацией рассеяния и сдвигом фазы. Видно падение амплитуды в районе нуля. Комплексные составляющие на отдалении больше 0.5 становятся сходны с косинусом и синусом.
Для отрицательных аргументов функции в мнимой составляющей можно задать удвоенное значение , чтобы в паре с ней в области отрицательного аргумента изменить знак у реальной части, чтобы волна на отрицательной стороне не была сопряжённой. При компенсации рассеяния функция Бесселя умножается на корень аргумента, для отрицательных значений это будет мнимое число, производящее сдвиг фазы на четверть оборота. Выбором знака корня можно выбрать положительную или отрицательную сторону сдвига.

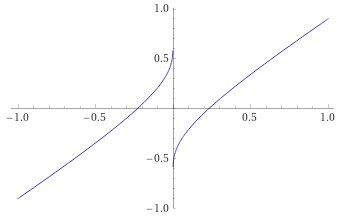Фаза функции Бесселя с компенсацией рассеяния и выбором такого знака у компенсирующего множителя, который выравнивает фазу.
Участок замкнутого контура можно представить состоящим из точечных источников, которые повторяют амплитуду и фазу пришедшей на них гармонической волны от источников изнутри контура. Во внешнем пространстве это будет хорошим приближением волны, за исключением излучения краёв, которое проявляет себя вплоть до добавления оставшихся участков замкнутого контура. В случае замыкания контур сработает как зеркало внутрь, повторитель наружу. Распределение излучения точечных источников должно быть функциями Бесселя, тогда это будет точное представление принципа Гюйгенса.

Концентрические волны

В дифференциальном уравнении координата может быть интерпретирована как величина обратная степени скругления перпендикулярной координаты. Степень скругления, она же степень приближения к центру, будет обозначаться .

По любой функции и её производной можно определять локальную частоту вдоль направления, имеющую для каждой точки своё отдельное значение.

Локальная частота может быть комплексной — при изменении амплитуды вдоль направления дифференцирования, в том числе при неравномерном изменении фазы.

Вторые производные можно представить через значение функции и локальную частоту

Координата используется как проекция координаты , с условием, чтобы .

По этим равенствам видно, что  должно быть комплексным. Значит, частота тоже комплексная.

Частотная характеристика энергии делится на две комплексные величины, у которых мнимые части в сумме дают ноль. Эти комплексные величины в роли производных отражаются в негармоническом изменении амплитуды и фазы вдоль перпендикуляра к округлому фронту.

Расхождение фаз у функции и у второй производной по отдельному направлению говорит о процессе концентрации или рассеивании потока вдоль этого направления. Общая вторая производная, суммарная по координатам, при этом может оставаться в той же фазе, отличаясь разве что знаком.

Взаимосвязи

Выполнение волнового уравнения не подразумевает источников потока. Приходится делить одну функцию на две, в отдельном виде выполняющих уравнение везде, кроме областей перевода потока с одной на другую. Относительно источника это внутренний и внешний уровень.

На внутреннем уровне точечного источника волна также центрально-симметрична, только наоборот, концентрируется со всех сторон в одну точку. Можно подробно представить такую волну: так как суммарно энергия по одному значению радиуса постоянна, то постоянен по модулю и окружающий интеграл квадрата значения, умноженного на квадрат частоты, а значит, если локальная частота не меняется, то амплитуда меняется обратно корню от расстояния.

Чтобы разобраться во взаимосвязях можно отметить две особенности в распространении волн.

1. Общая ситуация при простом сложении двух функций это изменение энергии: возможно как дополнительное усиление в два раза, так и полное гашение. Так как при позитивном сложении энергия должна сохраняться, то при суммировании требуется использовать коэффициенты, причём, комплексные. Коэффициенты срабатывают так, что сколько суммарно энергии было в функциях, столько и осталось, но пропорция здесь — это уже отношение двух комплексных чисел, а значит, включает не только количественное отношение, но и степень расхождения фаз, дополнительную вариацию. При выбранной пропорции смешивания вариация разности фаз может отражаться на вариации усиления амплитуды. Можно отметить, что для отдельных двух плоских волн, если у них различаются направления или частоты, коэффициенты не нужны. Если и направление и частота совпали, коэффициенты зависят от различия фаз. Если у волн присутствуют и другие составляющие, то отдельный вклад плоских волн зависит от общих коэффициентов, они же общие.

2. Два представления: представление волны в пространстве как суммы профилей и представление отдельных профилей в координатах угол-сдвиг — были эквивалентными. Но после разбора круговых волн стало ясно, что это не совсем так. При округлении фронта во вторую производную в направлении перпендикулярном радиусу просачивается энергетический вклад из первой производной по радиусу, и этот вклад должен быть скомпенсирован. В представлении угол-сдвиг профили не просто движутся через линию, означающую схождение в точку единым фронтом, а изменяют свою величину — добавляется множитель, сохраняющий энергию при концентрации. Значит, для полного представления волны к данным о профилях должны быть добавлены данные о местах концентрации и о соответствующих множителях.

Добавление источников в волновые процессы добавляет и распределённые множители в профили. Получается, нельзя в профильном представлении просто перекидывать значение на другой уровень по достижению п

© Habrahabr.ru