Как с помощью хакатона столкнуть математиков и ML–щиков, и кто тогда победит29.11.2020 08:33

Введение


Эта статья о том, как мы совместно с роснефтёвой «дочкой» «Самаранефтехимпроект» и Казанским Федеральным Университетом в сентябре 2020 года провели «Хакатон трёх городов», на котором предложили студентам решить классическую задачу сейсмической корреляции отражающих горизонтов. С такими задачами постоянно сталкиваются специалисты по сейсморазведке по всему миру. Для участников задачу решили преподнести как «задачу поиска оптимального пути», чтобы не отпугнуть студентов страшными словами. В статье расскажем подробнее про задачу и разберём интересные решения участников. Это будет увлекательно для специалистов как по прикладному математическому моделированию, так и машинному обучению и анализу данных.

Организационная часть


Интересные подробности организации онлайн-хакатона в трёх городах мы рассказали в статье на vc.ru — Нефтянка и хакатон. Марафон — это не только бег.
Упомянем лишь, что для онлайн-формата мы выбрали сервис Discord и оставим ссылку на правила хакатона (ссылка на площадке Boosters).

Постановка задачи


В сейсморазведке существует понятие «сейсмический отражающий горизонт» — это устойчивая по динамике и площади распространения отражённая волна, которая соответствует определённой геологической границе. Корректно проведя обработку полевых сейсмических данных и распознав (специалисты по сейсморазведке говорят — «проинтерпретировав») сейсмические горизонты, можно с точностью до 5–10 метров определить глубины их залегания. Определив глубины, далее можно уже вместе с геологами привязать данные горизонты к геохронологической шкале (Геохронологическая шкала — Википедия) и распознать их более мелких собратьев. А после чего решать — между какими горизонтами могут залегать ловушки с нефтью, как выглядит рельеф структурной модели месторождения и др.

image

Вертикальные сечения сейсмического куба и распознанные сейсмические отражающие горизонты

На практике горизонты выделяются послойно на сейсмических разрезах сейсмического куба — как вручную, с помощью расстановки (специалисты по сейсморазведке говорят — «пикирования») большого числа реперных точек, так и с помощью автоматизированных и полуавтоматизированных процедур поиска. Безусловно, качественное решение задачи интерпретации сейсмических горизонтов с помощью программного обеспечения крайне востребовано и позволяет существенно снизить временные затраты специалистов по сейсморазведке.

В то же время, изучение источников (Least-squares horizons with local slopes and multi-grid correlations, Waveform Embedding: automatic horizon picking with unsupervised deep learning) показывает, что разработанные алгоритмы и решения основаны на небольшом числе математических подходов, поэтому мы решили попробовать привлечь студентов с их ещё не затуманенным научными изысканиями сознанием и предложить им данную задачу в форме задачи поиска оптимального пути на сложной поверхности.
В итоге задача была сформулирована так: построение пути движения на сложной поверхности, проходящего через заданные точки и удовлетворяющего условиям минимума некоторого функционала, зависящего от длины пути и его углов (градиентов).

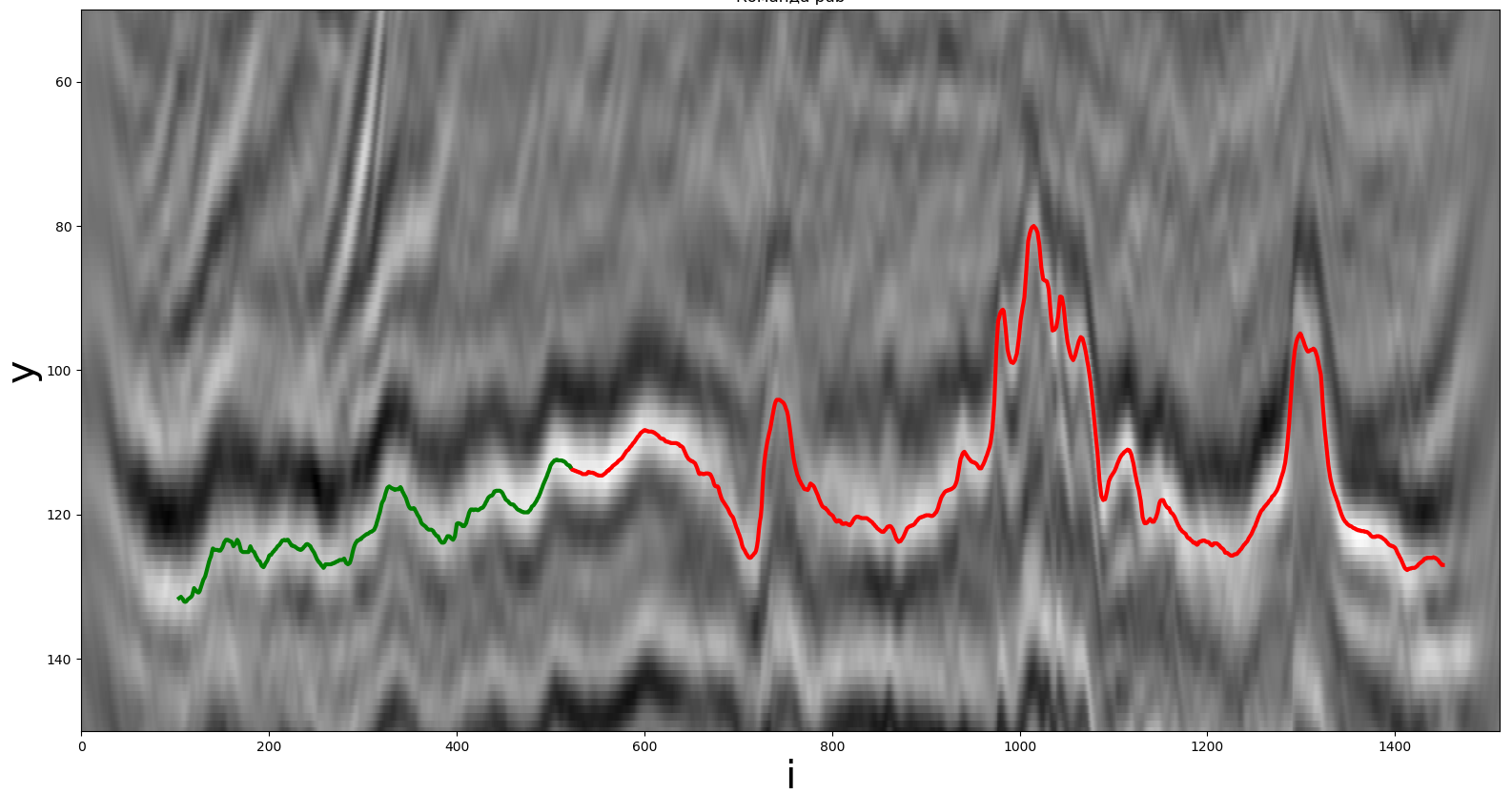
image
Пример части исходного сейсмического разреза для построения горизонта. Зеленая линия — заранее известная часть, красная — искомая.

Участникам соревнования предстояло за 12 часов найти решение, позволяющее продолжить путь по оптимальной траектории на скрытой части датасета. На валидацию решения предоставлялось 20 попыток, побеждал участник с минимальным значением метрики.

Подробное описание данных
Ниже подробное описание данных, которые были доступны участнику:
  1. Карты поверхностей. Двумерные массивы, в ячейках [x, y] которых находятся значения z (x, y) высот поверхностей.
  2. Координаты (x, y) путей для обучения в двух областях L1 и L2. Таблица со столбцами x, hor_1, …, hor_4. 
  3. В области L2 полностью доступны 4 пути (1, 2, 3, 4), в области L1 — 3 пути (1, 3, 4). 2-й путь области L1 доступен частично (40%). Оставшиеся 60% этого пути необходимо найти.

image
Визуализация всех данных, которые были доступны участнику — 2 сейсмических среза с горизонтами.

По-простому, участнику надо было продолжить hor_2 в области L1. Область L2 представляла собой перпендикулярный срез L1. Мы её добавили для генерации участниками дополнительных знаний. Но, к сожалению, она не пригодилась участникам.


На протяжении соревнования турнирная таблица строилась на основе значений метрики на публичной части тестовых данных. После окончания соревнования значение метрики было пересчитано на приватной части, и турнирная таблица была обновлена. Это важно для того, чтобы получить устойчивые решения, то есть не только подогнанные под публичные данные, но и способные показать сопоставимый результат на приватных. Оказалось, что это было сделано не зря, и после финальной оценки качества турнирная таблица изменилась.
Для количественной оценки полученных результатов использовалась следующая метрика:

$F\left (\widehat{y},\widehat{z} \right ) = \sqrt{\sum_{i=0}^N\left(\widehat{y}_{i}^{pred} -\widehat{y}_{i}^{etalon} \right)+\left(\widehat{z}\left(i,y_i^{pred}\right) - \widehat{z}\left(i,y_i^{etalon} \right) \right)^2} $


где:
N — размерность искомого горизонта;
${y}_{i}^{pred}$ — координаты горизонта, полученного с помощью алгоритма, $i\in\overline{0,N}$;
${y}_{i}^{etalon}$ — координаты эталонного горизонта;
$\widehat{z}\left(i,y_i\right)$ — значения карты поверхности в точке с координатамиi, yi;
$\widehat{y}_i = \frac{y_i}{{height}}$, где height — максимально возможное значение координаты y карты поверхности;
$\widehat{z}\left(i,y_i\right) = \frac{z\left(i,y_i \right)}{{max \left(z \right)}}$, где max (z) — наибольшее значение карты поверхности.

Реализация метрики в Python 
def score(true, submission, all_data):
   #true – pandas.Dataframe с истинными значениями пути;
   #submission - pandas.Dataframe со значениями пути, построенного
   #Участником;
   #all_data - numpy.ndarray со значениями высот поверхности
   all_data = all_data.astype('float64')
   # Наибольшее значение карты поверхности
   max_z = abs(all_data).max()
   # Построенный участником путь
   y_pred = submission.loc[idx.index.values].y.values.astype('int')
   # Истинный путь
   y_true = true.y.astype(int)
   # Значения высот поверхности построенного пути
   z_pred = all_data[true.index.values.astype(int), y_pred.astype(int)]
   # Значения высот поверхности истинного пути
   z_true = all_data[true.index.values, y_true]
   # Слагаемые функционала ошибки
   y_err = ((y_pred - y_true)/3000)** 2
   z_err = ((z_pred - z_true)/max_z) ** 2
   # Итоговое значение метрики качества модели
   total_err = np.sqrt(np.sum(y_err + z_err))
   return total_err


Какие методы применяли команды


Задача подбиралась изначально такой, которую можно было бы решить несколькими способами: прямым и обратным (классическими математическими методами и методами машинного обучения соответственно).

С точки зрения машинного обучения задачу можно решать двумя методами:

1) Построение регрессии
Используя известные пары точек ($x_i,y_i$), можно построить отображение $f:\phi \left(x_i \right)\mapsto y_i$ путём минимизации функции потерь L. $\phi \left(x_i \right)$ — признаковое описание i-й точки.

Например, $\phi : x_i \mapsto x_i$ или $\phi : x_i \mapsto \left( x_i,x_i^2,x_i \cdot x \right)$

Функцией потерь может быть как исходная функция ошибки из постановки задачи, так и более простая функция, например, среднеквадратическое отклонение построенного и исходного путей:

$\frac{1}{N} \sum_{i=0}^N \left( y_i - \widehat{y}_i \right)^2$

Для построения отображения f можно воспользоваться множеством популярных методов машинного обучения: начиная с полиномиальной регрессии, проходя через случайный лес и глубокими нейронными сетями.

Несколько команд использовали этот подход, используя в качестве $\phi$ свёрточную или полносвязную нейросеть, а в качестве f — нейронную сети или гауссовские процессы.

2) Семантическая сегментация

image
Пример семантической сегментации

Исходную задачу можно решать как задачу компьютерного зрения. Точки (x, y) рассматривать как пикселы изображения, где всё изображение — это весь датасет, а «яркость» пиксела (x, y) — значение z (x, y). Для построения пути нужно каждому пикселю присвоить один из классов — 0 или 1. Часть изображения, находящаяся ниже пути или включающая его, относится к классу 0, а оставшаяся — к классу 1. Бытовое решение для такой задачи — полносвёрточная нейросеть U-Net, на вход получающая кусок (патч) исходного изображения и выдающая массив того же размера, состоящий из нулей и единиц, обозначающих классы соответствующих пикселов.

Кроме методов глубокого обучения, для сегментации изображений можно также использовать методы классического компьютерного зрения и обработки изображений, например, Flood fill. Это и сделал один из участников, тем самым предобработав изображение для дальнейшего применения алгоритмов поиска кратчайшего пути.

С точки зрения классических математических методов предложенная задача является классической задачей оптимизации, и мы наблюдали попытки её решения следующими группами методов:

  1. Методы, использующие принцип локального экстремума;

    Суть данного подхода заключается в поиске локальных экстремумов значений поверхности в пределах заданного окна поиска. Далее выбирается то значение координаты y среди найденных экстремумов, которое наименьшим образом отличается от y, найденного на предыдущем шаге.

  2. Методы, использующие принцип глобального экстремума;

    В рамках данного подхода при определении координаты $y_i$ ищется глобальный экстремум среди усреднённых значений поверхности карты в пределах заданного окна поиска.

  3. Методы, основанные на минимизации заданной эвристики.

    Данным подходом воспользовалось несколько команд, суть данного подхода заключается создании и минимизации предложенного командами функционала.


Итоги и кто победил


Для начала разберём решения участников.

Методы машинного обучения:
Одним из решений была авторегрессионная свёрточная нейросеть, выдающая вещественное число — значение пути $\widehat{y}_i$ для i-го шага. На вход нейросети подавались патчи 32×32 пиксела исходного изображения. В качестве функции $\phi$ для извлечения признаков использовалась предобученная свёрточная нейросеть ResNet34. Полученное этой нейросетью признаковое представление объединялось со значениями данного пути с предыдущих 32 шагов. Для прогнозирования дальше 32 шагов в качестве предыдущих значений горизонта использовались предыдущие прогнозы нейросети. Нейросеть обучалась модификацией стохастического градиентного спуска Adam с экспоненциальным уменьшением шага оптимизатора по мере обучения. Для обучения минимизировалось среднее абсолютное отклонение (эксперименты со среднеквадратическим отклонением дали хуже результат). Во избежание переобучения использовался Дропаут, то есть случайное обнуление части нейронов. Для обучения нейросети потребовалось около 10 минут, 20 полных проходов по всему датасету и 720 шагов оптимизатора.

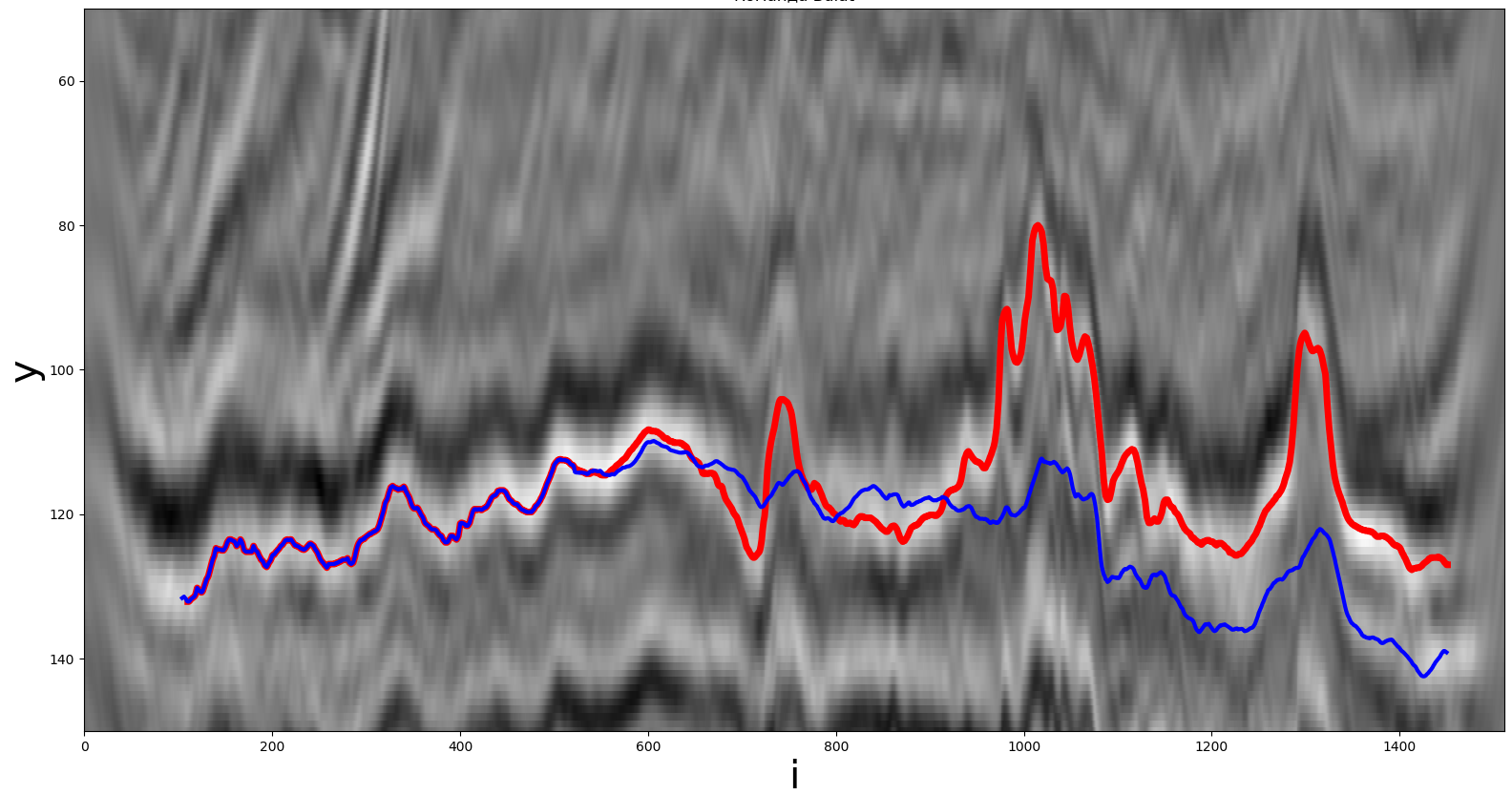
image
Решение, полученное с помощью свёрточной нейросети. Красная линия — реальный путь, синяя — полученный участником.

Прогноз нейросети занимает около 1 минуты на CPU AMD Threadripper 2950x и GPU Nvidia GTX 1080 Ti.

Результат нейросети (метрика) — 5.71 на публичной турнирной таблице. Также были проделаны эксперименты с заменой свёрточной нейросети на рекуррентную, но её результат был хуже. В итоге в качестве финального решения были использованы классические методы вычислительной математики.

Кроме законченных решений, участники также поделились своими идеями, которые не успели реализовать из-за жёстких временных рамок соревнования и вычислительной сложности их задумок. Некоторые из них пытались применить нейронные сети, но, потратив большую часть времени, переходили к более простым и эффективным алгоритмам или даже к грубому перебору и правилам, что в итоге дало лучший результат и привело к призовым местам.

Также ряд интересных решений основан на знаниях из других дисциплин: например, классическое компьютерное зрение и обработка изображений, теория графов, анализ временных рядов. Одна из команд даже поставила задачу в терминах обучения с подкреплением, про которое вы могли слышать, и придумала решение, но, к сожалению, не успела его реализовать.

Классические математические методы:

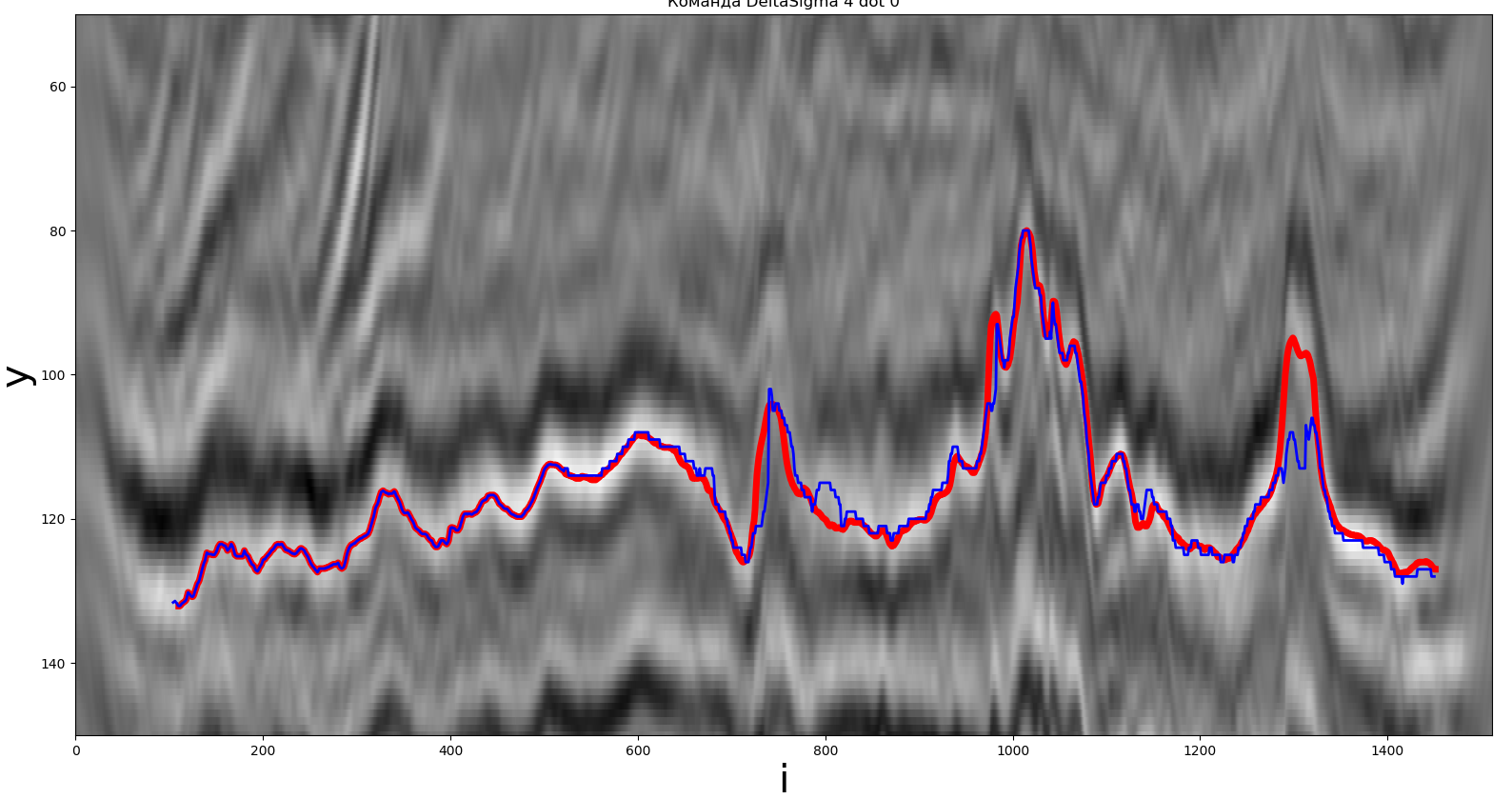
image
Одно из решений, полученное методом локального экстремума. Красная линия — реальный путь, синяя — полученная участником.

Для данного метода в качестве экстремума использовался локальный максимум. Синим цветом отмечен построенный участниками путь, красным — искомый горизонт. Подробное описание представлено ниже.

$y_{i+1} = min \left| j-y_i \right|, \forall i \in \overline{0,N-1}, j \in \Omega,$
$\Omega = \left \{ m|z(i,m)> z (i, m-1) \cap z (i, m) > z (i, m+1), \forall m \in \overline {m_1, m_2} \right \}$» />, <br /><img src=,
$m_2=min(height - 1,y_i + size_y$,
где:
$height$ — максимально возможное значение координаты y карты поверхности;
$size_y$ — размер окна поиска.

Метод реализован на языке Python. Время работы составило порядка 0.103 секунд, F (y, z) = 1.57, $size_y$= 100.

Вывод: метод достаточно прост для реализации, время работы не превышает 0.1 секунды.

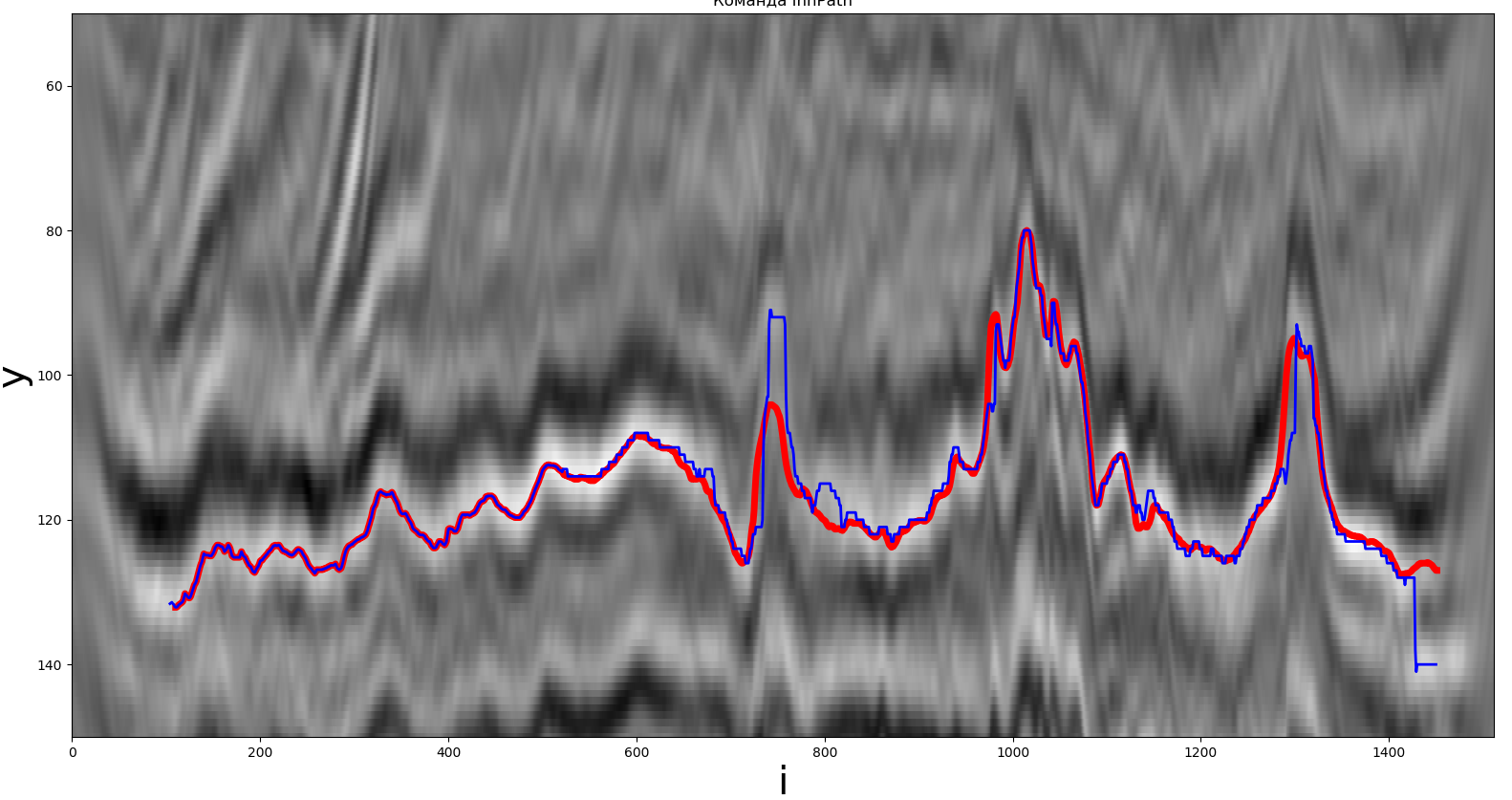
image
Одно из решений, полученное глобальным экстремумом. Красная линия — реальный путь, синяя — полученный участником.

Перейдём к следующей группе. Как и ранее, в данном методе максимум использовался в качестве экстремума.

$y_i= {argmax}\left(\frac{1}{size_x} \sum_{{j=0}}^{{size_x-1}}z (i+j,m))\right), \forall i \in \overline {0,N}, m \in \overline{m_1,m_2}$,
$m_1 = max(1,y_i - size_y)$,
$m_2=min(height - 1,y_i + size_y)$,
где:
height  — максимально возможное значение координаты y карты поверхности;
$size_x,size_y$ — размер окна поиска.

Метод реализован на языке Python. Время работы составило порядка 0.19 секунд, F (y, z) = 1.97, $size_x$= 9, $size_y$= 21.

Вывод: метод достаточно прост для реализации, время работы не превышает 0.2 секунд.

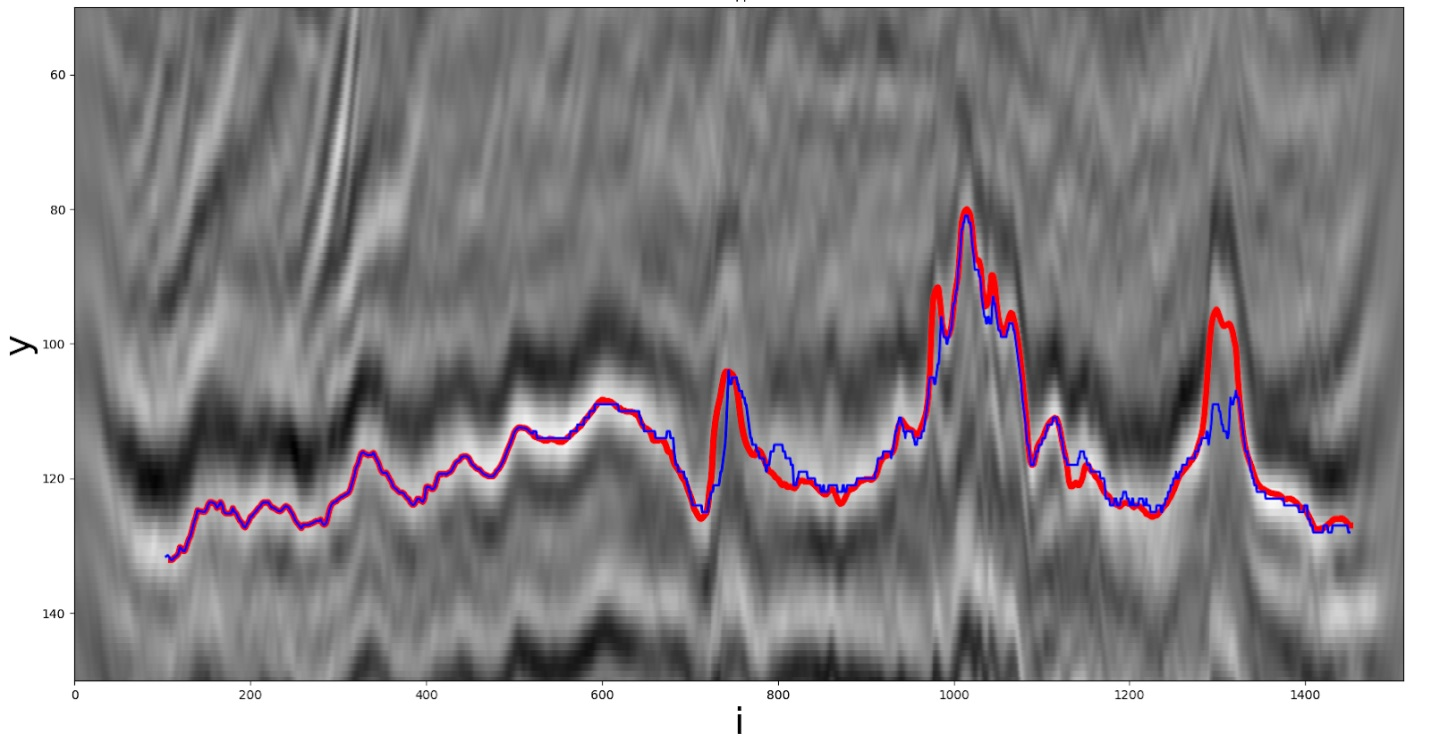
image
Одно из решений, полученное эвристикой. Красная линия — реальный путь, синяя — полученный участником.

Рассмотрим последнюю группу методов. Как уже говорилось ранее, очередная координата $y_i+1$ ищется по минимуму функционала в пределах заданного окна поиска.

Ниже представлен один из функционалов, предложенных командами. С математической точки он выглядит следующим образом:
$y_{i+1}= {min}\left(\frac{(z(i,j)-z(i,y_i))^2}{max^2(z)} + \alpha \frac{(j-y_i)^2}{{height}^2}\right), \forall i \in \overline {0,N-1}, j \in \Omega,$
$\Omega = \left \{ m|z(i,m)>z (i, m-1)\cap z (i, m)>z (i, m+1), \forall m \in \overline {m_1, m_2} \right \}$» /><br /><img src=,
$m_2=min(height - 1,y_i + size_y)$,
где:
$height$ — максимально возможное значение координаты y карты поверхности;
$\alpha$— коэффициент, отвечающий за влияние ошибки по y на значение функционала;
$size_y$ — размер окна поиска;
$max(z)$ — наибольшее значение карты поверхности.
Метод был реализован на языке Python. Время работы составило порядка 0.12 секунд, F (y, z) = 1.58, $size_y$= 50, $\alpha$= 15000.7.

Вывод: время работы метода не превышает 0.15 секунд.

Методы всех трех групп показали достаточно близкие результаты на заданном наборе данных. Наименьшее значение метрики (1.57) было достигнуто методом, основанным на поиске локальных экстремумов значений поверхности в пределах заданного окна поиска.

Заключительная часть


К сожалению, к концу хакатона почти все новаторы перешли на темную сторону переквалифицировались и стали консервативно настроенными, то есть стали отправлять решения на классических алгоритмах… и победили консерваторы.

Мы хотели объединить участников из двух областей: вычислительной математики и машинного обучения. Одни привыкли работать с неструктурированными данными неизвестной природы, другие — изучать физические процессы и строить на их основе математические модели. Чтобы увеличить разнообразие идей и решений, мы кратко рассказали, как были получены данные. Это одна из причин, по которой решение на основе простых численных методов дало лучшие результаты. Второй причиной стало то, что для студенческого хакатона мы подготовили не очень «сложные» данные небольшого объёма, поэтому современные трудоёмкие методы машинного обучения проигрывают более простым альтернативам.

Мы считаем, что это отличный урок, который поможет участникам правильно ставить задачи и выбирать оптимальные методы для их решения. Важно помнить, что сначала стоит попробовать простое решение, так называемый бейзлайн, возможно именно он позволит достичь цели в короткие сроки.

Участниками Хакатона были предложены авторские алгоритмы нахождения оптимального пути в массиве больших данных применительно к задаче автоматической сейсмической кинематической интерпретации, которая в настоящее время решается в рамках разработки корпоративного программного обеспечения в области геологии и сейсмики. Наиболее конкурентные реализации алгоритмов найдут своё применение при разработке и реализации программных модулей данных программных комплексов.

Будем рады вас видеть на финале марафона ИТ-соревнований, который пройдёт 28 ноября онлайн. В программе: награждение победителей соревнований, презентация первой версии мобильного приложения для экспресс-оценки качества пропанта. Также в рамках мероприятия будут организованы панельные дискуссии на актуальные темы «Управление данными и DS проектами» и «Компьютерное зрение». Интересными кейсами поделятся представители «Head of Data Science Alfa», CDO «Мегафон», «Huawei», «Head of CV X5» и др. Не пропустите всё самое интересное (Марафон ИТ-соревнований 2020 — Роснефть).

© Habrahabr.ru