Как рассчитать расстояние до Луны без телескопа и СМС-регистрации
В комментариях к моему прошлому посту отметили, что я не расписал, как древнегреческие астрономы высчитали расстояние до Луны. Вот этой теме и посвящен следующий текст. Правда, задача оказалась проще, чем с расстоянием до Солнца, поэтому и пост получится заметно покороче.Начну с того, что у античной науки была одна особенность: и греки (и затем римляне) фактически не умели в алгебру, они не пользовались десятичными дробями, понятием ноля, даже система счисления у тех и других была алфавитная, а не позиционная. Но зато они хорошо научились решать геометрические задачи. И познавали мир с помощью геометрии.
В частности, рассчитали расстояние до Луны. Как раз Аристарх Самосский считается первым, кому это удалось. И сделал он это следующим образом (излагаю кратко, кому нужно больше подробностей — читайте в первоисточнике, кому нужно много формул — это тоже есть в Сети, например, здесь).
Сначала он измерил угловой радиус нашего спутника. Зная его, можно рассчитать «сколько» Лун можно разместить на ее орбите. Это количество, согласно формуле длины окружности, равняется произведению радиуса орбиты (того самого расстояния) на 2 π. Теперь, для того, чтобы высчитать радиус, Аристарху нужно было рассчитать не угловой, а фактический размер Луны.
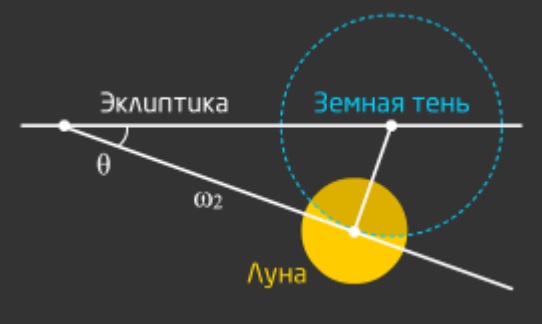
Кратко его дальнейшее решение звучало так. Затмения доказывали, что Солнце находится дальше от Земли, чем Луна, а их угловые размеры примерно равные (по расчетам Аристарха). На основании этого астроном сделал вывод, что солнечные лучи, падающие на Луну, сходятся за ней в точку на поверхности Земли. Далее он измерил тень от Земли на диске Луны во время лунного затмения. Тень получилась в два раза больше, чем сама Луна.
Аристарх суммировал результаты обоих выводов (разница в тенях и «уход» солнечных лучей от диаметра в точку) и пришел к выводу, что Луна меньше Земли в три раза. Это было довольно близко к современному ответу — в 3,6 раза.Итак, Аристарх посчитал, что Луна «укладывается» на орбиту 720 раз и она меньше Земли в 3 раза. Значит Земля «поместилась» бы на лунной орбите 240 раз. Диаметр Земли грекам был известен благодаря Эратосфену (и это было очень близкое к реальному значение). Теперь формула расчета радиуса лунной орбиты была довольно простой: 240 диаметров Земли разделить на 2 π. У Аристарха получилось 486400 км.
Спустя сто лет другой античный астроном Гиппарх уточнил его расчеты: в его ответе Луна помещалась на орбиту всего 650 раз, а расстояние получалось уже около 382 тыс. километров. Что всего на пару тысяч километров расходится с современными данными.
