Как работает неточное сравнение строк
Недавно я писал API для динамически меняющихся обоев. Обои меняются каждый день, но могут и каждые 2 часа в зависимости от обстановки в мире, например, если вышла какая-то экстраординарная новость, то показывает картинку в соответствии с данной новостью или сейчас проходит какой-то праздник, соответственно также показывает картинку с данным праздником. Если вам интересно и вы хотите помочь проекту (нужно разработать очень простые приложения для android, ios, windows, mac и т.д. все права на приложения принадлежат вам я их опубликую на сайте проекта), вот ссылка на данный проект (можете также писать в личку на этом сайте):
landing page = https://fakt309.github.io/thisisthewall
github repository = https://github.com/fakt309/thisisthewall
В моем проекте мне понадобилось сравнивать строки между собой, я поизучал как работает неточное сравнение строк и какие алгоритмы вообще существуют и готов поделиться с вами моим опытом.
Начало
В языках программирования строки сравниваются очень просто, если строка отличается хотя бы на один символ, то возвращает false.
"test" == "test" //true
"test" == "test1" //falseНо вот что если мы хотим не просто получать дискретное значение (true / false), а дифференцированное, например в процентах. Ведь согласитесь строки test и testing гораздо ближе к друг другу, чем test и abcd. Для данной проблемы существует множество решений, мы поговорим о самый популярных алгоритмах (также об их модификациях):
Расстояние Хэмминга
Расстояние Левенштейна
Сходство Джаро — Винклера
Коэффициент Сёренсена
Также сравнивать строки можно с мощью нейросетей, но в данной статье речь будет идти именно об четырёх выше перечисленных способах.
Расстояние Хэмминга
Имея множество слов, мы можем задать правило по которому будем вычислять расстояние между словами, аналогично тому как мы вычисляем в пространстве точек расстояние между точками, также мы можем задать правило по которому будем вычислять расстояние между словами. Чем больше это расстояние, тем меньше похожи слова и наоборот. Самый простой пример это расстояние Хэмминга. Данное правило работает только для слов одинаковой длины и вычисляется как число позиций отличающихся символов, пример, сравним два слова:
ромашка
монашка
В данном случае 2 позиции отличаются (первая и третья), значит расстояние 2, другой пример:
карта
каток
Здесь расстояние 3, так как 3 позиции отличаются (третья, четвёртая и пятая).
Как не трудно понять максимально расстояние между словами равно длине сравниваемых слова.
Для любой длинны и любого q-ичного алфавита мы можем получить все возможные вариации данного слова и составить метрическое пространство. Возьмем тривиальный пример с алфавитом [0, 1] и длинной слова 3. Получаем всего 8 слов: 000, 001, 010, 011, 100, 101, 110, 111. Из данных слов мы можем построить трёхмерный куб, на вершине которого будут расположены наши слова, смотри на картинке:
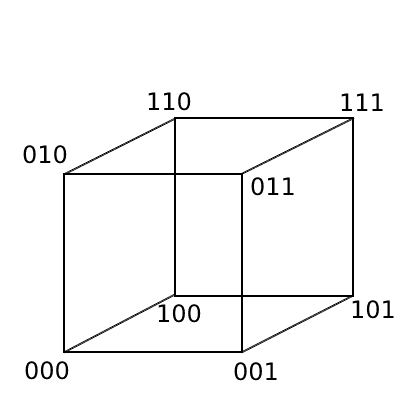
Здесь мы видим слова, которые находятся на диагонали куба имеют максимальное расстояние, например 100 и 011 (отличаются в каждой позиции) расстояние равно 3. Слова которые находятся на диагонали квадратов, имеют меньшее расстояние, например слова 000 и 101 (отличаются в двух позициях) имеют расстояние 2. И самое маленькое расстояние тех слов что находятся на одинаковых рёбрах, например 010 и 110 имеют расстояние 1 (отличаются в одной позиции). В данной метрике выполняются все необходимые аксиомы (тожества, симметрии, неравенство треугольника) так что это полноценное метрическое пространство.
Недостатки расстояния Хэмминга:
Преимущества расстояния Хэмминга:
Расстояние Левенштейна
Совершенно другой способ задания метрического пространства слов. Принцип остаётся тот же: чем больше расстояние, тем меньше похоже слова друг на друга. Но нахождение расстояния совершенно другое. Здесь мы вводим понятие односимвольной операции (их всего три):
вставка — добавляем новый символ (сыто > сытно)
удаление — удаляем символ (гидрант > гидрат)
замена — заменяем символ (усвоить > освоить)
Имея данные односимвольные операции мы можем преобразовать одно слово в другое. Расстояние по Левенштейну между двумя словами определяется как минимальное количество односимвольных операций, необходимых для преобразования из одного слова в другое. Пример:
удачливый
удачный
В данном примере было удалено 2 символа (л и и) и один символ заменён (в на н), всего три операции, значит расстояние равно 3.
Также каждой операции можно задавать свою цену, в прошлом примере цена каждой операции равнялась 1 и поэтому длина равна трём, если мы примем что замена равняется 0.5, вставка 0.7, а удаление 0.3, то получим уже расстояние в примере выше равное 1.1. Также цена операции может зависеть от символа, к которому применяется, например если мы удаляем символ а, то это одна цена, если удаляем символ б, уже другая цена, установка цен каждой операции делается вручную, если она необходима.
Недостатки расстояния Левенштейна:
Трудно находить минимальное число односимволных операций (но есть Алгоритм Вагнера-Фишера)
При перестановки слов показывает большие расстояния (например в словах хороший день — день хороший)
Расстояния между короткими, но совершенно разными словами — небольшие, в то время как между длинными строками, но похожими — большие (например кот — для маленькое расстояние, в то время как: я пришёл к себе домой — я пришел домой к себе большое расстояние)
Преимущества расстояния Левенштейна:
Работает для разных длин строк
Относительно не сложный в понимании способ (но сложный в вычислении)
Расстояние Дамерау — Левенштейна
Работает точно также как и расстояние Левенштейна, но здесь добавлена четвёртая односимвольная операция, которая называется транспозиция — замена местами двух символов (например актер — катер). Это частично решает проблему больших расстояний при перестановки слов, но усложняет алгоритм нахождения минимального числа операций.
Расстояние Джаро
Данный метод гораздо проще будет объяснить на конкретном примере. Давайте рассмотрим два слова: создание — обедать
Для начала мы посчитаем количество точных совпадений (то есть совпадает значение и порядковый номер буквы) и запишем в переменную e
создание
обедать
У нас получилось e = 2
Далее мы вычисляем длину совпадений, назовем ее l (позже вы увидите для чего она нужна) по формуле: floor( max( str1.length, str2.length ) / 2 ) - 1
У нас получается : floor ( max ( 8, 7 ) ) - 1 = floor( 8 / 2 ) - 1 = floor ( 4 ) - 1 = 4 - 1 = 3, итого l = 3
Теперь мы находим количество неточных совпадений, назовём ее z данное количество вычисляется следующим образом берём: каждую n-ую букву первого слова и сверяем с каждой буквой n ± l, но не с точным совпадением, пример показан ниже на картинке:

Как видно из картинки например буква а пятая по счёту, значит сравниваю данную букву со всеми буквами второго слова 5 ± 3, кроме пятой буквы (то есть 2, 3, 4, 6, 7, 8) и так проделываем со всеми буквами первого слова, получаем количество неточных совпадений. В моем случае получилось z = 1
Теперь обозначим новые переменные как m = e + zи t = z / 2
И в итоге формула расстояния Джаро будет выглядеть так:
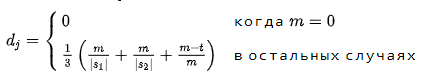
Здесь |s1| , |s2| — длины первой и второй строки
В моем случае:
m = 2 + 1 = 3
t = 1 / 2 = 0.5
d = (1 / 3) * ( 3 / 8 + 3 / 7 + (3 - 0.5) / 3 ) ≈ 0.33 * ( 0.36 + 0.43 + 0.83 ) ≈ 0.53
Наше расстояние получилось 0.53
Ответ всегда должен получаться от 0 до 1, где 0 — точное совпадение слов, 1 — полное не совпадение слов.
Преимущества расстояния Джаро:
Работает с разной длинной строк
Довольно точно считает на практике
Выдает нормированный результат (то есть от 0 до 1)
Сходство Джаро — Винклера
Самый эффективный метод (на мой взгляд), который я лично использовал в своём проекте. Работает по такому принципу: сначала мы находим расстояние Джаро, затем задаем коэффициент масштабирования p (по стандарту рекомендуется 0.1, можно менять, но оно не должно превышать 0.25) и находим расстояние Джаро — Винклера следующим образом:
Сначала считаем длину совпадающего префикса и записываем в переменную l (это количество первых совпадающих символов) например в словах комитет — комиссия количество первых букв совпадающих равняется 3, а в словах нить — натрий l = 1
Пусть d -расстояние Джаро между словами s1 и s2, p — коэффициент масштабирования, l — длинна совпадающего префикса, тогда формула Джаро — Винклера выглядит следующим образом:
j = d + (l * p ( 1 - d ))
Преимущества расстояния Джаро — Винклера:
Даёт бонусную надбавку словам с одинаковыми префиксами, что зачастую повышает точность вычисления схожести по сравнению с расстоянием Джаро
Недостатки расстояния Джаро — Винклера:
Не явлется метрикой в математическом понимании так как не выполняется правило треугольника, соответственно все теоремы, аксиомы для метрики не применимы и трудно рассматривать как математическую модель, но на практике работает не плохо.
Коэффициент Сёренсена
Коэффициент Сёрнсена придуман для определения схожести любых множеств. В случае со словами его также удаётся применить.
Представим у нас есть два множества A = [a, b, c] и B = [b, c, d, e] вычислим коэфициент Сёренсена для данных множеств по формуле:
K = 2 * |A∩B| / (|A| + |B|)
где A∩B — пересечение множеств, |A| — мощность множества (количество элементов в конечном множестве)
В нашем случае
A∩B = [b, c]
|A∩B| = 2
|A| = 3
|B| = 4
Получаем K = 2 * 2 / (3 + 4) = 4 / 7 = 0.57
Теперь как мы это применим к словам. Слова мы можем представить как множества, например возьмем два слова: звено — зерно
Первое слово можем представить как множество [з, в, е, н, о]
Второе слово можем представить как множество [з, е, р, н, о]
Но здесь есть проблема: в множествах отсутствует порядок, и таким образом если мы будем считать коэффициент Сёренсена для данных множеств, то при перестановки букв местами коэффициент не будет меняться совсем, поэтому есть решение, представлять слово в виде множества биграмм, то есть последовательности из двух букв, смотрите на примере.
Слово звено превращаем в множество биграмм: [зв, ве, ен, но]
Слово зерно превращаем в множество биграмм: [зе, ер, рн, но]
Здесь как мы видим каждый элемент множества состоит из последовательности двух букв идущих по порядку в слове. Теперь просто для данных множеств считаем коэффициент Сёренсена как мы делали выше
K = 2 * 1 / (4 + 4) = 2 / 8 = 0.25
Данный метод довольно экзотический и я редко сталкивался с ним на практике как метод расчёта схожести строк.
Итог
На мой взгляд самый лучший метод расчёта Сходство Джаро — Винклера или же просто расстояние Джаро, выдает самые лучшие результаты относительно не сложные алгоритмы вычисления плюс нормированный результат, который можно переводить в проценты. Также имеет смысл рассматривать расстояние Левенштейна (или Дамерау — Левенштейна), но только если грамотно вручную установить каждой операции цену, тогда это может работать, но я так и не смог это осилить. Растояние Хэмминга работает неплохо и максимально простое, но большой минус что работает только для одинаковых длин строк, может подойти в генетике, где сравниваются гены равной длинны.
Если кому интересен проект, присоединяйтесь мне нужно написать приложения которые берут картинку по ссылке из api и устанавливают на рабочий стол каждые 2 часа, по сути приложение очень простое, если кто умеет, буду благодарен (android, ios, windows, macOS, расширение для chrome кто что умеет делать, ваши работы выложу на своем сайте).
landing page = https://fakt309.github.io/thisisthewall
github repository = https://github.com/fakt309/thisisthewall
