Как перестать гадать и начать считать
Трафик, из всех физических явлений, является достаточно сложным с точки зрения природы процесса, так как, насколько мне известно, еще никто не сформулировал математические законы, описывающие трафик. Тем не менее, попробуем применить элементарные методы теории вероятности и математической статистики для формализации и оценки правдоподобия наших суждений.
Не стыдно ль физику, то есть исследователю и испытателю природы, искать свидетельства истины в душах, порабощенных обычаем? Марк Туллий Цицерон, более 2000 лет назад
Истина часто остается принципиально недостижимой. Проводя исследования, мы все равно сталкиваемся с вопросами, на которые нельзя дать однозначный и достоверный ответ.
Но так ли это плохо?
Лишаясь возможности утверждать, мы всегда оставляем за собой право оценивать. Эта лазейка пусть и не позволяет нам коснуться истины, но позволяет приблизиться к ней. Другое дело, что люди по незнанию или злому умыслу регулярно идут в другую сторону, отдаляясь от истины.
Не могу удержать себя от удовольствия на мгновение погрузиться в историю этого вопроса.
Экскурс в историю теории вероятности и математической статистики
Один из самых важнейших навыков в математике — искусство неточных вычислений.
Начало систематического исследования задач, относящихся к массовым случайным явлениям, и появление соответствующего математического аппарата относятся к XVII веку. Галилей пытался исследовать ошибки физических измерений и оценить их вероятность.
Для всего XVIII и начала XIX века характерны бурное развитие теории вероятностей и повсеместное увлечение ею. Теория вероятностей становится «модной» наукой. Ее начинают применять не только там, где это применение правомерно, но и там, где оно ничем не оправдано. Для этого периода характерны многочисленные попытки применить теорию вероятностей к изучению общественных явлений, к так называемым «моральным» или «нравственным» наукам. Появились работы, посвященные вопросам судопроизводства, истории, политики, даже богословия, в которых применялся аппарат теории вероятностей. Для всех этих псевдонаучных исследований характерен чрезвычайно упрощенный, механистический подход, к рассматриваемым в них общественным явлениям. В основу рассуждения полагаются некоторые произвольно заданные вероятности (например, при рассмотрении вопросов судопроизводства склонность каждого человека к правде или лжи оценивается некой постоянной, одинаковой для всех людей вероятностью), и далее общественная проблема решается как простая арифметическая задача. Естественно, что все подобные попытки были обречены на неудачу и не могли сыграть положительной роли в развитии науки. Напротив, их косвенным результатом оказалось то, что примерно в 20х-30х годах XIX века в Западной Европе повсеместное увлечение теорией вероятностей сменилось разочарованием и скептицизмом. На теорию вероятностей стали смотреть как на науку сомнительную, второсортную, род математического развлечения, вряд ли достойный серьезного изучения.
На это моменте стоит сделать паузу и отметить, что в то время теория вероятностей и математическая статистика выглядели совсем не так, как выглядят сейчас.
Именно в начале XIX века в России создается та знаменитая Петербургская математическая школа, трудами которой теория вероятностей была поставлена на прочную логическую и математическую основу и сделана надежным, точным и эффективным методом познания. Со времени появления этой школы развитие теории вероятностей уже теснейшим образом связано с работами русских, а в дальнейшем — советских ученых.
В качестве дани уважения я приведу их фамилии, а вы по ним можете вспомнить (если когда-либо занимались тервером и матстатом) как прочно вошли их имена в эти науки.
В.Я. Буняковский, П.Л. Чебышев, А.А. Марков, А.М. Ляпунов, а за ними С.Н. Бернштейн, А.Я. Хинчин, А.Н. Колмогоров, В.И. Романовский, Н.В. Смирнов Е.Е. Слуцкий, Б.В. Гнеденко и другие.
Итак, прежде чем вернемся к нашему вопросу, давайте я напомню об основах, без которых нам будет трудно двигаться дальше.
Краткое введение в математическую статистику
Событие — факт, который произошел или не произошел в результате опыта. Например:
- При броске кубика выпало 5 очков.
- Пользователь зашел на сайт.
Случайная величина — величина, которая в результате опыта принимает значение, которое было неизвестно заранее. Например:
- Количество очков, выпавших на кубике.
- Сумма всех очков, выпавших на кубике за 1000 бросков.
- Количество просмотров страниц на сайте в течении дня.
Возьмем опыт с бросанием обычного шестигранного кубика: событие случайно и мы не можем предсказать его результат, то есть заранее назвать выпавшую грань.
Математические законы теории вероятности получены абстрагированием реальных статистических закономерностей, свойственных массовым случайным явлениям. Наличие этих закономерностей связано именно с массовостью явлений, то есть с большим числом выполняемых однородных опытов.
Конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате массы таких явлений: случайные отклонения от среднего взаимно нивелируются. Именно эта устойчивость средних и представляет собой физическое содержание закона больших чисел: при очень большом числе случайных явлений средний их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности.
Таким образом даже для абсолютно случайных событий, существуют «устойчивые» метрики. В предыдущем примере мы можем оценить сколько очков в среднем будет выпадать на шестигранном кубике при большом количестве испытаний. Для этого мы бросим кубик много раз просуммируем все выпавшие очки и разделим на количество испытаний.
Таким же образом, зная историю посещений на сайте, мы можем с хорошей точностью предсказать посещаемость в какой-то определенный день.
Примерение методов математической статистики в веб-аналитике
Возьмем открытую статистику просмотров с liveinternet для сайта XXX
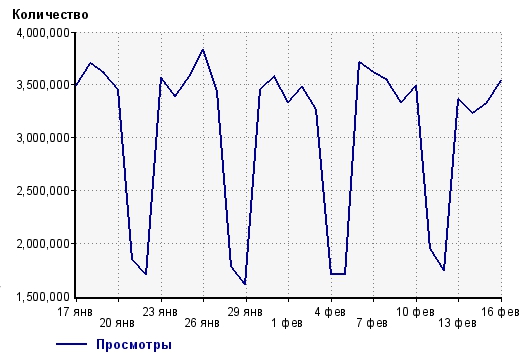
Вопрос: насколько «большим» должно быть изменение на сайте/в маркетинге, чтобы мы могли однозначно (вернее, с большой степенью вероятности) утверждать, что это изменение повлияло на текущую метрику?
Перенесем данные в таблицу.
Текущий статистический материал представляет собой простой статистический ряд. Каждый элемент ряда — выборка случайных величин, достаточно большого объема, чтобы в ней были выявлены существенные черты излучаемого распределения. В пользу этого нам говорит тот факт, что на графике можно увидеть некую периодическую закономерность.
Мы не ставим себе цель решить задачу о выравнивании статистических рядов (то есть задачу поиска теоретической кривой распределения, выражающую черты стат. материала), так как поиск аналитического представления полученных данных — задача сама по себе неопределенная и решается, в первую очередь, из соображений физики процесса. Увы, природа трафика настолько сложна, что у нас нет возможности описать его теоретически.
Более того, чтобы найти закон распределения, нужен обширный стат. материал, порядка нескольких сотен наблюдений. Увы, мы таким не обладаем, но тем не менее, мы можем ориентировочно определить важнейшие числовые характеристики случайной величины: математическое ожидание, дисперсию и среднеквадратическое отклонение.
Сделаем некоторый вывод о физике процесса:
Трафик имеет цикличную природу, поэтому некорректно сравнивать разные дни недели между собой. То есть, если мы хотим узнать как ведет себя трафик в понедельник и насколько он аномален — мы должны сравнивать текущий понедельник со всеми предыдущими понедельниками. Или брать больший период для исследований, например неделю, чтобы избавиться от периодической зависимости.
В таблице, что я привел выше, возьмем 5 последних сред (то есть данные по просмотрам за 18 января, 25 января, 1 февраля, 8 февраля и 15 февраля).
Оценим для выборки этих дней математическое ожидание и дисперсию. Известно что статистическое среднее случайной величины стремиться к мат. ожиданию при количестве опытов, стремящихся к бесконечности. Увы, на практике у нас редко будет большое количество опытов, поэтому мы принимаем во внимание тот факт, что наше математическое ожидание посчитано неточно.
Дана выборка из пяти элементов:
3 703 900
3 577 305
3 329 611
3 538 719
3 325 899
Мат. ожидание (оно же статистическое среднее): 3 495 087
Несмещенная дисперсия: 27 068 326 459
Стандартное отклонение (квадратный корень из дисперсии): 164 525
Теперь самое интересное. Существует одна такая штука, называется неравенство Чебышева. Если коротко, оно утверждает что случайная величина в основном принимает значение, близкое к своему среднему. Это же неравенство дает численную оценку этому событию:
Случайная величина с вероятностью
Что это значит? Возьмем k=2 для нашей выборки.
Получаем, что случайная величина попадет в интервал (3 166 037, 3 824 137) с вероятностью 75%.
Чаще всего берут k=3 стандартных отклонения (знаменитое правило трех сигм), так как в худшем случае точность составляет 88%.
Такая точность соответствует интервалу (3 001 512, 3 988 662).
Образованной читатель может отметить, что правило трех сигм дает большую точность в некоторых случаях. Да, это так, в некоторых случаях точность оценки можно усилить, но для этого нужно знать чуточку больше о характере распределения, и в данной статье мы себе не ставим такую задачу.
Выводы
Прежде чем сделать какие-то выводы, давайте графически изобразим наши результаты:
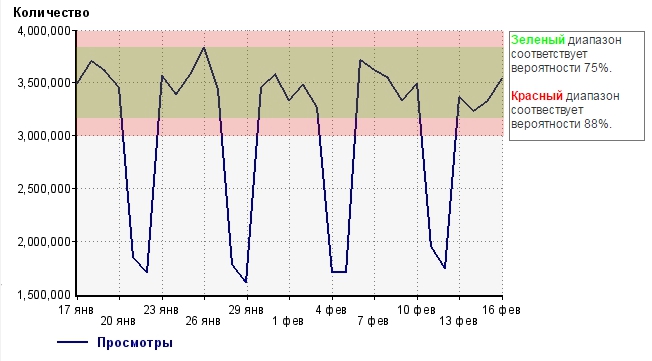
Мы выяснили, что наша случайная величина (сумма просмотров сайта в течении дня) с вероятностью 75% попадет в зеленый диапазон, и с вероятностью 88% попадет в красный диапазон, в случае, если мы ничего не будем кардинально менять в природе возникновения этой величины, то есть менять интерфейс на сайте или проявлять маркетинговую активность.
Итак, что нам это дает? Для начала выберем границу, которой мы будем «верить». Традиционно возьмем интервал в 3 сигма, то есть красного цвета.
Он дает окно, которое отклоняется от среднего на 14,1%.
Если мы проведем какой-нибудь эксперимент, например проведем A/B-тест и в следующую среду (22 февраля) замерим результат, то можем сделать следующие выводы:
1. Если результат эксперимента изменил наш показатель более чем на 14,1% — скорее всего эксперимент успешный.
2. Если результат эксперимента изменил наш показатель менее чем на 14,1% — эксперимент не может быть достоверным, так как возможный эффект находится в пределах статистической погрешности и «смазывается» ею. То есть, даже если положительный эффект был — мы не можем это достоверно доказать при текущей оценке.
Что же делать? Улучшать оценку (брать большее количество наблюдений, а не 5, как делал я), таким образом растягивая длительность эксперимента.
Спасибо за прочтение. Буду рад критике, предложениям и уточнениям.
Список публикаций, использованных в посте:
- Е.С. Вентцель «Теория Вероятностей» (1969 год, очень забавная книжка, каждая вторая задача про военное дело. Видимо сказывается отпечаток холодной войны :)
- В.В. Светозаров «Элементарная обработка результатов измерений»
Комментарии (8)
19 февраля 2017 в 16:02
0↑
↓
Автор, можно ведт взять и провести этот эксперимент, указанный в конце статьи, задним числом. Взять сайт, построить график. Взять какую-то их рекламную компнию или акцию или новости или редизайн и посмотреть, как это влияло на посещаемость. Или я чего-то не понял?
19 февраля 2017 в 16:05
0↑
↓
Вопрос в том, как убедиться, повлияло ли изменение на метрику. В посте я пытаюсь доказать, что любое изменение, которое меняет метрику менее чем x% (в примере это 14), нельзя точно приписать к вашему эксперименту — это может быть влияние случайности.
19 февраля 2017 в 16:05
+1↑
↓
Очень важно в таких расчётах помнить о стационарности — то есть постоянстве внешних условий.19 февраля 2017 в 18:43
0↑
↓
Это вопрос, который портит всю малину.
И второй такой же вопрос, в контексте подобной аналитики — как убедиться, что выборка Б, «такая же», как и выборка А (т.е. обе выборки принадлежат одной и той же генеральной).
19 февраля 2017 в 16:12
0↑
↓
Ответ на вопрос из спойлера — 10,5. Можно конечно все 6^3 вариантов перебрать. Но разницы нет, сразу мы 3 кубика бросаем, или по 1, но 3 раза.19 февраля 2017 в 16:12
0↑
↓
да ;)
19 февраля 2017 в 16:12
0↑
↓
Трафик, из всех физических явлений, является достаточно сложным с точки зрения природы процесса, так как, насколько мне известно, еще никто не сформулировал математические законы, описывающие трафик
Агнер Эрланг перевернулся в гробу19 февраля 2017 в 16:21
0↑
↓
Мне почему-то в голову не пришло рассматривать трафик и показатели на его основе в качестве потоков из теории массового обслуживания. Я это связываю вот с тем, что я не знаю теории массового обслуживания и то, как она работает и на какие вопросы отвечает. Но, полагаю, что там совершенно про другие задачи.Буду рад ошибаться, и если вы поделитесь какой-нибудь близкой работой с применением ТМО, желательно из области веб-аналитики… это было бы чудесно!
