Как нарисовать звезду (и не только) в полярных координатах22.09.2020 08:48

Вопрос о формуле для многоугольника в полярных координатах регулярно возникает на тематических ресурсах — и так же регулярно остаётся без внятного ответа. В лучшем случае попадается решение через функцию остатка от деления — что не является «чистым» с математической точки зрения, поскольку не позволяет производить над функцией аналитические преобразования. Видимо, настоящие математики слишком заняты решением проблем тысячелетия и поисками простого доказательства теоремы Ферма, чтобы обращать внимание на подобные банальные задачи. К счастью, в этом вопросе воображение важнее знания, и для решения этой задачи не нужно быть профессором топологических наук — достаточно знания школьного уровня.

Формула для равностороннего многоугольника в полярных координатах выглядит очень просто

$\rho = \frac{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}(k \cos (n \phi ))+\pi m}{2 n}\right)}$

и имеет следующие параметры:

$\phi$ — угол;
$n$ — количество выпуклых вершин;
$m$ — определяет, через какое количество вершин стороны будут лежать на одной прямой. Для него допустимы и отрицательные значения — от знака будет зависеть, в какую сторону будет выгибаться звезда;
$k$ — жёсткость — при $k=0$ мы получим окружность вне зависимости от прочих параметров, при $ k=1$ — многоугольник с прямыми линиями, при промежуточных значениях от $0$ до $1$ — промежуточные фигуры между окружностью и многоугольником.

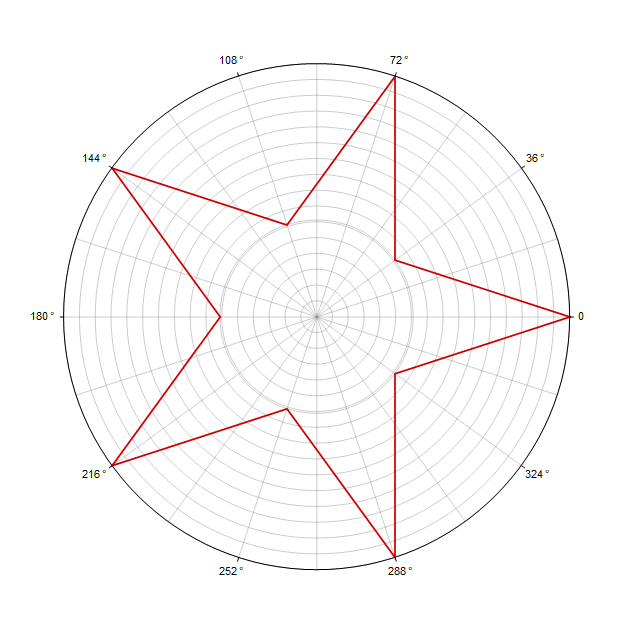
С этой формулой можно нарисовать звезду двумя путями:

1) $n=5, m=3$

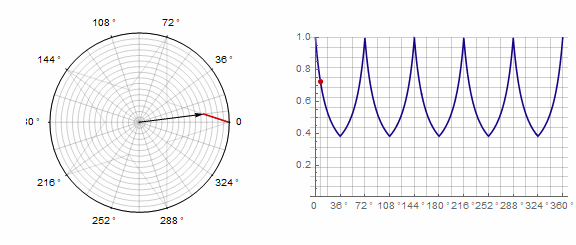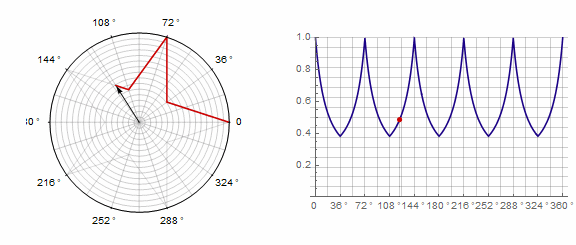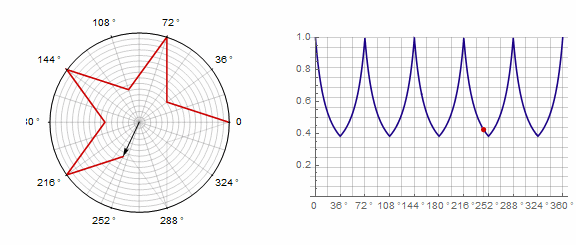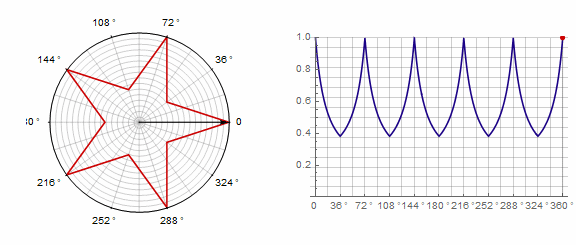
2) $n=5/4,m=0$ . В этом случае требуется сделать два оборота вместо одного:

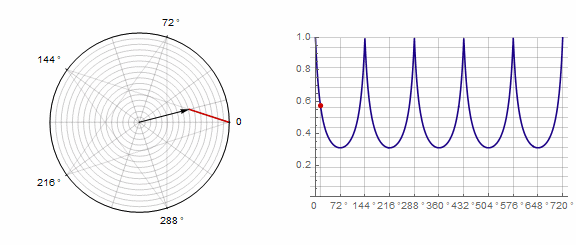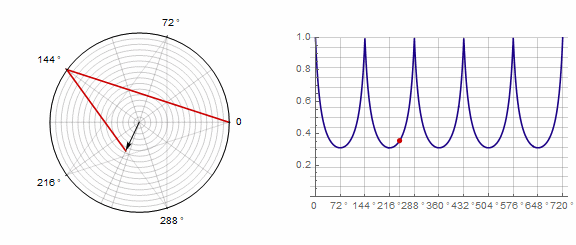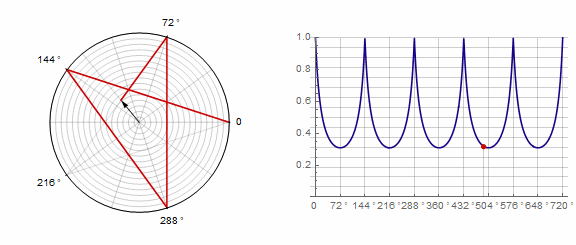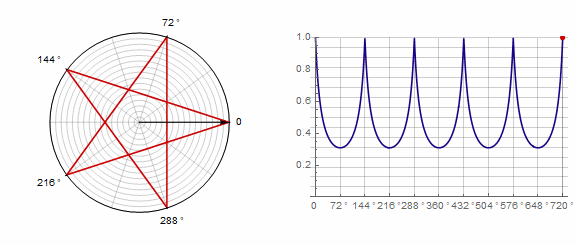
Параметр $m$ влияет на многоугольник следующим образом (здесь он изменяется от -1 до 5):

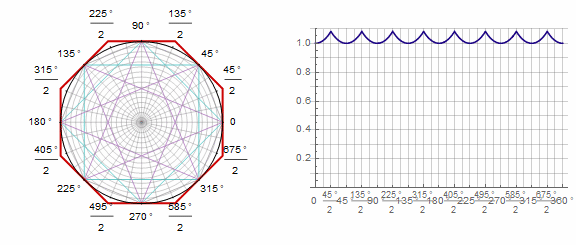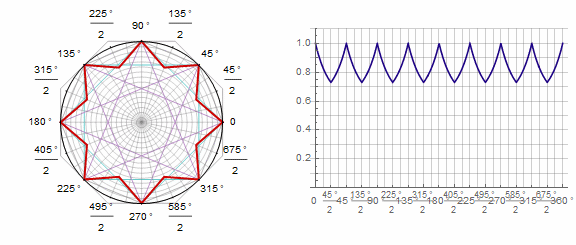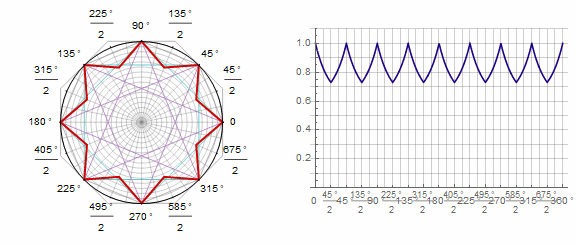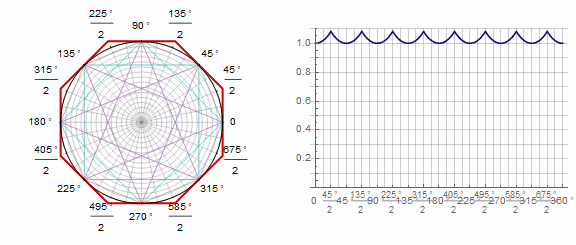
Параметр $k$ в анимации:

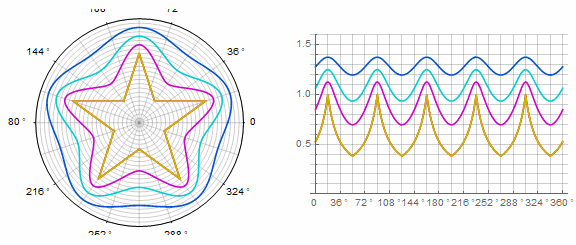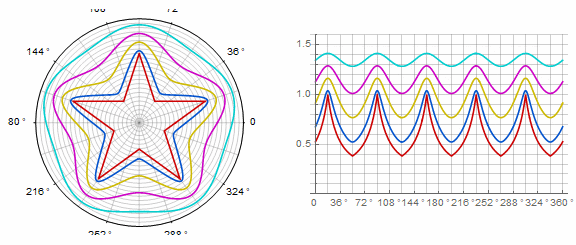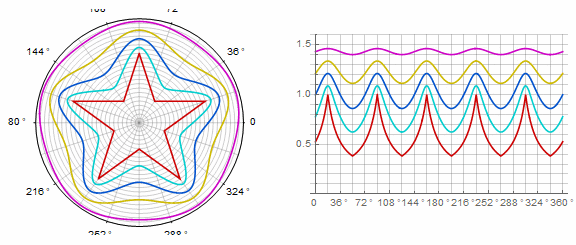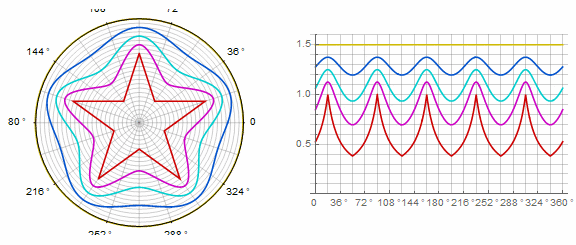
Комплексная форма и модификации

Можно переписать исходную формулу в комплексном виде, и, несмотря на наличие в ней мнимых единиц, значение радиуса по-прежнему будет оставаться действительным:

$\small\rho = \frac{4^{1/n} \left(\sqrt{1-k^2}+i k\right)^{-1/n} \left(1+\left(\sqrt{1-k^2}+i k\right)^{2/n} e^{\frac{i \pi m}{n}}\right) \left(\sqrt{1-k^2 \cos ^2(n \phi )}+i k \cos (n \phi )\right)^{1/n}}{4^{1/n}+e^{\frac{i \pi m}{n}} \left(2 \sqrt{1-k^2 \cos ^2(n \phi )}+2 i k \cos (n \phi )\right)^{2/n}}$

На первый взгляд это может показаться бессмысленным, поскольку формула стала чуть более громоздкой —, но не стоит спешить с выводами. Во-первых, в ней отсутствует арксинус, что полностью меняет математический смысл формулы и позволяет по-другому посмотреть на построение звёздчатого многоугольника. Во-вторых, из неё также можно получить компактные формулы для частных случаев, например $\frac{i^t \left(i^{n t}\right)^{1/n}}{1+\left(i^{n t}\right)^{2/n}}$ . В-третьих (и самое интересное), её можно творчески модифицировать и получать другие, неожиданные формы. Для того, чтобы появление возможной мнимой компоненты в радиусе не вызывало неоднозначности при вычислении, можно её сразу привести к декартовым координатам умножением на $e^{i \phi }$ . Вот примеры некоторых модификаций:

$\frac{(-1)^{2/3} e^{i \phi } \sqrt[3]{\sqrt{\sin ^2(3 \phi )}+i \cos (3 \phi )}}{(-1)^{2/3}+2^{2/3} \left(\sqrt{\sin ^2(3 \phi )}+i \cos (3 \phi )\right)^{2/3}}$

$\frac{e^{i \phi } \sqrt{\sqrt{\sin ^2(2 \phi )}+i \cos (2 \phi )}}{\sqrt{2} \left(\sqrt{\sin ^2(2 \phi )}+i \cos (2 \phi )\right)^{3/2}+e^{i/2}}$

$\frac{e^{\frac{1}{4} i (4 \phi +\pi )}}{2 \sqrt{\sqrt{\sin ^2(2 \phi )}+\sqrt[4]{-1} \cos (2 \phi )}+(-1-i)}$

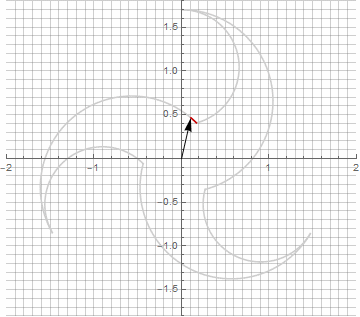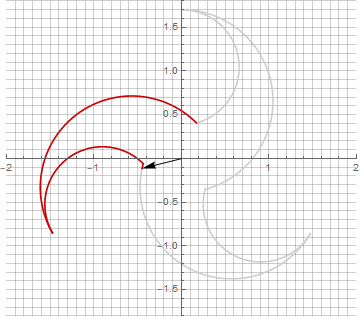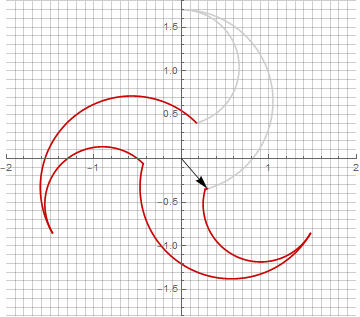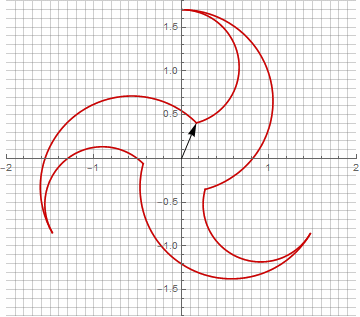
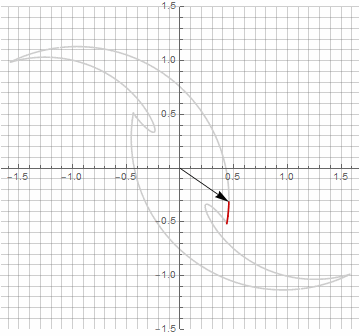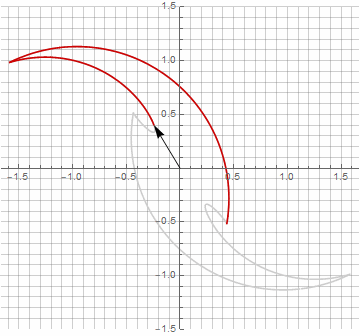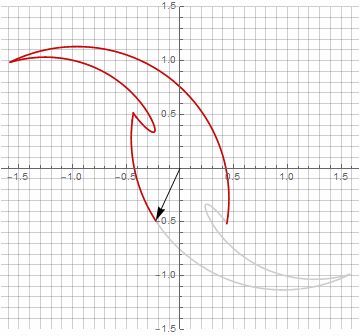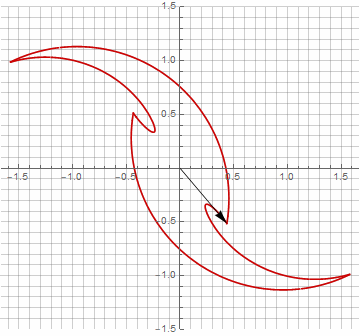
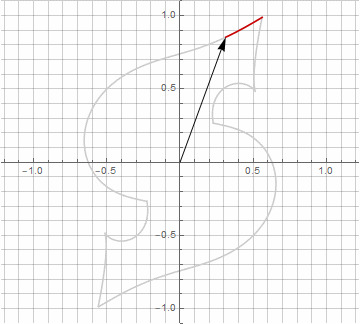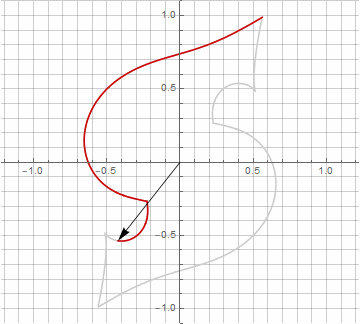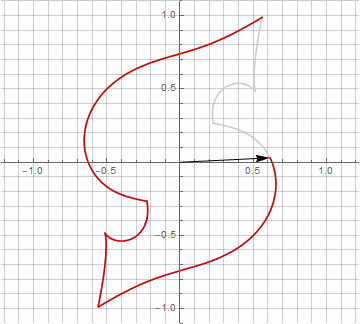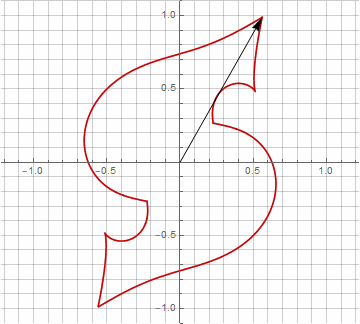
Как вы наверняка заметили, вращение вектора перестало быть равномерным — и именно из-за появления мнимой составляющей в радиусе.

Квадрокруги и прочее

У нашей формулы есть замечательный частный случай — квадрат, формулу для которого можно выписать как

$\rho = \frac{2}{\sqrt{2+\sqrt{2+2 \cos (4 \phi )}}}$

или

$\rho = \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 \phi )}}}$

(выбирайте, какая больше нравится).

В чуть более развёрнутом случае можно определить промежуточные фигуры между кругом и квадратом через точку $(k,k)$ на плоскости

$\rho = \sqrt{\frac{2}{1+\sqrt{1-\frac{\left(2 k^2-1\right) \sin ^2(2 \phi )}{k^4}}}}$

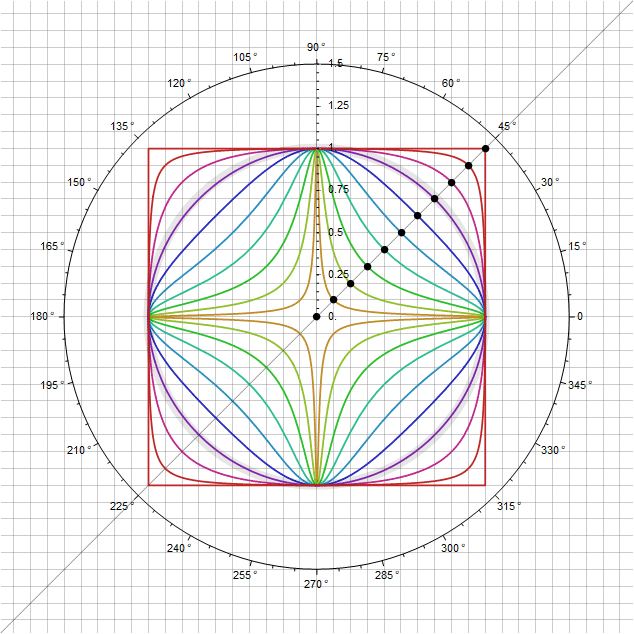
Можно также добавить вариативности этим фигурам с сохранением условия прохождения их через точку $(k,k)$ — модулируя непосредственно сам параметр $k$ в зависимости от угла таким образом, чтобы при прохождении через диагонали его множитель был равен единице. Например, подставив вместо $k$ функцию $\frac{k}{1-z \cos ^2(2 \phi )}$ , мы получим дополнительный параметр $z$ , которым можно регулировать дополнительные изгибы. В частности, для $z=1/4$ получится следующее:

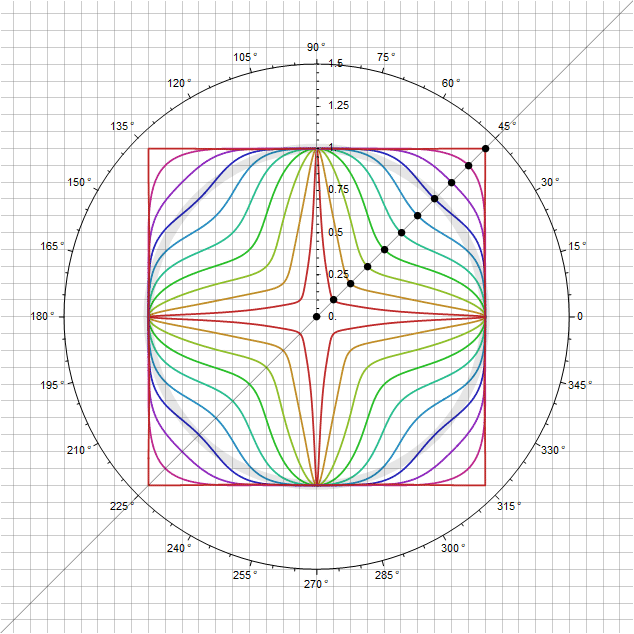
В ещё более развёрнутом случае можно определить не просто квадрат —, а прямоугольник, и по прежнему в полярных координатах:

$\rho = \sqrt{\frac{4 a^2 b^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right) \left(\sqrt{1-\frac{4 a^2 b^2 k \sin ^2(2 \phi )}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right)^2}}+1\right)}}$

И даже посчитать его площадь (через эллиптические интегралы):

$S=4 a b\frac{((k-1) K(k)+E(k))}{k}$

Примечание

Это позволит делать профили с переходом из окружности в прямоугольник с контролируемой площадью сечения. Здесь площадь константна:

А здесь площадь расширяется по экспоненциальному закону:

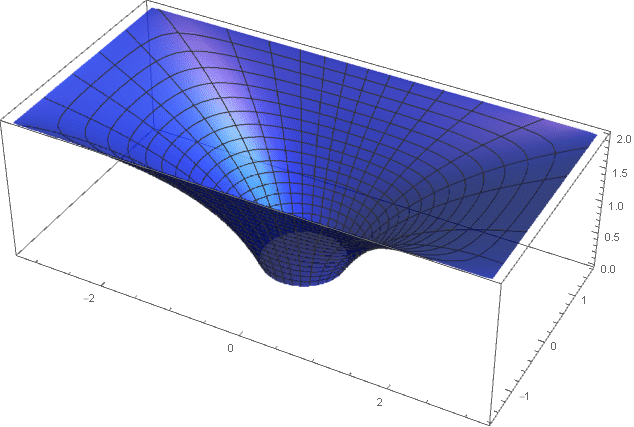
Переход к декартовым координатам

Любую формулу в полярных координатах можно выразить через уравнение в декартовых координатах, причём как минимум двумя способами — в зависимости от чего будет изменяться вид градиента на границе фигуры. Для этого достаточно посчитать угол через арктангенс от координат и привести формулу к константе через радиус-вектор вычитанием

$0=\sqrt{x^2+y^2}-\frac{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}\left(k \cos \left(n \tan ^{-1}(x,y)\right)\right)+\pi m}{2 n}\right)}$

или делением

$1=\frac{\sqrt{x^2+y^2} \cos \left(\frac{2 \sin ^{-1}\left(k \cos \left(n \tan ^{-1}(x,y)\right)\right)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}$

Второй вариант предпочтительнее, поскольку даёт прямые градиенты вдоль сторон многоугольника.

Примечание

Здесь также нужно помнить, что в точке (0,0) возникает неопределенность из-за деления на ноль — которая, впрочем, легко разрешается через предел (который будет равным $-\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right) \sec \left(\frac{2 \sin ^{-1}\left(k \cos \left(\frac{\pi n}{2}\right)\right)+\pi m}{2 n}\right)$ в первом случае и нулю во втором).

Выражение $\cos \left(n \tan ^{-1}(x,y)\right)$ также можно упростить до $\frac{(x+i y)^n+(x-i y)^n}{2 \left(x^2+y^2\right)^{n/2}}$ , коэффициенты числителя которого при разложении образуют знакочередующий вариант последовательности A034839.

Значение формулы из правой части уравнения (во 2-м случае) будет меняться от $0$ до $1$ если точка $(x,y)$ попадает внутрь фигуры, и от $1$ до бесконечности — если нет. Выбирая различные функции для преобразования её в яркость, можно получать различные варианты растеризации. Для экспоненты ( $e^{-x-1}$ для первого и $e^{-x}$ для второго варианта) получим
или, если с насыщением
Можно использовать классический фильтр нижних частот $\frac{1}{x^p+1}$ , в котором $p$ — порядок фильтра, определяющий степень затухания.

Для первого варианта:

И для второго:
Можно использовать и кусочно-непрерывную функцию, явно задавая границы интерполяции.

Помимо растеризации как таковой, можно задавать и деформации — например, сжать шахматную доску в круг:

Или даже натянуть её на сферу:

формула

Appendix: как была получена формула

Классический стиль повествования в математических текстах состоит из чередования лемм/теорем и их доказательств — как если бы доказуемые утверждения появлялись у авторов в голове откровением свыше. И хотя в этом и бывает доля истины, чаще появлению формул предшествует некоторая исследовательская работа, описание которой может дать большее понимание их смысла, чем формальное доказательство;, а верность утверждений, в свою очередь, можно проследить через верность шагов, к ним приведших.

Так и здесь — если бы статья началась с формулы в комплексной форме, то её появление было бы неочевидным и контр-интуитивным, а заявленные свойства требовали бы дополнительных доказательств. Но в тригонометрической форме записи историю её появления вполне возможно проследить.

1) начинаем с самого простого случая — задаче начертить прямую в полярных координатах. Для этого нужно решить уравнение $r \cos (\phi )=1$ , решение которого очевидно $r\to \sec (\phi )$ .

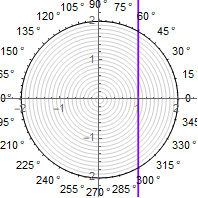
2) далее аргумент секанса нужно «зациклить», чтобы обеспечить изломы в прямой. Именно на этом этапе другие решения используют «грязный хак» в виде остатка от деления. Здесь же используется последовательное взятие прямой и обратной функции синуса — $\sin ^{-1}(\sin (\phi ))$

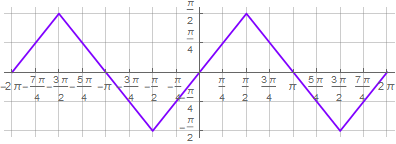
Такой подход позволяет производить стандартные математические операции над получившейся формулой,

например

можно её продифференцировать и получить функцию для прямоугольной волны:

$\frac{\partial \sin ^{-1}(\sin (\phi ))}{\partial \phi }=\frac{\cos (\phi )}{\sqrt{1-\sin ^2(\phi )}}$

Благодаря этой же записи можно упростить функцию квадрата в полярных координатах до более эстетического вида, используя представление тригонометрический функций в комплексном виде. В Wolfram Mathematica это можно сделать с помощью функций TrigToExp и ExpToTrig:

код

Sec[1/2 ArcSin[k Sin[2 \[Phi]]]]^2//TrigToExp//ExpToTrig//Sqrt[#]&//FullSimplify
↓

$\frac{2}{\sqrt{2+2 \sqrt{1-k^2 \sin ^2(2 \phi )}}}$

Благодаря этой же записи можно получить гладкие промежуточные фигуры между кругом и квадратом с помощью дополнительного множителя $k$ , благодаря которому аргумент арксинуса не дотягивает до единицы — $\sin ^{-1}(k \sin (\phi ))$ :

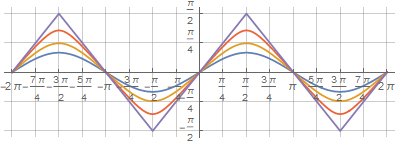
А для того, чтобы функция пересекала заданную точку, нужно просто составить уравнение и пересчитать $k$ :

$\sqrt{\frac{2}{1+\sqrt{1-k' \sin ^2( \frac{\pi}{2} )}}}=k$

код

Solve[(Sqrt[2/(1+Sqrt[1-k Sin[2 \[Phi]]^2])] /. \[Phi]->Pi/4)==x, k] /. x->k
↓

$k'\to \frac{4 \left(k^2-1\right)}{k^4}$

3) параметры $n$ и $m$ были просто добавлены творческим способом и их влияние исследовалось экспериментально, по факту.

4) Прямоугольник легко получить перейдя к параметрическому виду и «растягиванием» осей

$x=a \cos (t) \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 t)}}}$

$y=b \sin (t) \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 t)}}}$

Но после этого $t$ уже не будет значить угол, теперь $t$ — это просто параметр, который описывает вектор через его проекции на координатные оси. Чтобы перейти обратно к полярным координатам нужно найти длину вектора (через корень суммы квадратов), угол (через арктангенс отношения), выразить этот угол через $\phi$ и подставить получившееся выражение вместо $t$ .

код

With[{r = Sqrt[2/(1 + Sqrt[
1 - Sin[2 t]^2])]}, {Sqrt[(a r Cos[t])^2 + (b r Sin[t])^2], 
ArcTan[(b r Sin[t])/(a r Cos[t])]}] // Simplify

↓

$\left\{\sqrt{2} \sqrt{\frac{a^2 \cos ^2(t)+b^2 \sin ^2(t)}{\sqrt{\cos ^2(2 t)}+1}},\tan ^{-1}\left(\frac{b \tan (t)}{a}\right)\right\}$

Solve[ArcTan[(b Tan[t])/a]==\[Phi], t]
↓

$t\to \tan ^{-1}\left(\frac{a \tan (\phi )}{b}\right)$

Sqrt[2] Sqrt[(a^2 Cos[t]^2 + b^2 Sin[t]^2)/(1 + Sqrt[Cos[2 t]^2])] /. t -> ArcTan[(a Tan[\[Phi]])/b] // Simplify
↓

$\sqrt{2} \sqrt{\frac{a^2 b^2 \sec ^2(\phi )}{\left(a^2 \tan ^2(\phi )+b^2\right) \left(\sqrt{\cos ^2\left(2 \tan ^{-1}\left(\frac{a \tan (\phi )}{b}\right)\right)}+1\right)}}$

Упростить такую формулу уже посложнее, и для этого потребуется несколько этапов:

1) перейти к декартовым координатам заменой $\phi \to \tan ^{-1}(x,y)$ ;
2) перейти к экспоненциальному виду;
3) упростить;
4) сделать обратную замену $x\to \cos (\phi )$ и $y\to \sin (\phi )$ ;
5) опять перейти к экспоненциальному виду;
6) упростить.

В результате получим такую формулу:

код

Sqrt[2] Sqrt[(a^2 b^2 Sec[\[Phi]]^2) / ((1 + Sqrt[Cos[2 ArcTan[(a Tan[\[Phi]])/b]]^2]) (b^2 + a^2 Tan[\[Phi]]^2))] /. \[Phi] -> ArcTan[x, y] // TrigToExp // Simplify // # /. {x -> Cos[\[Phi]], y -> Sin[\[Phi]]} & // TrigToExp // Simplify // FullSimplify
↓

$2 \sqrt{\frac{a^2 b^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right) \left(1+\sqrt{\frac{\left(\left(a^2+b^2\right) \cos (2 \phi )-a^2+b^2\right)^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right)^2}}\right)}}$

Заключение

Как видите, даже в такой простой и банальной вещи как многоугольник, можно найти и придумать что-то новое. И на этом история не заканчивается — осталась неизвестной формула площади для общего случая, осталась неизвестной формула для произвольного, а не только правильного многоугольника, остались без рассмотрения разложения в степенные и тригонометрические ряды. Также, вероятно, подобного рода формула существует и для 3-мерного случая.

Поэтому если вам говорят, что в математике уже всё придумано и остались лишь задачи недоступные пониманию обычного человека — не верьте. Есть много сугубо практических задач, о существовании которых настоящие математики не подозревают, или их решение им не интересно из-за отсутствия достаточного хайпа вокруг них, или потому что у них есть примерное представление путей достижения для их решения. Не бойтесь браться за задачи, решение которых отсутствует в википедии, не бойтесь публиковать их решения и не бойтесь читать комментарии под статьями о бесполезности всего сущего.