Как найти иголку в стоге сена? Или обозор Retrieval Algorithms02.09.2024 12:16

Появление трансформеров, а впоследствии LLM (Large Language Models) привело к активному распространению чат-ботов и различных ассистентов помогающих в получении информации или генерации контента. Но несмотря на то что LLM способны по запросу генерировать человекоподобные тексты, они подвержены галлюцинациям. Естественным кажется желание уменьшить количество недостоверных ответов. Для этого мы можем либо дообучить LLM на наших данных, либо использовать Retrieval Augmented Generation (RAG).

RAG — это способ генерации текстов на новых данных без дообучения модели, с помощью добавления релевантных документов в промпт. Документы для генерации ищутся с помощью retrieval системы, после чего объединяются в один промпт и подаются в LLM для последующей обработки. В этой статье я решил собрать информацию о всех наиболее известных и применяемых алгоритмах поиска, с описаниями и материалами для более глубокого изучения.

Задача retrieval системы состоит в том, чтобы по некоторому запросу находить в базе знаний top-k подходящих документов. Для определения «подходящего» документа используются функции схожести (similarity function). Основываясь на них, подходы к поиску можно выделить в 3 категории:

Sparse Retrieval
Dense Retrieval
Другие

Разреженный поиск (Sparse Retrieval)

Скрытый текст

Sparse Vector — высоко размерный вектор, содержащий относительно небольшое количество ненулевых значений, поэтому он — sparse (разреженный).

Sparse методы, за счет своей простоты и высокой скорости работы, часто используются в поисковых системах. Они могут выступать как основным алгоритмом поиска, так и в качестве алгоритма выбора кандидатов для последующего реранжирования. Разреженные методы основаны на анализе частотности вхождений слов в документы.

Преимущества

Быстрый поиск
Хороший baseline
Не требуется обучение моделей
Интерпретируем

Недостатки

Работа только с текстовыми данными
Не сможет найти похожие по смыслу документы, в которых нет ключевых слов из запроса

TF-IDF

Рассмотрим метод поиска с использованием Term Frequency — Inverted Document Frequency (TF-IDF). TF-IDF подсчитывает значимость каждого слова в документе и корпусе документов.

Term Frequency (частота термина) считается как отношение числа вхождений слова в документ деленное на количество слов в документе

$TF(t, d) = { n_t \over |d| }$

где — слово (термин), — документ, |d| — число слов в документе, n_t — число вхождений слова в документ.

Invert Document Frequency (обратная частота документа) — инверсия частоты, с которой некоторое слово встречается в корпусе документов

$IDF(t, D) = log { |D| \over |\{d_i \in D | t \in d_i\}|}$

где — слово (термин), |D| — число документов в корпусе, | ${d_i \in D | t \in d_i}|$ — число документов из корпуса , содержащих слово .

IDF — это константа, которая уменьшает вес широко употребляемых слов. Поэтому основание логарифма в формуле можно выбрать любым. Ведь это не сможет изменить соотношение весов.

Term Frequency — Inverted Document Frequency получим перемножением функций TF и IDF

$TF{-}IDF(t, d, D) = TF(t, d) \cdot IDF(t, D)$

Таким образом, вес слова в документе будет большим, если у слова высокая частота употребления в рамках документа и низкая в остальных документах корпуса.

Алгоритм поиска:

Получение векторов каждого документа в корпусе с помощью TF-IDF
Формирование вектора из текста запроса
Подсчет дистанций от вектора запроса до векторов документов
Сортировка в порядке уменьшения релевантности

Полезные ссылки

BM25

Скрытый текст

BM — Best Match или лучшее совпадение. 25 означает, что формула получена с 25 попытки.

BM25 (Best Match 25) — функция ранжирования, используемая для оценки релевантности документов в системах поиска информации. По своей сути является улучшением TF-IDF. Поскольку использует анализ частотности появления общих слов в документе и запросе для выдачи оценки релевантности.

В общем случае, формулу подсчета релевантности документа из корпуса запросу $Q = \{q_1, ...., q_n\}$ можно выразить следующим образом:

$BM25(Q, d) = \sum_{i=1}^n {TF(q_i, d) \cdot (k_1 + 1) \over TF(q_i, d) + k_1 \cdot (1 - b + b {|d| \over avdl })} \cdot IDF(n_i, |D|)$ $IDF(n_i, |D|) = log( {(|D| - n_i + 0.5) \over (n_i + 0.5)}+1)$

где

Первый множитель — это нормированный TF из формулы TF-IDF. В формуле присутствуют гиперпараметры k_1 и, которые задаются для конкретной системы, согласно улучшаемой метрике. Эксперименты показывают, что k_1 иследует выбирать в следующих диапазонах 0.5 < b < 0.8, 1.2 < k_1 < 2. В знаменателе делаем нормировку с учётом длины документа — это норма, т. е. количество слов в документе, делённое на среднюю длину документа в корпусе документов — avdl .

Значение первого множителя тем больше, чем чаще слово встречается в документе. Например, если вы ищете что-то про котов, и в каком-то коротком тексте слово «кот» встречается 50 раз, то это означает, что документ с высокой вероятностью релевантен вашему запросу.

Второй множитель — это сглаженный вариант IDF, полученный из веса релевантности Robertson-Sparks-Jones (формула 3, стр. 6). Чем реже встречается слово, тем выше ценность каждого попадания этого слова в документ. Другими словами, «штрафуем» очень частые слова, снижая их вес.

Если посмотрим внимательно на дробь под логарифмом, то заметим, что при , где — размер выборки. Считается что логарифмическая сложность достигается в том случае, если $N \ge 2^D$ , поэтому данный алгоритм не дает преимущества перед полным перебором даже при D = 100

Полезные ссылки

Random Projection Trees

Алгоритмы использующие деревья для нахождения ближайших соседей довольно частое явление. Идея такого рода алгоритмов заключается в итеративном разделении пространства случайными гиперплоскостями и построения на базе разделения дерева, в листах которого содержится малое число объектов.

Одним из таких алгоритмов является ANNOY. ANNOY — алгоритм от Spotify, предназначенный для рекомендаций музыки. Данный алгоритм похож на KD-Tree, за исключением способа разбиения пространства. Для каждого разбиения выбираются две случайные точки, их соединяют в отрезок, а затем через середину отрезка строится перпендикулярная гиперплоскость.

Разбиение продолжается до тех пор пока в одной из нод дерева не окажется объектов меньше чем K (K — гиперпараметр). Таким образом получаем бинарное дерево с глубиной порядка O(logN) в среднем.

Для поиска ближайших соседей для некоторой точки достаточно спуститься по дереву в лист и взять из него требуемое количество соседей. Но вероятна ситуация, когда содержащихся в листе соседей не хватает. В таком случае предусмотрены хаки:

Очередь с приоритетом
В нее добавляются посещенные ноды, и с некоторым трешхолдом можем выбирать насколько далеко сможем уйти в «ошибочную» сторону
Построение леса деревьев
Вместо того чтобы строить 1 дерево строим несколько. За счет случайности выбора точек получим различные деревья. Таким образом спустившись до листа в каждом из деревьев и объединив точки в них получим хороших соседей

Подробнее про ANNOY можно почитать тут.

Достоинства подхода

Проблемы подхода

Использует много памяти
Плохо параллелиться и переносится на GPU
Добавление новых данных требует перезапуска всего процесса создания дерева

Полезные ссылки

Locality Sensitive hashing (LSH)

Хэш функции сопоставляют объектам числа, или бины. Locality sensitive hash (LSH) функция сопоставляющая похожие объекты в один хэш бин, а непохожие объекты в другие бины. Подругому, LSH пытается объединить похожие объекты в один хэш бин.

Если два объекта имеют один хэш, то это коллизия. В случае LSH функций появление коллизии имеет вероятностный характер. Поэтому определение LSH функции основано на ее вероятности коллизии.

Определим формально семейство хеш-функций, которое мы хотим использовать.

Назовем семейство хэш-функций к функции расстояния , если для любой хэш-функции $h(x) \in H$ , получаем:
Если $d(x , y) \le R$ , тогда вероятность коллизии $Pr[h(x) = h(y)] \ge p_1$
Если $d(x , y) \ge cR$ , тогда вероятность коллизии $Pr[h(x) = h(y)] \le p_2$

Img. 1. Источник

На изображении 1 можно увидеть смысл определения. В нем говорится, что, если взять LSH функцию из семейства , вероятность коллизии для точек находящиеся в круге радиуса (красная зона) от точки запроса будет не меньше p_1 . А для точек вне окружности радиуса (синей зоне) не больше p_2 . Точки в серой зоне нам не интересны.

Одним из простых примеров LSH функции является Signed Random Projections. Она строится на основе разбиения пространства гиперплоскостями. Для каждой плоскости определяется по какую сторону лежит точка, и кодируется информация в 1 бит, т.е проставляется флаг: 1 или 0. Таким образом дляплоскостей получается вектор изнулей и единиц. Для их сравнения может быть использовано расстояние Хэмминга.

Данный подход стал классическим, что означает на его смену пришли более продвинутые методы, но он все равно хорош. Один из сменивших его алгоритмов является Product Quantization.

Полезные ссылки

Product Quantization (PQ)

PQ популярный метод сильного сжатия многомерных векторов, позволяющий использовать на 97% меньше памяти, а также повышает скорость поиска ближайших соседей. Таким образом данный подход чаще всего используется, когда данных настолько много, что хранить их даже на диске дорого.

Рассмотрим работу данного алгоритма на примере. Пусть размер векторов 1024, это могут быть эмбеддинги для текстов или изображений. Если каждое значение вектора представлено числом с плавающей точкой FP32, то каждый вектор будет весить 4 килобайта, а 30 миллионов таких векторов около 120 ГБ.

Что бы оптимизировать поиск по такому датасету, проделаем следующее:

Разбиваем каждый вектор на подвектора размером 128, получаем 8 наборов векторов
Кластеризируем каждый из 8 наборов с помощью k-means, с числом кластеров равным 256 (в 1 байт может быть записано число от 0 до 255)
Записываем новые вектора состоящие из ID кластеров каждого из подвекторов и сохраняем центроиды кластеров

Для поиска ближайших соседей будем считать расстояния между запросом и базой знаний. Существует два вида подсчета расстояний симметричный и асимметричный.

Symmetric distance computation (SDC)
При данном подходе векторы запроса и базы знаний представляются в виде центроидов своих кластеров.

Asymmetric distance computation (ADC)
Расстояние считается между неизменненным вектором запроса и центроидами векторов базы знаний.

На основе данного подхода строится Inverted File Index, что позволяет улучшить поиск. О том как это работает в FAISS можно прочитать тут.

Полезные ссылки

Hierarchical Navigable Small World (HNSW)

На данный момент State-of-the-Art (SotA) алгоритмы векторного поиска основаны на графах близости. Наиболее популярным алгоритмом является Navigable Small World (NSW).

Navigable Small World

Img. 2. NSW граф, черным выделены короткие ребра, красным - длинные. (Источник)

Img. 2. NSW граф, черным выделены короткие ребра, красным — длинные. (Источник)

Применение алгоритма возможно только после построения графа (он также называется NSW). Выделим основные его свойства:

Нода графа является документом (эмбеддингом, вектором)
Ребро — запись в таблице, указывающая на возможность перехода из одной ноды в другую
Переходы взаимно обратны, формально граф неориентированный
Ребра должны представлять как длинные, так и короткие связи
Средняя степень вершин мала, т.е количество ребер выходящих из вершины мало

Построение графа

На этом этапе можно посчитать расстояния до большого числа точек, так как предварительная работа выполняется разово.

Для каждой ноды случайно выбираем $5-10 \%$ нод до которых будут считаться расстояния. После подсчета расстояний выберемближайших и из них случайным образом выбираем $n, n \le m$ нод до которых будут проложены ребра. Аналогично, берем максимально удаленные ноды и прокладываем до них ребра. Получим граф похожий на Img. 2.

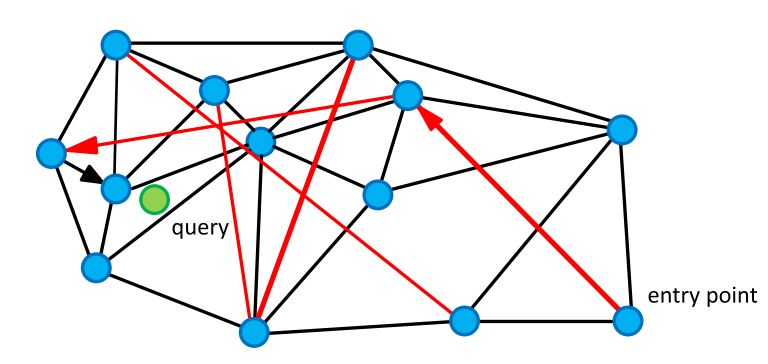
Поиск

На вход поступает запрос (зеленый на Img.2.). Для нахождения его ближайших соседей достаточно выбрать случайную ноду посчитать расстояния от связанных с ней вершин до запроса. Найти вершину с наименьшим расстоянием и переместиться в нее. Итеративно повторив описанную процедуру, найдем точку наиболее близкую к запросу.

Для улучшения качества поиска и нахождения наиболее близких точек к запросу, применяются множественная инициализация и очередь с приоритетом.

Используя NSW нередкая проблема возникает с тем, что можно застрять в плотном кластере нод из которого нет возможности выбраться.

Hierarchical Navigable Small World

Img. 3. HNSW (Источник)

В названии метода отражена его суть. Авторы подхода заметили, что перебор длинных связей в начале с постепенным спуском к более локальным связям (Img. 3.) выгоднее обычного NSW подхода.

Более формально, поиск разбит на уровни. Слой L = 0 содержит все точки (аналогично NSW), L = 1 cодержит некоторое подмножество исходных точек, таким образом последний слой будет содержать малое число точек.

Построение графа

Основная идея для построения иерархичного NSW заключается в том что бы распределить по слоям ноды в зависимости от их расстояния друг от друга. Таким образом на верхние слои попадают ноды максимально удаленные друг от друга, и с продвижением вглубь расстояния между нодами будет уменьшаться.

Поиск

Поиск начинается на верхнем уровне. Аналогично NSW алгоритму находим ближайшую точку к запросу. После это спускаемся на слой ниже и повторяем операцию, можно начинать поиск на новом слое не из одной точки, а из нескольких ближайших с предыдущего слоя. Повторяя процедуру, спускаемся на нулевой слой. После чего выбираем ближайших соседей.

HNSW является передовым методом поиска ближайших соседей, который на практике часто показывает лучшие результаты по сравнению с другими приближёнными методами. Он позволяет гибко настраивать баланс между точностью и скоростью работы, а также имеет простую и понятную структуру. К тому же, существует эффективные реализация этого алгоритма в библиотеках nmslib и FAISS.

Однако HNSW имеет и свои недостатки. Алгоритм требует значительных затрат памяти, так как для каждого слоя необходимо хранить вершины и рёбра графа. Также он не поддерживает сжатие векторных представлений, что может ограничивать его применение в некоторых задачах. Несмотря на эти ограничения, HNSW остаётся одним из наиболее эффективных и надёжных методов для решения задач поиска ближайших соседей.

Полезные ссылки

Для сравнения ANN алгоритмов создан фреймворк позволяющий проводить бенчмарки различных алгоритмов на разных датасетах. Найти его можно здесь.

Другие

Кроме разреженного и плотного поиска, существуют альтернативные методы для извлечения релевантных объектов.

Для поиска релевантного кода, исследователи используют редакционные расстояния между текстами и абстрактные синтаксические деревья (AST).

Для работы с неструктурированными текстами, строятся графы знаний. В таких графах сущности связаны отношениями, которые служат заранее построенным индексом для поиска. Таким образом, методы использующие графы знаний, могут применять k-шаговые поиски соседей для извлечения информации.

Еще одним методом поиска является распознавание именованных сущностей (Named Entity Recognition, NER), где запрос является входными данными, а сущности выступают в роли ключей. В этом методе идентификация и выделение именованных сущностей в тексте позволяют использовать их в качестве точек поиска для нахождения релевантной информации.

Полезные ссылки

Выводы

Выбор метода поиска сильно зависит от данных среди которых производится поиск.

Sparse методы довольно просты и быстры, но могут быть применены только для текстовых данных. Dense методы позволяют искать информацию по любым модальностям и точнее разреженных, при этом занимают больше памяти, а добавление новых элементов для поиска дороже. Альтернативные методы относительно новое явление, но показывают хорошие результаты в поиске текстовых данных. Например, для построения графа знаний требуется много времени и ресурсов, но генерация, на основе найденных текстов, становится более точная и человекоподобная.

Полезные ссылки

Retrieval-Augmented Generation for AI-Generated Content: A Survey
Sparse Vector Search
SPLADE for Sparse Vector Search Explained
Учебник по машинному обучению: Метрические методы