Как глубока Бездна Челленджера: измерение глубины15.04.2020 09:48

«Надо понимать всю глубину наших глубин» © ДМБ

Приветствую вас, глубокоуважаемые!

Всегда поражался, что расстояние до луны измеряется с миллиметровой точностью. Даже при открытии экзопланет методом лучевых скоростей, скорости звезд измеряются с точностью до 0.97 м/с.
А вот, например, глубина Бездны Челленджера определена с точностью ± 10 метров.
Почему же с водой все так сложно?

С этим вопросом разбираемся под катом. В качестве вишенки на торт: приложение для визуализации движения звука через воду со слоями разной плотности с исходниками на гитхабе и онлайн-калькулятор.

Напомню, что есть ровно два с половиной фундаментальных способа определения глубины:

веревкой =)
манометрический, когда глубину определяют по давлению столба жидкости. Принципиальные проблемы, связанные с этим методом я описал в первой части манускрипта. Вкратце: нужно учитывать атмосферное давление, географическую широту (с ней меняется ускорение свободного падения) и изменение плотности воды от температуры, давления и солености.
по времени распространения звука — эхолотом.

Вот с последним пунктом сегодня и предлагаю разобраться.

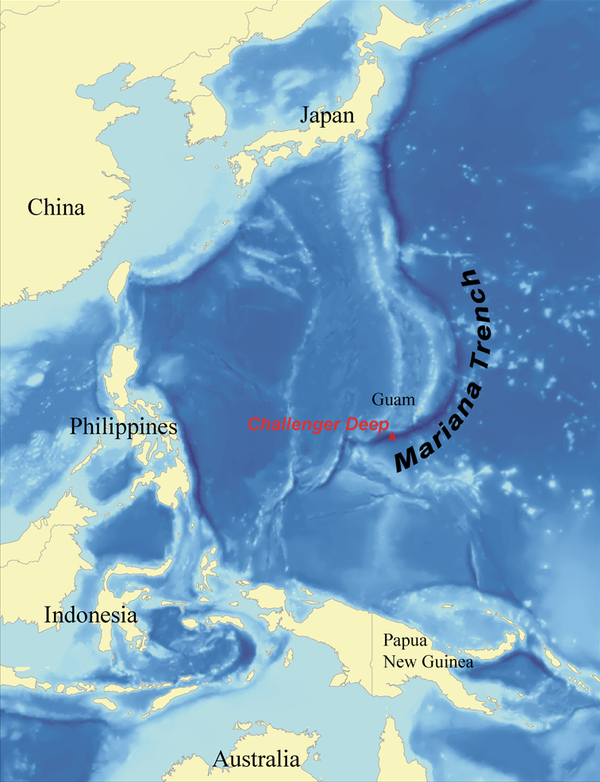
Я люблю всегда рассматривать ситуацию в пределе. Марианская впадина в целом и Бездна Челленджера в частности — это и есть предел ситуации с глубиной на нашей планете. Многие эффекты становятся существенны и отчетливо видны только на больших глубинах.

Итак, история измерения больших глубин берет свое начало от того самого Челленджера — HMS Challenger, чье имя и носит самая глубокая впадина земного океана. Вот, кстати он на фото:

Весной 1875 года экспедиция измерила при помощи веревки глубину, ни много ни мало — 8184 метров. К слову, проблемы измерения глубины веревкой помимо таких очевидных как дрейф судна и течения, описаны в Занимательной Физике у Перельмана: веревка испытывает трение об воду, извивается, скручивается как молекулы белков и вниз, после определенной глубины, уже не идет — не принимает вода ее.

С тех пор люди не сидели без дела и в 1952 году глубины марианской впадины измерял уже HMS Challenger II:

При помощи взрывчатки, ручного секундомера, проволоки с грузом в 20 кг, лома и скотча, а также первых эхолокаторов они намерили уже 10900 метров. После постобработки результат уменьшили до 10632 м с неоднозначностью в ± 27 метров.

Раскапывая, или что атмосфернее, погружаясь в историю исследования мирового океана, в одной из прошлых статей я упомянул легендарное советское исследовательское судно «Витязь» — в качестве КДПВ использовал изображение почтовой марки с ним:

В 1957 году «Витязь» измерил самую глубокую глубину наших глубин — 11034 м. Измерения были сделаны на пределе диапазона эхолота исходя из постоянной скорости звука в 1500 м/с, после чего были взяты бутылочные пробы воды для построения профиля температуры и солености, по которым в последствие и было получено значение в 11034 метра. Хоть этот результат и попадается всюду, где речь заходит о марианской впадине, современные специалисты смотрят на него скептически.

Далее в 1960 акванафты с Триеста сообщили об измерениях по бортовому датчику давления 10911 метров, а судно сопровождения, при помощи взрывчатки измерило глубину в 10915 ±20 метров. А уже в 1976 при помощи эхолота получили значение 10933 ± 50 метров.

Откуда берутся все эти ±20 и 50? Вдумчивый читатель скорее всего давно сообразил к чему я клоню — скорость звука в воде зависит от температуры, солености и давления, т.е. от плотности среды.

Профиль температуры и солености — это набор измерений с привязкой к глубине.
И ни температуру, ни соленость нельзя измерить дистанционно — необходимо «сунуть» термометр и кондуктометр в нужную точку океана. Желательно сделать много измерений по линии как можно вертикальнее и через каждый метр.

Вот так выглядят некоторые профили:

«Академик Иоффе», 30 марта 2005.
Место измерения на гуглокартах

Американское исследовательское судно «OCEANUS», 10 апреля 2010.
Место измерения на гуглокартах
Кстати, на этом океанусе даже вебкамера есть.

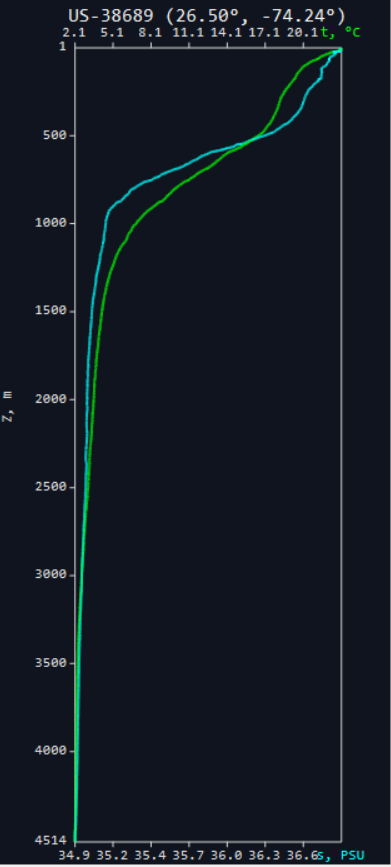
Судно NOAA «RONALD H. BROWN», 20 октября 2001.
Место измерения на гуглокартах

История измерения самой глубокой точки не бедна и курьёзами

В 1992 году (казалось бы!) экспедиция университета Токио измерили глубины как наши соотечественники в 1957 — исходя из постоянной скорости звука в 1500 м/с, но по какой-то причине не собрали профили температуры и солености. Вместо этого они откорректировали данные по таблицам 1980 (!) года и получили значение в 10933 м без указания погрешностей.

Уже в 2002 экспедиция на судне Keirei Японского агентства науки и технологий по изучению морских недр (JAMSTEC) проводила исследования по поиску глубочайшей глубины при помощи довольно продвинутого многолучевого эхолота. Они получили значение в 10920 ±5 м. Они собрали большое количество профилей, но отказ термометра-кондуктометра вынудил их воспользоваться профилями двухлетней давности.
Японцам периодически невезло.

Позднейшие измерения

В 2008 исследователи из университета Гавайев вот на таком красавце Kilo-Moana

Получили глубину в 10903 метра при помощи многолучевого эхолота EM 120 от Kongsberg Maritime.

В 2010 ученые из университета Нью Хемпшира на USNS Sumner при помощи более новой модели EM 122 от тех же норвежцев получили глубину 10944 ± 40 м в точке (позиция на гуглокартах).

В конечном счете

Неоднозначности при определении глубин при помощи эхолотов есть следствия следующих факторов:

Погрешности измерения, которая в свою очередь включает и погрешность самого прибора, его угловое разрешение (луч 1°х1° дает пятно диаметром в 140 метров на дне впадины), размытие пика, рефракцию, качку судна, его перемещение и т.д и т.п.)
Наличие и изменчивость профиля скорости звука — его нельзя измерить, положить данные на полку, а через два года воспользоваться — такие данные интересны только в ретроспективе, мол, а вот взгляните, тогда было вот так, а сейчас — совсем иначе.
Несовершенство методов постобработки

Здесь я могу хочу коснуться только одного из факторов — профиля температуры и солености, или, что в нашем случае почти одинаково — профиля скорости звука.
Просто чтобы наглядно оценить: каков эффект?

Мы принимаем допущение о том, что звук у нас почти как мячик от пинг-понга — путешествует исключительно вертикально, отскакивает от дна весь целиком, корабль неподвижен, дно ровное. Время мы измеряет без погрешностей. И единственное что нас путает — наличие профиля скорости звука.
Как при этом он повлияет на измеряемую глубину?

В этом случае наша модель может быть описана простой формулой:

$s=\sum{v(t_i)\Delta t}$

Где $s$ — пройденный звуком путь, $v(t_i)$ — скорость звука в i-й интервал времени, длительность которого $\Delta t$ .

Если мы уменьшаем $\Delta t$ (а мы не можем) то дело идет к интегралу из школьной физики:

$s=\lim_{\Delta t\rightarrow 0}{\sum{v(t_i)\Delta t}}$

$s=\int{v(t)dt}$

Далее, исходя из измеренного времени распространения звука (от начала излучения до приема отраженного сигнала) нам нужно:

через равные временные промежутки примерно прикидывать глубину (с точностью, но десятка-другого метров)
интерполировать (если необходимо) из имеющегося профиля температуру и соленость для прикинутой глубины
по ней вычислять скорость звука, а соответственно и путь, который звук прошел на этой глубине за временной интервал.

Для этих (и других) целей я запилил библиотеку, про которую говорил в первой части статьи. На данный момент она реализована на C/C#/Rust/Matlab/Octave/JavaScript.

Скорость звука считается по формуле Чена и Миллеро. Она нравится мне потому, что там параметром идет давление, которое измеряется непосредственно, а не глубина, как в других моделях. Плюс диапазон по параметрам у этой модели покрывает почти все разумные случаи.

Например, для второго профиля, который получен в этой точке 10 апреля 2010 года, разница между глубиной, полученной по стандартному значению скорости звука и глубиной, полученной по приведеному выше расчету при времени распространения 5 секунд (туда и обратно) получается 18 метров: 3750 против 3768.3 метров, а для 6 секунд разница возрастает до 32 метров.
К сожалению у меня нет профиля из марианской впадины, и вообще мне пока не попадался ни один профиль глубже 6000 метров. Но если принять, что после 4–5 км глубины параметры меняются слабо и скорость звука в основном меняется из-за давления, то получается, что для обсуждаемых глубин разница получается порядка 420 метров, а время от момента излучения сигнала эхолотом до принятия отражения составляет более 14 секунд.

В качестве демонстрационных материалов имеется:

онлайн-калькулятор, в котором можно вручную ввести профиль или использовать одни из трех, так сказать, hard-coded.

Поскольку я толком ничего не смыслю в JavaScript, то мне проще было сделать спустя рукава визуализацию на C#. Проект я положил на GitHub.
Я знаю, что все знают, но опыт показывает что лучше дать прямую ссылку и на Release

Окно приложения выглядит вот так: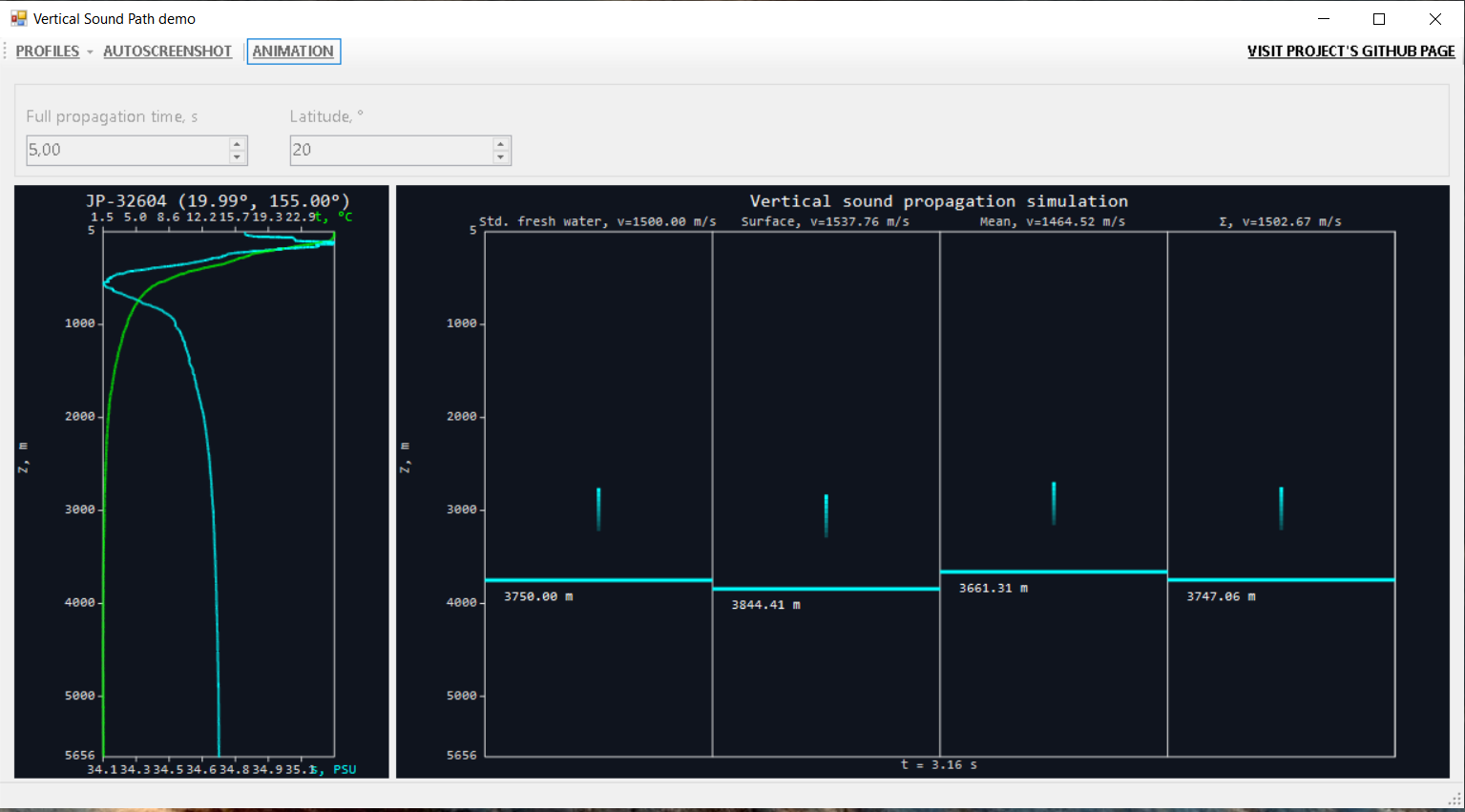

По умолчанию стоит время распространения 5 секунд и какой-то профиль с северной части тихого океана всего из 13 точек.

Справа 4 колонки, в каждой из которых (после нажатия кнопки ANIMATION конечно) звук начинает путешествовать с разной скоростью:

в первой — 1500 м/с (стандартное значение для пресной воды),
во второй — со скоростью, вычисленной по температуре и солености с поверхности воды,
в третьей — со скоростью, вычисленной по средней температуре и солености для профиля
в четвертой — с пересчетом скорости для каждого шага и суммирование пройденного пути

Отображение заведено на MMTimer с периодом в 0.01 с, с этим же периодом работает и симуляция.

В меню PROFILE можно выбрать один из трех демо-профилей (в них мало точек), также можно загрузить несколько профилей, выдранных мной из World Ocean Database которую бережливо собирает NOAA.
Эти профили лежат в виде CSV и помимо всего прочего содержат информацию о месте замера, времени, стране, управляющем институте и судне, на котором он производился. Более подробно об этом я писал в статье «Кто и как исследовал мировой океан: разбираем базы NOAA».

Совсем для ленивых (каюсь, я такой же) я собрал GIF-анимацию, но GIF везде отображается по-разному, и «полного эффекта присутствия» не получится:

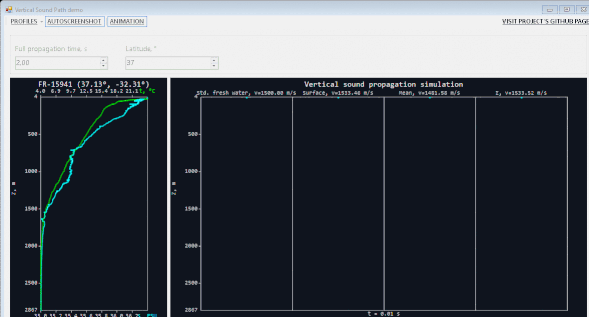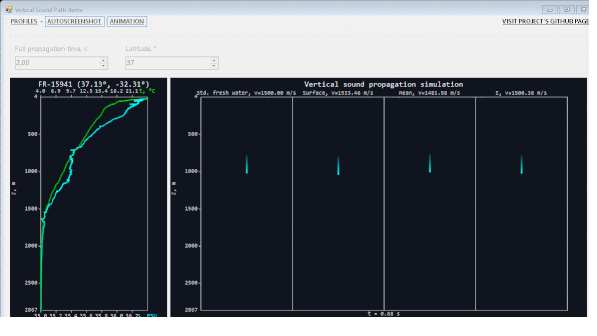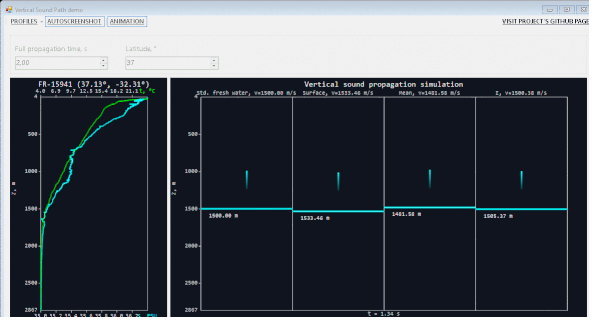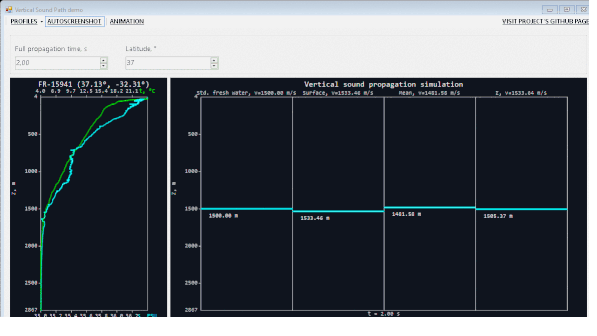
При написании исторического обзора про исследование марианской впадины я пользовался статьей Джеймса Гарднера с сотоварищами. Крайне рекомендую для интересующихся. Там очень хорошо описаны сложности при измерении, казалось бы, такой «простой» вещи, как глубина.

P.S.

Хочу поблагодарить всех тех, кто голосовал в предыдущей статье. За то, чтобы появилась эта, было отдано аж 109 голосов — ребята, это для вас! Те двое, кто был против — пардон, я прислушался к мнению большинства.

P.P. S.

Традиционно буду искренне (для меня это не пустое слово) благодарен за сообщения об ошибках, конструктивную критику, интересные вопросы и дискуссии.