Как аппроксимировать любую функцию с помощью PyTorch19.04.2024 02:30

При анализе данных и построении моделей машинного обучения часто возникает необходимость аппроксимировать сложные функции. PyTorch предоставляет удобные инструменты для создания и обучения нейронных сетей, которые могут быть эффективно использованы для этой цели. В этом посте мы рассмотрим простой пример аппроксимации функции с использованием PyTorch.

Шаг 1: Подготовка данных

Давайте начнем с простого примера из теории управления и решим его сначала аналитически, а затем с использованием PyTorch. Рассмотрим функцию

$\ddot{x}+\dot{x}+x=u$

Это линейное неоднородное дифференциальное уравнение, где x(t) представляет собой выход системы, — входной сигнал, а $\dot{x}$ и $\ddot{x}$ обозначают, соответственно, первую и вторую производные x(t) по времени .

Тогда характеристический полином будет выглядеть

$\lambda^2+\lambda+1=0\\\lambda=-\frac{1}{2}\pm\sqrt{3}i$

После нахождения корней характеристического уравнения мы можем записать общее решение дифференциального уравнения в виде комбинации экспоненциальных функций. Поскольку корни комплексные, мы можем использовать формулу Эйлера, чтобы выразить решение в терминах косинусов и синусов

$x(t)=C_1\cdot e^{-\frac{1}{2}t}\cos(\sqrt{3}t) + C_2 \cdot e^{-\frac{1}{2}t}\sin(\sqrt{3}t)$

где C_1 и C_2 — произвольные постоянные, которые определяются начальными условиями задачи. Давайте в нашей задаче x(0)=1 и $\dot{x}(0)=2$ . Тогда можно полностью определить решение нашей задачи

$x(t)=\frac{4}{\sqrt{3}} \cdot e^{-\frac{t}{2}} sin(\frac{\sqrt{3}t}{2}) - 2 e^{-\frac{t}{2}} cos(\frac{\sqrt{3}t}{2})$

Давайте промоделируем отклик системы для начальных условий $[x, \dot x]=[1, 2]$ помощью библиотеки control

init_state = [1, 2]
dt = 0.001
time = np.linspace(0, 10, int(time/dt))

# create transfer function
numerator = [1]
denominator = [1, 1, 1]
system = ctrl.tf(numerator, denominator)

# get respomse from the TF
response = ctrl.initial_response(system, time, init_state).outputs
plt.plot(time, response, label="Impulse response of the system")

Именно time, response мы позже будем использовать как обучающий датасет. Также заодно изобразим аналитическое решение задачи.

class Analytic:
    def __init__(self, alpha, beta, c_1, c_2):
        self.alpha = alpha
        self.beta = beta

        self.c_1 = c_1
        self.c_2 = c_2 
    
    def calculate(self, t: float) -> float:
        return self.c_1 * np.exp(self.alpha * t) * np.sin(self.beta * t) \
             + self.c_2 * np.exp(self.alpha * t) * np.cos(self.beta * t)
    
    def __call__(self, t: list[float]) -> list[float]:
        return np.vectorize(self.calculate)(t)

analytic = Analytic(
    alpha = -0.5,
    beta = np.sqrt(3)/2,
    c_1 = 4/np.sqrt(3),
    c_2 = 2
)

plt.plot(time, analytic(time), linestyle="--", 
         label="Analityc solution")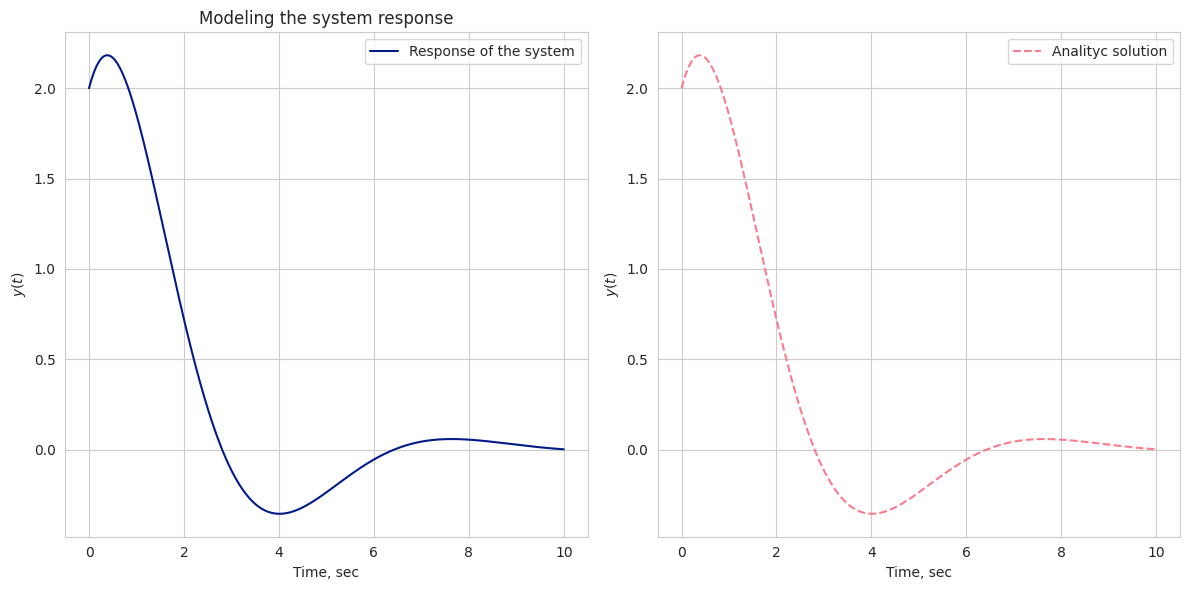

Смоделированное решение и аналитическое.

Шаг 2: Определение модели

Теперь надо определиться с архитектурой модели. Для нас это будет обычной функцией вида

$y(t)=C_1\cdot e^{\alpha\cdot t} \cdot \sin(\beta t)+ C_2 \cdot e^{\alpha\cdot t} \cdot \cos(\beta t)$

где

α: обучаемый параметр nn.Parameter, представляющий собой коэффициент экспоненциального роста.
β: Фиксированное значение (установлено на $\frac{\sqrt{3}}{2}$ ): представляющее собой частоту осцилляции. Позже расскажу почему фиксированное.
и : Обучаемые параметры, представляющие коэффициенты для синусоидальных и косинусоидальных членов соответственно.

Теперь давайте напишем нашу модель с использованием PyTorch. Ниже приведен пример кода для создания модели:

class Model(nn.Module):
    """Our class that will be trained"""

    def __init__(self):
        super().__init__()
        self.alpha = nn.Parameter(torch.zeros(1))
        self.beta = np.sqrt(3)/2
            

        self.c_1 = nn.Parameter(torch.zeros(1))
        self.c_2 = nn.Parameter(torch.zeros(1))
        
    def forward(self, t):
        return self.c_1 * torch.exp(self.alpha * t) * torch.sin(self.beta * t) \
             + self.c_2 * torch.exp(self.alpha * t) * torch.cos(self.beta * t)y

Этот код определяет класс Model, который наследуется от класса nn.Module в PyTorch. В методе init мы определяем обучаемые параметры alpha, C1 и C2, а также фиксированную частоту beta. В методе forward определяется прямой проход модели, где мы вычисляем выходное значение output в зависимости от входной переменной t с использованием заданных параметров.

Для обучения модели нам нужно написать класс датасет, наследник класса torch.utils.data.Dataset.

class TimeResponseDataset(Dataset):
    """Torch Dataset for x=time and y=response"""
    def __init__(self, time, response):
        self.time = torch.Tensor(time)
        self.response = torch.Tensor(response)
        
    def __len__(self):
        return len(self.time)
    
    def __getitem__(self, idx):
        return {'time': self.time[idx], 'response': self.response[idx]}

Он нам нужен, чтобы позже закинуть его в torch.utils.data.DataLoader. Он то и будет нам выдавать батчи данных во время обучения.

dataset = TimeResponseDataset(time, response)
dataloader = DataLoader(dataset, batch_size=512, shuffle=True)

Шаг 3: Обучение

Давайте посмотрим количество обучаемых параметров в модели.

model = Model()
print(f"trainable params: {len([i for i in model.parameters()])}")

Результат, как мы и задумывали, равен 3.

Проинициализируем лосс функцию и оптимизатор. Лосс функция будет говорить нам как далеко нам до оптимума, а оптимизатор будет определять как быстро и в каком направлении менять веса, чтобы добраться до него.

lr = 0.01
betas = (0.9, 0.999)
history = []

criterion = nn.MSELoss() 
optimizer = torch.optim.Adam(model.parameters(), lr=lr, betas=betas, eps=1e-8)

Теперь обучим модель на 150 эпохах, сохраняя при этом историю лосс функции.

epochs = 150
for epoch in tqdm(range(epochs)):
    for i, data in enumerate(dataloader):
        optimizer.zero_grad()
        pred = model(data['time'])
        loss = criterion(pred, data['response'])
        loss.backward()
        optimizer.step()
        
        history.append(loss.detach().numpy())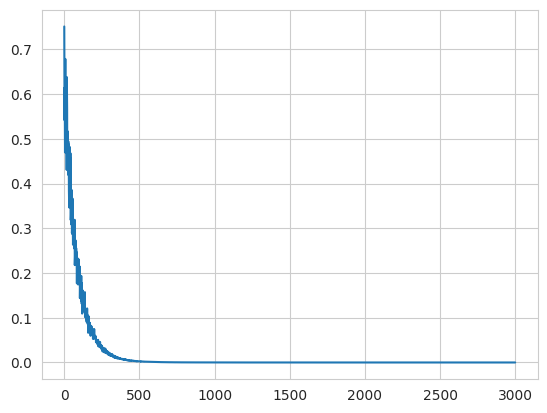

MSE в течение обучения.

Приведен график лосс функции от количества батчей обучения. Как видно из графика модель сошлась еще на 500 шаге. Давайте посмотрим на обученные параметры и на аналитическое решение.

Шаг 4: Сравнение

analytic.alpha, analytic.c_1, analytic.c_2

[-0.5, 2.3094, 2]

estimation = [float(param.data) for param in model.parameters()]
estimation

[-0.49999, 2.30939, 2.00000]

Ошибка меньше $0.01\%$ . Давайте посмотрим на то, как хорошо легла наша модель под реальные данные.

approx = Analytic(
    alpha=estimation[0],
    beta=model.beta, 
    c_1=estimation[1],
    c_2=estimation[2]
)

# Analytic, we defined earlier
plt.plot(time, analytic(time), color[0], 
        label="$y=4/\sqrt{3} \cdot e^{-t/2} sin(\sqrt{3}t/2) - 2 e^{-t/2} cos(\sqrt{3}t/2)$.")

# Approximation
plt.plot(time, approx(time), color[2], linestyle='--', label='Approximation')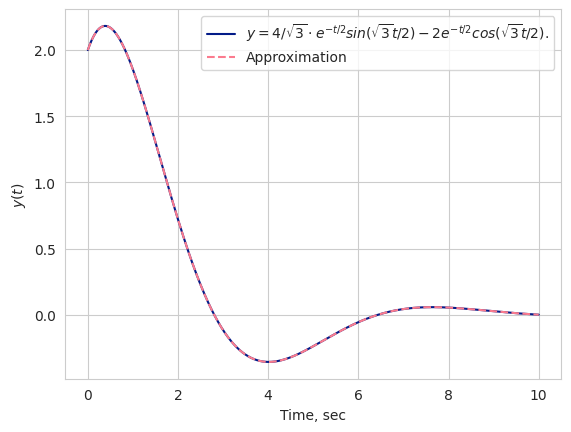

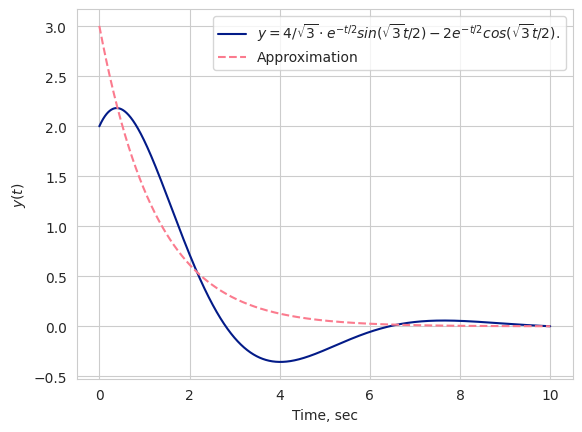
Аппроксимация исходной функции torch моделью.

Чтобы осознать как быстро сходится модель на этой задаче, можно посмотреть на графики ниже. Это сравнение аналитического решения и нашей модели на эпохах 0, 10, 20 .

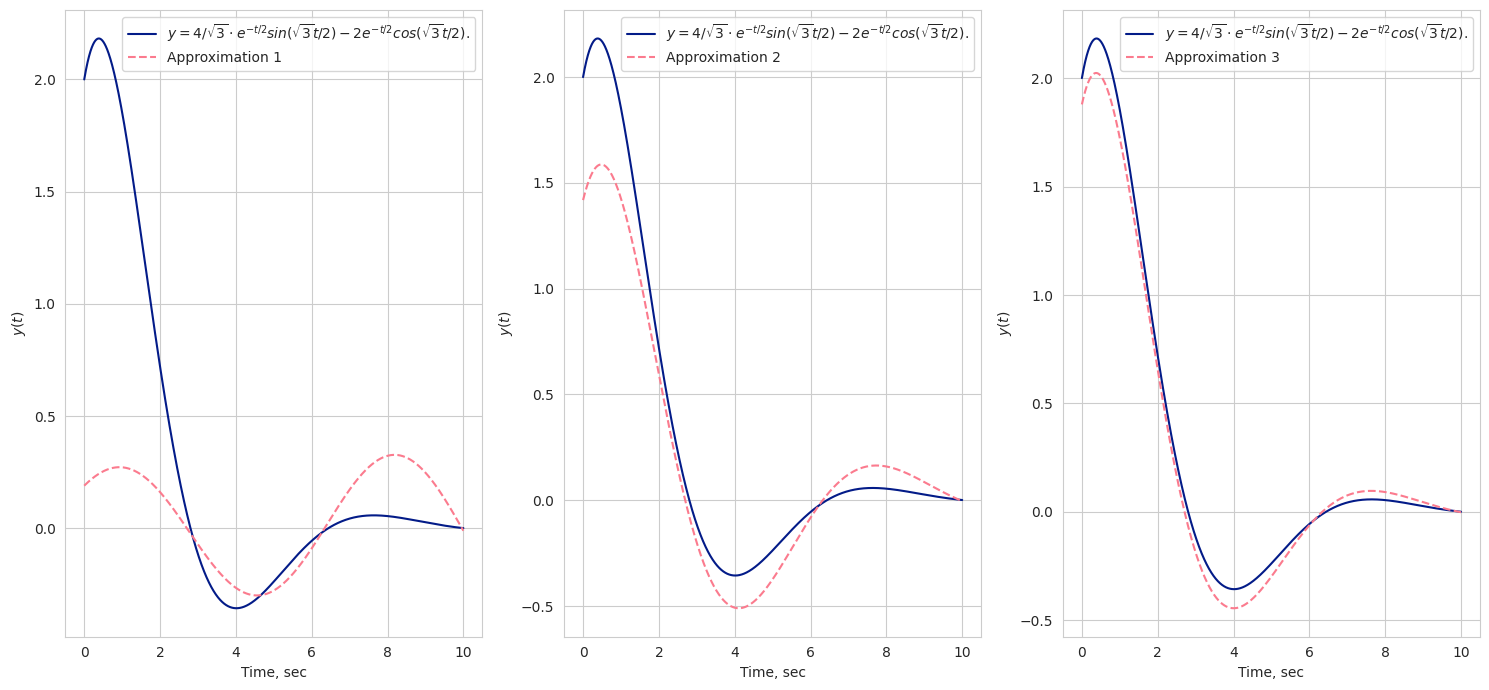
Дополнительно

Как вы могли заметить у нас не все параметры в модели обучаемыми. Коэффициент $\beta$ что должен был стоять в периодических функциях был сразу же зафиксирован. Зачем это было сделано? Показываю.

Объясняю. Косинус и синус, которые стоят в нашей аппроксимирующей модели

$y(t)=C_1\cdot e^{\alpha\cdot t} \cdot \sin(\beta t)+ C_2 \cdot e^{\alpha\cdot t} \cdot \cos(\beta t)$

очень сильно изменяют форму лосс функции над пространством параметров, делая ее более неприятной для методов градиентного спуска (практически всех оптимизаторов). Это связано с их периодическим характером и быстрыми изменениями, которые могут приводить к локальным минимумам и плохой сходимости алгоритмов оптимизации.

Наша модель сошлась к таким значениям

$\alpha=-0.79,\quad \beta=0.0,\quad C_1=0.0,\quad C_2=3.00$

То есть буквально модель приняла вид $y(t)=3e^{-0.79t}$ , что далека от нами задуманной.

Послесловие

Надеюсь вам было легко читать этот материал. Полный код вы можете найти на кагле, а меня в телеграме. Буду рад поправкам и комментариям.