Как я на спор развернул двусвязный список за O(1)
Как-то раз я случайно увидел, как мой коллега решает джуниорскую задачку разворачивания двусвязного списка на C++. И в тот момент странным мне показалось не то, что он лид и давно перерос подобное, а само решение.
Вернее, не так.
Решение было стандартным: тот же линейный проход с заменой указателей в каждом узле, как и писали сотни тысяч людей до него. Ничего необычного или сложного, но при взгляде на него у меня возникло два вопроса:
- Почему по умолчанию все решают задачу именно так?
- Можно ли сделать лучше?
Вкратце о матчасти. Если вы знаете, что такое двусвязный список, следующий абзац можно пропустить.
Двусвязный список ― одна из базовых структур данных, знакомство с ней обычно происходит на ранних этапах обучения программированию. Это коллекция, состоящая из последовательности узлов, которые содержат некие данные и попарно связаны друг с другом ― то есть, если узел A ссылается на B как на следующий, то узел B ссылается на A как на предыдущий. На практике вы можете встретить эту структуру в таких контейнерах, как std: list в C++, LinkedList в C# и Java. Скорее всего, вы найдёте её реализацию в стандартной библиотеке любого другого языка.
Далее в тексте будут описаны основные свойства и операции над таким списком с указанием вычислительной сложности.
Теперь вернёмся к озвученным ранее вопросам.
Я заглянул в условие задачи и увидел ответ на первый. Вот он:
struct node
{
int data;
node* next;
node* prev;
};
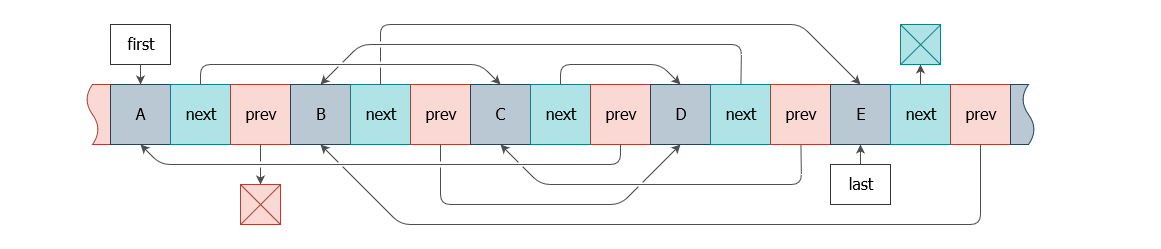
Эта структура уже была в самом условии. Не видите проблемы? Тогда посмотрите на схему:

Объясню. Код структуры узла выше ― некий канон, который повторяет схему на изображении. Мало кто сомневается, что эта структура должна существовать и выглядеть именно так в любой реализации этого списка, с поправкой на синтаксис языка и кодстайл.
Попробуйте в таких условиях получить список EBDCA. Линейный разворот всего списка тут ― решение очевидное и логичное, других вариантов нет. На первый взгляд.
Несколько минут я думал над ответом на вопрос, так ли это, и во время рабочего перерыва вбросил, что смогу выдать решение, у которого будет разворот за O (1), а результатом всё ещё останется двусвязный список. Спорили всей командой за обедом, мне никто не поверил. К тому времени я уже всё придумал, нужно было только расписать.
Вместо схемы и навязанного лейаута узла я решил отталкиваться от самих свойств структуры данных. Всё, что вы ожидаете от двусвязного списка, можно описать так:
- Список состоит из узлов, с каждым из которых связаны данные.
- Каждый узел связан с предыдущим узлом. Если такой связи нет, то это начальный узел списка.
- Каждый узел связан со следующим узлом. Если такой связи нет, то это конечный узел списка.
- Можно получить начальный и конечный узлы списка за константное время.
- Можно вставить и удалить узлы (из/в середину/начало/конец) за константное время.
- За константное же время можно получить следующий/предыдущей узел для исходного или убедиться, что такого нет и мы у границы коллекции.
- Как следствие предыдущего пункта — можно обойти список в любую сторону. За линейное время, разумеется.
Ключевой элемент здесь ― связи. А связь ― это не всегда указатель/ссылка в прямом смысле. Реализация должна позволять получать связанные данные и информацию о соседях узла, и совсем не обязательно в виде полей какого-то экземпляра. Более того, каноничный лейаут может даже вредить производительности. Например, во время прямого прохода по списку в классической реализации процессору на каждом шаге приходится подгружать в кэш-линии все поля узла, и существует совсем небольшая вероятность того, что соседние узлы окажутся в одной линии, даже если вы используете какой-то особый аллокатор.
»Что? Какие кэш-линии? » ― спросите вы:»Я кликнул почитать про разворот списка! »
Краткое отступление, чтобы вы не потеряли нить к этому моменту, узнав о такой заботе по отношению к каким-то там кэш-линиям с моей стороны. Я занимаюсь разработкой игр, поэтому у меня профдеформация: я пытаюсь оптимизировать всё, что плохо лежит. В последнее время я стараюсь следовать принципам Data-Oriented Design: это не название секты, а набор рекомендаций, помогающих машинам эффективнее справляться с задачами, которые мы перед ними ставим. На Хабре статьи по теме можно найти по тегу DOD. И соблюдение этих правил действительно даёт плоды. Это тема для отдельной статьи, или серии статей, или даже книги.
Дело в том, что в первое мгновение я даже не думал об эффективности разворота списка, когда смотрел на решение коллеги. Я думал об оптимизации всего лейаута коллекции. А константный разворот оказался интересным побочным продуктом.
Итак, можно повысить вероятность попадания соседних узлов в одну кэш-линию, упаковав их в один блок памяти. В таком случае вставлять новые узлы нужно в конец или любое другое свободное место, так как при удалении будут возникать «дырки» в блоке. Но тут есть свои проблемы:
- Любая операция вставки/удаления потенциально делает недействительным полученный ранее экземпляр узла, так как указатели на соседние узлы могут измениться.
- Даже если при обходе в кэш-линию попадут нужные узлы, рядом вы обнаружите поля с данными и поля с обратным указателем. Обратные указатели бесполезны при обходе и просто занимают ценнейшее пространство кэш-линии.
Да, часть проблем можно решить. Заменить указатели на индексы, например. Но лейаут остаётся прежним, и из-за этого всё ещё нельзя развернуть список за O (1), а это моя основная цель.
Тогда я решил пойти ещё дальше ― использовать структуру массивов (SoA) вместо массива структур (AoS), как было в предыдущем шаге. Получим представление примерно как на схеме:
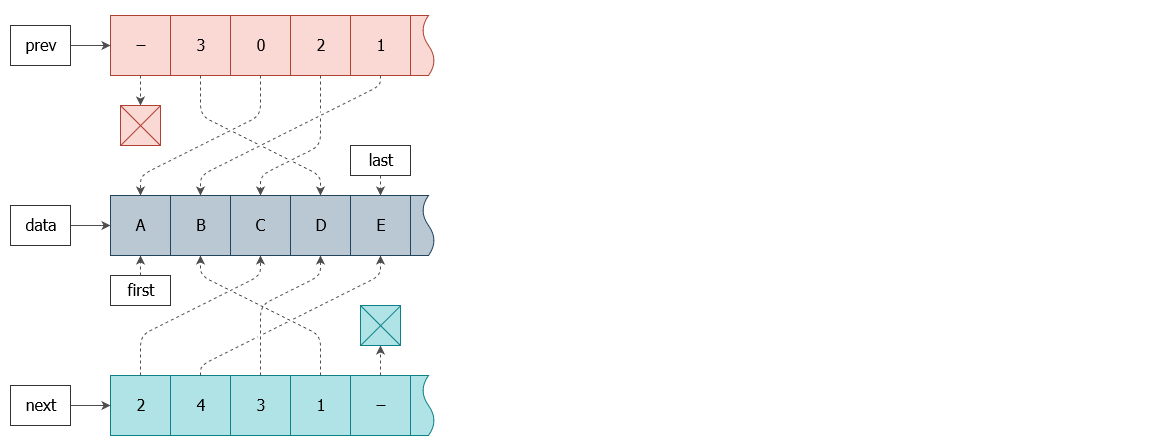
Что вам это даст? А вот что:
Узел ― это просто индекс в массиве. Его данные можно получить из data, а соседей из prev/next.
После вставки/удаления мы всё ещё имеем возможность продолжить работу с ранее полученным узлом-индексом.
Во время прохода процессор будет погружать только те данные, которые для этого прохода нужны ― то есть, prev или next в зависимости от направления. Вероятность более эффективной утилизации кэш-линии сильно повышается. А для не перемешанных участков списка она будет стопроцентной.
И знаете ещё, что?
На схеме выше изображён список ACDBE. Теперь взгляните на схему для EBDCA, в которой массив данных остаётся прежним:
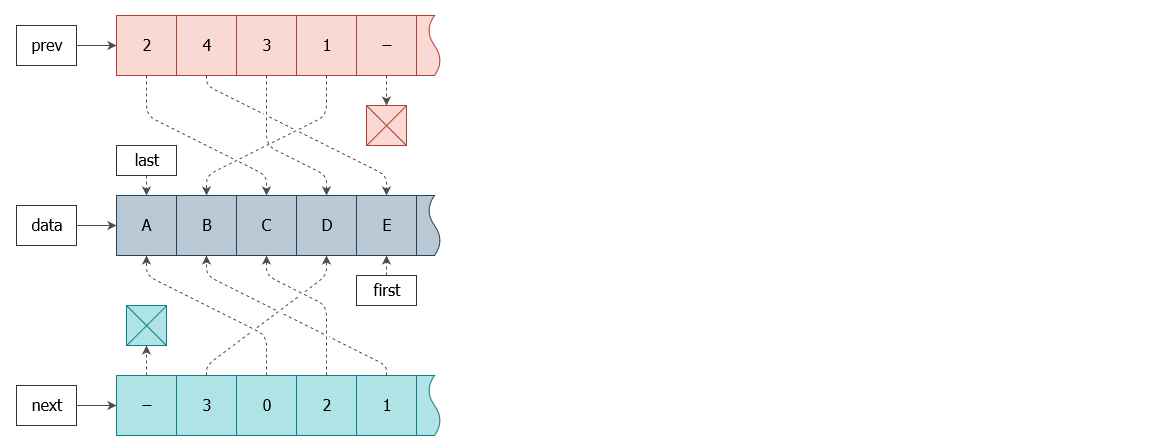
Как симметрично! Если вы думаете, что я специально подобрал такой список, чтобы всё работало, как надо, можете попробовать повторить те же операции на любой другой последовательности.
Итак, если мы будем хранить prev и next в виде указателей на блоки индексов, а first и last в виде самих индексов, что никто нам не запрещает делать, то операция разворота списка превратится в простой обмен значениями в следующих парах:
prev <-> next
last <-> first
Я не стал заморачиваться с менеджментом памяти, сделал всё на стеке. Также отсутствуют операции удаления узлов и проверки. Демонстрации работы кода это не помешает. Если кому-то будет нужно, этот кто-то может реализовать всё это под себя без особых проблем.
Итак, что в итоге получилось, без купюр и причёсывания:
template
struct doubly_linked_list
{
struct node { size_t index; };
// API получения данных и соседей для узлов
T& get(node n) { return data_[n.index]; }
const T& get(node n) const { return data_[n.index]; }
node first() const { return { first_ }; }
node last() const { return { last_ }; }
node next(node n) const { return { next_[n.index] }; }
node prev(node n) const { return { prev_[n.index] }; }
bool is_valid(node n) const { return n.index < length_; }
// Алгоритмы добавления и вставки от смены лейаута сильно не пострадали
node add(T v)
{
auto index = length_;
if (length_ == 0) first_ = 0;
data_[index] = v;
next_[index] = INVALID_INDEX;
prev_[index] = last_;
next_[last_] = index;
last_ = index;
length_++;
return { index };
}
node insert_before(T v, node n)
{
auto index = length_;
data_[index] = v;
next_[index] = n.index;
auto prev = prev_[index] = prev_[n.index];
prev_[n.index] = index;
next_[prev] = index;
length_++;
if (n.index == first_) first_ = index;
return { index };
}
// …тут должны быть методы удаления, они не сильно будут отличаться от псевдокода в любом туториале,
// разве что придётся вести учёт «дырок» в отдельном массиве. Это также затронет и add/insert_before -
// там вместо length_ нужно будет забирать первую «дырку».
// Вишенка на торте – то, ради чего всё это было сделано:
void reverse()
{
std::swap(first_, last_);
std::swap(next_, prev_);
}
private:
static constexpr size_t INVALID_INDEX = SIZE_T_MAX;
T data_[Cap];
size_t indirection_[Cap * 2];
size_t *next_ = indirection_;
size_t *prev_ = indirection_ + Cap;
size_t first_ = INVALID_INDEX;
size_t last_ = INVALID_INDEX;
size_t length_ = 0;
};
Тестовый запуск показал успех:
auto list = doubly_linked_list();
auto pos = list.add(0);
for (int i = 0; i < 5; ++i) pos = list.insert_before(i + 1, pos);
std::cout << "list";
for (auto n = list.first(); list.is_valid(n); n = list.next(n))
std::cout << list.get(n) << " ";
// > list 5 4 3 2 1 0
list.reverse();
std::cout << std::endl << "reversed";
for (auto n = list.first(); list.is_valid(n); n = list.next(n))
std::cout << list.get(n) << " ";
// > reversed 0 1 2 3 4 5
На самом деле, я соврал о том, что при AoS лейауте нельзя было развернуть список так же эффективно. Можно провернуть подобный трюк и там, но уже если захотите поупражняться сами: от лишних данных в кэш-линиях это всё равно не спасёт, поэтому я не стал этим заниматься.
Для меня решение задачи с разворотом было всего лишь челленджем, так что я не планирую развивать эту реализацию в будущем. Может быть, кто-то найдёт в этом практическую пользу и сделает что-то хорошее для себя и других ― например, cache-friendly дэк или оптимальную реализацию DCEL, который можно мгновенно вывернуть наизнанку. Словом, следуйте своему воображению.
А теперь к выводам:
Для объяснения своих идей друг другу мы часто используем схемы. Это неплохо и зачастую действительно удобнее. Но иногда мы становимся заложниками такого изложения идей. В случае с двусвязным списком проблема не в схеме ― она всё ещё хороша в академическом смысле, как и классический лейаут. Проблема в том, что эту схему, как и любую другую, часто понимают буквально — как постулат, а не как одну из концепций.
В качестве второго вывода приведу базовый постулат Data-Oriented Design: знайте свои данные и то, что вы собираетесь с ними делать. Это действительно помогает повысить эффективность ваших решений. Пример с двусвязным списком и его разворотом — это всего лишь игрушка, зарядка для ума. Попробуйте взглянуть на свои решения с подобной точки зрения и обнаружите очень много интересных ходов, о которых раньше даже и не думали.
Вот и всё. И поменьше вам кэш-миссов в новом году.
