Измерение и формирование частотных характеристик электрогитар
Поговорим об искусстве. Например, о музыке. Например, о гитарах.
Создание электрогитар вещь достаточно консервативная. Несмотря на огромные успехи в обработке сигналов, которые позволяют доставать из гитар любые звуки в реальном времени (JTV89), до сих пор достаточно ценится тот самый «теплый и ламповый» звук, которым гитара должна обладать сама по себе. С другой стороны, при этом всем, звук гитары должен обладать именно теми характеристиками, которые хочет заказчик, которому вдруг захотелось иметь какой-то специфический звук у своей гитары.

Звук гитары формируется следующими вещами:
- Положением звукоснимателей
- Характеристиками звукоснимателей
- Типом струн
- Резонансными свойствами корпуса и материалов
За те струны, которыми будет пользоваться человек, создатель гитары, конечно, не отвечает. Влияние корпусных частей на звук для электрогитар (не полуакустических) штука достаточно религиозная. Влияние этого, с одной стороны не отрицается, но с другой стороны никто толком не знает, как это учитывать (а даже если говорит, что знает, скорее всего ничего толком объяснить не сможет).
Остаются звукосниматели. Их положение и характеристики передачи сигнала. Это мы можем померить, сравнить и учесть. По этим вопросам существует достаточно разработанная и несложная теоретическая база.
Теоретическая часть
Теоретические основы, позволяющие оценить влияние положения датчика, можно найти тут. А простенькое теоретическое описание передаточных характеристик датчика тут. Я со своей стороны, постараюсь как можно короче это все пересказать, чтобы вам по английски не читать.
Струна гитары это веревочка, которая привязана с двух концов. Когда мы ее дергаем, она начинает вибрировать, потому что она привязана и никуда ей не сбежать. Но есть важные аспекты того, как именно это происходит. Струна вибрирует с различными периодами. Периодами кратными длине струны: 1, ½, ¼, ⅛, … Это можно изобразить такой картинкой:
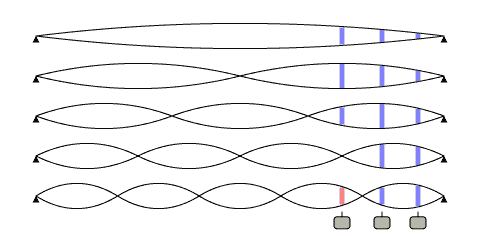 Гармоники струны. Картинка из www.till.com/articles/PickupResponse |
 |
Можно самому провести эксперимент с гитарой, внимательно посмотрев на картинку. Дернуть за струну, а потом легонько пальцем прикоснуться ровно в середине струны. Как можно понять из картинки, такое движение заглушит все нечетные гармоники у которых в этом месте не минимум, и звук не пропадет, а несколько изменится. Такой прием называется натуральный флажолет, если дернуть за струну уже держа палец в середине и тэппинговый флажолет, если дернуть за струну, а потом прикоснуться пальцем. Но это лирика. Нам важно, что частот много и, на самом деле, все не ограничивается только периодами кратными длине струны.
И тут нам надо вспомнить, что звукосниматель создает магнитное поле в районе струны. Металлическая струна колеблется в этом поле прямо над датчиком и возмущает его как-то. За счет этого в контуре датчика образуется ток в соответствии с законом Фарадея. И всякие скорости движения струны непосредственно над датчиком нам и интересны.
Физики установили, что относительная (нормированная) скорость движения струны над каким-то местом струны описывается такой формулой:
X — это расстояние от порожка (нижнего) до звукоснимателя, L — длина вибрирующей части струны (тут есть некоторые оговорки, но мы их опустим).
Примечание о расстоянии X. Если бы струна колебалась только с одной основной гармоникой, максимум этой величины приходился бы ровно на центр струны (синус пи пополам равен 1)
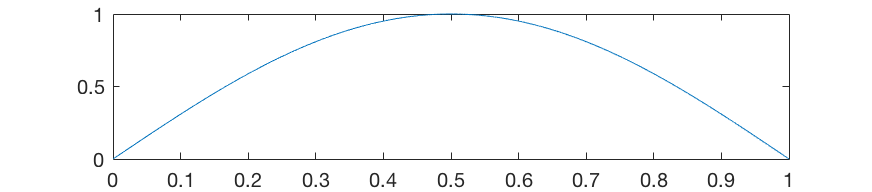
Однако, струна имеет и остальные гармоники, и интенсивность гармоник падает пропорционально квадрату их номера, вторая — в четыре раза слабее, третья — в девять, и так далее. Даже добавление второй гармоники изменит скорость струны и сделает её распределение несимметричным:
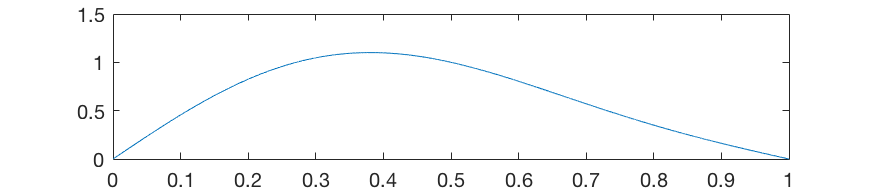
А если просуммировать «все» гармоники, максимум сдвинется в положение, находящееся ровно в ⅓ от порожка.
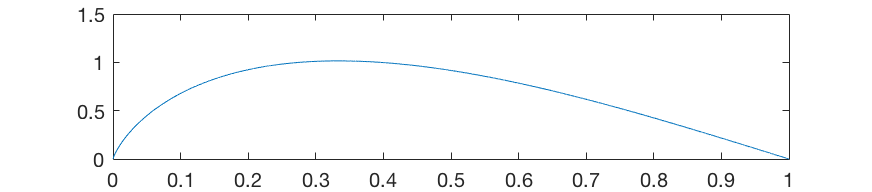
Этот факт и определяет положение датчиков и резонаторного отверстия на корпусе гитары.
И обратно к теме. У каждой струны есть своя основная частота F0, и основная длина струны L0. Очевидно, что изменения частоты при изменении звучащей «длины» будут обратно пропорциональны относительно основных частот (чем больше длина, тем меньше частота):
Можно это взять и подставить в уравнение 1.
Здесь — константа, при условии, что датчик стоит над одним местом струны, и получается, что скорость синусоидально зависит от частоты. Естественно, знак скорости нас не интересует, поэтому можно нарисовать эту зависимость в децибелах, как в вышеуказанной статье:
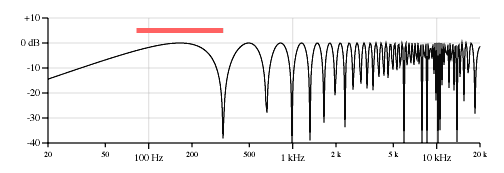
Теоретическая ЧХ «восприятия» струны датчиком с нулевой шириной. Картинка отсюда
В логарифмическом масштабе частот график амплитуды синуса выглядит изрядно загадочно и необычно… Но зато из формулы (2) очевидно, что при изменении X, вся эта картинка будет сдвигаться вправо/влево относительно оси частот. Это, собственно, и формирует характерные звуки bridge и neck датчиков (тут есть картинка, как это расположено). Для bridge первый пик уезжает вправо, для neck влево. Для bridge X совсем маленький, соответственно F должен быть сильно больше, чтобы достичь первого пика. Таким образом для bridge характерно менее басовое звучание и больше средних частот.
На этом можно было бы остановиться с положением датчика, но это еще не все.
Датчик — это не точка над гитарой, из которой берется звук. У датчика есть ширина. Т.е. Датчик «собирает» и складывает звук над «набором» точек над собой, для каждой из которых частотная характеристика немного сдвинутая. Или умными словами — берется интеграл по всей длине пересечения датчика и струны (сюда тем, кто интегралов не боится). И из этого интеграла у нас получается, что у нас уже не один синус, а два. Оба зависят от частоты и один зависит от X, а другой от ширины датчика W.
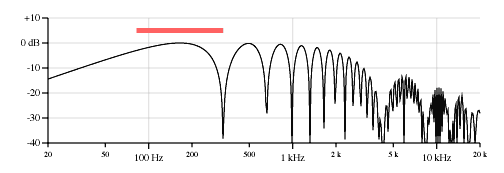
Теоретическая ЧХ «восприятия» струны датчиком с конечной шириной. Картинка из http://www.till.com/articles/PickupResponse/
Примерно так это выглядит математически:
где, k — константа, зависящая от струны. Понятно, что W (иногда намного) меньше X даже с учетом деления на 2, поэтому у графика появляется еще один пик, который сдвигается сильно в область высоких частот.
И тут у нас образуются какие-то нехорошие дыры в частотной характеристике (ЧХ) в самых неприятных местах. Если мы будем расширять W, у нас с одной стороны дыры в ЧХ будут пропадать, зато и амплитуда сигнала будет уменьшаться, потому что в формуле (3) в знаменателе стоит W. В общем, есть некоторая проблема, которая, как ни странно, решается автоматически.
Мы много говорили о том, где датчик стоит. Но очень мало о том, как он проводит сигнал. Датчик это RLC-цепь второго порядка с резонансом и его ЧХ выглядит примерно так:
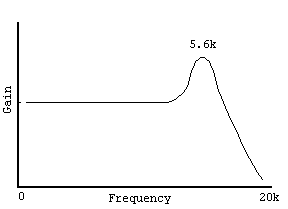
ЧХ типичного датчика как резонансной цепи второго порядка. Картинка из www.muzique.com/lab/pickups.htm
Резонансный пик достаточно изящно покрывает часть дырок, образованных тем фактом, что датчика есть ширина. И все искусство создания гитары состоит в том, чтобы ни в каких нотах особенно не было провалов в громкости, и были пики в нужных местах. В данной статье, правда, мы про это ничего не будем говорить особо. Это измерить можно, например, так.
А теперь, когда вы примерно понимаете, что происходит, собственно, расскажем, что мы измеряли и что получили.
Установка и алгоритм обработки
Нам было интересно узнать, а чем звук выходящий из гитары отличается от того, который звучит, когда дергаешь за струну.
Два слова про установку и измерение
Чтобы это определить, мы брали микрофон Shure M58. В силу его популярности, везде валяется его примерная частотная характеристика. Таким образом мы могли измерить «реальное звучание» (которое и определяется струной и корпусом). Далее ставили микрофон напротив датчика (на оптимальном расстоянии для записи). Дергали за струну. В микрофон записывалось то, что определено пунктами (3,4) из первой части, а в датчик всеми четырьмя. Далее остается только как-то «вычесть» из звука записанного из датчика звук записанный с микрофона и посмотреть, что собственно датчик со звуком делает, в отрыве собственно от того, какой это звук, из чего сделана гитара, и какие на ней струны. Мы написали программу, которая умеет это все делать и строить всякие графики.
На самом деле все не так просто, но про это в конце.
Какие устройства и ПО, повторим еще раз?
- Звуковая карта EMU 0204
- Микрофон Shure M58
- Fender Stratocaster Ritchie Blackmore Edition
- мастеровая копия Music Man JP7
- Программа для автоматической обработки сигнала на C# (NAudio, MathNet)
- Дополнительный анализ: Excel, Matlab
Алгоритм
- В левый канал мы записываем микрофон, в правый в линию включаем гитару (EMU такое позволяет).
- Дергаем за одну струну N раз, чтобы «одинаковые» сигналы записались в датчик и микрофон и было что усреднять. Следим, чтобы между нотами были промежутки тишины.
- Убираем шум и немного выравниваем сигналы на глаз (но это не обязательно)
- Выделяем из записи каждую отдельную записанную ноту в два массива: нота с микрофона, нота с датчика.
- Нормируем все массивы с записями, чтобы ноты имели одинаковую «мощность на единицу времени»
- Для каждого массива делаем фурье преобразование N= 32768 (но можно другое, 16384, тоже ничего)
- Выделяем в спектрах массивов пики, которые соответствуют, собственно звуку ноты и сглаживаем (Как ни странно, именно сама нота нам особо и не помогает в оценках)
- Вычитаем из каждого спектра датичка каждый спектр микрофона (учитывая собственную ЧХ микрофона).
- Усредняем результаты для всех частот, получая спектр, характеризующий отличие звука с датчика от звука записанного на микрофон.
Немного пройдемся по некоторым частям процесса.
Выделение значимых частей из записи
Выделение происходит по крайне простому принципу: Где у нас сигнал в среднем больше некоторого граничного значения на протяжении достаточно большого количества времени, то у нас и нота.
Для этого мы:
- Берем абсолютные значения сигнала датчика;
- Прибавляем константу C (чтобы нуля не было, потому что потом надо логарифмировать);
- Переводим в децибелы;
- Сглаживаем скользящим средним;
- Проходим по всему массиву, выделяя куски, где сигнал больше некоторой константы Lim;
- Откидываем слишком короткие куски;
- Считаем, что сигнал у датчика находится там же где у микрофона, поэтому сигнал для микрофона обрезаем по тем же границам.
- Возвращаем два массива, содержащих «нарезки» нот.
Нормировка
Все ноты записаны с разной громкостью и громкость с микрофона и с датчика различаются. Поэтому теперь надо это все выровнять, чтобы иметь возможность сравнивать. Для этого мы:
- Берем референсный «обрезок» и для него считаем «мощность на единицу времени»:
Где, N — размер i-го массива, r — значения из i-го массива.
- Потом для каждого i-го «обрезка» пересчитываем значения массива:
Гармоники
После того, как каждый из обрезков нормируется, от него берется фурье и вычисляется его спектр. В спектре очень много лишнего, от которого надо избавиться. Например, собственно, сыгранная нота, которая имеет большие, но сильно варьирующиеся, амплитуды. Для этого мы для начала все эти пики находим. Как?
- Для всего спектра делаем двойное сглаживание скользящим средним с коэффициентом 0.05.
- Сглаживание делает ряд запаздывающим относительно оригинального, потому что в скользящем среднем большое значение начинает иметь «предыстория» любой точки. Чтобы этого избежать, находится смещение, проверкой корреляции оригинального ряда и сглаженного. Выбирается такое смещение, которое делает эту корреляцию максимальной.
- После этого находятся непрерывные массивы точек, которые превышают сглаженный и сдвинутый график на 1.5 СКО оригинального ряда и из них берется максимальная. Это выглядит примерно так:
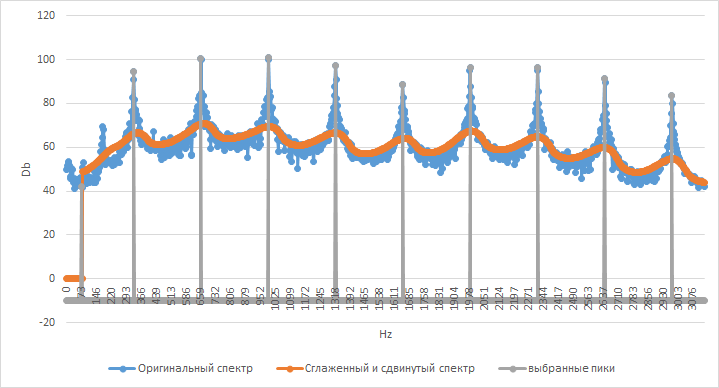
Спектр ноты Ми первой октавы и то, как он сглаживается
Далее, относительно каждого пика мы заменяем ±M точек оригинального ряда на точки сглаженного и сдвинутого ряда. В принципе, можно было сразу брать сглаженный, но мало ли что-то важное можно пропустить.
Таким образом, мы получаем ряды «без пиков» как для микрофона, так и для датчика.
Получение частотной характеристики
Вычитая друг из друга полученные ряды датчика и микрофона и далее усредняя, мы получаем что-то такое:
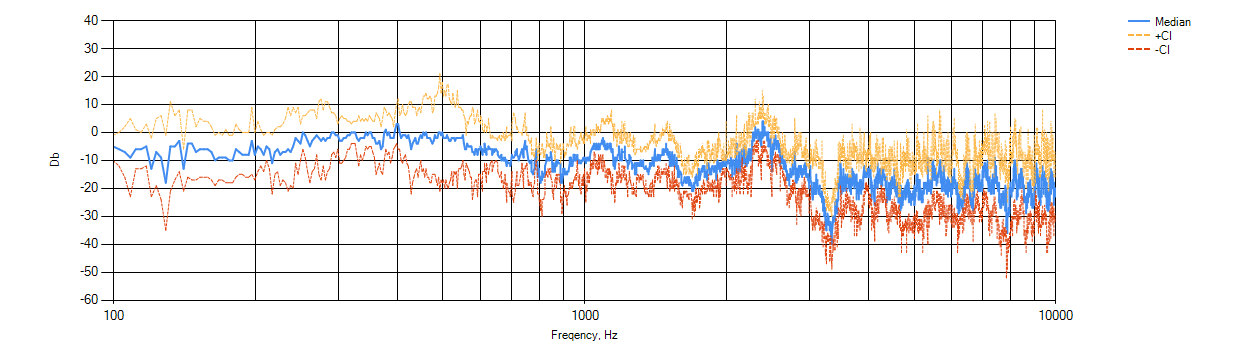
ЧХ Neck датчика копии JP7 (в некотором смысле передаточная функция датчика).
CI+, CI- это плюс/минут доверительный интервал для усредненного ряда. Важно тут понимать, что конкретные значения децибел тут не так важны, как относительное расположение. Мы не знаем какая «на самом деле» была громкость струны. Микрофон мог стоять дальше, мог ближе. Нормирование громкостей сделало громкости интегрально схожими, но мы не знаем, были ли они такими на самом деле. Поэтому подпись оси Y во многом просто потому что не подписывать оси некрасиво. Никакого сакраментального смысла ось Y не несет. Однако иногда бывает интересно посмотреть, как соотносятся сигнал микрофона и датчика, когда они нарисованы отдельно:
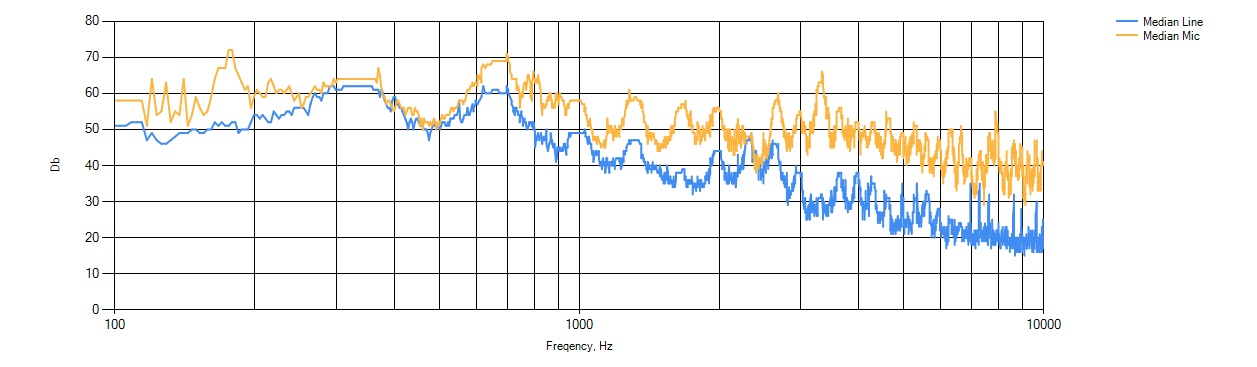
Сглаженные спектры для Neck датчика копии JP7. Спектры нарисованы усредненными и сглаженными.
Но опять таки надо помнить, что эти графики можно смело двигать друг относительно друга вверх и вниз.
Вернемся к теории
А зачем собственно нужна была вся эта теория перед графиками? Как эти вещи связаны? Вот тут-то и заключается самое интересное.
Давайте рассмотрим ЧХ для JP7 и такую же теоретическую, рассчитанную для длины грифа 650 мм, расстояния датчика от нижнего порожка 130 мм (neck), шириной датчика 2 дюйма (51 мм), и для Ми первой октавы 328 Гц:
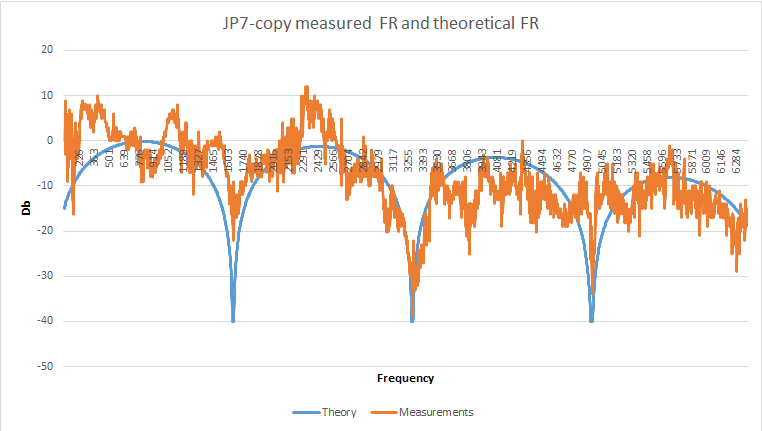
Мы явно видим, как с теоретическими совпадают провалы, связанные с расположением датчика. sin (pi*129.5×1620/(640×328)) примерно равен 0 и это половина периода, ровно как на графике. В районе 4800 Гц провал меньше, потому что именно там находится (скорее всего) резонанс передаточной функции электрической части датчика.
Не всегда оно так очевидно.
Возьмем другую гитару. Fender Stratocaster Ritchie Blackmore Edition. Достаточно характерная гитара со специфическими свойствами и датчиками со сложным названием Seymour Duncan Quarter Pound Flat SSL-4 single-coil Strat pickup. Рассмотрим ее полученную частотную характеристику. Длины грифа 655 мм, расстояния датчика от нижнего порожка 150 мм (neck), шириной датчика 2 дюйм (50 мм) (на самом деле, там стоит очень-очень мощный сингл, и параметры хамбакера для него подходят лучше), и для Ми первой октавы 328 Гц:
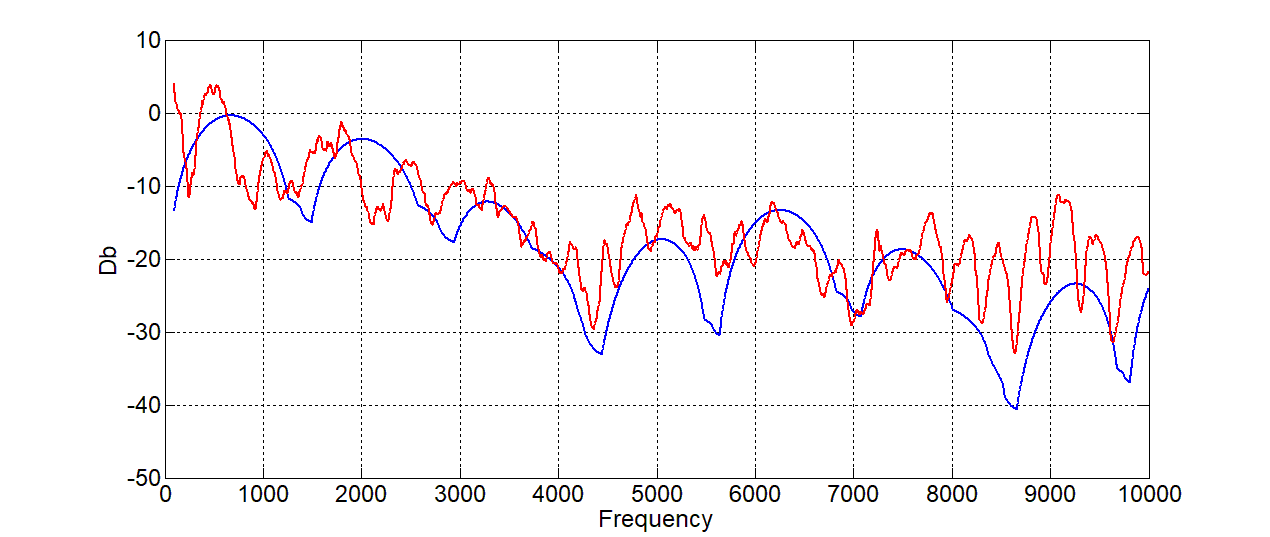
Надо сказать, что так получилось не сразу, а при наложении фильтра низких частот на теорию. И в целом видно влияние каких-то других странных вещей.
А что еще можно сравнить?
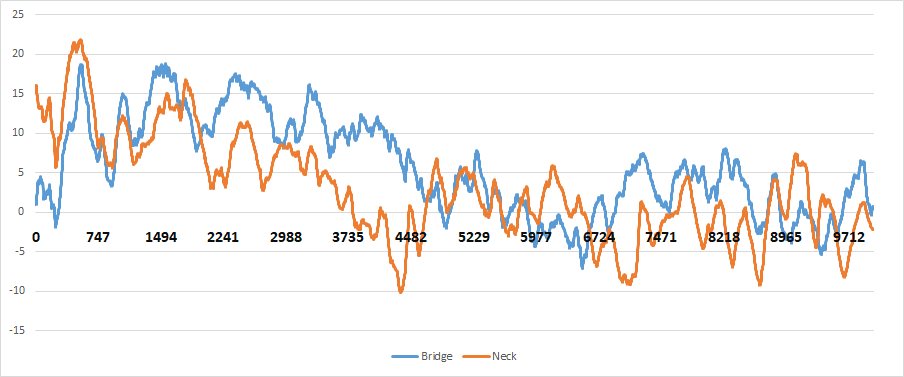
Посмотрим на тот же фендер. Еще можно сравнить, например, neck (150 мм) датчик c bridge (50 мм) датчиком. Измеряем характеристику первого, характеристику второго, потом смотрим на отдельном графике (после небольшой фильтрации).
Зеленым на графике — bridge, оранжевым — neck. Из графика видно ровно то, что и так все вроде как знают. Neck вытаскивает совсем низкие частоты, Bridge средне-высокие. Вопросы тут, как обычно, возникают в деталях, которые интересны только большим любителям музыки и всего этого. Например, в пиках neck в районе 9000 Гц.
Оговорки
Теперь про то, почему «на самом деле все не так просто».
Микрофон, особенно направленный, снимает тоже только часть струны, как и датчик, соответственно, имеет сходную ЧХ, зависящую от положения микрофона и «ширину» захвата звука. Однако, очевидно, что у микрофона «ширина» датчика намного больше, соответственно, все частоты синуса намного больше и ЧХ микрофона во многом выражается в виде высокочастотных колебаний, «зашумляющих» спектр.
Возьмем, например, частотную характеристику Fender Stratocaster Ritchie Blackmore Edition, измеренную для neck положения датчика. Поскольку ЧХ описывается синусом (как мы это знаем из теории), можно еще раз взять от спектра фурье преобразование, чтобы оценить выделяющиеся частоты (брать фурье от спектра весьма сомнительное развлечение, кстати). Результат представлен на картинке.
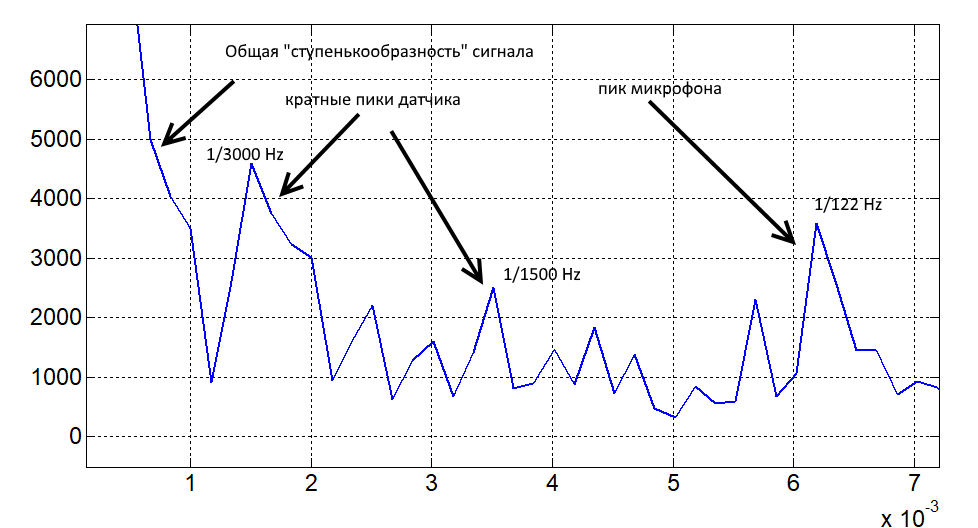
Фурье преобразование спектра Fender Stratocaster Ritchie Blackmore Edition (neck)
Четко выделяются пики, определенные свойствами «положения датчика», «ширины датчика» и «ширины микрофона». Скорее всего нет сильно выделенного пика «положения микрофона», потому что микрофон стоял прямо напротив датчика…
Выводы для тех, кто любит выводы
- Положение датчика влияет не менее, чем его собственная частотная характеристика. А может даже и больше;
- Ширина датчика, исходя из формулы (3), влияет ровно как указано на картинке.
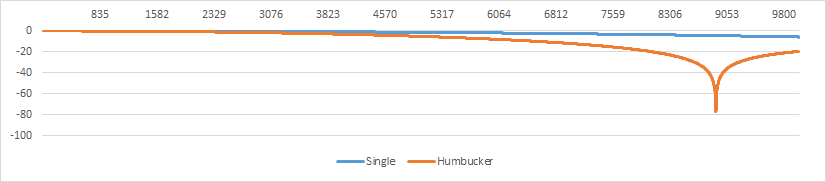
Для сингла она не влияет ровно никак. Для хамбакера все сделано так, что в районе 9000 находится провал. И это тоже формирует фирменный «не яркий» звук такого звукоснимателя. Хотя, конечно, это не единственная вещь, влияющая на звук такого датчика;
- Невозможно поставить датчик так (или сделать его такой ширины), чтобы он не убивал какие-то частоты. Собственно эти убитые частоты и задают характерный звук гитары;
- Если вы хотите какой-то определённый звук от заказываемой гитары, важно найти, у кого вы этот звук слышали, тогда будет проще ориентироваться на положение датчиков на том инструменте.
- В принципе, можно запросто дерзать и теоретически строить какие-то свои фильтры из комбинаций положений, ширин и электрических схем датчиков. Накладывать эти фильтры на какой-нибудь записанный на микрофон звук и смотреть — нравится ли вам? Хотите ли вы, чтобы гитара звучала именно так? Готовы ли вы так искать идеальный звук?
Соавтор: А.А. Городецкий, Imperial College London.
