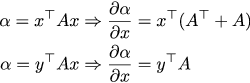Избранные главы теории управления на пальцах: линейные наблюдатели динамических систем
Продолжаю писать о теории управления «на пальцах». Для понимания текущего текста необходимо прочитать две предыдущие статьи:
- Методы наименьших квадратов
- Линейно-квадратичный регулятор, вводная
- Линейно-квадратичный регулятор и линейные наблюдатели
Я совсем не являюсь специалистом в теории управления, лишь читаю учебники. Моя задача — понять теорию и применить на практике. В этой статье только теория (ну, немножко сопутствующего кода), в следующей будем разговаривать о практике, маленький кусочек которой можно посмотреть тут:
Исправления и дополнения приветствуются. В сотый раз напоминаю, что в первую очередь я пишу эти тексты для самого себя, так как это меня заставляет структурировать знания в голове. Этот сайт является для меня своего рода публичной записной книжкой, к которой, к слову, я сам регулярно возвращаюсь. На всякий случай напомню хорошо описывающий мою жизнь бородатый анекдот:
Разговор двух преподавателей:
— Ну и группа мне в этом году попалась тупая!
— А что так?
— Представляешь себе, объясняю теорему — не понимают! Объясняю второй раз — не понимают! В третий раз объясняю, сам уже понял. А они не понимают…
Линейно-квадратичный регулятор, вид сбоку
LQR: Формулировка задачи
Итак, давайте вспомним то, о чём мы говорили в прошлой статье, а именно, о том, что в русской школе называют аналитическим конструированием оптимальных регуляторов. Я даже пример возьму из той статьи.
Пусть у нас есть некий автомобиль, состояние которого в данный момент времени k характеризуется его координатой x_k и скоростью v_k. Начинается эксперимент с некоего начального состояния (x_0, v_0), и наша задача остановить автомобиль в нуле координат. Воздействовать мы на него можем посредством газа/тормоза, то есть, через ускорение u_k. Запишем эту информацию в виде, который удобно передавать от человека к человеку, т.к. словесное описание громоздко и может допускать несколько тактовок:
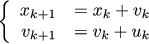
Ещё удобнее записать эту информацию в матричой форме, так как матрицы можно подставлять в эту формулировку самые разные, тем самым язык очень гибок и может описать множество разных проблем:
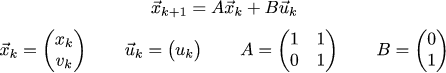
Итак, мы описали динамику системы, но мы не описали ни цели, ни что именно считать хорошим управлением. Давайте запишем следующую квадратичную функцию, которая берёт в качестве параметров траекторию автомобиля и последовательность управляющих сигналов:
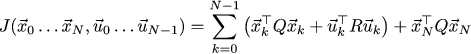
Мы стараемся найти такую траекторию автомобиля, которая минимизирует значение этой функции. Эта функция задаёт компромисс целей: мы хотим, чтобы система как можно быстрее сошлась к нулю, при этом сохранив разумную величину управления (не надо тормозить юзом!)
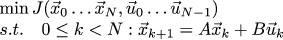
Итого у нас есть задача минимизации функции с линейным ограничением на входные переменные. Для конкретно нашей задачи про автомобиль в прошлый раз мы выбрали такие веса 1 и 256 для наших целей:
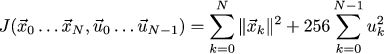
Если в начальный момент наш автомобиль находится в позиции 3.1 и имеет скорость полметра в секунду, то оптимальное управление выглядит следующим образом (цитирую картинку из прошлой статьи):
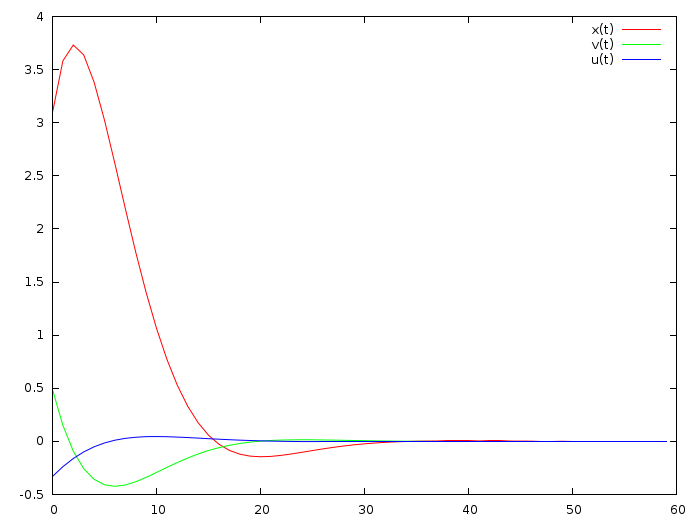
LQR: Решаем задачу
Попробуем нарисовать эти же кривые несколько другим способом, нежели в прошлый раз. Записывать суммы очень громоздко, давайте сведём к матричному виду. В первую очередь всю нашу траекторию и всю нашу последовательность управления сведём в здоровые матрицы-столбцы:
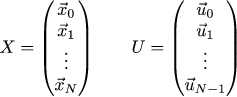
Тогда связь координат с управлением можно записать следующим образом:
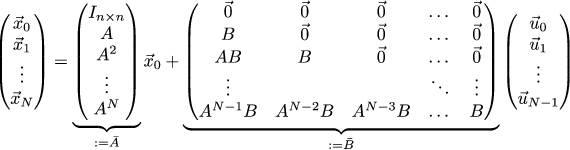
Или ещё более кратко:
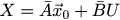
В этой статье палки над матрицами означают сведение мелких матриц, которые описывают одну итерацию, в крупные для всей задачи. Для конкретно нашей задачи степени матрицы A^n выглядят следующим образом:
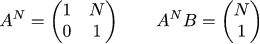
Для пущей наглядности давайте явно напишем Ā и B̄:

И даже приведу исходный код, который заполняет эти матрицы в numpy:
import matplotlib.pyplot as plt
import numpy as np
np.set_printoptions(precision=3,suppress=True,linewidth=128,threshold=100000)
def build_Abar(A, N):
n = A.shape[0]
Abar = np.matrix( np.zeros(((N+1)*n,n)) )
for i in range(N+1):
Abar[i*n:(i+1)*n,:] = A**i
return Abar
def build_Bbar(A, B, N):
(n,m) = B.shape
Bbar = np.matrix( np.zeros(((N+1)*n,N*m)) )
for i in range(N):
for j in range(N-i):
Bbar[(N-i)*n:(N-i+1)*n,(N-i-j-1)*m:(N-i-j)*m] = (A**j)*B
return Bbar
A = np.matrix([[1,1],[0,1]])
B = np.matrix([[0],[1]])
(n,m) = B.shape
N=60
Abar = build_Abar(A, N)
Bbar = build_Bbar(A, B, N)
Сведём в большие матрицы и коэффициенты нашей квадратичной формы:

В конкретно нашей задаче про автомобиль Q̄ — это единичная матрица, а R̄ — единичная, умноженная на скаляр 256. Тогда функция качества управления записывается в матричной форме очень кратко:
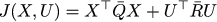
И мы ищем минимум этой функции с одним линейным ограничением:
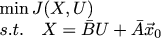
Заметка самому себе: отличный повод для того, чтобы разобраться с множителями Лагранжа, преобразование Лежандра и получаемой из этого функции Гамильтона. А также как из этого вытекает объясние LQR через динамическое программирование и уравнения Риккати. Видимо, ещё нужно писать статьи :)
Я ленив, поэтому в этот раз пойдём самым прямым путём. J зависит от двух аргументов, которые между собой линейно связаны. Вместо того, чтобы минимизировать функцию с линейными ограничениями, давайте просто из неё уберём лишние переменные, а именно заменим в ней вхождения X на Ā x_0 + B̄ U:
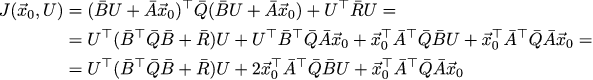
Это довольно нудный, но совершенно механический и не требующий головного мозга вывод. При переходе от предпоследней строчки к последней мы воспользовались тем, что Q̄ симметрична, это нам позволило написать Q̄ + Q̄ ^T = 2 Q̄.
Теперь нам нужно просто найти минимум квадратичной функции, никаких ограничений на переменные не накладывается. Вспоминаем десятый класс школы и приравниваем нулю частные производные.
Если вы умеете дифференцировать обычные многочлены, то умеете брать производные и от матричных. На всякий случай напомню правила дифференцирования:
Опять самую чуточку нудного написания закорючек и мы получаем нашу частную производную по вектору управления U (мы опять воспользовались симметричностью Q̄ и R̄):
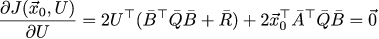
Тогда оптимальный вектор управления U* можно найти следующим образом:
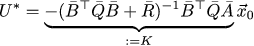
Ну и как же мы пишем закорючки, но до сих пор ещё ничего не нарисовали? Давайте исправляться!
K=-(Bbar.transpose()*Bbar+np.identity(N*m)*256).I*Bbar.transpose()*Abar
print("K = ",K)
X0=np.matrix([[3.1],[0.5]])
U=K*X0
X=Abar*X0 + Bbar*U
plt.plot(range(N+1), X[0::2], label="x(t)", color='red')
plt.plot(range(N+1), X[1::2], label="v(t)", color='green')
plt.plot(range(N), U, label="u(t)", color='blue')
plt.legend()
plt.show()
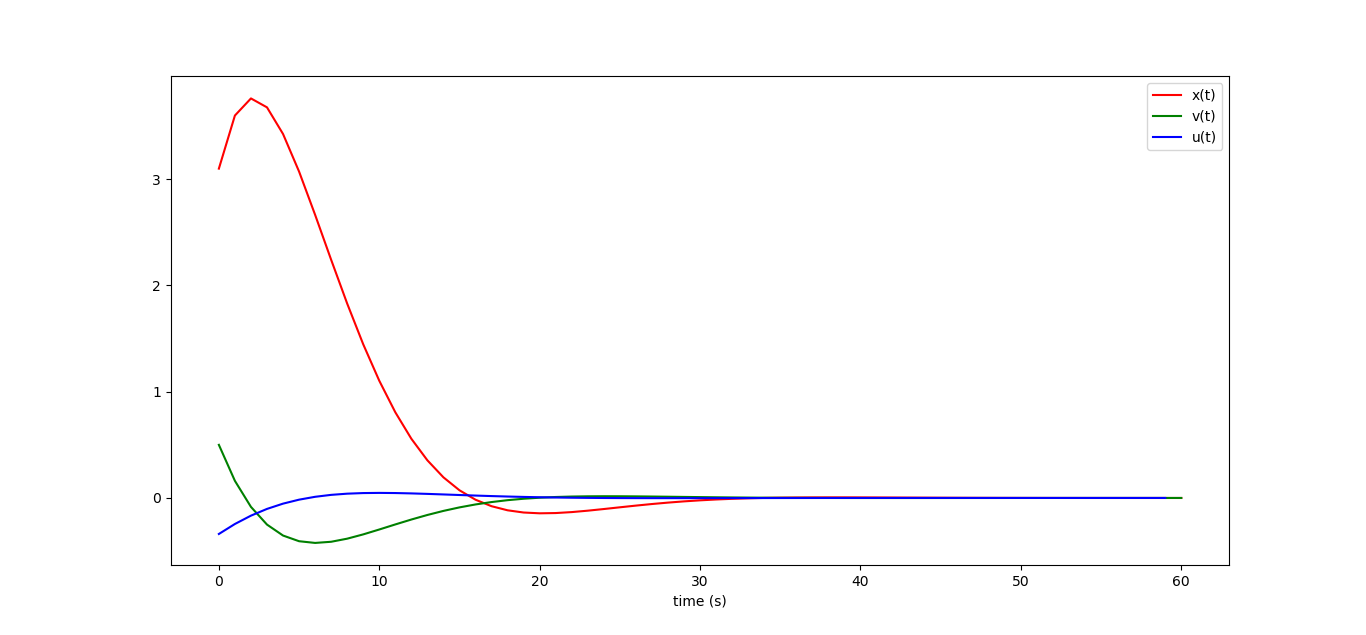
Это даст следующую картинку, обратите внимание, что она прекрасно совпадает с той, что мы получили в прошлой статье (рисовалка тут):
LQR: Анализ решения
Линейная связь управления и состояния системы
Итак, теория нам говорит о том, что (при далёком горизонте событий) оптимальное управление линейно зависит от оставшегося расстояния до конечной цели. В прошлый раз мы это доказали для одномерного случая, в двумерном поверив на слово. В этот раз опять строго доказывать не буду, оставив это для более позднего разговора о множителях Лагранжа. Тем не менее, интуитивно понятно, что так оно и есть. Ведь мы получили формулу U = K*x0, где матрица K не зависит от состояния системы, но только от структуры дифференциального уравнения (от матриц A и B).
То есть, u_0 = k_0*x_0. К слову сказать, k_0 мы получили равным [-0.052 -0.354]: K = [[-0.052 -0.354]
[-0.034 -0.281]
[-0.019 -0.215]
[-0.008 -0.158]
[ 0. -0.11 ]
...
Сравните этот результат с тем, что я получил при помощи МНК и с тем, который был получен решением уравнения Риккати (в комментариях к предыдущей статье). Интуитивно понятно, что если u0 зависит линейно от x_0, то при далёком горизонте событий то же самое должно быть и для x1.
Продолжая рассуждение, мы ожидаем, что управление u_i должно считаться как u_i = k_0 * x_i. То есть, оптимальное управление должно получаться скалярным произведением постоянного вектора k_0 и остаточного расстояния до цели x_i.
Но наш результат говорит ровно об обратном! Мы нашли, что u_i = k_i * x_0! То есть, мы нашли последовательность k_i, которая зависит только от структуры уравнения системы, но не от его состояния. И управление получается при помощи скалярного произведения постоянного вектора (начального положения системы) и найденной последовательности…
То есть, если всё хорошо, то у нас должно быть равенство k_0 * x_i = u_i = k_i * x_0. Давайте нарисуем иллюстративный график, взяв для простоты x_0 равным k_0. По одной оси графика отложим координату машины, по другой скорость. Начиная с одной точки k_0 = x_0 мы получим две разные последовательности точек k_i и x_i, сходящиеся к нулю координат.
Рисовалка доступна тут.
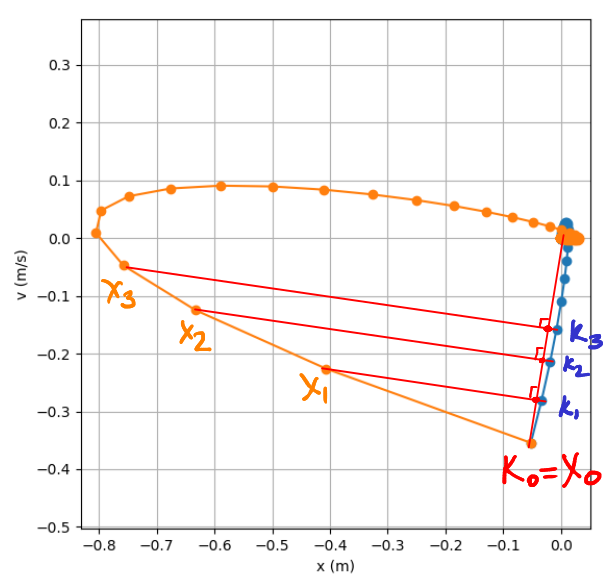
Если грубо, то k_i*x_0 образуют последовательность проекций k_i на вектор x_0. То же самое для k_0*x_i, это последовательность проекций x_i на k_0. На нашем графике хорошо видно, что эти проекции совпадают. Ещё раз, это не является доказательством, но лишь иллюстрацией.
Таким образом, мы получили динамическую систему вида x_{k+1} = (A+BK)x_k. Если собственные числа матрицы A+BK по модулю меньше единицы, то эта система сходится к началу координат при любых начальных x_0. Иначе говоря, решением этого дифференциального уравнения является (матричная) экспонента.
В сумасшедшем доме, куда привезены не выдержавшие нагрузки в сессию студенты-математики, один из них бегает с ножом и кричит: «Всех продифференцирую!». Пациенты разбегаются, кроме другого студента-математика. Когда первый врывается в палату с криком «Продифференцирую!», второй флегматично замечает: «Я е в степени икс!». Первый, помахивая ножом: «Продифференцирую по игрек!»
В качестве иллюстрации я случайно выбрал несколько сотен разных x_0, и нарисовал траектории нашей машинки. Рисовалку брать тут. Вот получившаяся картинка:
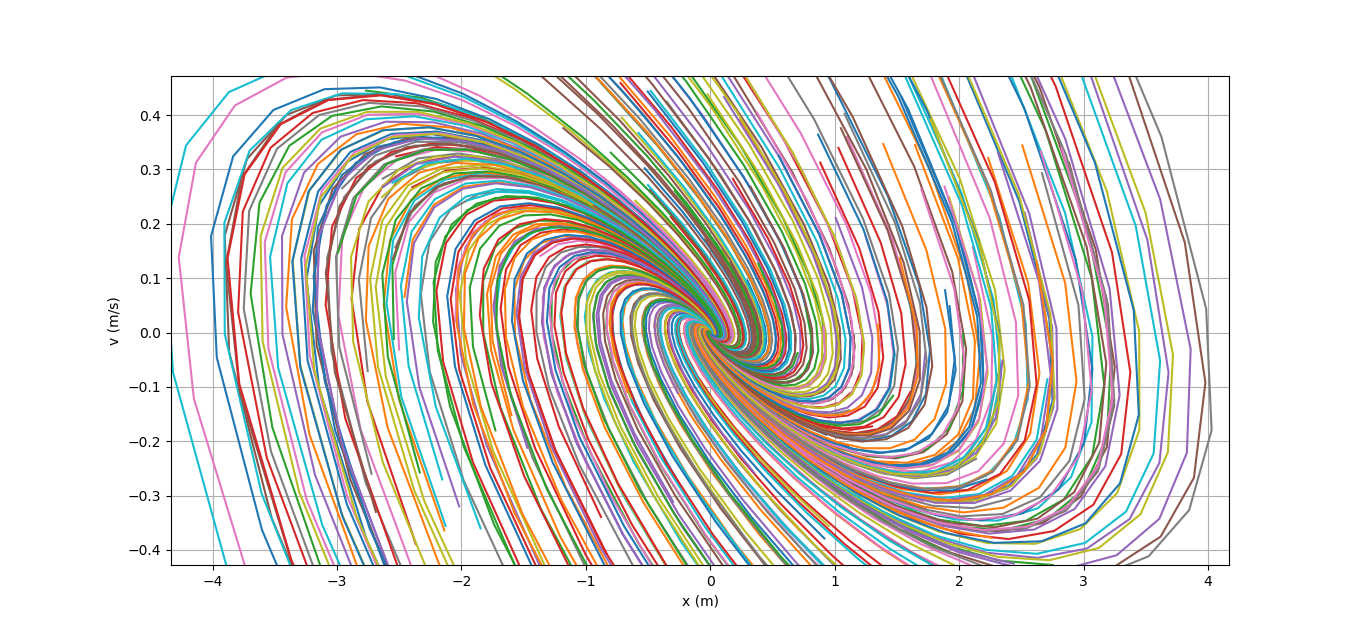
Все траектории благополучно сходятся к нулю, небольшое закручивание траекторий говорит о том, что матрица A+BK является матрицей поворота и стягивания (имеет комплексные собственные числа, по модулю меньшие единицы). Если не ошибаюсь, то эта картинка зовётся фазовым портретом.
Разомкнутый и замкнутый контуры управления
Итак, мы бодро минимизировали нашу функцию J, и получили оптимальный вектор управления U0 как K*X0:
U=K*X0
X=Abar*X0 + Bbar*U
Есть ли всё же разница между тем, чтобы считать управление так или как u_i = k_0 * x_i? Есть колоссальная, если у нас в системе есть неучтённые факторы (то есть, почти всегда). Давайте представим, что наш автомобиль катится не по горизонтальной поверхности, но у него на пути может встретиться вот такая горка:
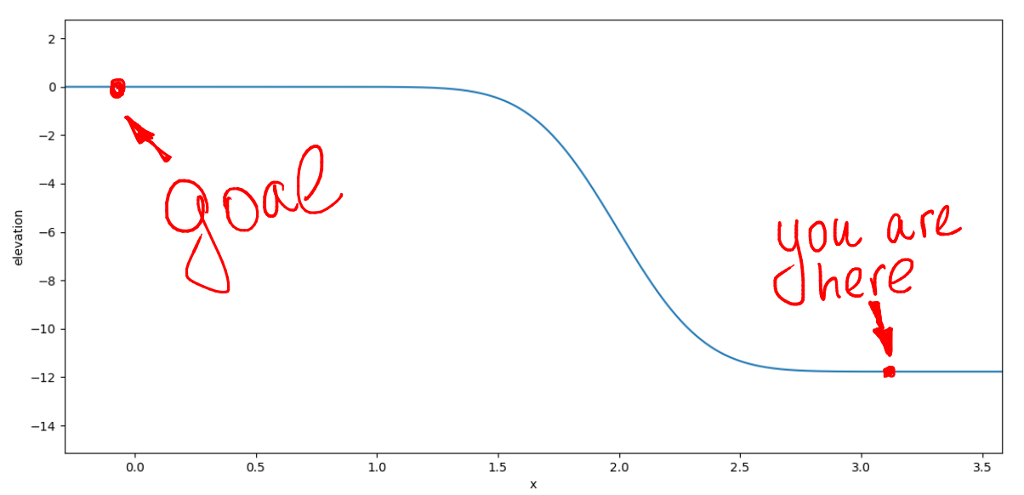
Если мы посчитаем оптимальное управление без учёта этой горки, то может случиться беда
(рисовалка тут):
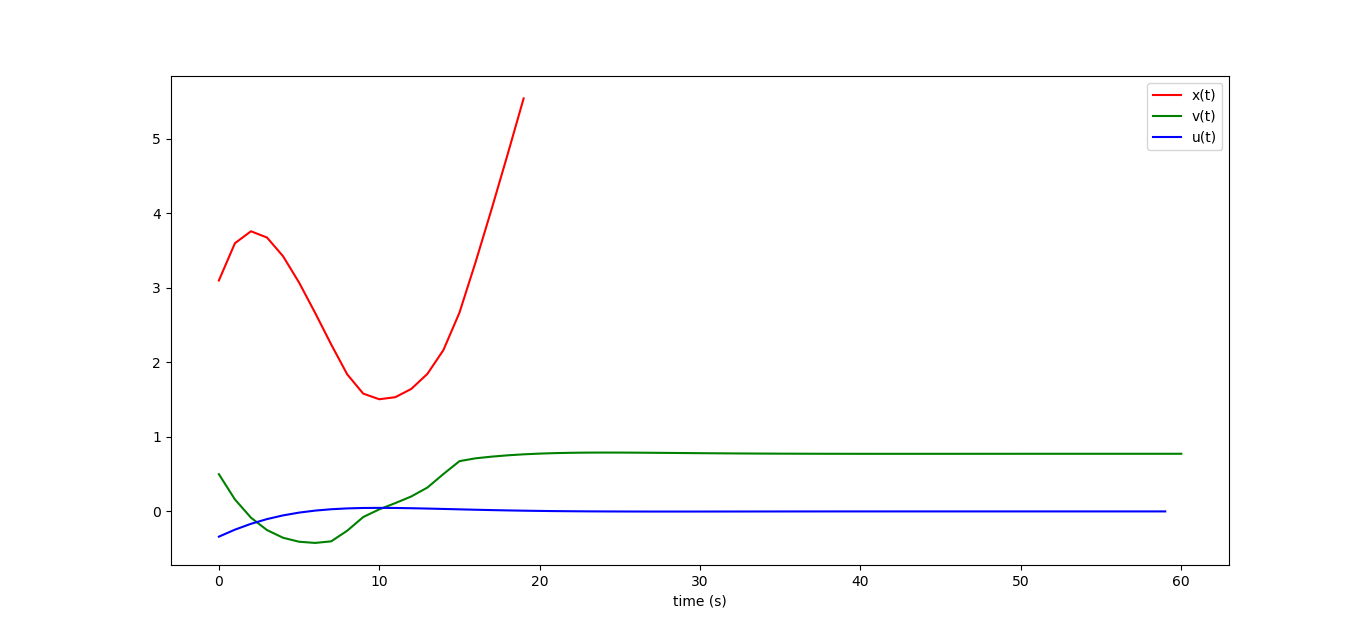
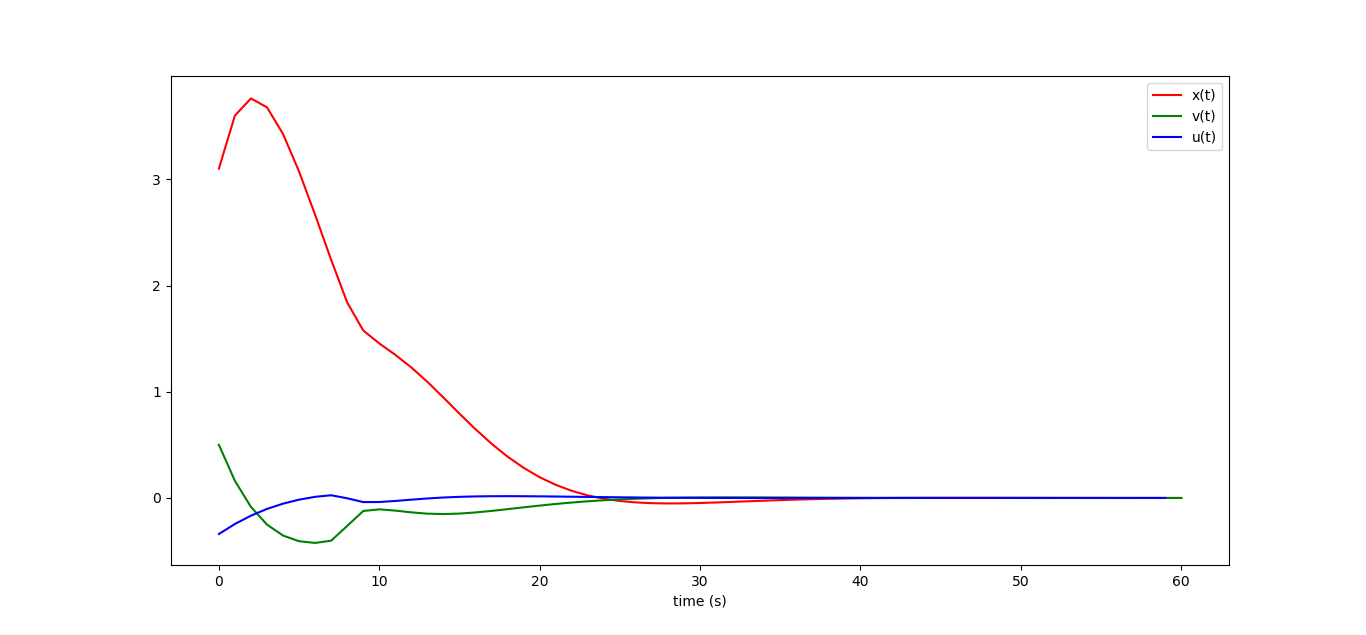
Машинка не только не остановится, но и вовсе уедет в бесконечность направо, я даже графика x_i нарисовал только одну треть, дальше оно линейно растёт. Если же мы замкнём контур управления, то небольшие возмущения динамики системы не приводят к катастрофическим последствиям:
for i in range(N):
Xi = X[i*n:(i+1)*n,0]
U[i*m:(i+1)*m,0] = K[0:m,:]*Xi
idxslope = int((Xi[0,0]+5)/10.*1000.)
if (idxslope<0 or idxslope>=1000):
idxslope = 0
X[(i+1)*n:(i+2)*n,0] = A*Xi + B*U[i*m:(i+1)*m,0] + B*slope[idxslope]
Построение линейного наблюдателя
Итак, мы умеем управлять динамической системой, чтобы она стремилась попасть в начало координат. Но что если мы хотели бы, чтобы автомобиль остановился не в x=0, но в x=3? Очевидно, что достаточно из текущего состояния x_i вычесть желаемый результат, и дальше всё как обычно. Причём этот желаемый результат вполне может не быть постоянным, но изменяться во времени. А можем ли мы следить за другой динамической системой?
Давайте предположим, что нашей машинкой мы не управляем напрямую, но при этом хотим за ней следить. Оба состояния машины мы измеряем при помощи каких-то датчиков, которые имеют довольно низкое разрешение:
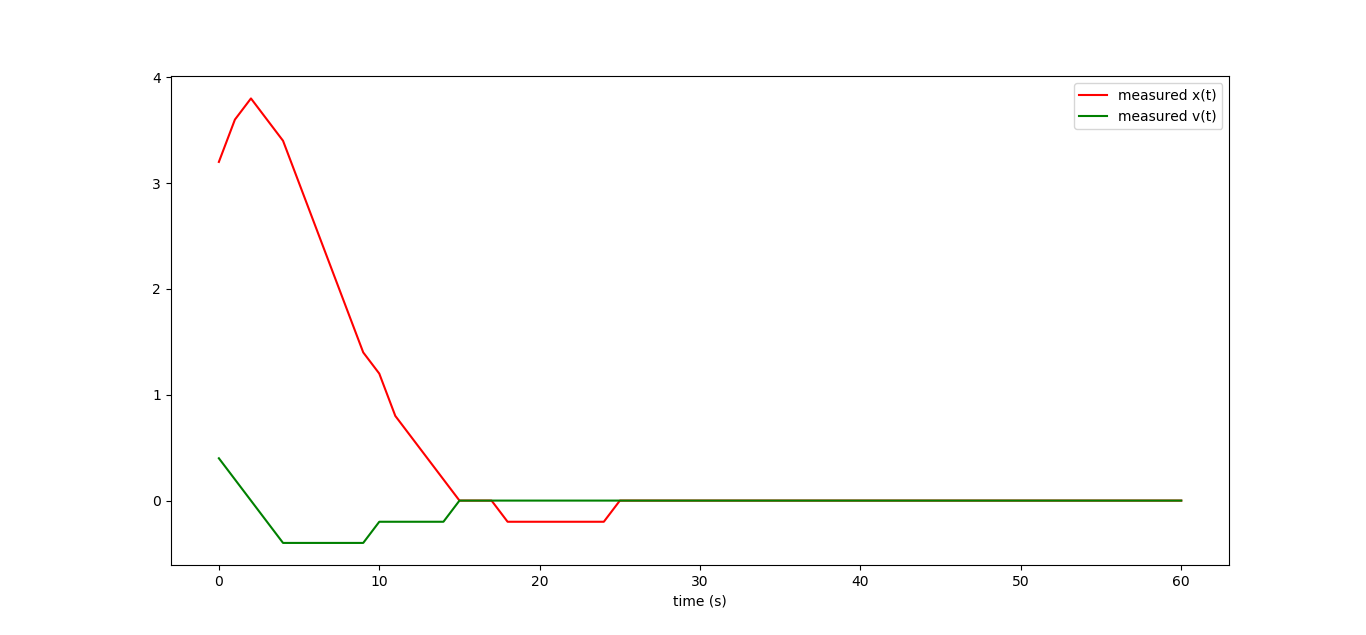
Я просто взял наши кривые и загрубил их значения. Давайте попробуем отфильтровать шум, внесённый измерениями. Как обычно, вооружаемся наименьшими квадратами.
Когда у тебя в руках молоток, всё вокруг кажется гвоздями.
Итак, наша машинка подчиняется закону x_{k+1} = A x_k + B u_k, поэтому давайте построим диффур-наблюдатель, который следует тому же закону:
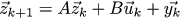
Здесь y_k — это корректирующий член, через который мы будем сообщать нашему наблюдателю, насколько мы далеко от реального положения вещей. Как и в прошлый раз, запишем уравнение в матричной форме:
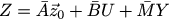
Окей. Теперь чего мы хотим? Мы хотим, чтобы корректирующие члены y_k были маленькими, и чтобы z_k сошёлся к x_k:
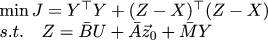
Как и в прошлый раз, выражаем Z через Y, приравниваем частные производные по Y нулю, и получаем выражение для оптимального корректирующего члена:
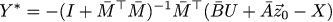
Тут меня начинают терзать смутные предчувствия… Где-то я это уже видел! Хорошо, давайте вспомним, как связаны X с U, получим следующее выражение:
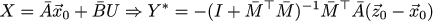
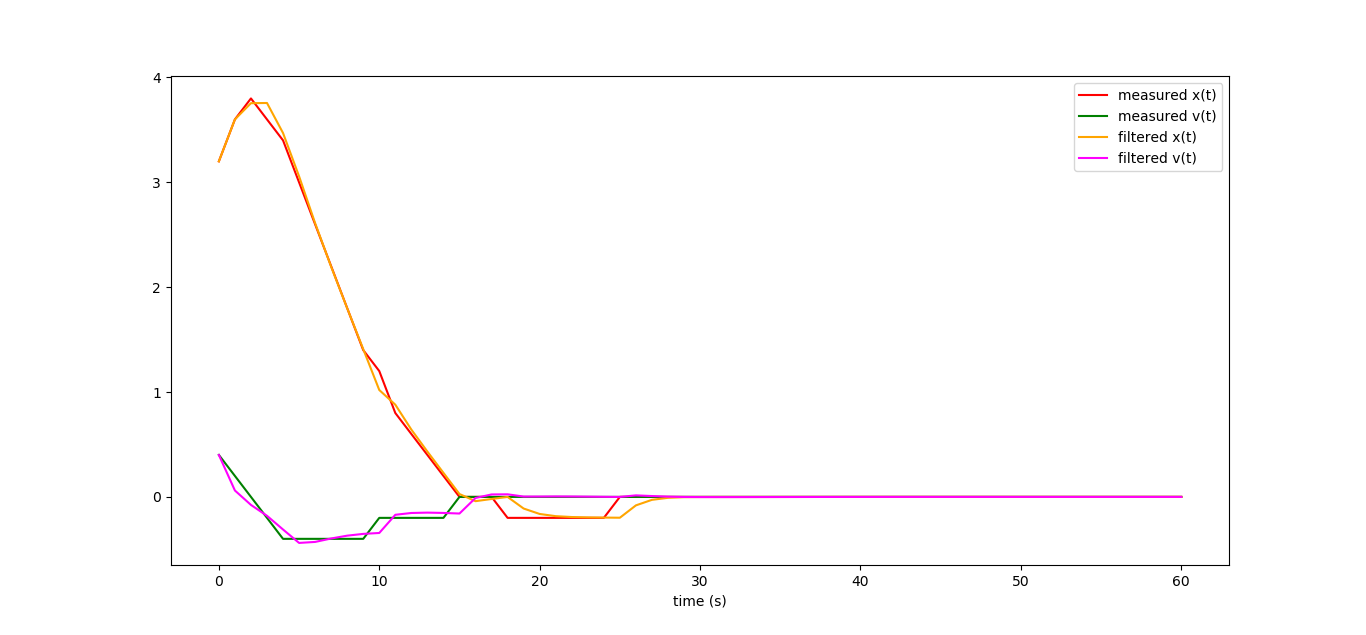
Но ведь это с точностью до переименования буковок выражение для U*! И в самом деле, давайте вернёмся чуть-чуть назад, слишком быстро мы ринулись в дело. Комбинируя динамику для x_k с динамикой для z_k мы получаем динамику для ошибки x_k-z_k.
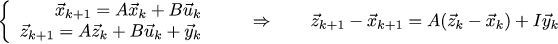
То есть, наша задача слежения за машинкой абсолютно эквивалентна задаче линейно-квадратичного регулятора. Находим оптимальную матрицу усиления, которая в нашем случае будет равна [[-0.594,-0.673],[-0.079,-0.774]], и получаем следующий код наблюдателя:
for i in range(N):
Zi = Z[i*n:(i+1)*n,0]
Xi = X[i*n:(i+1)*n,0]
Z[(i+1)*n:(i+2)*n,0] = A*Zi + B*U[i*m:(i+1)*m,0] + np.matrix([[-0.594,-0.673],[-0.079,-0.774]])*(Zi-Xi)
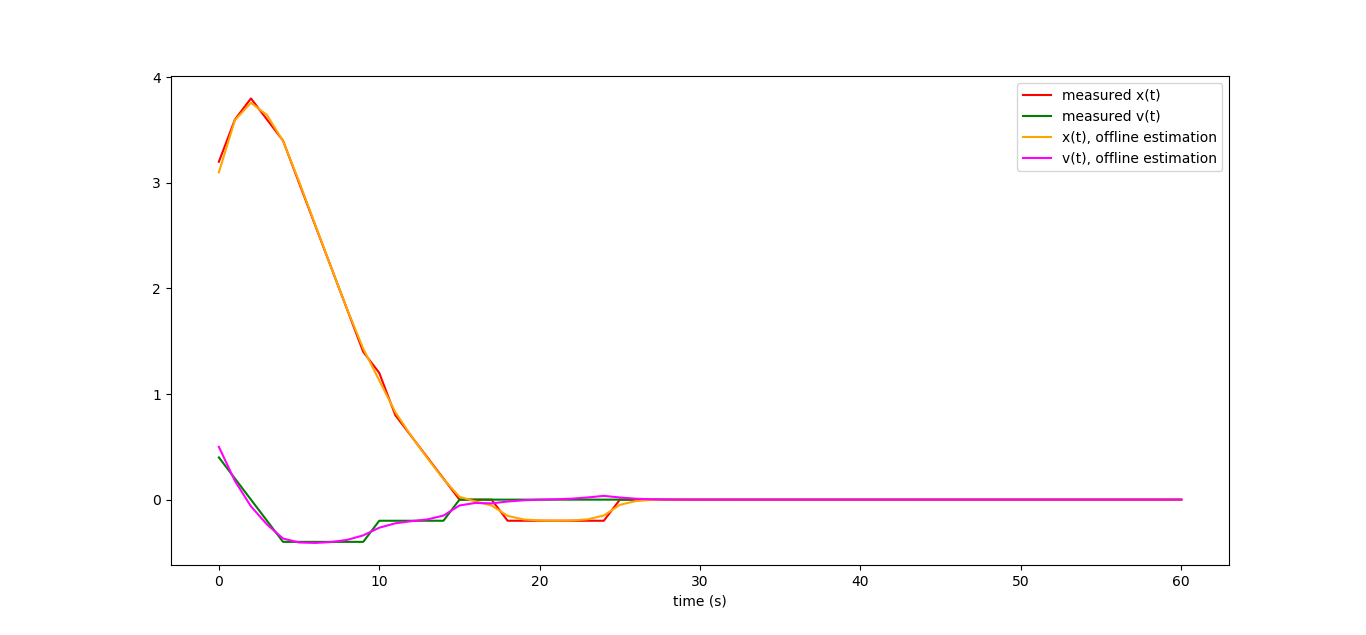
А вот отфильтрованные кривые, они неидеальны, но всё же ближе к реальности, нежели измерения с низким разрешением.
Динамика системы определяется собственными числами матрицы [[1–0.594,1–0.673],[-0.079,1–0.774]], которые равны (0.316 ± 0.133 i).
А давайте пойдём ещё дальше. Давайте предположим, что измерять мы можем только положение, а для скорости датчика нет. Сумеем ли мы построить наблюдатель в этом случае? Тут мы выходим за рамки LQR, но не слишком далеко. Давайте запишем следующую систему:
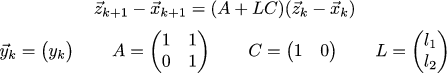
Матрица C нам предписывает то, что мы реально можем наблюдать в нашей системе. Наша задача найти такую матрицу L, которая позволит наблюдателю себя хорошо вести. Давайте руками предпишем, что собственные числа матрицы A+LC, которая описывает общую динамику наблюдателя, должны быть примерно такими же, как и собственные числа матрицы из предыдущего примера. Давайте приблизим предыдущие собственные числа дробями (⅓ ± 1/6 i). Запишем характеристический многочлен матрицы A+LC, и заставим его быть равным многочлену (x-(⅓+1/6*i))*(x-(⅓–1/6*i). Затем решаем простейшую систему из линейных уравнений, и матрица L найдена.
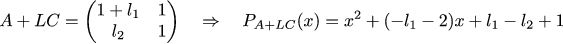
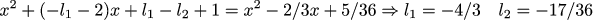
Вычисления можно проверить тут, а рисовалку графиков брать тут.
Вот так выглядят графики работы нашего наблюдателя, если мы измеряем (причём с большой погрешностью) только координату нашей машинки:
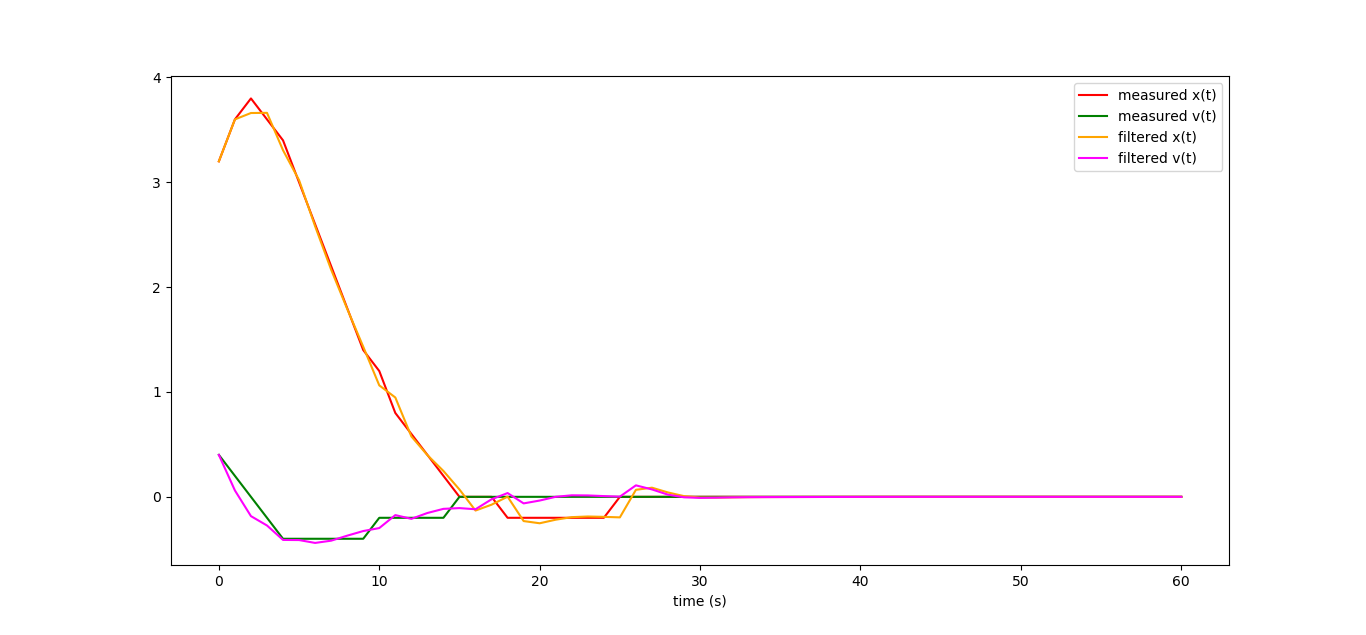
Из очень неполных данных мы весьма неплохо можем восстановить динамику всей системы! К слову, построенный нами линейный наблюдатель по факту является знаменитым фильтром Калмана, но про это будем разговаривать как-нибудь в следующий раз.
Вопрос для внимательных читателей
Если всё же довести до логического конца вычисления Y* (код брать тут), то итоговые кривые наблюдателя гораздо, гораздо более гладкие (и ближе к правде!) нежели те, что должны быть им эквивалентны. Почему?