Исследователи смогли преодолеть барьер в улучшении решения задачи коммивояжера

Натан Кляйн и его советники из Вашингтонского университета Анна Карлин и Шаян Гаран впервые за почти полвека смогли найти лучший способ решения задачи коммивояжера. Это одна из самых известных задач комбинаторной оптимизации, заключающаяся в поиске самого выгодного маршрута через указанные города с последующим возвратом в исходный город.
На протяжении десятилетий задача вдохновила на многие из фундаментальных достижений в области информатики, в частности, в сфере линейного программирования. В 1976 году Никос Кристофидес придумал алгоритм, который эффективно находит приблизительные решения задачи. Однако впоследствии ни у кого не получилось улучшить этот алгоритм.
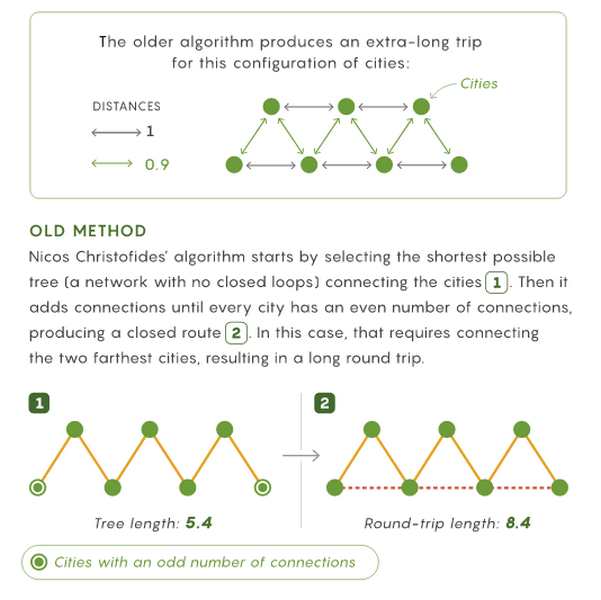
В алгоритме Кристофидеса все начинается с остовного дерева, соединяющего города без замкнутых петель. Чтобы построить его, нужно начать с поиска кратчайшего пути между двумя городами. Для каждой следующей ветви нужно найти кратчайший путь между новым городом и одним из двух предыдущих.
Результирующее дерево позволяет пройти маршрут через каждый город и вернуться назад, но обычно длина такого пути далека от кратчайшей. Тем не менее, полученный путь в худшем случае не превышает кратчайший более чем на 50%.
В 2010 году Амин Сабери из Стэнфордского университета, аспиранты Араш Асадпур, Шайан Гаран и Александер Мадри, а также Майкл Гоманс из МТИ показали новый алгоритм, который начинает с подсчёта точного дробного решения задачи коммивояжёра, а затем округляет это решение до остовного дерева. Наконец, алгоритм включает это дерево в сеть Кристофидеса.
Таким образом, исследователи смогли улучшить алгоритм Кристофидеса на небольшую долю для широкого подкласса «графических» задач коммивояжера.
Теперь Гаран и другие вернулись к задаче. Они решили использовать геометрию многочленов, составленных из чисел и переменных в степенях, например 3×2y + 8xz7. Чтобы изучить проблему коммивояжера, исследователи преобразовали карту городов в полином, в котором было по одной переменной для каждого ребра между городами и по одному члену для каждого дерева, которое могло соединить все города.
Они обнаружили, что этот многочлен обладает так называемой «реальной стабильностью». Поэтому, если исследователи хотят сосредоточиться на определенных городах, они могут использовать одну переменную для представления различных ребер, ведущих в город, а для ребер, которые им не важны, установить величину, равную 1.
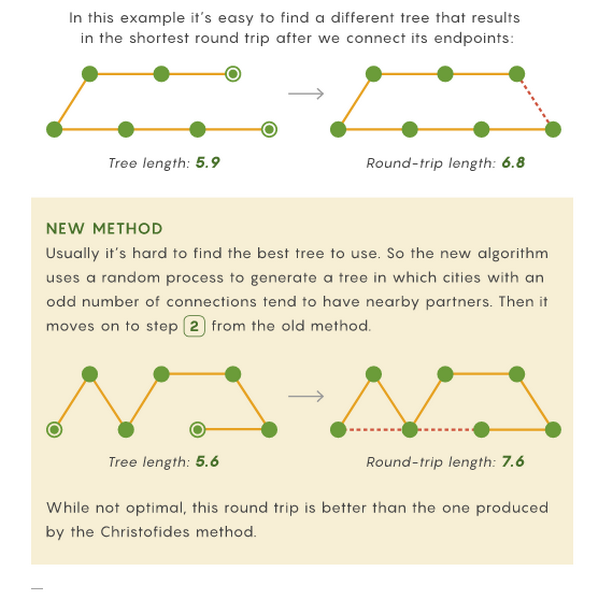
Такой подход позволил исследователям выяснить, например, как часто алгоритм будет вынужден соединять два удаленных города. Им удалось показать, что этот алгоритм превосходит исходник Кристофидеса для решения общей задачи коммивояжера.
Пока улучшения алгоритма оцениваются в доли процента, но, как показывает практика, это может быть очередным прорывом в решении задачи коммивояжера. После разработки алгоритма Сабери и других результат решения уже улучшился с 50 до 40%.
См. также:
